课题学习镶嵌
图片预览









文档简介
(共35张PPT)
人教版义务教育课程标准实验教科书七年级下册
好漂亮的地板!这是怎么铺设的 一点空隙也没有.
我们经常能见到各种建筑物的地板,观察地板,就能发现地板常用各种多边形地砖铺砌成美丽的图案。
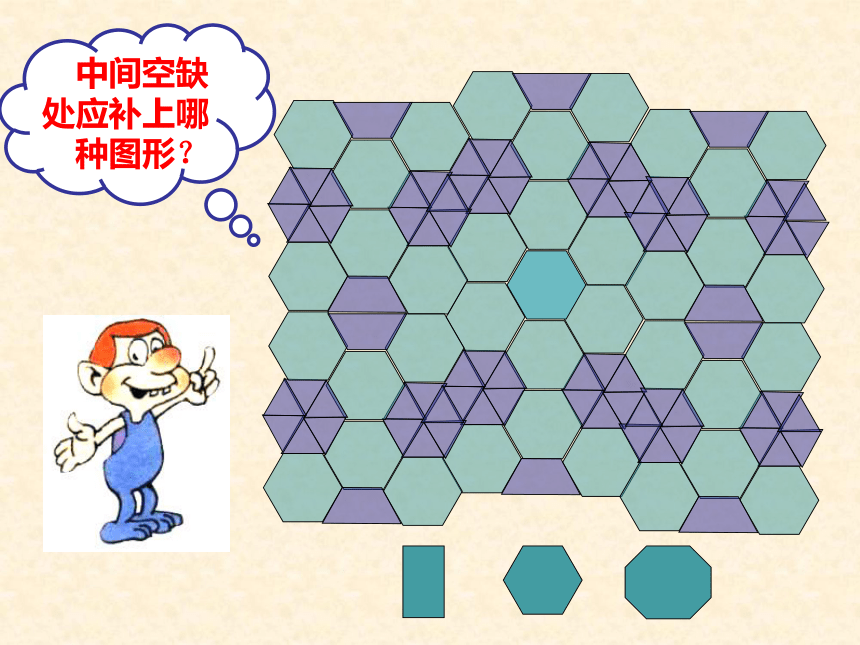
中间空缺处应补上哪种图形?
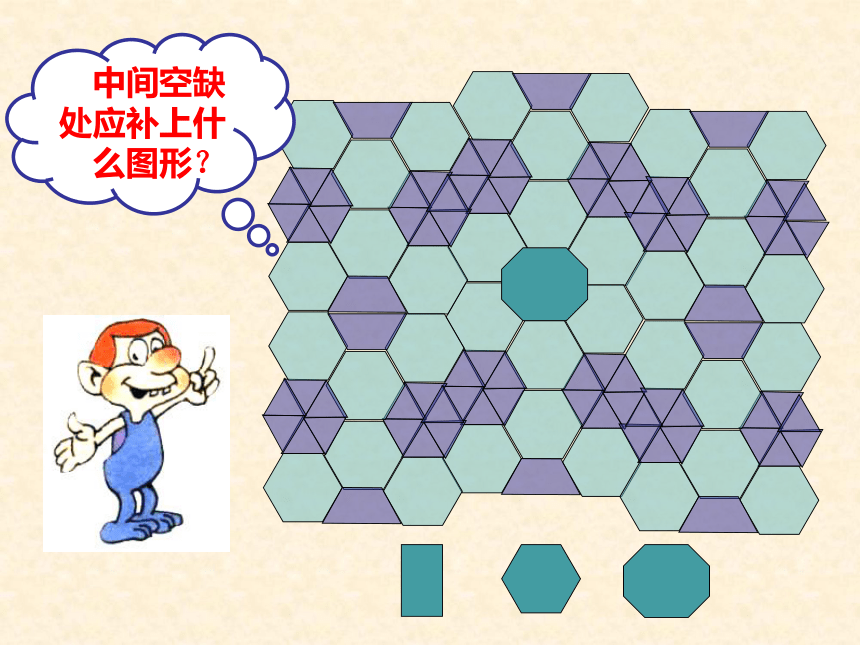
中间空缺处应补上什么图形?
中间空缺处应补上什么图形?
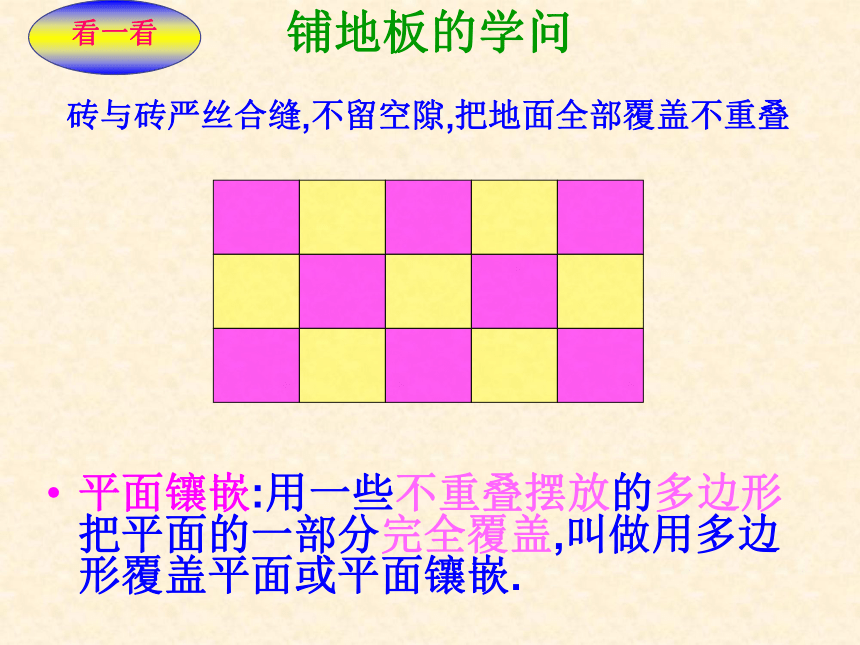
铺地板的学问
平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面或平面镶嵌.
看一看
砖与砖严丝合缝,不留空隙,把地面全部覆盖不重叠
探究1:仅用一种正多边形镶嵌,哪些正多边形能单独镶嵌成一个平面图案?
正方形
正三角形
正六边形
做一做:
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
用边长相同的正五边形能否镶嵌?
探究2:用边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案?
60°×3+90°×2=360°
60°×4 + 120°=360°
60°×2+120°×2=360°
正方形和正六边形不能镶嵌
讨 论
正三角形和正方形能镶嵌
正方形和正六边形能镶嵌
想一想
正方形和正八边形能否镶嵌
正三角形和正十二边形能否镶嵌
135°
135°
90°
150°
150°
60°
正八边形和正方形
正十二边形和正三角形
探究3:
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢?
1
3
2
1
4
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
任意三角形能镶嵌成平面图案。
因为∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
所以任意四边形能镶嵌成平面图案。
多边形镶嵌的条件:
拼接在同一个顶点处的各个多边形的内角之和等于360°
谈一谈:
通过本课的学习有哪些收获
和体会?
问题情景
我们学校正在兴建的食堂地上
想用两种或两种以上的正多边
形的地砖来镶嵌,现正向大家
征集方案,小组合作设计几个吧?
设计一下
希望同学们:
关注身边的数学
关注数学中的美
人教版义务教育课程标准实验教科书七年级下册
好漂亮的地板!这是怎么铺设的 一点空隙也没有.
我们经常能见到各种建筑物的地板,观察地板,就能发现地板常用各种多边形地砖铺砌成美丽的图案。
中间空缺处应补上哪种图形?
中间空缺处应补上什么图形?
中间空缺处应补上什么图形?
铺地板的学问
平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面或平面镶嵌.
看一看
砖与砖严丝合缝,不留空隙,把地面全部覆盖不重叠
探究1:仅用一种正多边形镶嵌,哪些正多边形能单独镶嵌成一个平面图案?
正方形
正三角形
正六边形
做一做:
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
用边长相同的正五边形能否镶嵌?
探究2:用边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案?
60°×3+90°×2=360°
60°×4 + 120°=360°
60°×2+120°×2=360°
正方形和正六边形不能镶嵌
讨 论
正三角形和正方形能镶嵌
正方形和正六边形能镶嵌
想一想
正方形和正八边形能否镶嵌
正三角形和正十二边形能否镶嵌
135°
135°
90°
150°
150°
60°
正八边形和正方形
正十二边形和正三角形
探究3:
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢?
1
3
2
1
4
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
任意三角形能镶嵌成平面图案。
因为∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
所以任意四边形能镶嵌成平面图案。
多边形镶嵌的条件:
拼接在同一个顶点处的各个多边形的内角之和等于360°
谈一谈:
通过本课的学习有哪些收获
和体会?
问题情景
我们学校正在兴建的食堂地上
想用两种或两种以上的正多边
形的地砖来镶嵌,现正向大家
征集方案,小组合作设计几个吧?
设计一下
希望同学们:
关注身边的数学
关注数学中的美
