2020-2021学年人教版八年级下册数学18.1.1平行四边形的性质 同步练习(word版,含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学18.1.1平行四边形的性质 同步练习(word版,含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 280.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 00:00:00 | ||
图片预览


文档简介
18.1.1平行四边形的性质
同步练习
一、单选题
1.已知平行四边形的一边长为5,则对角线,的长可取下列数据中的(
)
A.2和4
B.3和4
C.4和5
D.5和6
2.如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是(
)
A.60
B.30
C.20
D.16
3.如图,在平行四边形中,是的中点,,,,则的长为(
)
A.
B.
C.
D.
4.已知平行四边形中,,E是上一点,的周长是平行四边形周长的一半,且,连结,则的长为(
)
A.2
B.3
C.4
D.5
5.如图,在平行四边形中,,,对角线与相交于点,点是的中点,连接交于点.若,则的长为(
)
A.
B.
C.
D.
6.如图,过平行四边形对角线的交点O,交于点E,交于点F,若平行四边形的周长为36,,则四边形的周长为(
)
A.28
B.26
C.24
D.20
7.如图,P为□ABCD对角线BD上一点,△ABP的面积为S1,△CBP的面积为S2,则S1和S2的关系为
(
)
A.S1>S2
B.S1=S2
C.S1D.无法判断
8.如图,平行四边形ABCD的对角线AC、BD相交于O,EF过点O与AD、BC分别相交于E、F.若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为(
)
A.16
B.14
C.10
D.12
9.如图,中,点在边上,以为折痕,将向上翻折,点正好落在上的点处,若的周长为,的周长为,则的长为(
)
A.
B.
C.
D.
10.如图,平行四边形的对角线与相交于点,于点,,,
,则的长为(
)
A.
B.
C.
D.
二、填空题
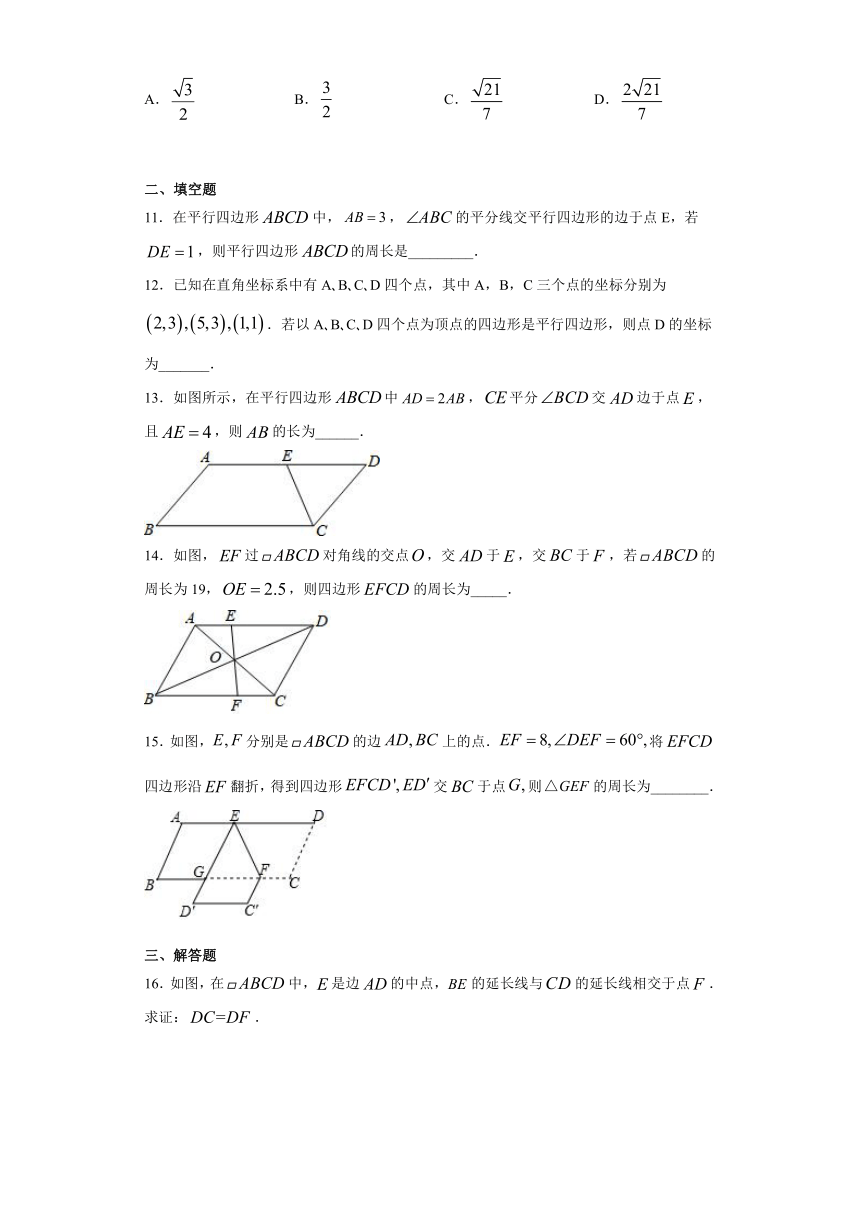
11.在平行四边形中,,的平分线交平行四边形的边于点E,若,则平行四边形的周长是_________.
12.已知在直角坐标系中有A?B?C?D四个点,其中A,B,C三个点的坐标分别为.若以A?B?C?D四个点为顶点的四边形是平行四边形,则点D的坐标为_______.
13.如图所示,在平行四边形中,平分交边于点,且,则的长为______.
14.如图,过对角线的交点,交于,交于,若的周长为19,,则四边形的周长为_____.
15.如图,分别是的边上的点.将四边形沿翻折,得到四边形交于点则的周长为________.
三、解答题
16.如图,在中,是边的中点,的延长线与的延长线相交于点.
求证:.
17.如图,中,、是直线上两点,且.
求证:(1);
(2).
18.如图,在中,?分别是和的角平分线,已知.
(1)求线段的长;
(2)延长,交的延长线于点Q.
①请在答卷上补全图形;
②若,求的周长.
参考答案
1.D
2.C
3.D
4.B
5.C
6.C
7.B
8.D
9.C
10.D
11.14
12.(4,1)或(6,5)或(-2,1)
13.4
14.14.5
15.24
16.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=DC,
∴∠F=∠EBA,
∵E是AD边的中点,
∴DE=AE,
在△DEF和△AEB中,
,
∴△DEF≌△AEB(AAS),
∴DF=AB,
∴DC=DF.
17.证明:(1)四边形是平行四边形,
,
,
,
,
,
在和中,
,
,
;
(2),
,
.
18.解:(1)∵在□ABCD中,AD=5,
∴BC=5,
∵AB∥CD,
∴∠BAP=∠DPA,
∵AP平分∠BAD,
∴∠BAP=∠DAP,
∴∠DAP=∠DPA,
∴DP=AD=5,
同理可得,CP=BC=5,
∴CD=10,
∴AB=10;
(2)①如图所示:
②∵AD∥BQ,
∴∠Q=∠DAP,
又∵∠DAP=∠BAP,
∴∠Q=∠BAP,
∴AB=QB=10,
又∵BP平分∠ABQ,
∴BP⊥AQ,AP=QP,
∴Rt△ABP中,AP==8,
∴AQ=16,
∴△ABQ的周长为:16+10+10=36.
同步练习
一、单选题
1.已知平行四边形的一边长为5,则对角线,的长可取下列数据中的(
)
A.2和4
B.3和4
C.4和5
D.5和6
2.如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是(
)
A.60
B.30
C.20
D.16
3.如图,在平行四边形中,是的中点,,,,则的长为(
)
A.
B.
C.
D.
4.已知平行四边形中,,E是上一点,的周长是平行四边形周长的一半,且,连结,则的长为(
)
A.2
B.3
C.4
D.5
5.如图,在平行四边形中,,,对角线与相交于点,点是的中点,连接交于点.若,则的长为(
)
A.
B.
C.
D.
6.如图,过平行四边形对角线的交点O,交于点E,交于点F,若平行四边形的周长为36,,则四边形的周长为(
)
A.28
B.26
C.24
D.20
7.如图,P为□ABCD对角线BD上一点,△ABP的面积为S1,△CBP的面积为S2,则S1和S2的关系为
(
)
A.S1>S2
B.S1=S2
C.S1
8.如图,平行四边形ABCD的对角线AC、BD相交于O,EF过点O与AD、BC分别相交于E、F.若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为(
)
A.16
B.14
C.10
D.12
9.如图,中,点在边上,以为折痕,将向上翻折,点正好落在上的点处,若的周长为,的周长为,则的长为(
)
A.
B.
C.
D.
10.如图,平行四边形的对角线与相交于点,于点,,,
,则的长为(
)
A.
B.
C.
D.
二、填空题
11.在平行四边形中,,的平分线交平行四边形的边于点E,若,则平行四边形的周长是_________.
12.已知在直角坐标系中有A?B?C?D四个点,其中A,B,C三个点的坐标分别为.若以A?B?C?D四个点为顶点的四边形是平行四边形,则点D的坐标为_______.
13.如图所示,在平行四边形中,平分交边于点,且,则的长为______.
14.如图,过对角线的交点,交于,交于,若的周长为19,,则四边形的周长为_____.
15.如图,分别是的边上的点.将四边形沿翻折,得到四边形交于点则的周长为________.
三、解答题
16.如图,在中,是边的中点,的延长线与的延长线相交于点.
求证:.
17.如图,中,、是直线上两点,且.
求证:(1);
(2).
18.如图,在中,?分别是和的角平分线,已知.
(1)求线段的长;
(2)延长,交的延长线于点Q.
①请在答卷上补全图形;
②若,求的周长.
参考答案
1.D
2.C
3.D
4.B
5.C
6.C
7.B
8.D
9.C
10.D
11.14
12.(4,1)或(6,5)或(-2,1)
13.4
14.14.5
15.24
16.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=DC,
∴∠F=∠EBA,
∵E是AD边的中点,
∴DE=AE,
在△DEF和△AEB中,
,
∴△DEF≌△AEB(AAS),
∴DF=AB,
∴DC=DF.
17.证明:(1)四边形是平行四边形,
,
,
,
,
,
在和中,
,
,
;
(2),
,
.
18.解:(1)∵在□ABCD中,AD=5,
∴BC=5,
∵AB∥CD,
∴∠BAP=∠DPA,
∵AP平分∠BAD,
∴∠BAP=∠DAP,
∴∠DAP=∠DPA,
∴DP=AD=5,
同理可得,CP=BC=5,
∴CD=10,
∴AB=10;
(2)①如图所示:
②∵AD∥BQ,
∴∠Q=∠DAP,
又∵∠DAP=∠BAP,
∴∠Q=∠BAP,
∴AB=QB=10,
又∵BP平分∠ABQ,
∴BP⊥AQ,AP=QP,
∴Rt△ABP中,AP==8,
∴AQ=16,
∴△ABQ的周长为:16+10+10=36.
