2020-2021学年人教版八年级下册数学 18.1.2平行四边形的判定 同步练习(word版,含答案)
文档属性
| 名称 | 2020-2021学年人教版八年级下册数学 18.1.2平行四边形的判定 同步练习(word版,含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 379.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 08:27:54 | ||
图片预览


文档简介
18.1.2平行四边形的判定
同步练习
一、单选题
1.下列条件中不能判定一定是平行四边形的有( )
A.一组对角相等,一组邻角互补
B.一组对边平行,另一组对边相等
C.两组对边相等
D.一组对边平行,且另一组对边也平行
2.四边形中,对角线交于点.给出下列四组条件:
①∥,∥;
②,;
③,;
④∥,.
其中一定能判定这个四边形是平行四边形的条件共有(
)
A.1组;
B.2组;
C.3组;
D.4组.
3.如图,点D和点E分别是BC和BA的中点,已知AC=4,则DE为( )
A.1
B.2
C.4
D.8
4.如图,D,E,F分别是的中点,则:S梯形BCED是(
)
A.
B.
C.
D.
5.如图,在中,D,F分别是,上的点,且.点E是射线上一点,若再添加下列其中一个条件后,不能判定四边形为平行四边形的是(
)
A.
B.
C.
D.
6.如图,在中,,点分别是边上的动点,连接,点分别为的中点,连接,则的最小值为(
).
A.
B.
C.
D.1
7.如图,是的中线,分别是的中点,则等于(
)
A.
B.
C.
D.
8.如图,在中,,,平分,于点D,若点为的中点,连接,则的长是(
).
A.1
B.1.5
C.4
D.2
9.如图,中,点是的中点,,,则长(
).
A.7
B.8
C.9
D.10
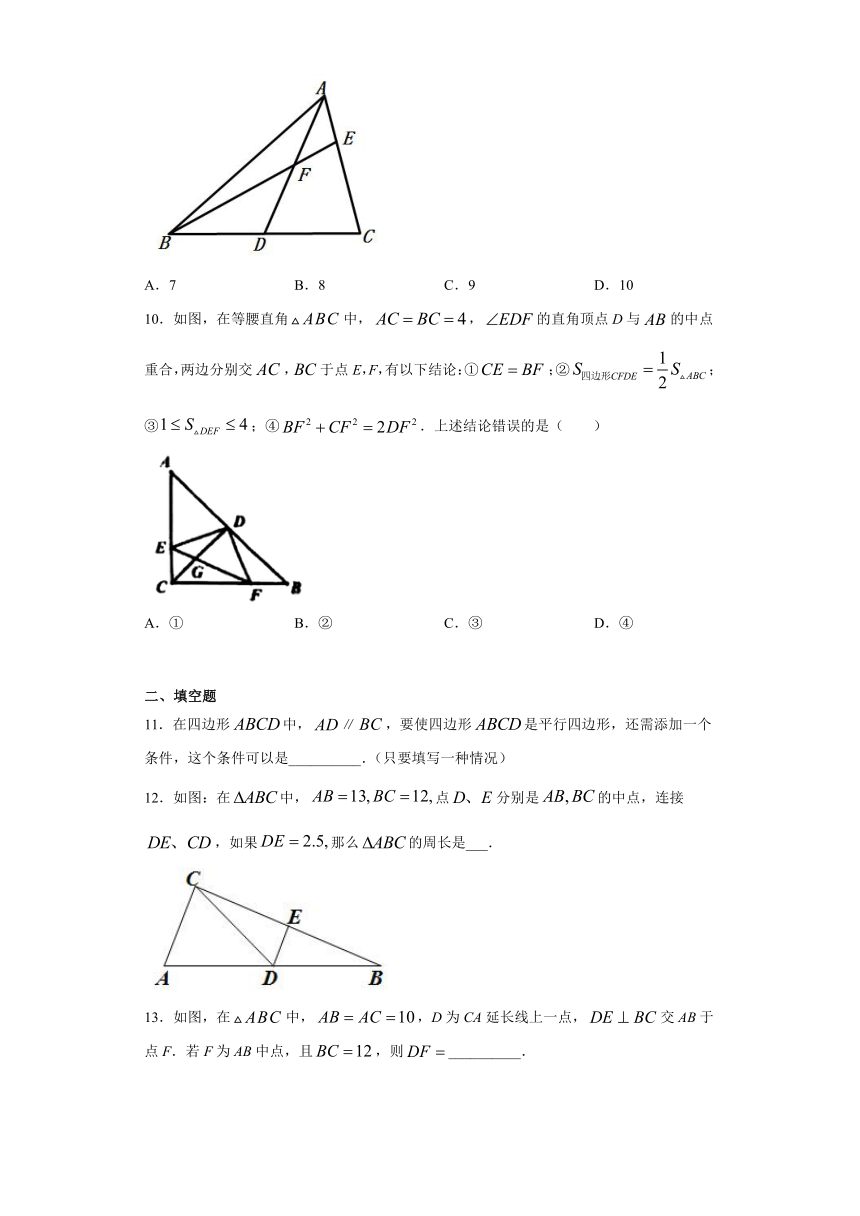
10.如图,在等腰直角中,,的直角顶点D与的中点重合,两边分别交,于点E,F,有以下结论:①;②;③;④.上述结论错误的是(
)
A.①
B.②
C.③
D.④
二、填空题
11.在四边形中,∥,要使四边形是平行四边形,还需添加一个条件,这个条件可以是__________.(只要填写一种情况)
12.如图:在中,点分别是的中点,连接,如果那么的周长是___.
13.如图,在中,,D为CA延长线上一点,交AB于点F.若F为AB中点,且,则__________.
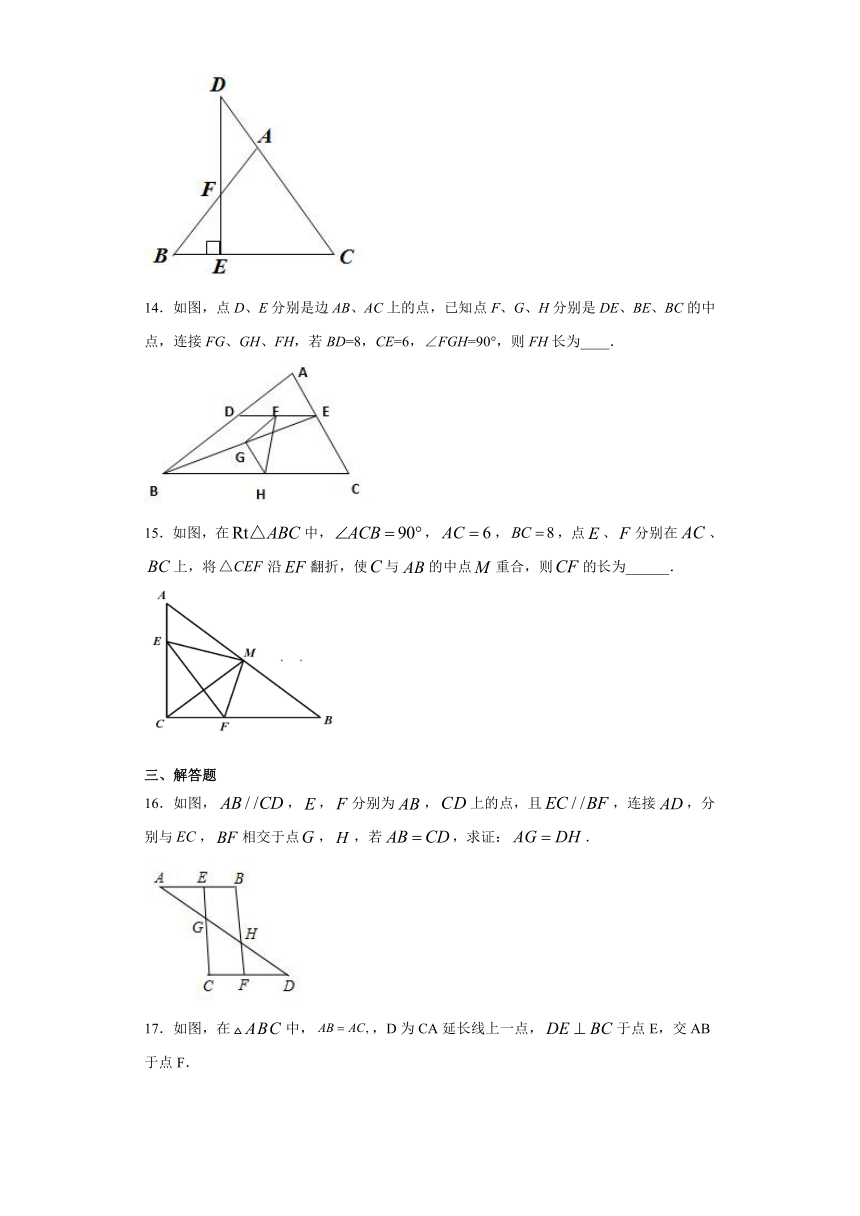
14.如图,点D、E分别是边AB、AC上的点,已知点F、G、H分别是DE、BE、BC的中点,连接FG、GH、FH,若BD=8,CE=6,∠FGH=90°,则FH长为____.
15.如图,在中,,,,点、分别在、上,将沿翻折,使与的中点重合,则的长为______.
三、解答题
16.如图,,,分别为,上的点,且,连接,分别与,相交于点,,若,求证:.
17.如图,在中,,D为CA延长线上一点,于点E,交AB于点F.
(1)求证:是等腰三角形;
(2)若,,求线段DE的长.
18.如图所示,在中,对角线,相交于点O,,E,F为直线上的两个动点(点E,F始终在的外面),且,连结,,,.
(1)求证:四边形为平行四边形.
(2)若,上述结论还成立吗?若呢?
(3)若平分,,求四边形的周长.
参考答案
1.B
2.C3.B
4.B
5.D
6.A
7.B
8.D
9.C
10.C
11.(答案不唯一)
12.30
13.8
14.5
15.
16.证明:∵,,
∴四边形是平行四边形,,
∴,,
∴.
∵,∴.
∵在和中,
,
∴,
∴.
17.解:(1)∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠C+∠D=90°,∠B+∠BFE=90°,
∴∠D=∠BFE,
又∵∠BFE=∠AFD,
∴∠D=∠AFD,
∴AD=AF,即△ADF为等腰三角形;
(2)过A作AH⊥BC,
∵,DE⊥BC,
∴EF//AH,
∴EF是△BAH的中位线,
∵BE=2,
∴EH=2,
∵AB=AC,
∴BC=4BE=8,EC=HC+HE=BH+EH=6,
∵DA=AF=5,AC=AB=10,
∴DC=AD+AC=15,
∴.
18.解:(1)证明:四边形是平行四边形,
,.
,,
,
,
四边形为平行四边形.
(2),,
,
,
四边形为平行四边形.
上述结论成立,
由此可得出结论:若,,则四边形为平行四边形.
(3)在中,,
.
平分,
,
,
.
,
,
是的垂直平分线,
.
,
是等边三角形,
,
.
同步练习
一、单选题
1.下列条件中不能判定一定是平行四边形的有( )
A.一组对角相等,一组邻角互补
B.一组对边平行,另一组对边相等
C.两组对边相等
D.一组对边平行,且另一组对边也平行
2.四边形中,对角线交于点.给出下列四组条件:
①∥,∥;
②,;
③,;
④∥,.
其中一定能判定这个四边形是平行四边形的条件共有(
)
A.1组;
B.2组;
C.3组;
D.4组.
3.如图,点D和点E分别是BC和BA的中点,已知AC=4,则DE为( )
A.1
B.2
C.4
D.8
4.如图,D,E,F分别是的中点,则:S梯形BCED是(
)
A.
B.
C.
D.
5.如图,在中,D,F分别是,上的点,且.点E是射线上一点,若再添加下列其中一个条件后,不能判定四边形为平行四边形的是(
)
A.
B.
C.
D.
6.如图,在中,,点分别是边上的动点,连接,点分别为的中点,连接,则的最小值为(
).
A.
B.
C.
D.1
7.如图,是的中线,分别是的中点,则等于(
)
A.
B.
C.
D.
8.如图,在中,,,平分,于点D,若点为的中点,连接,则的长是(
).
A.1
B.1.5
C.4
D.2
9.如图,中,点是的中点,,,则长(
).
A.7
B.8
C.9
D.10
10.如图,在等腰直角中,,的直角顶点D与的中点重合,两边分别交,于点E,F,有以下结论:①;②;③;④.上述结论错误的是(
)
A.①
B.②
C.③
D.④
二、填空题
11.在四边形中,∥,要使四边形是平行四边形,还需添加一个条件,这个条件可以是__________.(只要填写一种情况)
12.如图:在中,点分别是的中点,连接,如果那么的周长是___.
13.如图,在中,,D为CA延长线上一点,交AB于点F.若F为AB中点,且,则__________.
14.如图,点D、E分别是边AB、AC上的点,已知点F、G、H分别是DE、BE、BC的中点,连接FG、GH、FH,若BD=8,CE=6,∠FGH=90°,则FH长为____.
15.如图,在中,,,,点、分别在、上,将沿翻折,使与的中点重合,则的长为______.
三、解答题
16.如图,,,分别为,上的点,且,连接,分别与,相交于点,,若,求证:.
17.如图,在中,,D为CA延长线上一点,于点E,交AB于点F.
(1)求证:是等腰三角形;
(2)若,,求线段DE的长.
18.如图所示,在中,对角线,相交于点O,,E,F为直线上的两个动点(点E,F始终在的外面),且,连结,,,.
(1)求证:四边形为平行四边形.
(2)若,上述结论还成立吗?若呢?
(3)若平分,,求四边形的周长.
参考答案
1.B
2.C3.B
4.B
5.D
6.A
7.B
8.D
9.C
10.C
11.(答案不唯一)
12.30
13.8
14.5
15.
16.证明:∵,,
∴四边形是平行四边形,,
∴,,
∴.
∵,∴.
∵在和中,
,
∴,
∴.
17.解:(1)∵AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠C+∠D=90°,∠B+∠BFE=90°,
∴∠D=∠BFE,
又∵∠BFE=∠AFD,
∴∠D=∠AFD,
∴AD=AF,即△ADF为等腰三角形;
(2)过A作AH⊥BC,
∵,DE⊥BC,
∴EF//AH,
∴EF是△BAH的中位线,
∵BE=2,
∴EH=2,
∵AB=AC,
∴BC=4BE=8,EC=HC+HE=BH+EH=6,
∵DA=AF=5,AC=AB=10,
∴DC=AD+AC=15,
∴.
18.解:(1)证明:四边形是平行四边形,
,.
,,
,
,
四边形为平行四边形.
(2),,
,
,
四边形为平行四边形.
上述结论成立,
由此可得出结论:若,,则四边形为平行四边形.
(3)在中,,
.
平分,
,
,
.
,
,
是的垂直平分线,
.
,
是等边三角形,
,
.
