五年级下册数学课件 - 1.3 长方体和正方体的体积 北京版(共24张PPT)
文档属性
| 名称 | 五年级下册数学课件 - 1.3 长方体和正方体的体积 北京版(共24张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 12:08:24 | ||
图片预览





文档简介
(共24张PPT)
五年级下册数学
长方体和正方体的体积
一、复习引入
它们都是由棱长为1厘米的小正方体拼成的。
你知道它们的体积分别是多少吗?
4立方厘米
5立方厘米
6立方厘米
猜想:
长方体的体积可能与哪些因素有关呢?
二、探索新知
二、探索新知
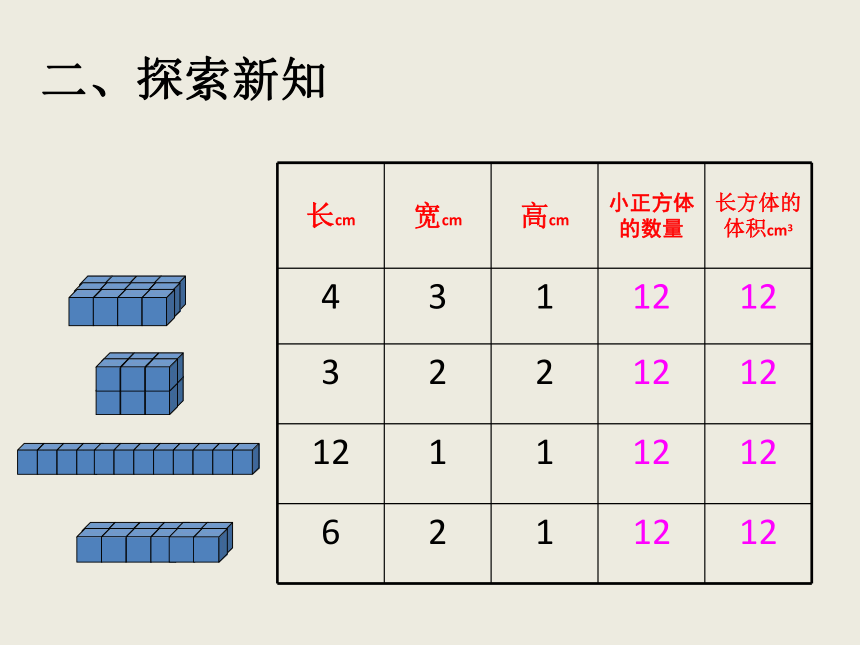
实验要求:四人小组,合作探究。用12个棱长为1厘米的小正方体摆成不同的长方体。说一说你是怎么摆的。把小组内摆法不同的长方体的相关数据填入下表。观察表格,说一说你的发现。
长\cm
宽\cm
高\cm
小正方体数量\个
体积\cm3
长方体A
长方体B
长方体C
长方体D
探究实验:
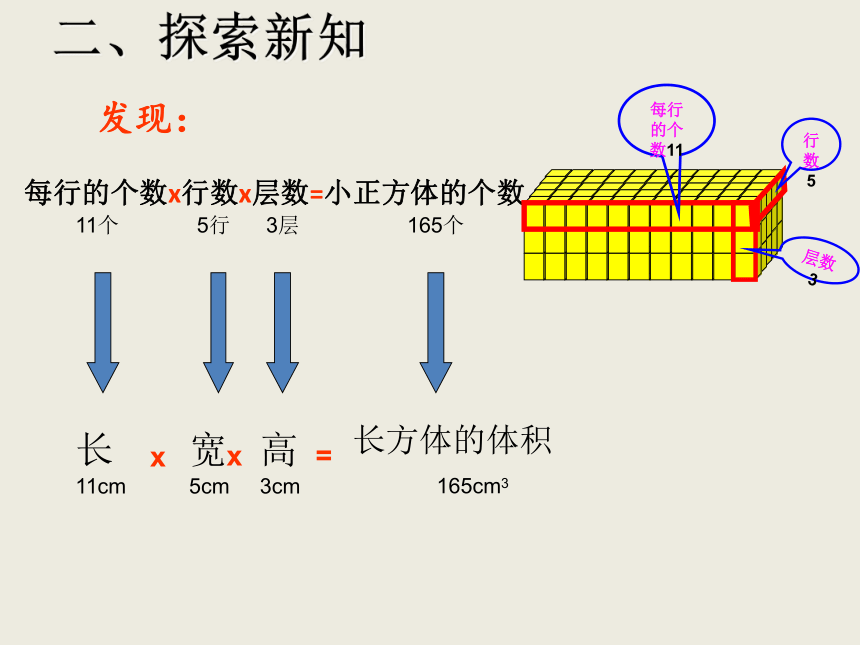
12
12
1
2
6
12
12
1
1
12
12
12
2
2
3
12
12
1
3
4
长方体的体积cm3
小正方体的数量
高cm
宽cm
长cm
二、探索新知
二、探索新知
探究实验:
你知道这个长方体是由多少个小正方体拼成的吗?
它的体积是多少呢?
165个
165cm3
每行的个数11
行数5
层数3
每行的个数x行数x层数=小正方体的个数
二、探索新知
长11cm
宽5cm
高3cm
长方体的体积
165cm3
11个
5行
3层
165个
发现:
x
x
=
每行的个数11
行数5
层数3
12
1
2
6
12
1
1
12
12
2
2
3
12
1
3
4
长方体的体积cm3
小正方体的数量
高cm
宽cm
长cm
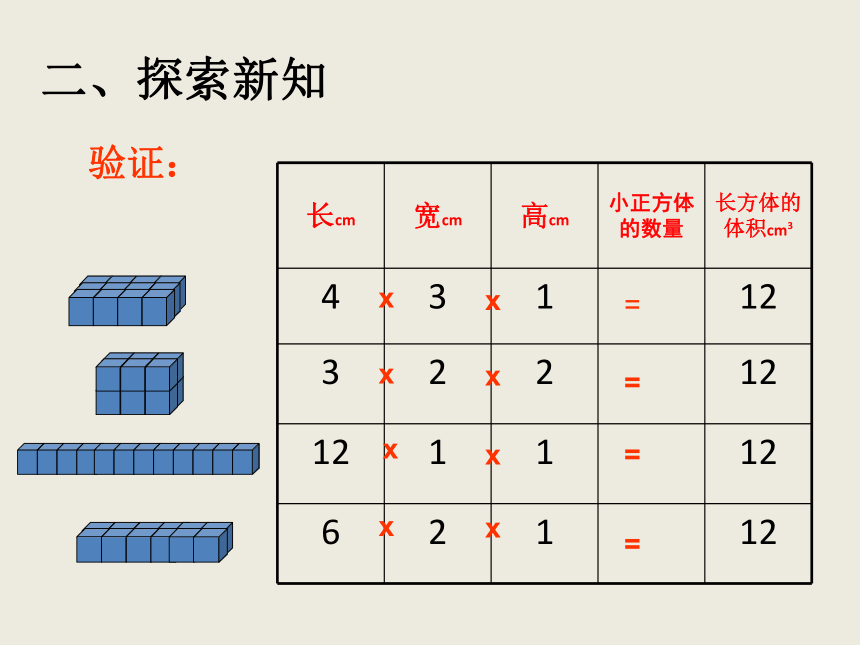
验证:
二、探索新知
x
x
x
x
x
x
x
x
=
=
=
=
如果用V表示长方体的体积,用a、b、h分别表示长方体的长、宽、高,长方体的体积公式可以写成:
V
=
abh
a
b
h
二、探索新知
结论:
长×宽×高
长方体的体积
=
长:
宽:
高:
V
=
abh
=13x9x5
=585(cm3)
二、探索新知
这个长方体的体积是多少呢?
13cm
9cm
5cm
正方体是长、宽、高相等的长方体,正方体的长、宽、高统称为棱长,所以:
正方体的体积=?
棱长×棱长×棱长
二、探索新知
正方体的体积=
提示:正方体是特殊的长方体哟!
如果用V表示正方体的体积,用a表示正方体的棱长,正方体的体积公式可以写成:
正方体的体积公式也可以写成:
V=a3
V=a
·
a
·
a
a·a·a也可以写作“a3”,读作“a的立方”,表示3个a相乘。
二、探索新知
二、探索新知
棱长:
V
=
a3
=6x6x6
=216(cm3)
这个正方体的体积是多少呢?
6cm
长方体或正方体底面的面积叫做底面积。
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
所以,长方体和正方体的体积也可以这样来计算:
长方体(或正方体)的体积=底面积×高
如果用S表示底面积,上面的公式可以写成:
V=Sh
底面积
底面积
同学们,再告诉你们一个秘密吧----
二、探索新知
回忆我们的探究过程:
猜想
----探究实验
----验证
----结论
从特殊到一般
迁移
----发现
三、知识应用
智力大闯关
第1关
判断:
1、将2个同样大小的正方体拼成一个长方体,它的表面积和体积都没有改变。(
)
×
×
2
一个正方体棱长3dm,它的体积是:
33
=9(dm3)
(
)
一块长方体肥皂的尺寸如下图,它的体积是多少?
V=a
b
h
=15×7×8
=840(cm3)
答:它的体积是840cm3。
第2关
三、知识应用
妈妈送给奶奶一个长方体形状的蛋糕,长2dm,宽2dm,高0.5dm。奶奶把它平均分成4块长方体的小蛋糕,每人分到多大的一块?
V=abh
=2×2×0.5
=2(dm3)
2÷4=0.5(dm3)
可以先求蛋糕的体积。
答:每人分得0.5dm3的一块蛋糕。
第3关
一根长方体木料,长5m,横截面的面积是0.06m2。这根木料的体积是多少?
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
0.06m2
第4关
这道题该用哪个公式来计算呢?
建筑工地要挖一个长50米、宽30米、深50厘米的长方体土坑,一共要挖出多少方的土?
在工程上,1m?的沙、石等均简称为1方。
第5关
建筑工地要挖一个长50米,宽30米,深50厘米的长方体土坑,一共要挖出多少方的土?
50厘米=0.5米
V=abh
=50×30×0.5
=750(方)
答:一共要挖出750方的土。
第5关
长方体的体积=
长×宽×高
V=a
b
h
正方体的体积=
棱长×棱长×棱长
V=a3
长方体(或正方体)的体积=底面积×高
V
=
sh
四、课堂总结
这节课学习了什么?
五年级下册数学
长方体和正方体的体积
一、复习引入
它们都是由棱长为1厘米的小正方体拼成的。
你知道它们的体积分别是多少吗?
4立方厘米
5立方厘米
6立方厘米
猜想:
长方体的体积可能与哪些因素有关呢?
二、探索新知
二、探索新知
实验要求:四人小组,合作探究。用12个棱长为1厘米的小正方体摆成不同的长方体。说一说你是怎么摆的。把小组内摆法不同的长方体的相关数据填入下表。观察表格,说一说你的发现。
长\cm
宽\cm
高\cm
小正方体数量\个
体积\cm3
长方体A
长方体B
长方体C
长方体D
探究实验:
12
12
1
2
6
12
12
1
1
12
12
12
2
2
3
12
12
1
3
4
长方体的体积cm3
小正方体的数量
高cm
宽cm
长cm
二、探索新知
二、探索新知
探究实验:
你知道这个长方体是由多少个小正方体拼成的吗?
它的体积是多少呢?
165个
165cm3
每行的个数11
行数5
层数3
每行的个数x行数x层数=小正方体的个数
二、探索新知
长11cm
宽5cm
高3cm
长方体的体积
165cm3
11个
5行
3层
165个
发现:
x
x
=
每行的个数11
行数5
层数3
12
1
2
6
12
1
1
12
12
2
2
3
12
1
3
4
长方体的体积cm3
小正方体的数量
高cm
宽cm
长cm
验证:
二、探索新知
x
x
x
x
x
x
x
x
=
=
=
=
如果用V表示长方体的体积,用a、b、h分别表示长方体的长、宽、高,长方体的体积公式可以写成:
V
=
abh
a
b
h
二、探索新知
结论:
长×宽×高
长方体的体积
=
长:
宽:
高:
V
=
abh
=13x9x5
=585(cm3)
二、探索新知
这个长方体的体积是多少呢?
13cm
9cm
5cm
正方体是长、宽、高相等的长方体,正方体的长、宽、高统称为棱长,所以:
正方体的体积=?
棱长×棱长×棱长
二、探索新知
正方体的体积=
提示:正方体是特殊的长方体哟!
如果用V表示正方体的体积,用a表示正方体的棱长,正方体的体积公式可以写成:
正方体的体积公式也可以写成:
V=a3
V=a
·
a
·
a
a·a·a也可以写作“a3”,读作“a的立方”,表示3个a相乘。
二、探索新知
二、探索新知
棱长:
V
=
a3
=6x6x6
=216(cm3)
这个正方体的体积是多少呢?
6cm
长方体或正方体底面的面积叫做底面积。
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
所以,长方体和正方体的体积也可以这样来计算:
长方体(或正方体)的体积=底面积×高
如果用S表示底面积,上面的公式可以写成:
V=Sh
底面积
底面积
同学们,再告诉你们一个秘密吧----
二、探索新知
回忆我们的探究过程:
猜想
----探究实验
----验证
----结论
从特殊到一般
迁移
----发现
三、知识应用
智力大闯关
第1关
判断:
1、将2个同样大小的正方体拼成一个长方体,它的表面积和体积都没有改变。(
)
×
×
2
一个正方体棱长3dm,它的体积是:
33
=9(dm3)
(
)
一块长方体肥皂的尺寸如下图,它的体积是多少?
V=a
b
h
=15×7×8
=840(cm3)
答:它的体积是840cm3。
第2关
三、知识应用
妈妈送给奶奶一个长方体形状的蛋糕,长2dm,宽2dm,高0.5dm。奶奶把它平均分成4块长方体的小蛋糕,每人分到多大的一块?
V=abh
=2×2×0.5
=2(dm3)
2÷4=0.5(dm3)
可以先求蛋糕的体积。
答:每人分得0.5dm3的一块蛋糕。
第3关
一根长方体木料,长5m,横截面的面积是0.06m2。这根木料的体积是多少?
0.06×5=0.3(m3)
答:这根木料的体积是0.3m3。
0.06m2
第4关
这道题该用哪个公式来计算呢?
建筑工地要挖一个长50米、宽30米、深50厘米的长方体土坑,一共要挖出多少方的土?
在工程上,1m?的沙、石等均简称为1方。
第5关
建筑工地要挖一个长50米,宽30米,深50厘米的长方体土坑,一共要挖出多少方的土?
50厘米=0.5米
V=abh
=50×30×0.5
=750(方)
答:一共要挖出750方的土。
第5关
长方体的体积=
长×宽×高
V=a
b
h
正方体的体积=
棱长×棱长×棱长
V=a3
长方体(或正方体)的体积=底面积×高
V
=
sh
四、课堂总结
这节课学习了什么?
