2020-2021学年八年级数学苏科版下册9.3 平行四边形的定义及其性质提优训练(Word版 含答案)
文档属性
| 名称 | 2020-2021学年八年级数学苏科版下册9.3 平行四边形的定义及其性质提优训练(Word版 含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 171.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-12 23:58:44 | ||
图片预览

文档简介
9.3 平行四边形(1)提优训练
一、选择题
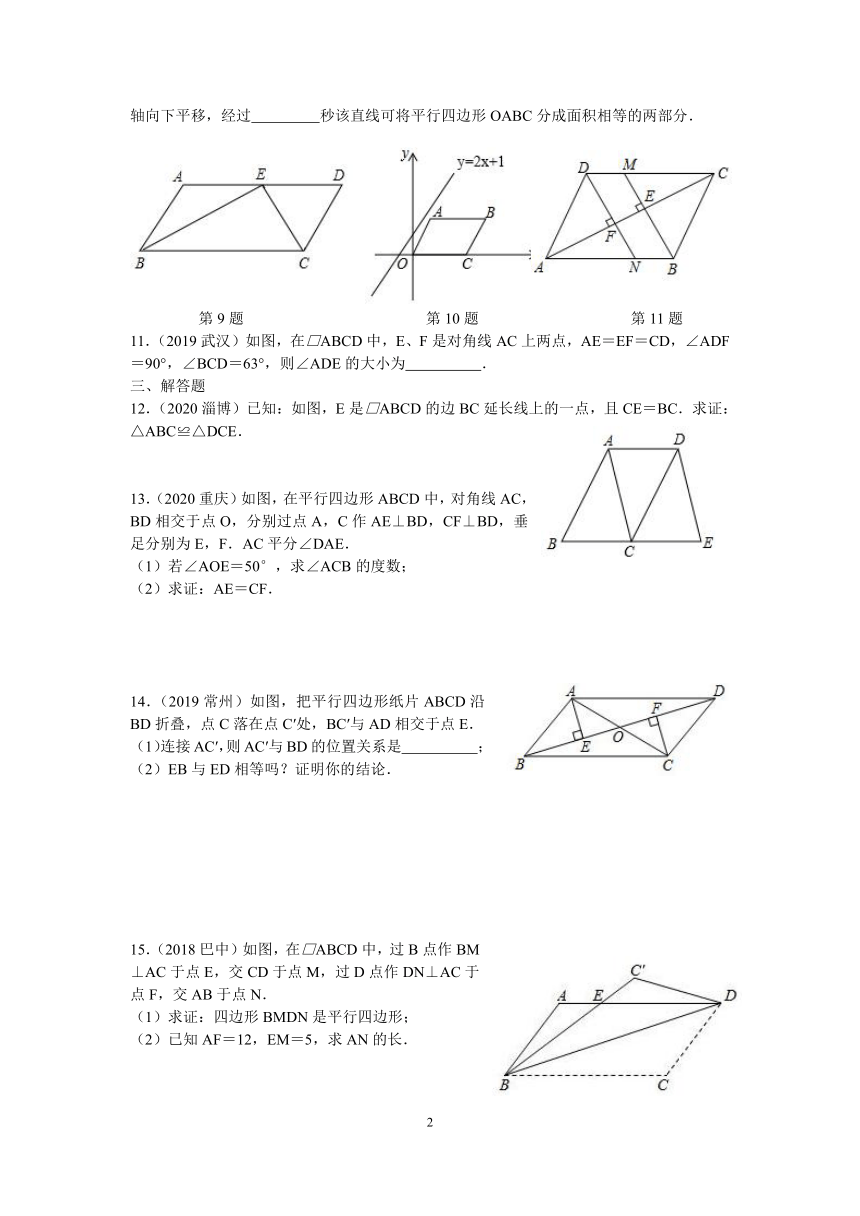
1.(2020温州)如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作□BCDE,则∠E的度数为( )
A.40° B.50° C.60° D.70°
第1题 第2题 第3题
2.(2020益阳)如图,□ABCD的对角线AC,BD交于点O,若AC=6,BD=8,则AB的长可能是( )
A.10 B.8 C.7 D.6
3.(2020邵阳)如图,四边形ABCD是平行四边形,点E,B,D,F在同一条直线上,请添加一个条件使得△ABE≌△CDF,下列不正确的是( )
A.AE=CF B.∠AEB=∠CFD C.∠EAB=∠FCD D.BE=DF
4.(2019遂宁)如图,□ABCD中,对角线AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,若□ABCD的周长为28,则△ABE的周长为( )
A.28 B.24 C.21 D.14
第4题 第5题 第6题
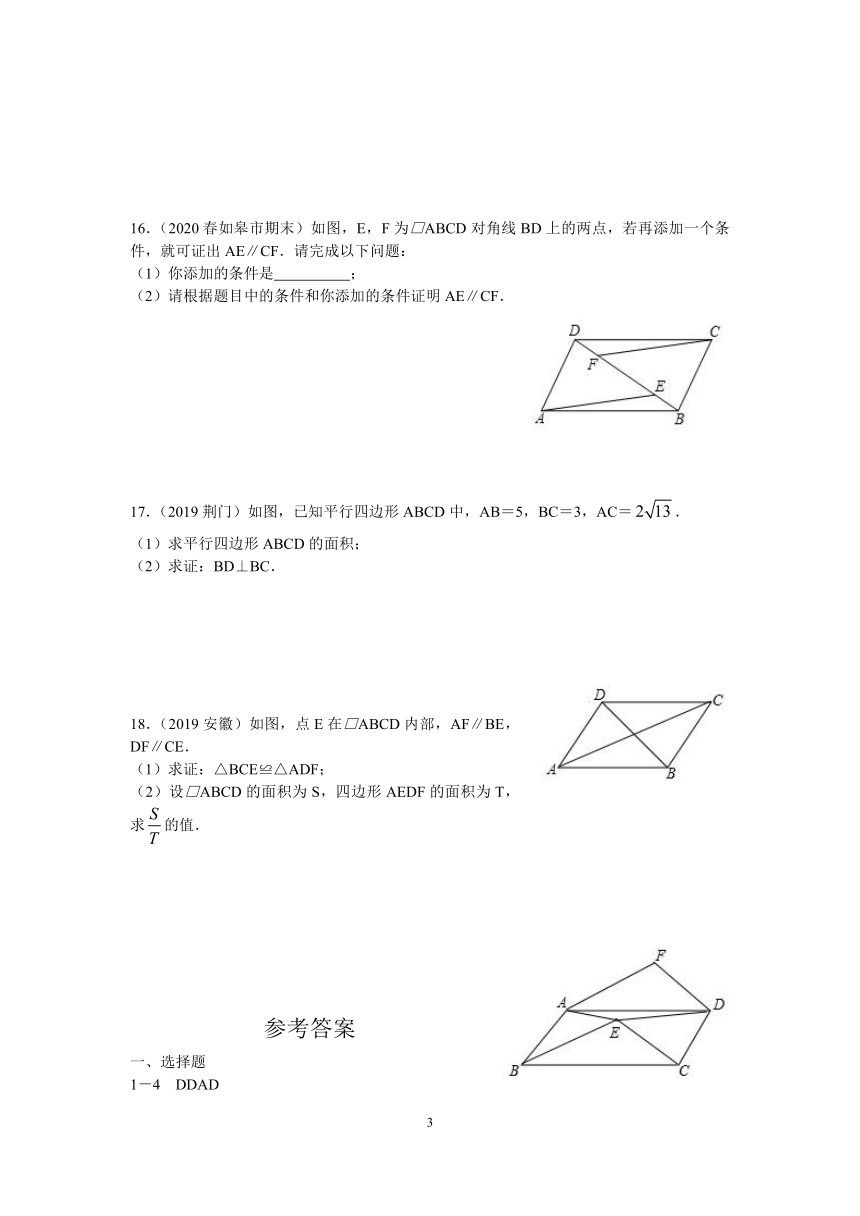
二、填空题
5.(2020金华)如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是 °.
6.(2018十堰)如图,已知□ABCD的对角线AC,BD相交于点O,且AC=8,BD=10,AB=5,则△OCD的周长为 .
7.(2017通辽)在□ABCD中,AE平分∠BAD交边BC于E,DF平分∠ADC交边BC于F,若AD=11,EF=5,则AB= .
8.(2019福建)在平面直角坐标系xOy中,□OABC的三个顶点O(0,0)、A(3,0)、B(4,2),则其第四个顶点是 .
9.(2020包头)如图,在□ABCD中,AB=2,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为 .
10.(2019春常州期中)如图,在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点B(6,2),C(4,0),直线y=2x+1以每秒1个单位长度的速度沿y轴向下平移,经过 秒该直线可将平行四边形OABC分成面积相等的两部分.
第9题 第10题 第11题
11.(2019武汉)如图,在□ABCD中,E、F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为 .
三、解答题
12.(2020淄博)已知:如图,E是□ABCD的边BC延长线上的一点,且CE=BC.求证:△ABC≌△DCE.
13.(2020重庆)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD,CF⊥BD,垂足分别为E,F.AC平分∠DAE.
(1)若∠AOE=50°,求∠ACB的度数;
(2)求证:AE=CF.
14.(2019常州)如图,把平行四边形纸片ABCD沿BD折叠,点C落在点C′处,BC′与AD相交于点E.
(1)连接AC′,则AC′与BD的位置关系是 ;
(2)EB与ED相等吗?证明你的结论.
15.(2018巴中)如图,在□ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.
16.(2020春如皋市期末)如图,E,F为□ABCD对角线BD上的两点,若再添加一个条件,就可证出AE∥CF.请完成以下问题:
(1)你添加的条件是 ;
(2)请根据题目中的条件和你添加的条件证明AE∥CF.
17.(2019荆门)如图,已知平行四边形ABCD中,AB=5,BC=3,AC=.
(1)求平行四边形ABCD的面积;
(2)求证:BD⊥BC.
18.(2019安徽)如图,点E在□ABCD内部,AF∥BE,DF∥CE.
(1)求证:△BCE≌△ADF;
(2)设□ABCD的面积为S,四边形AEDF的面积为T,求的值.
参考答案
一、选择题
1-4 DDAD
二、填空题
5.30 6.14 7.8或3 8.(1,2) 9.16 10.6 11.21°
三、解答题
12.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠DCE,
在△ABC和△DCE中,
∵,
∴△ABC≌△DCE(SAS).
13.(1)解:∵AE⊥BD,
∴∠AEO=90°,
∵∠AOE=50°,
∴∠EAO=40°,
∵CA平分∠DAE,
∴∠DAC=∠EAO=40°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ACB=∠DAC=40°;
(2)证明:∵四边形ABCD是平行四边形,
∴OA=OC,
∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO=90°,
∵∠AOE=∠COF,
∴△AEO≌△CFO(AAS),
∴AE=CF.
14.解:(1)连接AC′,∵四边形ABCD平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
由折叠知,BC'=BC,∠C'BD=∠CBD,
∴AD=BC',∠ADB=∠C'BD,
∴BE=DE,
∴AE=C'E,
∴∠DAC'=(180°-∠AEC')=90°-∠AEC',
同理:∠ADB=90°-∠BED,
∵∠AEC'=∠BED,
∴∠DAC'=∠ADB,
∴AC'∥BD,
故答案为:AC′∥BD;
(2)EB与ED相等.
由折叠可得,∠CBD=∠C'BD,
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠EDB=∠CBD,
∴BE=DE.
15.(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,
∵BM⊥AC,DN⊥AC,
∴DN∥BM,
∴四边形BMDN是平行四边形;
(2)解:∵四边形BMDN是平行四边形,
∴DM=BN,
∵CD=AB,CD∥AB,
∴CM=AN,∠MCE=∠NAF,
∵∠CEM=∠AFN=90°,
∴△CEM≌△AFN,
∴FN=EM=5,
在Rt△AFN中,.
16.解:(1)添加的条件是:DF=BE,
故答案为:DF=BE;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADE=∠CBF,
∵DF=BE,
∴BD-DF=BD-BE,
∴BF=DE,
在△ADE和△CBF中,
∵,
∴△ADE≌△CBF(SAS)
∴∠AED=∠CFB,
∴AE∥CF.
17.解:(1)作CE⊥AB交AB的延长线于点E,如图:
设BE=x,CE=h
在Rt△CEB中:x2+h2=9①
在Rt△CEA中:(5+x)2+h2=②
联立①②解得:x=,h=
∴平行四边形ABCD的面积=AB?h=12;
(2)作DF⊥AB,垂足为F
∴∠DFA=∠CEB=90°
∵平行四边形ABCD
∴AD=BC,AD∥BC
∴∠DAF=∠CBE
又∵∠DFA=∠CEB=90°,AD=BC
∴△ADF≌△BCE(AAS)
∴AF=BE=,BF=5-=,DF=CE=
在Rt△DFB中:BD2=DF2+BF2==16
∴BD=4
∵BC=3,DC=5
∴CD2=DB2+BC2
∴BD⊥BC.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ABC+∠BAD=180°,
∵AF∥BE,
∴∠EBA+∠BAF=180°,
∴∠CBE=∠DAF,
同理得∠BCE=∠ADF,
在△BCE和△ADF中,
∵ ,
∴△BCE≌△ADF(ASA);
(2)解:∵点E在□ABCD内部,
∴S△BEC+S△AED=S□ABCD,
由(1)知:△BCE≌△ADF,
∴S△BCE=S△ADF,
∴S四边形AEDF=S△ADF+S△AED=S△BEC+S△AED=S□ABCD,
∵□ABCD的面积为S,四边形AEDF的面积为T,
∴.
1
一、选择题
1.(2020温州)如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作□BCDE,则∠E的度数为( )
A.40° B.50° C.60° D.70°
第1题 第2题 第3题
2.(2020益阳)如图,□ABCD的对角线AC,BD交于点O,若AC=6,BD=8,则AB的长可能是( )
A.10 B.8 C.7 D.6
3.(2020邵阳)如图,四边形ABCD是平行四边形,点E,B,D,F在同一条直线上,请添加一个条件使得△ABE≌△CDF,下列不正确的是( )
A.AE=CF B.∠AEB=∠CFD C.∠EAB=∠FCD D.BE=DF
4.(2019遂宁)如图,□ABCD中,对角线AC、BD相交于点O,OE⊥BD交AD于点E,连接BE,若□ABCD的周长为28,则△ABE的周长为( )
A.28 B.24 C.21 D.14
第4题 第5题 第6题
二、填空题
5.(2020金华)如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是 °.
6.(2018十堰)如图,已知□ABCD的对角线AC,BD相交于点O,且AC=8,BD=10,AB=5,则△OCD的周长为 .
7.(2017通辽)在□ABCD中,AE平分∠BAD交边BC于E,DF平分∠ADC交边BC于F,若AD=11,EF=5,则AB= .
8.(2019福建)在平面直角坐标系xOy中,□OABC的三个顶点O(0,0)、A(3,0)、B(4,2),则其第四个顶点是 .
9.(2020包头)如图,在□ABCD中,AB=2,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为 .
10.(2019春常州期中)如图,在平面直角坐标系中,平行四边形OABC的边OC落在x轴的正半轴上,且点B(6,2),C(4,0),直线y=2x+1以每秒1个单位长度的速度沿y轴向下平移,经过 秒该直线可将平行四边形OABC分成面积相等的两部分.
第9题 第10题 第11题
11.(2019武汉)如图,在□ABCD中,E、F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为 .
三、解答题
12.(2020淄博)已知:如图,E是□ABCD的边BC延长线上的一点,且CE=BC.求证:△ABC≌△DCE.
13.(2020重庆)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD,CF⊥BD,垂足分别为E,F.AC平分∠DAE.
(1)若∠AOE=50°,求∠ACB的度数;
(2)求证:AE=CF.
14.(2019常州)如图,把平行四边形纸片ABCD沿BD折叠,点C落在点C′处,BC′与AD相交于点E.
(1)连接AC′,则AC′与BD的位置关系是 ;
(2)EB与ED相等吗?证明你的结论.
15.(2018巴中)如图,在□ABCD中,过B点作BM⊥AC于点E,交CD于点M,过D点作DN⊥AC于点F,交AB于点N.
(1)求证:四边形BMDN是平行四边形;
(2)已知AF=12,EM=5,求AN的长.
16.(2020春如皋市期末)如图,E,F为□ABCD对角线BD上的两点,若再添加一个条件,就可证出AE∥CF.请完成以下问题:
(1)你添加的条件是 ;
(2)请根据题目中的条件和你添加的条件证明AE∥CF.
17.(2019荆门)如图,已知平行四边形ABCD中,AB=5,BC=3,AC=.
(1)求平行四边形ABCD的面积;
(2)求证:BD⊥BC.
18.(2019安徽)如图,点E在□ABCD内部,AF∥BE,DF∥CE.
(1)求证:△BCE≌△ADF;
(2)设□ABCD的面积为S,四边形AEDF的面积为T,求的值.
参考答案
一、选择题
1-4 DDAD
二、填空题
5.30 6.14 7.8或3 8.(1,2) 9.16 10.6 11.21°
三、解答题
12.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠B=∠DCE,
在△ABC和△DCE中,
∵,
∴△ABC≌△DCE(SAS).
13.(1)解:∵AE⊥BD,
∴∠AEO=90°,
∵∠AOE=50°,
∴∠EAO=40°,
∵CA平分∠DAE,
∴∠DAC=∠EAO=40°,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ACB=∠DAC=40°;
(2)证明:∵四边形ABCD是平行四边形,
∴OA=OC,
∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO=90°,
∵∠AOE=∠COF,
∴△AEO≌△CFO(AAS),
∴AE=CF.
14.解:(1)连接AC′,∵四边形ABCD平行四边形,
∴AD=BC,AD∥BC,
∴∠ADB=∠CBD,
由折叠知,BC'=BC,∠C'BD=∠CBD,
∴AD=BC',∠ADB=∠C'BD,
∴BE=DE,
∴AE=C'E,
∴∠DAC'=(180°-∠AEC')=90°-∠AEC',
同理:∠ADB=90°-∠BED,
∵∠AEC'=∠BED,
∴∠DAC'=∠ADB,
∴AC'∥BD,
故答案为:AC′∥BD;
(2)EB与ED相等.
由折叠可得,∠CBD=∠C'BD,
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠EDB=∠CBD,
∴BE=DE.
15.(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,
∵BM⊥AC,DN⊥AC,
∴DN∥BM,
∴四边形BMDN是平行四边形;
(2)解:∵四边形BMDN是平行四边形,
∴DM=BN,
∵CD=AB,CD∥AB,
∴CM=AN,∠MCE=∠NAF,
∵∠CEM=∠AFN=90°,
∴△CEM≌△AFN,
∴FN=EM=5,
在Rt△AFN中,.
16.解:(1)添加的条件是:DF=BE,
故答案为:DF=BE;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADE=∠CBF,
∵DF=BE,
∴BD-DF=BD-BE,
∴BF=DE,
在△ADE和△CBF中,
∵,
∴△ADE≌△CBF(SAS)
∴∠AED=∠CFB,
∴AE∥CF.
17.解:(1)作CE⊥AB交AB的延长线于点E,如图:
设BE=x,CE=h
在Rt△CEB中:x2+h2=9①
在Rt△CEA中:(5+x)2+h2=②
联立①②解得:x=,h=
∴平行四边形ABCD的面积=AB?h=12;
(2)作DF⊥AB,垂足为F
∴∠DFA=∠CEB=90°
∵平行四边形ABCD
∴AD=BC,AD∥BC
∴∠DAF=∠CBE
又∵∠DFA=∠CEB=90°,AD=BC
∴△ADF≌△BCE(AAS)
∴AF=BE=,BF=5-=,DF=CE=
在Rt△DFB中:BD2=DF2+BF2==16
∴BD=4
∵BC=3,DC=5
∴CD2=DB2+BC2
∴BD⊥BC.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠ABC+∠BAD=180°,
∵AF∥BE,
∴∠EBA+∠BAF=180°,
∴∠CBE=∠DAF,
同理得∠BCE=∠ADF,
在△BCE和△ADF中,
∵ ,
∴△BCE≌△ADF(ASA);
(2)解:∵点E在□ABCD内部,
∴S△BEC+S△AED=S□ABCD,
由(1)知:△BCE≌△ADF,
∴S△BCE=S△ADF,
∴S四边形AEDF=S△ADF+S△AED=S△BEC+S△AED=S□ABCD,
∵□ABCD的面积为S,四边形AEDF的面积为T,
∴.
1
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
