2020-2021学年七年级数学北师大版下册《2.3平行线的性质》培优训练(Word版 附答案)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版下册《2.3平行线的性质》培优训练(Word版 附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 238.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 00:00:00 | ||
图片预览



文档简介
2020-2021年度北师大版七年级数学下册《2.3平行线的性质》培优训练(附答案)
1.如图,直线MN∥PQ,点A是MN上一点,∠MAC的角平分线交PQ于点B,若∠1=20°,∠2=116°,则∠3的大小为( )
A.136° B.138° C.146° D.148°
2.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为( )
A.114° B.142° C.147° D.156°
3.如图,AB∥DE,那么∠BCD=( )
A.180°+∠1﹣∠2 B.∠1+∠2
C.∠2﹣∠1 D.180°+∠2﹣2∠1
4.如图,AB∥CD,则下列等式正确的是( )
A.∠1=∠2+∠3 B.∠1﹣∠2=180°﹣∠3
C.∠1﹣∠3=180°﹣∠2 D.∠1+∠2+∠3=180°
5.如图,已知AB∥DE,∠ABC=130°,∠CDE=110°,则∠BCD的度数为( )
A.50° B.60° C.70° D.80°
6.如图,已知AB∥DF,DE和AC分别平分∠CDF和∠BAE,若∠DEA=46°,∠ACD=56°,则∠CDF的度数为( )
A.42° B.43° C.44° D.45°
7.如图,直线AB∥CD,点F在直线AB上,点N在直线CD上,∠EFA=25°,∠FGH=90°,∠HMN=25°,∠CNP=30°,则∠GHM=( )
A.45° B.50° C.55° D.60°
8.如图,∠BCD=90°,AB∥DE,若∠a=40°,则∠β的大小为( )
A.40° B.50 C.130° D.140°
9.已知直线m∥n,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),并且顶点A,C分别落在直线m,n上,若∠1=38°,则∠2的度数是( )
A.20° B.22° C.28° D.38°
10.两个角的两边两两互相平行,且一个角的等于另一个角的,则这两个角中较小角的度数为 °.
11.如图,直线AB、CD被直线EF所截,AB∥CD,DG⊥BF于点G,若∠1=130°,则∠2的度数为 .
12.如图,如果AB∥CD,则角α=130°,γ=20°,则β= .
13.如图,已知AB∥DE,∠ABC=76°,∠CDE=150°,则∠BCD的度数为 °.
14.如图,已知AB∥DE,∠ABC=135°,∠CDE=70°,则∠BCD= .
15.如图,已知直线l1∥l2,∠1=30°,则∠2+∠3= .
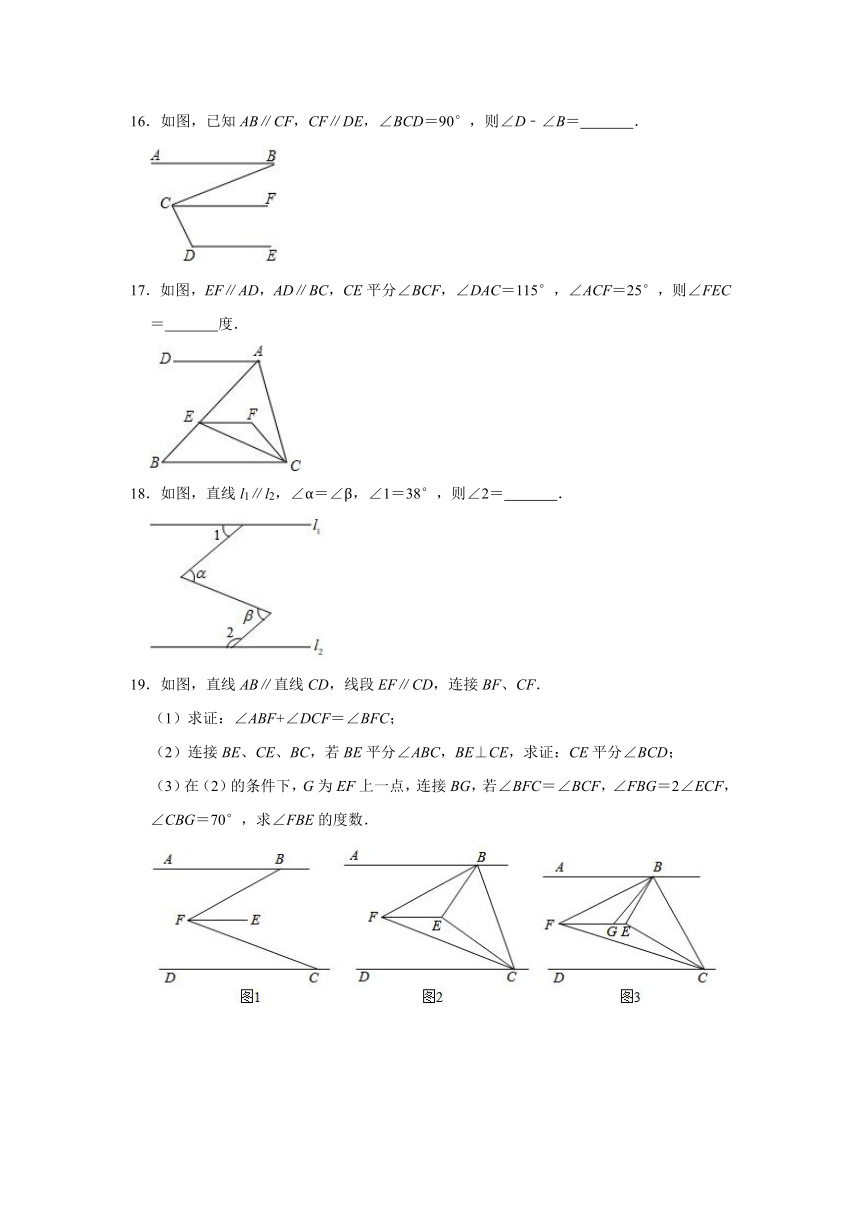
16.如图,已知AB∥CF,CF∥DE,∠BCD=90°,则∠D﹣∠B= .
17.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=115°,∠ACF=25°,则∠FEC= 度.
18.如图,直线l1∥l2,∠α=∠β,∠1=38°,则∠2= .
19.如图,直线AB∥直线CD,线段EF∥CD,连接BF、CF.
(1)求证:∠ABF+∠DCF=∠BFC;
(2)连接BE、CE、BC,若BE平分∠ABC,BE⊥CE,求证:CE平分∠BCD;
(3)在(2)的条件下,G为EF上一点,连接BG,若∠BFC=∠BCF,∠FBG=2∠ECF,∠CBG=70°,求∠FBE的度数.
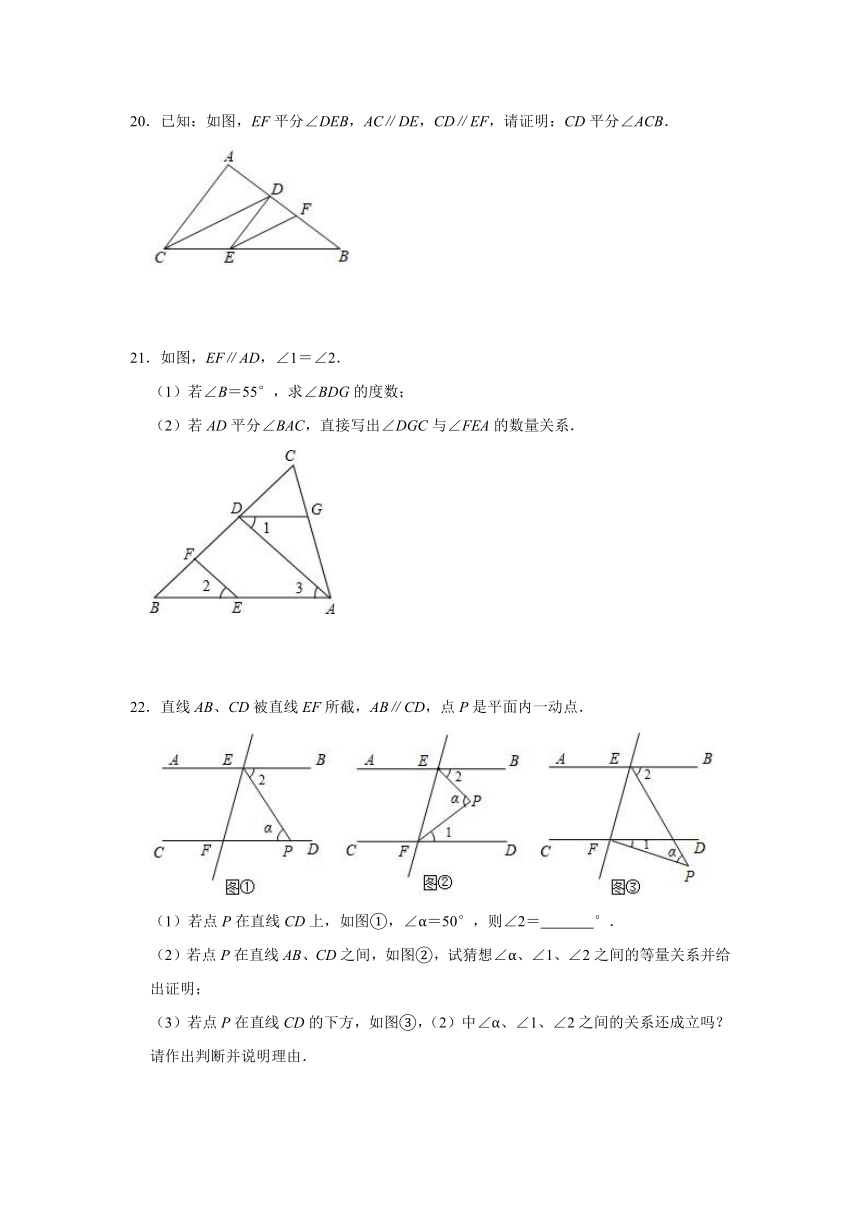
20.已知:如图,EF平分∠DEB,AC∥DE,CD∥EF,请证明:CD平分∠ACB.
21.如图,EF∥AD,∠1=∠2.
(1)若∠B=55°,求∠BDG的度数;
(2)若AD平分∠BAC,直接写出∠DGC与∠FEA的数量关系.
22.直线AB、CD被直线EF所截,AB∥CD,点P是平面内一动点.
(1)若点P在直线CD上,如图①,∠α=50°,则∠2= °.
(2)若点P在直线AB、CD之间,如图②,试猜想∠α、∠1、∠2之间的等量关系并给出证明;
(3)若点P在直线CD的下方,如图③,(2)中∠α、∠1、∠2之间的关系还成立吗?请作出判断并说明理由.
23.已知直线AB∥CD,直线EF分别交AB、CD于点A、C,CM是∠ACD的平分线,CM交AB于点H,过点A作AG⊥AC交CM于点G.
(1)如图1,点G在CH的延长线上时,若∠GAB=36°,求∠MCD的度数;
(2)如图2,点G在CH上时,试说明2∠MCD+∠GAB=90°.
24.(1)如图①,AB∥CD,∠A=43°,∠C=33°,求∠APC的度数;
(2)如图②,AB∥CD,当点P在线段BD上移动时,设∠BAP=α,∠DCP=β,写出∠APC与α,β之间的数量关系,并说明理由;
(3)在(2)的条件下,如果点P在射线DM上运动,请你直接写出∠APC与α,β之间的数量关系.
参考答案
1.解:延长QC交AB于D,
∵MN∥PQ,
∴∠2+∠MAB=180°,
∵∠2=116°,
∴∠MAB=180°﹣116°=64°,
∵AB平分∠MAC,
∴∠MAB=∠BAC=64°,
△BDQ中,∠BDQ=∠2﹣∠1=116°﹣20°=96°,
∴∠ADC=180°﹣96°=84°,
△ADC中,∠3=∠BAC+∠ADC=64°+84°=148°.
故选:D.
2.解:∵∠1=24°,CE⊥直线c于点E,
∴∠EAC=90°﹣∠1=90°﹣24°=66°,
∵a∥b,
∴∠EAC=∠ABD=66°,
∵∠ABD的平分线交直线a于点C,
∴∠CBD=,
∴∠2=180°﹣∠CBD=180°﹣33°=147°,
故选:C.
3.解:过点C作CF∥AB,如图:
∵AB∥DE,
∴AB∥DE∥CF,
∴∠BCF=∠1①,∠2+∠DCF=180°②,
∴①+②得,∠BCF+∠DCF+∠2=∠1+180°,即∠BCD=180°+∠1﹣∠2.
故选:A.
4.解:如右图所示,
∵CD∥AB,
∴∠4=∠3,
∵∠4=∠2+(180°﹣∠1),
∴∠3=∠2+(180°﹣∠1),
∴∠1﹣∠2=180°﹣∠3,
故选:B.
5.解:作DE的反向延长线交BC于M,
∵AB∥DE,∠ABC=130°,
∴∠BMD=∠ABC=130°,
∴∠CMD=180°﹣∠BMD=50°,
∵∠CDE=110°,
∴∠BCD=∠CDE﹣∠CMD=110°﹣50°=60°,
故选:B.
6.解:过点C作CN∥AB,过点E作EM∥AB,
∵FD∥AB,CN∥AB,EM∥AB,
∴AB∥CN∥EM∥FD
∴∠BAC=∠NCA,∠NCD=∠FDC,∠FDE=∠DEM,∠MEA=∠EAB.
∴∠DEA=∠FDE+∠EAB,
∠ACD=∠BAC+∠FDC.
又∵DE和AC分别平分∠CDF和∠BAE,
∴∠FDC=2∠FDE=2∠EDC,∠BAE=2∠BAC=2∠EAC
∴56°=∠BAC+2∠FDE①,
46°=∠FDE+2∠BAC②.
①+②,得3(∠BAC+∠FDE)=102°,
∴∠BAC+∠FDE=34°③.
①﹣③,得∠FDE=22°.
∴∠CDF=2∠FDE=44°.
故选:C.
7.解:延长HG交直线AB于点K,延长PM交直线AB于点S.
∵AB∥CD,
∴∠KSM=∠CNP=30°.
∵∠EFA=∠KFG=25°,∠KGF=180°﹣∠FGH=90°,
∠SMH=180°﹣∠HMN=155°,
∴∠SKH=∠KFG+∠KGF=25°+90°=115°.
∵∠SKH+∠GHM+∠SMH+∠KSM=360°,
∴∠GHM=360°﹣115°﹣155°﹣30°=60°.
故选:D.
8.解:过C作CF∥AB,
∵AB∥DE,
∴AB∥CF∥DE,
∴∠1=∠α=40°,∠2=180°﹣∠β,
∵∠BCD=90°,
∴∠1+∠2=40°+180°﹣∠β=90°,
∴∠β=130°.
故选:C.
9.解:∵∠ABC=30°,∠BAC=90°,
∴∠ACB=60°,
过C作CD∥直线m,
∵直线m∥n,
∴CD∥直线m∥直线n,
∴∠1=∠ACD,∠2=∠BCD,
∵∠1=38°,
∴∠ACD=38°,
∴∠2=∠BCD=60°﹣38°=22°,
故选:B.
10.解:∵一个角的等于另一个角的,
∴这两个角不相等,
设其中一个角的度数为x°,另一个角的度数为x=x°,
∵两个角的两边两两互相平行,
∴x+x=180,
解得:x=72,
即较小角的度数是72°,
故选:72.
11.解:∵AB∥CD,∠1=130°,
∴∠CFB=∠1=130°,
∴∠BFD=180°﹣∠CFB=180°﹣130°=50°,
∵DG⊥BF,
∴∠DGF=90°,
∴∠2=90°﹣∠BFD=90°﹣50°=40°,
故答案为40°.
12.解:如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠AEF=180°,∠D=∠FED,
∴∠AEF=180°﹣130°=50°,∠FED=20°,
∴∠AED=∠AEF+∠FED=50°+20°=70°.
即β=70°.
故答案为:70°.
13.解:过点C作CF∥AB,
∵AB∥DE,
∴AB∥DE∥CF,
∴∠ABC=∠BCF,∠CDE+∠DCF=180°,
∵∠ABC=76°,∠CDE=150°,
∴∠BCF=76°,∠DCF=30°,
∴∠BCD=46°,
故答案为:46.
14.解:如图,延长CB交ED的延长线于G.
∵AB∥DF,
∴∠1=∠ABC=135°,
∵∠1=∠CDG+∠C,∠CDG=180°﹣∠CDE=110°,
∴∠BCD=135°﹣110°=25°,
故答案为25°.
15.解:如图.
∵直线l1∥l2,
∴∠3+∠4=180°,
∵∠2=∠1+∠4,
∴∠3+∠4+∠2=180°+∠1+∠4,
∵∠1=30°,
∴∠2+∠3=180°+30°=210°.
故答案为210°
16.解:∵AB∥CF,
∵∠B=∠1,
∵CF∥DE,
∴∠D+∠2=180°,即∠2=180°﹣∠D,
∵∠BCD=90°,
∴∠1+∠2=90°,即∠B+180°﹣∠D=90°,
∴∠D﹣∠B=90°.
故答案为:90°.
17.解:∵AD∥BC,
∴∠ACB=180°﹣∠DAC=180°﹣115°=65°,
∵∠ACF=25°,
∴∠BCF=∠ACB﹣∠ACF=65°﹣25°=40°,
∵CE平分∠BCF,
∴∠BCE=∠BCF=×40°=20°,
∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠FEC=∠BCE=20°.故答案为:20.
18.解:延长AB交l2于点E,
∵∠α=∠β,
∴AB∥DC,
∴∠3+∠2=180°,
∵l1∥l2,
∴∠1=∠3=38°,
∴∠2=180°﹣38°=142°,故答案为:142°.
19.证明:(1)∵AB∥CD,EF∥CD,
∴AB∥EF,
∴∠ABF=∠BFE,
∵EF∥CD,
∴∠DCF=∠EFC,
∴∠BFC=∠BFE+∠EFC=∠ABF+∠DCF;
(2)∵BE⊥EC,
∴∠BEC=90°,
∴∠EBC+∠BCE=90°,
由(1)可得:∠BFC=∠ABE+∠ECD=90°,
∴∠ABE+∠ECD=∠EBC+∠BCE,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ECD=∠BCE,
∴CE平分∠BCD;
(3)设∠BCE=β,∠ECF=γ,
∵CE平分∠BCD,
∴∠DCE=∠BCE=β,
∴∠DCF=∠DCE﹣∠ECF=β﹣γ,
∴∠EFC=β﹣γ,
∵∠BFC=∠BCF,
∴∠BFC=∠BCE+∠ECF=γ+β,
∴∠ABF=∠BFE=2γ,
∵∠FBG=2∠ECF,
∴∠FBG=2γ,
∴∠ABE+∠DCE=∠BEC=90°,
∴∠ABE=90°﹣β,
∴∠GBE=∠ABE﹣∠ABF﹣∠FBG=90°﹣β﹣2γ﹣2γ,
∵BE平分∠ABC,
∴∠CBE=∠ABE=90°﹣β,
∴∠CBG=∠CBE+∠GBE,
∴70°=90°﹣β+90°﹣β﹣2γ﹣2γ,
整理得:2γ+β=55°,
∴∠FBE=∠FBG+∠GBE=2γ+90°﹣β﹣2γ﹣2γ=90°﹣(2γ+β)=35°.
20.解:∵AC∥DE,
∴∠ACD=∠CDE,
∵CD∥EF,
∴∠DCB=∠FEB,∠CDE=∠DEF,
∴∠ACD=∠DEF,
又∵EF平分∠DEB,
∴∠DEF=∠FEB,
∴∠ACD=∠DCB,
∴CD平分∠ACB.
21.解:(1)∵EF∥AD,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴DG∥BA,
∴∠B+∠BDG=180°,
∵∠B=55°,
∴∠BDG=125°;
(2)∠DGC+∠FEA=180°,
理由:∵AD平分∠BAC,
∴∠BAC=2∠3,
由(1)知,DG∥BA,
∴∠CGD=∠BAC,
∴∠CGD=2∠3,
∵EF∥AD,
∴∠FEA+∠3=180°,
∴∠DGC+∠FEA=180°.
22.解:①∵AB∥CD,∠α=50°
∴∠2=∠α=50°,
故答案为50;
(2)∠α=∠1+∠2.
证明:过P作PG∥AB,
∵AB∥CD,
∴PG∥AB∥CD,
∴∠2=∠EPG,∠1=∠FPG,
∵∠α=∠EPF=∠EPG+∠FPG,
∴∠α=∠1+∠2;
(3)不成立.
理由:过P作PH∥AB,
∵AB∥CD,
∴PH∥AB∥CD,
∴∠2=∠EPH,∠1=∠FPH,
∵∠α=∠EPF=∠EPH﹣∠FPH,
∴∠α=∠2﹣∠1,
故不成立.
23.解:(1)∵AG⊥AC,∠GAB=36°,
∴∠CAH=90°﹣36°=54°,
∵AB∥CD,
∴∠ACD+∠CAH=180°,
∴∠ACD=126°,
∵CM是∠ACD的平分线,
∴∠ACH=∠DCM=63°.
(2)∵∠ACH=∠DCM,
∴∠ACD=2∠MCD,
由(1)得ACD+∠CAH=180°,
∵AG⊥AC,
∴∠CAG=90°,
∴2∠MCD+90°+∠GAB=180°,
∴2∠MCD+∠GAB=90°.
24.解:(1)过P点作PE∥AB,
∴∠APE=∠A,
∵AB∥CD,
∴PE∥CD,
∴∠EPC=∠C,
∵∠APC=∠APE+∠EPC,
∴∠APC=∠A+∠C
∵∠A=43°,∠C=33°,
∴∠APC=43°+33°=76°;
(2)∠APC=α+β.
理由:过P点作PF∥AB,
∴∠APF=∠BAP,
∵AB∥CD,
∴PF∥CD,
∴∠FPC=∠PCD,
∵∠APC=∠APF+∠FPC,
∴∠APC=∠BAP+∠PCD;
∵∠BAP=α,∠DCP=β,
∴∠APC=α+β;
(3)∠APC=α﹣β.
理由:过P点作PN∥AB,
∴∠APN=∠BAP,
∵AB∥CD,
∴PN∥CD,
∴∠NPC=∠PCD,
∵∠APC=∠APN﹣∠NPC,
∴∠APC=∠BAP﹣∠PCD;
∵∠BAP=α,∠DCP=β,
∴∠APC=α﹣β
1.如图,直线MN∥PQ,点A是MN上一点,∠MAC的角平分线交PQ于点B,若∠1=20°,∠2=116°,则∠3的大小为( )
A.136° B.138° C.146° D.148°
2.如图,a∥b,∠ABD的平分线交直线a于点C,CE⊥直线c于点E,∠1=24°,则∠2的大小为( )
A.114° B.142° C.147° D.156°
3.如图,AB∥DE,那么∠BCD=( )
A.180°+∠1﹣∠2 B.∠1+∠2
C.∠2﹣∠1 D.180°+∠2﹣2∠1
4.如图,AB∥CD,则下列等式正确的是( )
A.∠1=∠2+∠3 B.∠1﹣∠2=180°﹣∠3
C.∠1﹣∠3=180°﹣∠2 D.∠1+∠2+∠3=180°
5.如图,已知AB∥DE,∠ABC=130°,∠CDE=110°,则∠BCD的度数为( )
A.50° B.60° C.70° D.80°
6.如图,已知AB∥DF,DE和AC分别平分∠CDF和∠BAE,若∠DEA=46°,∠ACD=56°,则∠CDF的度数为( )
A.42° B.43° C.44° D.45°
7.如图,直线AB∥CD,点F在直线AB上,点N在直线CD上,∠EFA=25°,∠FGH=90°,∠HMN=25°,∠CNP=30°,则∠GHM=( )
A.45° B.50° C.55° D.60°
8.如图,∠BCD=90°,AB∥DE,若∠a=40°,则∠β的大小为( )
A.40° B.50 C.130° D.140°
9.已知直线m∥n,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),并且顶点A,C分别落在直线m,n上,若∠1=38°,则∠2的度数是( )
A.20° B.22° C.28° D.38°
10.两个角的两边两两互相平行,且一个角的等于另一个角的,则这两个角中较小角的度数为 °.
11.如图,直线AB、CD被直线EF所截,AB∥CD,DG⊥BF于点G,若∠1=130°,则∠2的度数为 .
12.如图,如果AB∥CD,则角α=130°,γ=20°,则β= .
13.如图,已知AB∥DE,∠ABC=76°,∠CDE=150°,则∠BCD的度数为 °.
14.如图,已知AB∥DE,∠ABC=135°,∠CDE=70°,则∠BCD= .
15.如图,已知直线l1∥l2,∠1=30°,则∠2+∠3= .
16.如图,已知AB∥CF,CF∥DE,∠BCD=90°,则∠D﹣∠B= .
17.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=115°,∠ACF=25°,则∠FEC= 度.
18.如图,直线l1∥l2,∠α=∠β,∠1=38°,则∠2= .
19.如图,直线AB∥直线CD,线段EF∥CD,连接BF、CF.
(1)求证:∠ABF+∠DCF=∠BFC;
(2)连接BE、CE、BC,若BE平分∠ABC,BE⊥CE,求证:CE平分∠BCD;
(3)在(2)的条件下,G为EF上一点,连接BG,若∠BFC=∠BCF,∠FBG=2∠ECF,∠CBG=70°,求∠FBE的度数.
20.已知:如图,EF平分∠DEB,AC∥DE,CD∥EF,请证明:CD平分∠ACB.
21.如图,EF∥AD,∠1=∠2.
(1)若∠B=55°,求∠BDG的度数;
(2)若AD平分∠BAC,直接写出∠DGC与∠FEA的数量关系.
22.直线AB、CD被直线EF所截,AB∥CD,点P是平面内一动点.
(1)若点P在直线CD上,如图①,∠α=50°,则∠2= °.
(2)若点P在直线AB、CD之间,如图②,试猜想∠α、∠1、∠2之间的等量关系并给出证明;
(3)若点P在直线CD的下方,如图③,(2)中∠α、∠1、∠2之间的关系还成立吗?请作出判断并说明理由.
23.已知直线AB∥CD,直线EF分别交AB、CD于点A、C,CM是∠ACD的平分线,CM交AB于点H,过点A作AG⊥AC交CM于点G.
(1)如图1,点G在CH的延长线上时,若∠GAB=36°,求∠MCD的度数;
(2)如图2,点G在CH上时,试说明2∠MCD+∠GAB=90°.
24.(1)如图①,AB∥CD,∠A=43°,∠C=33°,求∠APC的度数;
(2)如图②,AB∥CD,当点P在线段BD上移动时,设∠BAP=α,∠DCP=β,写出∠APC与α,β之间的数量关系,并说明理由;
(3)在(2)的条件下,如果点P在射线DM上运动,请你直接写出∠APC与α,β之间的数量关系.
参考答案
1.解:延长QC交AB于D,
∵MN∥PQ,
∴∠2+∠MAB=180°,
∵∠2=116°,
∴∠MAB=180°﹣116°=64°,
∵AB平分∠MAC,
∴∠MAB=∠BAC=64°,
△BDQ中,∠BDQ=∠2﹣∠1=116°﹣20°=96°,
∴∠ADC=180°﹣96°=84°,
△ADC中,∠3=∠BAC+∠ADC=64°+84°=148°.
故选:D.
2.解:∵∠1=24°,CE⊥直线c于点E,
∴∠EAC=90°﹣∠1=90°﹣24°=66°,
∵a∥b,
∴∠EAC=∠ABD=66°,
∵∠ABD的平分线交直线a于点C,
∴∠CBD=,
∴∠2=180°﹣∠CBD=180°﹣33°=147°,
故选:C.
3.解:过点C作CF∥AB,如图:
∵AB∥DE,
∴AB∥DE∥CF,
∴∠BCF=∠1①,∠2+∠DCF=180°②,
∴①+②得,∠BCF+∠DCF+∠2=∠1+180°,即∠BCD=180°+∠1﹣∠2.
故选:A.
4.解:如右图所示,
∵CD∥AB,
∴∠4=∠3,
∵∠4=∠2+(180°﹣∠1),
∴∠3=∠2+(180°﹣∠1),
∴∠1﹣∠2=180°﹣∠3,
故选:B.
5.解:作DE的反向延长线交BC于M,
∵AB∥DE,∠ABC=130°,
∴∠BMD=∠ABC=130°,
∴∠CMD=180°﹣∠BMD=50°,
∵∠CDE=110°,
∴∠BCD=∠CDE﹣∠CMD=110°﹣50°=60°,
故选:B.
6.解:过点C作CN∥AB,过点E作EM∥AB,
∵FD∥AB,CN∥AB,EM∥AB,
∴AB∥CN∥EM∥FD
∴∠BAC=∠NCA,∠NCD=∠FDC,∠FDE=∠DEM,∠MEA=∠EAB.
∴∠DEA=∠FDE+∠EAB,
∠ACD=∠BAC+∠FDC.
又∵DE和AC分别平分∠CDF和∠BAE,
∴∠FDC=2∠FDE=2∠EDC,∠BAE=2∠BAC=2∠EAC
∴56°=∠BAC+2∠FDE①,
46°=∠FDE+2∠BAC②.
①+②,得3(∠BAC+∠FDE)=102°,
∴∠BAC+∠FDE=34°③.
①﹣③,得∠FDE=22°.
∴∠CDF=2∠FDE=44°.
故选:C.
7.解:延长HG交直线AB于点K,延长PM交直线AB于点S.
∵AB∥CD,
∴∠KSM=∠CNP=30°.
∵∠EFA=∠KFG=25°,∠KGF=180°﹣∠FGH=90°,
∠SMH=180°﹣∠HMN=155°,
∴∠SKH=∠KFG+∠KGF=25°+90°=115°.
∵∠SKH+∠GHM+∠SMH+∠KSM=360°,
∴∠GHM=360°﹣115°﹣155°﹣30°=60°.
故选:D.
8.解:过C作CF∥AB,
∵AB∥DE,
∴AB∥CF∥DE,
∴∠1=∠α=40°,∠2=180°﹣∠β,
∵∠BCD=90°,
∴∠1+∠2=40°+180°﹣∠β=90°,
∴∠β=130°.
故选:C.
9.解:∵∠ABC=30°,∠BAC=90°,
∴∠ACB=60°,
过C作CD∥直线m,
∵直线m∥n,
∴CD∥直线m∥直线n,
∴∠1=∠ACD,∠2=∠BCD,
∵∠1=38°,
∴∠ACD=38°,
∴∠2=∠BCD=60°﹣38°=22°,
故选:B.
10.解:∵一个角的等于另一个角的,
∴这两个角不相等,
设其中一个角的度数为x°,另一个角的度数为x=x°,
∵两个角的两边两两互相平行,
∴x+x=180,
解得:x=72,
即较小角的度数是72°,
故选:72.
11.解:∵AB∥CD,∠1=130°,
∴∠CFB=∠1=130°,
∴∠BFD=180°﹣∠CFB=180°﹣130°=50°,
∵DG⊥BF,
∴∠DGF=90°,
∴∠2=90°﹣∠BFD=90°﹣50°=40°,
故答案为40°.
12.解:如图,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠A+∠AEF=180°,∠D=∠FED,
∴∠AEF=180°﹣130°=50°,∠FED=20°,
∴∠AED=∠AEF+∠FED=50°+20°=70°.
即β=70°.
故答案为:70°.
13.解:过点C作CF∥AB,
∵AB∥DE,
∴AB∥DE∥CF,
∴∠ABC=∠BCF,∠CDE+∠DCF=180°,
∵∠ABC=76°,∠CDE=150°,
∴∠BCF=76°,∠DCF=30°,
∴∠BCD=46°,
故答案为:46.
14.解:如图,延长CB交ED的延长线于G.
∵AB∥DF,
∴∠1=∠ABC=135°,
∵∠1=∠CDG+∠C,∠CDG=180°﹣∠CDE=110°,
∴∠BCD=135°﹣110°=25°,
故答案为25°.
15.解:如图.
∵直线l1∥l2,
∴∠3+∠4=180°,
∵∠2=∠1+∠4,
∴∠3+∠4+∠2=180°+∠1+∠4,
∵∠1=30°,
∴∠2+∠3=180°+30°=210°.
故答案为210°
16.解:∵AB∥CF,
∵∠B=∠1,
∵CF∥DE,
∴∠D+∠2=180°,即∠2=180°﹣∠D,
∵∠BCD=90°,
∴∠1+∠2=90°,即∠B+180°﹣∠D=90°,
∴∠D﹣∠B=90°.
故答案为:90°.
17.解:∵AD∥BC,
∴∠ACB=180°﹣∠DAC=180°﹣115°=65°,
∵∠ACF=25°,
∴∠BCF=∠ACB﹣∠ACF=65°﹣25°=40°,
∵CE平分∠BCF,
∴∠BCE=∠BCF=×40°=20°,
∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠FEC=∠BCE=20°.故答案为:20.
18.解:延长AB交l2于点E,
∵∠α=∠β,
∴AB∥DC,
∴∠3+∠2=180°,
∵l1∥l2,
∴∠1=∠3=38°,
∴∠2=180°﹣38°=142°,故答案为:142°.
19.证明:(1)∵AB∥CD,EF∥CD,
∴AB∥EF,
∴∠ABF=∠BFE,
∵EF∥CD,
∴∠DCF=∠EFC,
∴∠BFC=∠BFE+∠EFC=∠ABF+∠DCF;
(2)∵BE⊥EC,
∴∠BEC=90°,
∴∠EBC+∠BCE=90°,
由(1)可得:∠BFC=∠ABE+∠ECD=90°,
∴∠ABE+∠ECD=∠EBC+∠BCE,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ECD=∠BCE,
∴CE平分∠BCD;
(3)设∠BCE=β,∠ECF=γ,
∵CE平分∠BCD,
∴∠DCE=∠BCE=β,
∴∠DCF=∠DCE﹣∠ECF=β﹣γ,
∴∠EFC=β﹣γ,
∵∠BFC=∠BCF,
∴∠BFC=∠BCE+∠ECF=γ+β,
∴∠ABF=∠BFE=2γ,
∵∠FBG=2∠ECF,
∴∠FBG=2γ,
∴∠ABE+∠DCE=∠BEC=90°,
∴∠ABE=90°﹣β,
∴∠GBE=∠ABE﹣∠ABF﹣∠FBG=90°﹣β﹣2γ﹣2γ,
∵BE平分∠ABC,
∴∠CBE=∠ABE=90°﹣β,
∴∠CBG=∠CBE+∠GBE,
∴70°=90°﹣β+90°﹣β﹣2γ﹣2γ,
整理得:2γ+β=55°,
∴∠FBE=∠FBG+∠GBE=2γ+90°﹣β﹣2γ﹣2γ=90°﹣(2γ+β)=35°.
20.解:∵AC∥DE,
∴∠ACD=∠CDE,
∵CD∥EF,
∴∠DCB=∠FEB,∠CDE=∠DEF,
∴∠ACD=∠DEF,
又∵EF平分∠DEB,
∴∠DEF=∠FEB,
∴∠ACD=∠DCB,
∴CD平分∠ACB.
21.解:(1)∵EF∥AD,
∴∠2=∠3,
∵∠1=∠2,
∴∠1=∠3,
∴DG∥BA,
∴∠B+∠BDG=180°,
∵∠B=55°,
∴∠BDG=125°;
(2)∠DGC+∠FEA=180°,
理由:∵AD平分∠BAC,
∴∠BAC=2∠3,
由(1)知,DG∥BA,
∴∠CGD=∠BAC,
∴∠CGD=2∠3,
∵EF∥AD,
∴∠FEA+∠3=180°,
∴∠DGC+∠FEA=180°.
22.解:①∵AB∥CD,∠α=50°
∴∠2=∠α=50°,
故答案为50;
(2)∠α=∠1+∠2.
证明:过P作PG∥AB,
∵AB∥CD,
∴PG∥AB∥CD,
∴∠2=∠EPG,∠1=∠FPG,
∵∠α=∠EPF=∠EPG+∠FPG,
∴∠α=∠1+∠2;
(3)不成立.
理由:过P作PH∥AB,
∵AB∥CD,
∴PH∥AB∥CD,
∴∠2=∠EPH,∠1=∠FPH,
∵∠α=∠EPF=∠EPH﹣∠FPH,
∴∠α=∠2﹣∠1,
故不成立.
23.解:(1)∵AG⊥AC,∠GAB=36°,
∴∠CAH=90°﹣36°=54°,
∵AB∥CD,
∴∠ACD+∠CAH=180°,
∴∠ACD=126°,
∵CM是∠ACD的平分线,
∴∠ACH=∠DCM=63°.
(2)∵∠ACH=∠DCM,
∴∠ACD=2∠MCD,
由(1)得ACD+∠CAH=180°,
∵AG⊥AC,
∴∠CAG=90°,
∴2∠MCD+90°+∠GAB=180°,
∴2∠MCD+∠GAB=90°.
24.解:(1)过P点作PE∥AB,
∴∠APE=∠A,
∵AB∥CD,
∴PE∥CD,
∴∠EPC=∠C,
∵∠APC=∠APE+∠EPC,
∴∠APC=∠A+∠C
∵∠A=43°,∠C=33°,
∴∠APC=43°+33°=76°;
(2)∠APC=α+β.
理由:过P点作PF∥AB,
∴∠APF=∠BAP,
∵AB∥CD,
∴PF∥CD,
∴∠FPC=∠PCD,
∵∠APC=∠APF+∠FPC,
∴∠APC=∠BAP+∠PCD;
∵∠BAP=α,∠DCP=β,
∴∠APC=α+β;
(3)∠APC=α﹣β.
理由:过P点作PN∥AB,
∴∠APN=∠BAP,
∵AB∥CD,
∴PN∥CD,
∴∠NPC=∠PCD,
∵∠APC=∠APN﹣∠NPC,
∴∠APC=∠BAP﹣∠PCD;
∵∠BAP=α,∠DCP=β,
∴∠APC=α﹣β
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
