虹口区2009学年度第一学期初三年级数学学科
文档属性
| 名称 | 虹口区2009学年度第一学期初三年级数学学科 |  | |
| 格式 | zip | ||
| 文件大小 | 214.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-13 21:41:52 | ||
图片预览


文档简介
虹口区2009学年度第一学期初三年级数学学科
期终教学质量监控测试卷
(满分150分,考试时间100分钟) 2010.1
考生注意:
1.本试卷含三个大题,共25题;
2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;
3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一、选择题:(本大题共6题,每题4分,满分24分)
[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上]
1.如果,那么下列各式中不成立的是( )
. ; . ; .; ..
2.在锐角中,如果各边长都扩大2倍,则的正弦值( )
.扩大2倍; .缩小2倍; .大小不变; .不能确定.
3.下列抛物线中,过原点的抛物线是( )
.; .; .; ..
4. 把抛物线向上平移3个单位,则平移后抛物线的解析式为( )
.; .; .; ..
5.如图1,已知,如果,,则的长是( )
.; .; .; ..
6.下列命题中,正确的是( )
.如果一条直线截三角形两边的延长线所得的对应线段成比例,那么这条直线一定平行于三角形的第三边;
.不同向量的单位向量的长度都相等,方向也都相同;
.一般来说,一条线段的黄金分割点有两个;
.相似三角形的中线的比等于相似比.
二、填空题:(本大题共12题,每题4分,满分48分)
[请将结果直接填入答题纸的相应位置]
7. 抛物线与轴的交点坐标是__________.
8. 如果抛物线的开口向下,那么的取值范围是_____________.
9. 已知,那么锐角的度数是_____________.
10. 在△ABC中,,, , 则的值是 .
11. 在△ABC中,,,,则的长是____________.
12. 在中,中线与中线相交于点, 若,则= .
13. 已知∽,顶点、、分别与、、对应,且,,则的度数是___________.
14. 如果两个相似三角形的面积的比等于1∶9,那么它们的对应边上的高的比等于 .
15.如图2,已知在平行四边形ABCD中,点E、F分别在线段 BD、AB上,EF∥AD,DE∶EB=2∶3,EF=9,那么BC的长为 .
16. 如图3,一辆汽车沿着坡度的斜坡向下行驶50米,则它距离地面的垂直高度下降了 米.
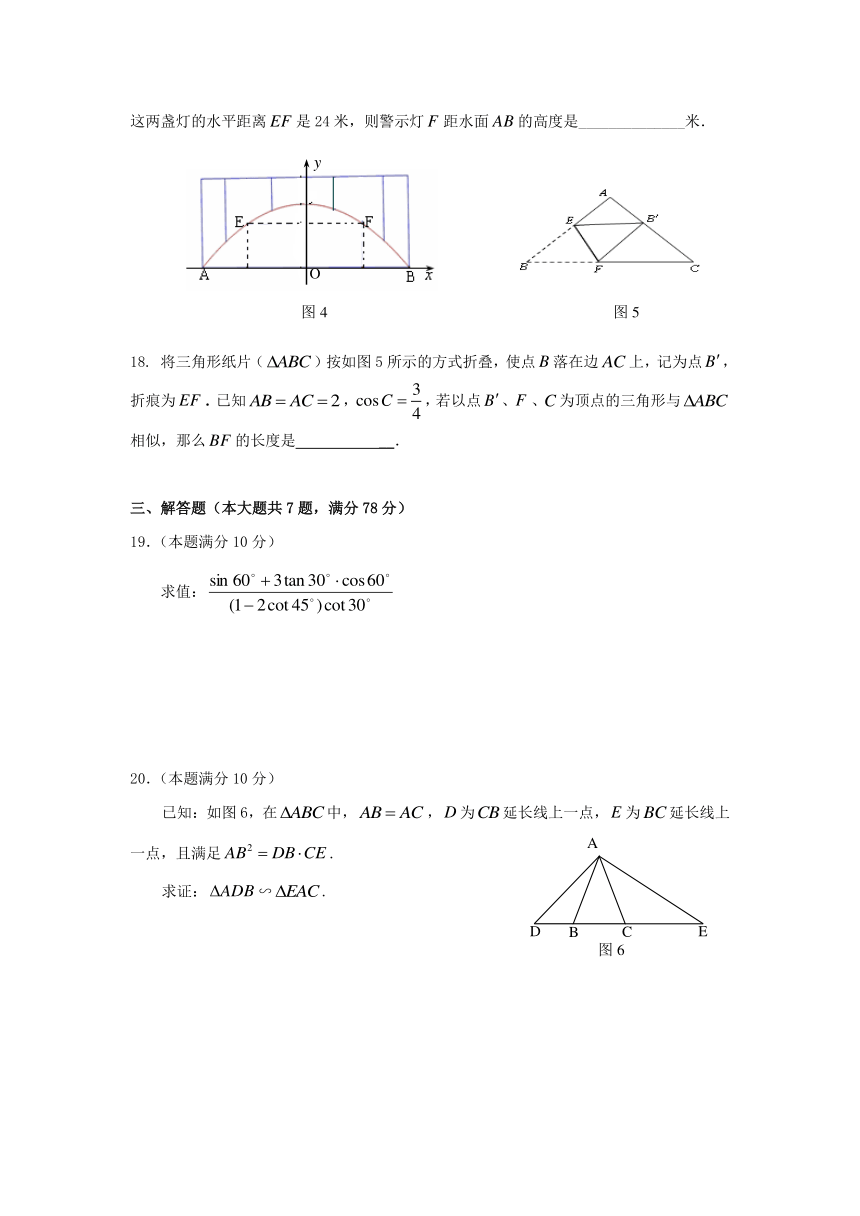
17.某抛物线型拱桥的示意图如图4,已知该抛物线的函数表达式为,为保护该桥的安全,在该抛物线上的点、处要安装两盏警示灯(点、关于轴对称),这两盏灯的水平距离是24米,则警示灯距水面的高度是______________米.
18. 将三角形纸片()按如图5所示的方式折叠,使点落在边上,记为点,折痕为.已知,,若以点、、为顶点的三角形与相似,那么的长度是 __.
三、解答题(本大题共7题,满分78分)
19.(本题满分10分)
求值:
20.(本题满分10分)
已知:如图6,在中,,为延长线上一点,为延长线上一点,且满足.
求证:∽.
21.(本题满分10分)
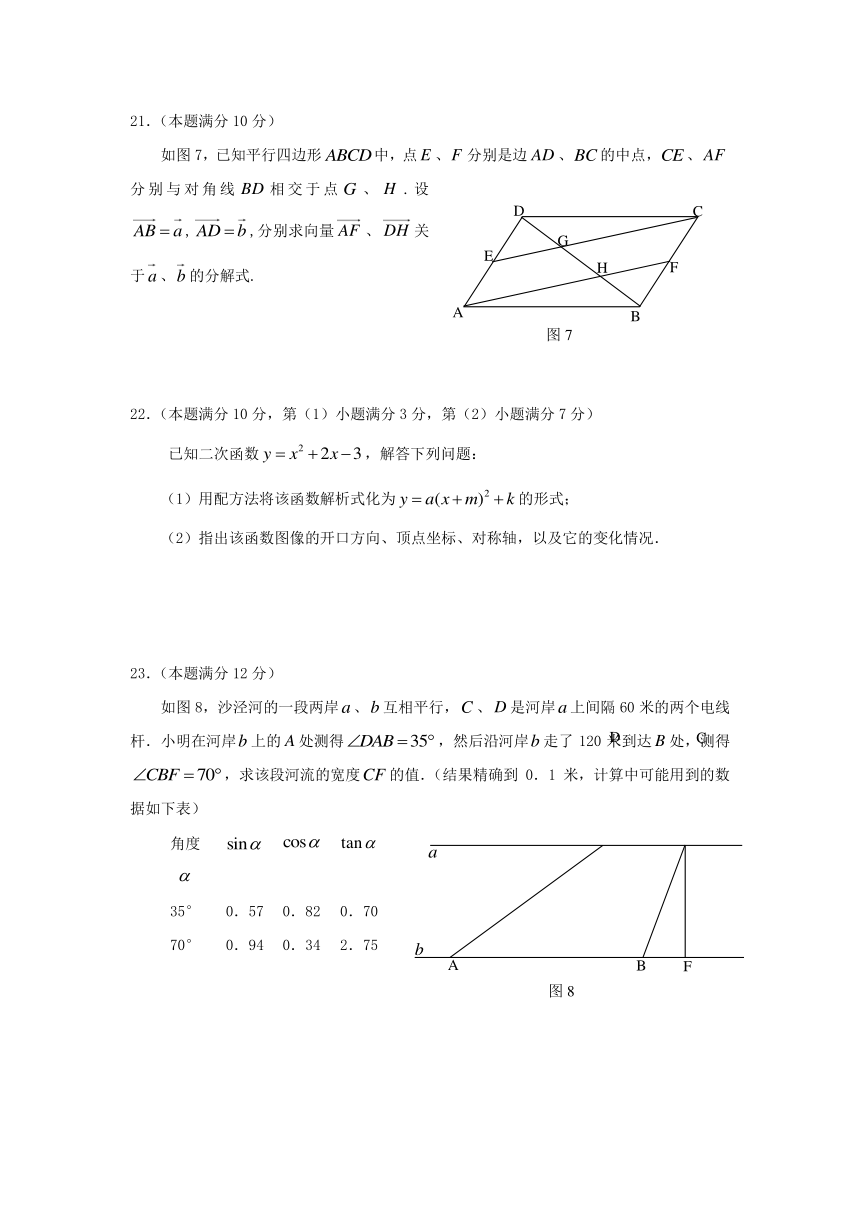
如图7,已知平行四边形中,点、分别是边、的中点,、分别与对角线相交于点、.设,,分别求向量、关于、的分解式.
22.(本题满分10分,第(1)小题满分3分,第(2)小题满分7分)
已知二次函数,解答下列问题:
(1)用配方法将该函数解析式化为的形式;
(2)指出该函数图像的开口方向、顶点坐标、对称轴,以及它的变化情况.
23.(本题满分12分)
如图8,沙泾河的一段两岸、互相平行,、是河岸上间隔60米的两个电线杆.小明在河岸上的处测得,然后沿河岸走了120米到达处,测得,求该段河流的宽度的值.(结果精确到0.1米,计算中可能用到的数据如下表)
角度
35° 0.57 0.82 0.70
70° 0.94 0.34 2.75
24.(本题满分12分,第(1)小题满分6分,第(2)小题满分3分,第(3)小题满分3分)
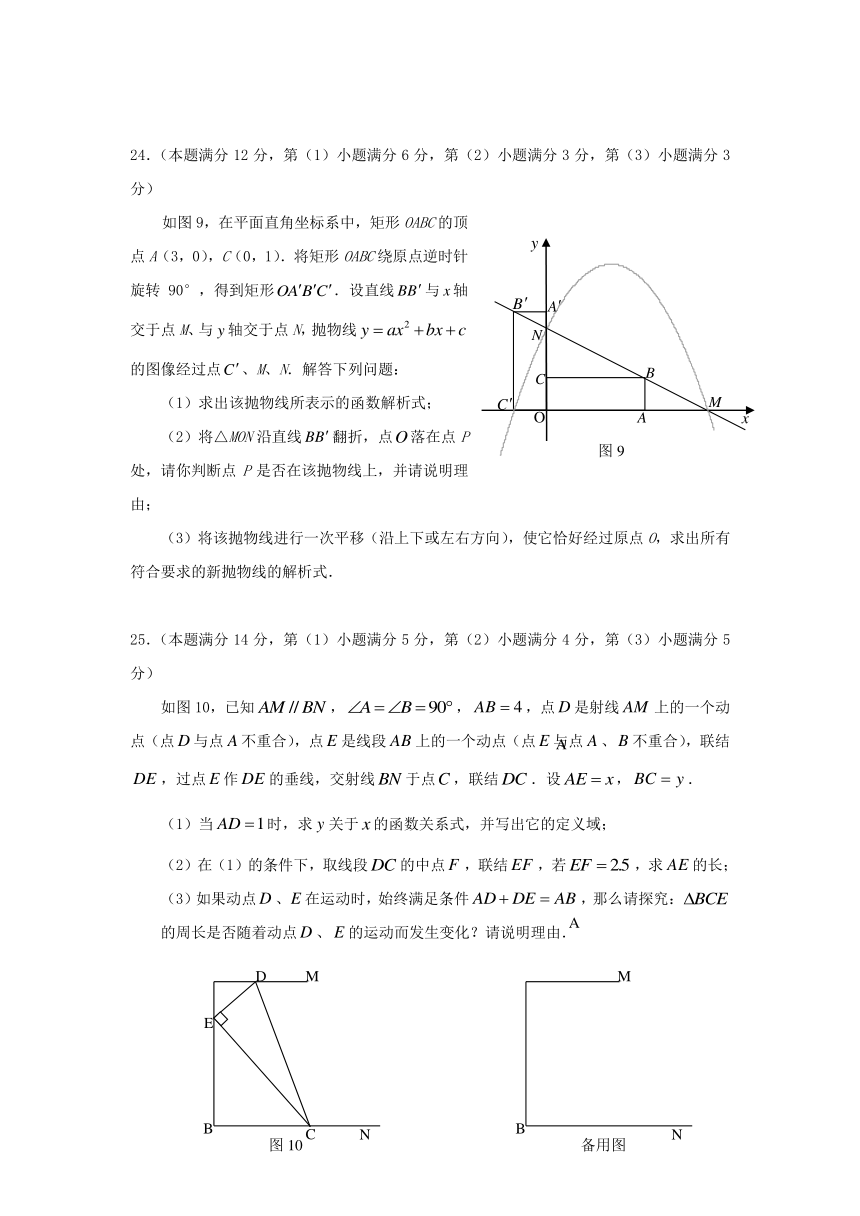
如图9,在平面直角坐标系中,矩形OABC的顶点A(3,0),C(0,1).将矩形OABC绕原点逆时针旋转90°,得到矩形.设直线与轴交于点M、与轴交于点N,抛物线的图像经过点、M、N.解答下列问题:
(1)求出该抛物线所表示的函数解析式;
(2)将△MON沿直线翻折,点落在点P处,请你判断点P是否在该抛物线上,并请说明理由;
(3)将该抛物线进行一次平移(沿上下或左右方向),使它恰好经过原点O,求出所有符合要求的新抛物线的解析式.
25.(本题满分14分,第(1)小题满分5分,第(2)小题满分4分,第(3)小题满分5分)
如图10,已知,,,点是射线上的一个动点(点与点不重合),点是线段上的一个动点(点与点、不重合),联结,过点作的垂线,交射线于点,联结.设,.
(1)当时,求关于的函数关系式,并写出它的定义域;
(2)在(1)的条件下,取线段的中点,联结,若,求的长; (3)如果动点、在运动时,始终满足条件,那么请探究:的周长是否随着动点、的运动而发生变化?请说明理由.
虹口区2009学年度第一学期初三年级数学学科
期终教学质量监控测试卷参考答案及评分建议
2010.1
说明:
1.解答只列出试题的一种或几种解法.如果考生的解法与所列解法不同,可参照解答中评分标准相应评分;
2.第一、二大题若无特别说明,每题评分只有满分或零分;
3.第三大题中各题右端所注分数,表示考生正确做对这一步应得分数;
4.评阅试卷,要坚持每题评阅到底,不能因考生解答中出现错误而中断对本题的评阅.如果考生的解答在某一步出现错误,影响后继部分而未改变本题的内容和难度,视影响的程度决定后继部分的给分,但原则上不超过后继部分应得分数的一半;
5.评分时,给分或扣分均以1分为基本单位.
一、选择题:
1.D; 2.C; 3.B; 4.D; 5.B; 6.C.
二、填空题:
7.(0, 2); 8.; 9.; 10.; 11.4; 12.2.
13. ; 14. ; 15.15; 16.25; 17. 9; 18..
三、解答题
19. ……………………………………………………………(5分)
…………………………………………………………………………(3分)
=……………………………………………………………………………(2分)
20.证明:
……………………………………………………………(3分) …………………………………………………………(2分)
……………………………………………………………………(4分)
∴∽…………………………………………………………………(1分)
21.解的边的中点,
…………………………………………………………(4分)
…………………………………………………(1分)
………………………………………………………………………(1分)
……………………………………………………(2分)
………………………………………………………(2分)
22.解:…………………………………………………………(1分)
……………………………………………………………(2分)
∴该函数图像的开口向上;顶点坐标是;对称轴是直线;图像在直线左侧部分是下降的,右侧的部分是上升的. …………(1分,2分,2分,2分)
23.解:过作, 交.(如图)………………………………………(1分)
∴ 四边形是平行四边形…………(2分)
……………………………………………………………………(4分)
…………………(4分)
答:河流的宽度的值约为56.4米. …………………………………………………(1分)
24.解(1) 可以求出点……………………………(3分)
…………………………………………………………………(2分)
∴所求抛物线的解析式为……………………………………(1分)
(2)不存在,理由如下:
可求出点……………………………………………………………………(2分)
∴点P不在该抛物线上………………………………………………………………(1分)
(3)
∴ 所求的抛物线的解析式为:
……………………………………………(1分)
……………………………………………(1分)
…………………………………………(1分)
25.解:(1)可证∽……………………………………………………(1分)
…………………………………………………………………………(1分)
……………………(2分,1分)
……………………………………(1分)
过点作, 则
………………………………………………………(1分)
………………………………………………………………………(1分)
解得:
………………………………………………………………………………(1分)
(3) 的周长不变,理由如下:
,…………………………………(1分)
设,则,
由(1)知:∽
…………………………………………………(2分)
………………………………………(1分)
的周长不变.……………………………………………………………(1分)
A
B
C
E
图1
D
F
D
A
B
C
F
E
图2
图3
O
图5
图4
A
B
C
D
E
图6
A
B
C
D
E
F
G
H
图7
D
C
A
B
F
图8
A
B
O
C
N
M
x
图9
A
B
M
N
备用图
A
B
M
N
D
E
C
图10
期终教学质量监控测试卷
(满分150分,考试时间100分钟) 2010.1
考生注意:
1.本试卷含三个大题,共25题;
2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效;
3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤.
一、选择题:(本大题共6题,每题4分,满分24分)
[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上]
1.如果,那么下列各式中不成立的是( )
. ; . ; .; ..
2.在锐角中,如果各边长都扩大2倍,则的正弦值( )
.扩大2倍; .缩小2倍; .大小不变; .不能确定.
3.下列抛物线中,过原点的抛物线是( )
.; .; .; ..
4. 把抛物线向上平移3个单位,则平移后抛物线的解析式为( )
.; .; .; ..
5.如图1,已知,如果,,则的长是( )
.; .; .; ..
6.下列命题中,正确的是( )
.如果一条直线截三角形两边的延长线所得的对应线段成比例,那么这条直线一定平行于三角形的第三边;
.不同向量的单位向量的长度都相等,方向也都相同;
.一般来说,一条线段的黄金分割点有两个;
.相似三角形的中线的比等于相似比.
二、填空题:(本大题共12题,每题4分,满分48分)
[请将结果直接填入答题纸的相应位置]
7. 抛物线与轴的交点坐标是__________.
8. 如果抛物线的开口向下,那么的取值范围是_____________.
9. 已知,那么锐角的度数是_____________.
10. 在△ABC中,,, , 则的值是 .
11. 在△ABC中,,,,则的长是____________.
12. 在中,中线与中线相交于点, 若,则= .
13. 已知∽,顶点、、分别与、、对应,且,,则的度数是___________.
14. 如果两个相似三角形的面积的比等于1∶9,那么它们的对应边上的高的比等于 .
15.如图2,已知在平行四边形ABCD中,点E、F分别在线段 BD、AB上,EF∥AD,DE∶EB=2∶3,EF=9,那么BC的长为 .
16. 如图3,一辆汽车沿着坡度的斜坡向下行驶50米,则它距离地面的垂直高度下降了 米.
17.某抛物线型拱桥的示意图如图4,已知该抛物线的函数表达式为,为保护该桥的安全,在该抛物线上的点、处要安装两盏警示灯(点、关于轴对称),这两盏灯的水平距离是24米,则警示灯距水面的高度是______________米.
18. 将三角形纸片()按如图5所示的方式折叠,使点落在边上,记为点,折痕为.已知,,若以点、、为顶点的三角形与相似,那么的长度是 __.
三、解答题(本大题共7题,满分78分)
19.(本题满分10分)
求值:
20.(本题满分10分)
已知:如图6,在中,,为延长线上一点,为延长线上一点,且满足.
求证:∽.
21.(本题满分10分)
如图7,已知平行四边形中,点、分别是边、的中点,、分别与对角线相交于点、.设,,分别求向量、关于、的分解式.
22.(本题满分10分,第(1)小题满分3分,第(2)小题满分7分)
已知二次函数,解答下列问题:
(1)用配方法将该函数解析式化为的形式;
(2)指出该函数图像的开口方向、顶点坐标、对称轴,以及它的变化情况.
23.(本题满分12分)
如图8,沙泾河的一段两岸、互相平行,、是河岸上间隔60米的两个电线杆.小明在河岸上的处测得,然后沿河岸走了120米到达处,测得,求该段河流的宽度的值.(结果精确到0.1米,计算中可能用到的数据如下表)
角度
35° 0.57 0.82 0.70
70° 0.94 0.34 2.75
24.(本题满分12分,第(1)小题满分6分,第(2)小题满分3分,第(3)小题满分3分)
如图9,在平面直角坐标系中,矩形OABC的顶点A(3,0),C(0,1).将矩形OABC绕原点逆时针旋转90°,得到矩形.设直线与轴交于点M、与轴交于点N,抛物线的图像经过点、M、N.解答下列问题:
(1)求出该抛物线所表示的函数解析式;
(2)将△MON沿直线翻折,点落在点P处,请你判断点P是否在该抛物线上,并请说明理由;
(3)将该抛物线进行一次平移(沿上下或左右方向),使它恰好经过原点O,求出所有符合要求的新抛物线的解析式.
25.(本题满分14分,第(1)小题满分5分,第(2)小题满分4分,第(3)小题满分5分)
如图10,已知,,,点是射线上的一个动点(点与点不重合),点是线段上的一个动点(点与点、不重合),联结,过点作的垂线,交射线于点,联结.设,.
(1)当时,求关于的函数关系式,并写出它的定义域;
(2)在(1)的条件下,取线段的中点,联结,若,求的长; (3)如果动点、在运动时,始终满足条件,那么请探究:的周长是否随着动点、的运动而发生变化?请说明理由.
虹口区2009学年度第一学期初三年级数学学科
期终教学质量监控测试卷参考答案及评分建议
2010.1
说明:
1.解答只列出试题的一种或几种解法.如果考生的解法与所列解法不同,可参照解答中评分标准相应评分;
2.第一、二大题若无特别说明,每题评分只有满分或零分;
3.第三大题中各题右端所注分数,表示考生正确做对这一步应得分数;
4.评阅试卷,要坚持每题评阅到底,不能因考生解答中出现错误而中断对本题的评阅.如果考生的解答在某一步出现错误,影响后继部分而未改变本题的内容和难度,视影响的程度决定后继部分的给分,但原则上不超过后继部分应得分数的一半;
5.评分时,给分或扣分均以1分为基本单位.
一、选择题:
1.D; 2.C; 3.B; 4.D; 5.B; 6.C.
二、填空题:
7.(0, 2); 8.; 9.; 10.; 11.4; 12.2.
13. ; 14. ; 15.15; 16.25; 17. 9; 18..
三、解答题
19. ……………………………………………………………(5分)
…………………………………………………………………………(3分)
=……………………………………………………………………………(2分)
20.证明:
……………………………………………………………(3分) …………………………………………………………(2分)
……………………………………………………………………(4分)
∴∽…………………………………………………………………(1分)
21.解的边的中点,
…………………………………………………………(4分)
…………………………………………………(1分)
………………………………………………………………………(1分)
……………………………………………………(2分)
………………………………………………………(2分)
22.解:…………………………………………………………(1分)
……………………………………………………………(2分)
∴该函数图像的开口向上;顶点坐标是;对称轴是直线;图像在直线左侧部分是下降的,右侧的部分是上升的. …………(1分,2分,2分,2分)
23.解:过作, 交.(如图)………………………………………(1分)
∴ 四边形是平行四边形…………(2分)
……………………………………………………………………(4分)
…………………(4分)
答:河流的宽度的值约为56.4米. …………………………………………………(1分)
24.解(1) 可以求出点……………………………(3分)
…………………………………………………………………(2分)
∴所求抛物线的解析式为……………………………………(1分)
(2)不存在,理由如下:
可求出点……………………………………………………………………(2分)
∴点P不在该抛物线上………………………………………………………………(1分)
(3)
∴ 所求的抛物线的解析式为:
……………………………………………(1分)
……………………………………………(1分)
…………………………………………(1分)
25.解:(1)可证∽……………………………………………………(1分)
…………………………………………………………………………(1分)
……………………(2分,1分)
……………………………………(1分)
过点作, 则
………………………………………………………(1分)
………………………………………………………………………(1分)
解得:
………………………………………………………………………………(1分)
(3) 的周长不变,理由如下:
,…………………………………(1分)
设,则,
由(1)知:∽
…………………………………………………(2分)
………………………………………(1分)
的周长不变.……………………………………………………………(1分)
A
B
C
E
图1
D
F
D
A
B
C
F
E
图2
图3
O
图5
图4
A
B
C
D
E
图6
A
B
C
D
E
F
G
H
图7
D
C
A
B
F
图8
A
B
O
C
N
M
x
图9
A
B
M
N
备用图
A
B
M
N
D
E
C
图10
