黄浦区2009学年度第一学期期终基础学业测评
文档属性
| 名称 | 黄浦区2009学年度第一学期期终基础学业测评 |

|
|
| 格式 | zip | ||
| 文件大小 | 112.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-13 00:00:00 | ||
图片预览



文档简介
黄浦区2009学年度第一学期期终基础学业测评
初三数学试卷
(完卷时间:100分钟,满分:150分) 2010年1月20日
一、选择题【每题列出的四个选项中,有且只有一个是正确的】(本大题共6题,每题4分,满分24分)
1、三角形的重心是
(A)三角形三条角平分线的交点; (B)三角形三条中线的交点;
(C)三角形三条高所在直线的交点; (D)三角形三条边的垂直平分线的交点.
2、如图,在梯形ABCD中,E、F分别为腰AD、BC的中点,若,则向量可表示为
(A); (B); (C); (D).
(第2题) (第3题)
3、如图,在△ABC中,,则的值是
(A); (B); (C); (D)以上都不是.
4、若方程的两个实数根为、,则积为
(A); (B); (C) ; (D).
5、下列各组图形中,一定相似的是
(A)两个矩形;(B)两个菱形;(C)两个正方形;(D)两个等腰梯形.
6、将二次函数的图像沿轴方向向上平移1个单位,则所得到图像的函数解析式为
(A); (B) ;
(C); (D).
二、填空题(本大题共12题,每题4分,满分48分)
7、若∶∶=2∶3∶4,且,则____________.
8、已知单位向量,若向量与的方向相同,且长度为4,则向量=___________.(用单位向量表示)
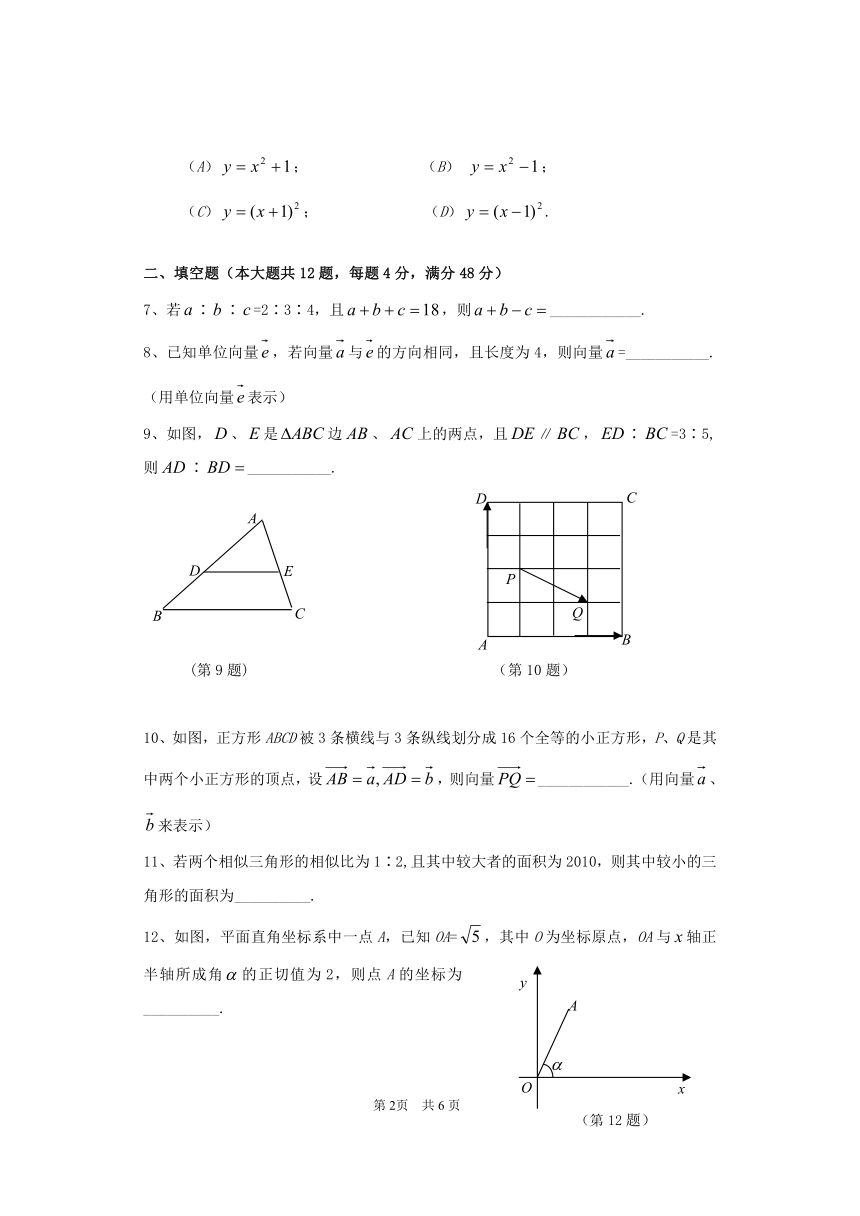
9、如图,、是边、上的两点,且∥,∶=3∶5,则∶___________.
(第9题) (第10题)
10、如图,正方形ABCD被3条横线与3条纵线划分成16个全等的小正方形,P、Q是其中两个小正方形的顶点,设,则向量____________.(用向量、来表示)
11、若两个相似三角形的相似比为1∶2,且其中较大者的面积为2010,则其中较小的三角形的面积为__________.
12、如图,平面直角坐标系中一点A,已知OA=,其中O为坐标原点,OA与轴正半轴所成角的正切值为2,则点A的坐标为__________.
13、计算:__________.
14、在平面直角坐标系中,抛物线的顶点坐标是__________.
15、一个矩形的周长为20,设其一边的长为,面积为S,则S关于的函数解析式是________.(请注明定义域)
16、若点在二次函数的图像上,则的值为__________.
17、如图,在中,是边的中点,过点O的直线将分割成两个部分,若其中的一个部分与相似,则满足条件的直线共有___________条.
(第17题) (第18题)
18、如图,在中,AB=AC,BD、CE分别为两腰上的中线,且BD⊥CE,则__________.
三、解答题(本大题共7题,满分78分)
19、(本题10分)已知关于的一元二次方程有两个实数根.
(1)试求的取值范围;
(2)若此方程的两个实数根、,满足,试求的值.
20、(本题10分)已知二次函数的图像经过点和.
(1)试求此函数的解析式;
(2)试问:将此函数的图像沿轴方向平移(向上或向下)多少个单位可以使其图像经过坐标原点?
21、(本题10分)如图,在中,是边AB上一点,且.
(1)试求的值;
(2)试求△BCD的面积.
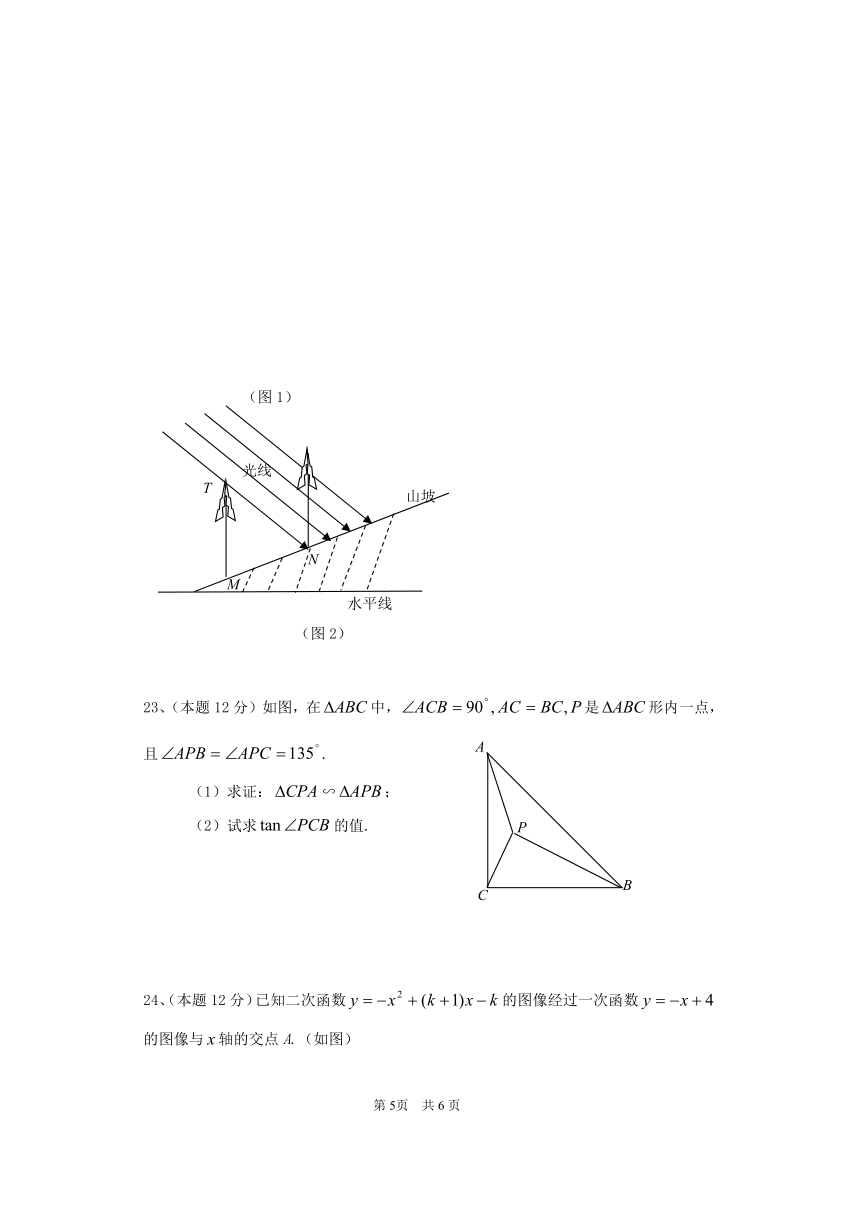
22、(本题10分)林场工作人员王护林要在一个坡度为5∶12的山坡上种植水杉树,他想根据水杉的树高与光照情况来确定植树的间距.他决定在冬至日(北半球太阳最偏南),去测量一棵成年水杉树,测得其在水平地面上的影长AB=16米,测得光线与水平地面夹角为,已知.(如图1)
(1)请根据测得的数据求出这棵成年水杉树的高度(即AT的长);
(2)如图2,他以这棵成年水杉树的高度为标准,以冬至日阳光照射时前排的树影不遮挡到后排的树为基本要求,那么他在该山坡上种植水杉树的间距(指MN的长)至少多少米?(精确到米)
(图1)
(图2)
23、(本题12分)如图,在中,是形内一点,且.
(1)求证:∽;
(2)试求的值.
24、(本题12分)已知二次函数的图像经过一次函数的图像与轴的交点A.(如图)
(1)求二次函数的解析式;
(2)求一次函数与二次函数图像的另一个交点B的坐标;
(3)若二次函数图像与轴交于点,平行于轴的直线将四边形的面积分成1∶2的两部分,则直线截四边形所得的线段的长是多少?(直接写出结果)
25、(本题14分)在梯形ABCD中,AD∥BC,.(如图1)
(1)试求的度数;
(2)若E、F分别为边AD、CD上的两个动点(不与端点A、D、C重合),且始终保持,与交于点.(如图2)
①求证:∽;
②试判断的形状(从边、角两个方面考虑),并加以说明;
③设,试求关于的函数解析式,并写出定义域.
(图1)
(图2)
2009年黄浦区初三第一学期期末考试参考答案与评分标准
一、选择题
1、B; 2、B; 3、D; 4、A; 5、C; 6、A.
二、填空题
7、2; 8、; 9、3∶2; 10、;
11、; 12、; 13、3; 14、;
15、 (0<<10); 16、12; 17、3; 18、3.
三、解答题
19、解:(1)∵方程有实数根,
∴,--------------------------(2分)
解得.-------------------------------------(2分)
(2)由根与系数关系知:,-------------(2分)
又,化简代入得,-----------(2分)
解得,---------------------------------------(1分)
经检验是方程的根且使原方程有实数根,
∴.---------------------------------------(1分)
20、解:(1)由条件得,--------------------------(3分)
解得,--------------------------------------(3分)
∴解析式为.----------------------------(1分)
(2)向下3个单位. ------------------------------------(3分)
21、解:(1)作,垂足为,------------------------(1分)
∵,
∴,------------------------------(1分)
在中,,----------------(2分)
∴.---------------------------------(1分)
(2)作,垂足为,
在中, ,令,-----------(1分)
则,---------------------(1分)
又在中,,
则,-------------------------(1分)
于是,即,
解得,------------------------------------(1分)
∴.-------------------------(1分)
22、解:(1)在中,,
令,----------(1分)
则,即,---------------------(1分)
解得,---------------------------------(1分)
∴.---------------------------------(1分)
答:这棵成年水杉树的高度为12米. -------------------(1分)
(2)作,垂足为,
在中, ,令,---(1分)
则,-------------------(1分)
又在中,,
∴,,---------(1分)
由,
解得,-------------------------------------(1分)
∴≈11.2. -------------(1分)
答:在该山坡上种植水杉树的间距至少11.2米.
23、解:(1)∵在中,
∴,即,----(1分)
又在中,,
∴,-----------------(1分)
∴,------------------------(1分)
又,--------------------(1分)
∴∽.----------------------(2分)
(2)∵是等腰直角三角形,
∴,----------------------(1分)
又∵∽,
∴,-------------------(2分)
令,则,-----------(1分)
又在中,,(1分)
∴.------------------(1分)
24、解:(1)由,得,------------------------(1分)
又二次函数图像经过点,
则,----------------------(1分)
解得,------------------------------------(1分)
所以二次函数解析式为.--------------(1分)
(2)由,----------------------------(2分)
解得,,--------------------(2分)
所以点的坐标为(2,2). --------------------(1分)
(3)3或.-----------------------------------(3分)
25、解:(1)作,垂足为,
在四边形中,AD∥BC,,
则四边形为正方形,-----------------------(1分)
又在中,,---------------------------------------------(1分)
∴.-----------------(1分)
(2)①∵四边形为正方形,
∴,,-------------------(1分)
又∵,
∴-------------------------------(1分)
又∵,-------------------------(1分)
∴∽.----------------------------(1分)
②是等腰直角三角形,-----------------------(1分)
∵∽,
∴,-------------------------------(1分)
又∵,
∴∽,---------------------------(1分)
又在中,,为等腰直角三角形,---(1分)
∴是等腰直角三角形.
③延长交的延长线于点,
易知,
∵∽,
∴,
则,
∴,
又∵,
∴,--------------------------(1分)
∵,
∴,(0<<1). -------------(2分)
C
B
A
F
E
D
C
B
A
Q
P
D
C
B
A
E
D
C
B
A
x
A
y
O
(第12题)
D
C
B
G
A
E
O
C
B
A
l
D
C
B
A
T
B
A
光线
水平线
N
M
光线
水平线
山坡
T
P
C
B
A
O
C
B
A
y
x
D
B
C
D
A
B
C
D
P
E
F
A
PAGE
第1页 共6页
初三数学试卷
(完卷时间:100分钟,满分:150分) 2010年1月20日
一、选择题【每题列出的四个选项中,有且只有一个是正确的】(本大题共6题,每题4分,满分24分)
1、三角形的重心是
(A)三角形三条角平分线的交点; (B)三角形三条中线的交点;
(C)三角形三条高所在直线的交点; (D)三角形三条边的垂直平分线的交点.
2、如图,在梯形ABCD中,E、F分别为腰AD、BC的中点,若,则向量可表示为
(A); (B); (C); (D).
(第2题) (第3题)
3、如图,在△ABC中,,则的值是
(A); (B); (C); (D)以上都不是.
4、若方程的两个实数根为、,则积为
(A); (B); (C) ; (D).
5、下列各组图形中,一定相似的是
(A)两个矩形;(B)两个菱形;(C)两个正方形;(D)两个等腰梯形.
6、将二次函数的图像沿轴方向向上平移1个单位,则所得到图像的函数解析式为
(A); (B) ;
(C); (D).
二、填空题(本大题共12题,每题4分,满分48分)
7、若∶∶=2∶3∶4,且,则____________.
8、已知单位向量,若向量与的方向相同,且长度为4,则向量=___________.(用单位向量表示)
9、如图,、是边、上的两点,且∥,∶=3∶5,则∶___________.
(第9题) (第10题)
10、如图,正方形ABCD被3条横线与3条纵线划分成16个全等的小正方形,P、Q是其中两个小正方形的顶点,设,则向量____________.(用向量、来表示)
11、若两个相似三角形的相似比为1∶2,且其中较大者的面积为2010,则其中较小的三角形的面积为__________.
12、如图,平面直角坐标系中一点A,已知OA=,其中O为坐标原点,OA与轴正半轴所成角的正切值为2,则点A的坐标为__________.
13、计算:__________.
14、在平面直角坐标系中,抛物线的顶点坐标是__________.
15、一个矩形的周长为20,设其一边的长为,面积为S,则S关于的函数解析式是________.(请注明定义域)
16、若点在二次函数的图像上,则的值为__________.
17、如图,在中,是边的中点,过点O的直线将分割成两个部分,若其中的一个部分与相似,则满足条件的直线共有___________条.
(第17题) (第18题)
18、如图,在中,AB=AC,BD、CE分别为两腰上的中线,且BD⊥CE,则__________.
三、解答题(本大题共7题,满分78分)
19、(本题10分)已知关于的一元二次方程有两个实数根.
(1)试求的取值范围;
(2)若此方程的两个实数根、,满足,试求的值.
20、(本题10分)已知二次函数的图像经过点和.
(1)试求此函数的解析式;
(2)试问:将此函数的图像沿轴方向平移(向上或向下)多少个单位可以使其图像经过坐标原点?
21、(本题10分)如图,在中,是边AB上一点,且.
(1)试求的值;
(2)试求△BCD的面积.
22、(本题10分)林场工作人员王护林要在一个坡度为5∶12的山坡上种植水杉树,他想根据水杉的树高与光照情况来确定植树的间距.他决定在冬至日(北半球太阳最偏南),去测量一棵成年水杉树,测得其在水平地面上的影长AB=16米,测得光线与水平地面夹角为,已知.(如图1)
(1)请根据测得的数据求出这棵成年水杉树的高度(即AT的长);
(2)如图2,他以这棵成年水杉树的高度为标准,以冬至日阳光照射时前排的树影不遮挡到后排的树为基本要求,那么他在该山坡上种植水杉树的间距(指MN的长)至少多少米?(精确到米)
(图1)
(图2)
23、(本题12分)如图,在中,是形内一点,且.
(1)求证:∽;
(2)试求的值.
24、(本题12分)已知二次函数的图像经过一次函数的图像与轴的交点A.(如图)
(1)求二次函数的解析式;
(2)求一次函数与二次函数图像的另一个交点B的坐标;
(3)若二次函数图像与轴交于点,平行于轴的直线将四边形的面积分成1∶2的两部分,则直线截四边形所得的线段的长是多少?(直接写出结果)
25、(本题14分)在梯形ABCD中,AD∥BC,.(如图1)
(1)试求的度数;
(2)若E、F分别为边AD、CD上的两个动点(不与端点A、D、C重合),且始终保持,与交于点.(如图2)
①求证:∽;
②试判断的形状(从边、角两个方面考虑),并加以说明;
③设,试求关于的函数解析式,并写出定义域.
(图1)
(图2)
2009年黄浦区初三第一学期期末考试参考答案与评分标准
一、选择题
1、B; 2、B; 3、D; 4、A; 5、C; 6、A.
二、填空题
7、2; 8、; 9、3∶2; 10、;
11、; 12、; 13、3; 14、;
15、 (0<<10); 16、12; 17、3; 18、3.
三、解答题
19、解:(1)∵方程有实数根,
∴,--------------------------(2分)
解得.-------------------------------------(2分)
(2)由根与系数关系知:,-------------(2分)
又,化简代入得,-----------(2分)
解得,---------------------------------------(1分)
经检验是方程的根且使原方程有实数根,
∴.---------------------------------------(1分)
20、解:(1)由条件得,--------------------------(3分)
解得,--------------------------------------(3分)
∴解析式为.----------------------------(1分)
(2)向下3个单位. ------------------------------------(3分)
21、解:(1)作,垂足为,------------------------(1分)
∵,
∴,------------------------------(1分)
在中,,----------------(2分)
∴.---------------------------------(1分)
(2)作,垂足为,
在中, ,令,-----------(1分)
则,---------------------(1分)
又在中,,
则,-------------------------(1分)
于是,即,
解得,------------------------------------(1分)
∴.-------------------------(1分)
22、解:(1)在中,,
令,----------(1分)
则,即,---------------------(1分)
解得,---------------------------------(1分)
∴.---------------------------------(1分)
答:这棵成年水杉树的高度为12米. -------------------(1分)
(2)作,垂足为,
在中, ,令,---(1分)
则,-------------------(1分)
又在中,,
∴,,---------(1分)
由,
解得,-------------------------------------(1分)
∴≈11.2. -------------(1分)
答:在该山坡上种植水杉树的间距至少11.2米.
23、解:(1)∵在中,
∴,即,----(1分)
又在中,,
∴,-----------------(1分)
∴,------------------------(1分)
又,--------------------(1分)
∴∽.----------------------(2分)
(2)∵是等腰直角三角形,
∴,----------------------(1分)
又∵∽,
∴,-------------------(2分)
令,则,-----------(1分)
又在中,,(1分)
∴.------------------(1分)
24、解:(1)由,得,------------------------(1分)
又二次函数图像经过点,
则,----------------------(1分)
解得,------------------------------------(1分)
所以二次函数解析式为.--------------(1分)
(2)由,----------------------------(2分)
解得,,--------------------(2分)
所以点的坐标为(2,2). --------------------(1分)
(3)3或.-----------------------------------(3分)
25、解:(1)作,垂足为,
在四边形中,AD∥BC,,
则四边形为正方形,-----------------------(1分)
又在中,,---------------------------------------------(1分)
∴.-----------------(1分)
(2)①∵四边形为正方形,
∴,,-------------------(1分)
又∵,
∴-------------------------------(1分)
又∵,-------------------------(1分)
∴∽.----------------------------(1分)
②是等腰直角三角形,-----------------------(1分)
∵∽,
∴,-------------------------------(1分)
又∵,
∴∽,---------------------------(1分)
又在中,,为等腰直角三角形,---(1分)
∴是等腰直角三角形.
③延长交的延长线于点,
易知,
∵∽,
∴,
则,
∴,
又∵,
∴,--------------------------(1分)
∵,
∴,(0<<1). -------------(2分)
C
B
A
F
E
D
C
B
A
Q
P
D
C
B
A
E
D
C
B
A
x
A
y
O
(第12题)
D
C
B
G
A
E
O
C
B
A
l
D
C
B
A
T
B
A
光线
水平线
N
M
光线
水平线
山坡
T
P
C
B
A
O
C
B
A
y
x
D
B
C
D
A
B
C
D
P
E
F
A
PAGE
第1页 共6页
