25.1.1 随机事件
图片预览








文档简介
(共39张PPT)
生活是数学的源泉.
探索是数学的生命线.
概率论的产生和发展
概率论产生于十七世纪,本来是由保险事业的发展而产生的,但是来自于赌博者的请求,却是数学家们思考概率论问题的源泉。
传说早在1654年,有一个赌徒梅累向当时的数学家帕斯卡提出一个使他苦恼了很久的问题:“两个赌徒相约赌若干局,谁先赢 3局就算赢,全部赌本就归谁。但是当其中一个人赢了 2局,另一个人赢了1局的时候,由于某种原因,赌博终止了。问:赌本应该如何分法才合理?”
帕斯卡是17世纪著名的数学家,但这个问题却让他苦苦思索了三年,三年后,也就是1657年,荷兰著名的数学家惠更斯企图自己解决这一问题,结果写成了《论赌博中的计算》一书,这就是概率论最早的一部著作。
近几十年来,随着科技的蓬勃发展,概率论大量应用到国民经济、工农业生产及各学科领域。许多兴起的应用数学,如信息论、对策论、排队论、控制论等,都是以概率论作为基础的。
25.1 随机事件与概率
25.1.1 随机事件
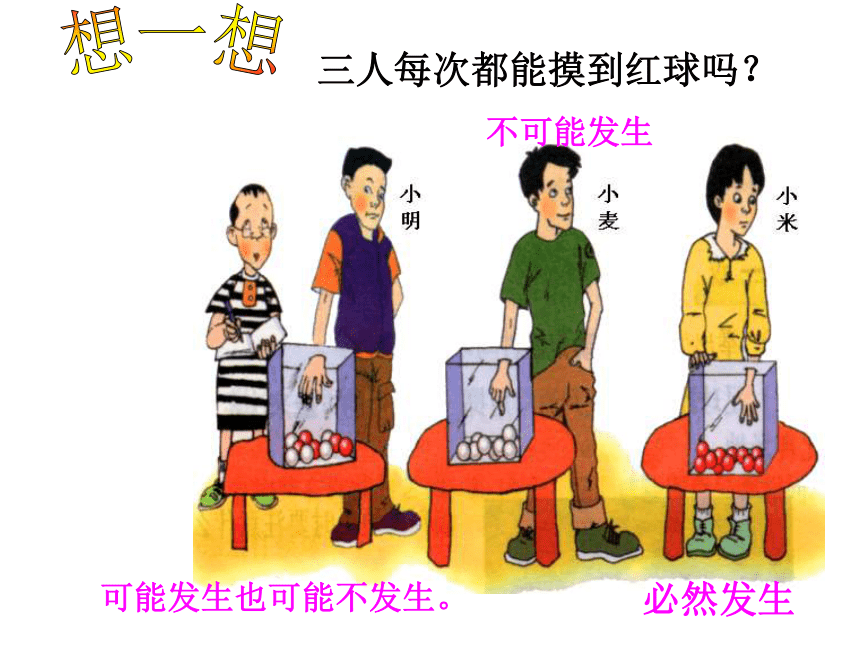
小明从盒中任意摸出一球,一定能摸到红球吗?
不一定.
小麦和小米也能摸到红球吗?
一定摸不到红球。
一定摸到红球。
三人每次都能摸到红球吗?
可能发生也可能不发生。
必然发生
不可能发生
问题1:5名同学参加演讲比赛,以抽签方式决定每个人的出场顺序。签筒中有5根形状、大小完全相同的纸签,上面分别标有出场的序号1、2、3、4、5,小军首先抽签,他在看不到纸签上数字的情况下从筒中随机(任意)地取一根纸签,请考虑以下问题:
⑴抽到的序号有几种可能情况?
⑵抽到的序号小于6吗?
⑶抽到的序号会是0吗?
⑷抽到的序号是1吗?
每次抽签的结果有5种,每次不一定相同,可能是1、2、3、4、5中的任意一张.
只能是这5张中的一张,序号肯定是小于6的.
抽到序号不会是0,只会大于0.
抽到的序号可能是1,也可能不是1,但事先无法确定.
小伟掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,请考虑以下问题:掷一次骰子,在骰子向上的一面上,
(1)可能出现哪些点数?
(2)出现的点数大于0吗?
(3)出现在的点数会是7吗?
(4)出现的点数会是4吗?
问题2
可能是1、2、3、4、5、6中的任意一个点数.
出现的点数一定大于0.
抽到序号不可能是7.
抽到的序号可能是4,也可能不是4,但事先无法确定.
(1)生活中,有些事情我们事先能肯定它一定会发生,你能举出例子吗?
(2)生活中,有些事情我们事先能肯定它一定不会发生,你能举出例子吗?
(3)生活中,有些事情有时会发生,有时不会发生,你能举出例子吗?
试分析:“从一堆牌中任意抽一张抽到红牌”这一事件的发生情况
可能发生, 也可能不发生
必然发生
必然不会发生
必然会发生。
必然不会发生。
可能会发生,也可能不会发生。
1、在地球上,太阳每天从东方升起。
2、有一匹马奔跑的速度是70千米/秒。
3、明天,我买一注体育彩票,得500万大奖。
下列事件中哪些必然会发生,哪些必然不会发生,哪些可能会也可能不会发生?
6、2012年的中考,饶平县所城镇龙湾慈云中学15人考上饶平二中。
可能会发生,也可能不会发生。
5、掷一枚均匀的硬币,正面朝上。
可能会发生,也可能不会发生。
4、用长为3cm、4cm、7cm的三条线段首尾顺次连结,构成一个三角形。
必然不会发生。
在一定条件下:
必然会发生的事件称为必然事件;
必然不会发生的事件称为不可能事件;
可能会发生,也可能不发生的事件称为随机事件.
随机事件
随机事件
抛掷一枚硬币,正面向上。
木柴燃烧产生能量
明天地球还会转动
煮熟的鸭子,飞了。
太阳从西方升起
必然事件
必然事件
不可能事件
不可能事件
从一副牌中抽出黑桃K
3.篮球队员在罚球线上投篮一次,未投中。
4.度量三角形的内角和,结果是360°。
5.掷一次骰子,向上的一面是6点。
6.367人中至少有2个人的生日一样.
7.1+(-3)>-1。
巩固练习
必然事件
不可能事件
随机事件
随机事件
不可能事件
1.水温达到100摄氏度, 水就沸腾.
必然事件
2.汽车经过城市中某一有交通信号灯的路口,遇到红灯;
随机事件
8.某射击运动员射击一次,命中靶心。
随机事件
2011年11月28日 晴
早上,我迟到了。于是就急忙去学校上学,可是在楼梯上遇到了班主任,她批评了我一顿。我想我真不走运,她经常在办公室的啊,今天我真倒霉。我明天不能再迟到了,不然明天早上我将在楼梯上遇到班主任。
中午放学回家,我看了一场篮球赛,我想长大后我会比姚明还高,我将长到100米高。看完比赛后,我又回到学校上学。
下午放学后,我开始写作业。今天作业太多了,我不停的写啊,一直写到太阳从西边落下。
随机事件
不可能事件
必然事件
一休得罪了幕府将军,将军决定处罚一休,
幸得安国寺长老和百姓们的求情,将军终
于同意让一休用自己的聪明才智来决定自己的命运.
方法是将军写下两张签,一张罚,一张免,让一休抽签,抽中罚则罚,抽中免则免。
将军一心想处罚一休,将军会在写签时怎么写呢?
罚
免
请你用“随机事件;必然事件”等词语来分析两段内容.
爱动脑筋的一休早就料到了这一点。一休会用什么办
法应对狡诈的幕府将军呢?
一休
原来将军在两张签上都写上了“罚”。一休不论抽
到哪一张都一样要罚。
通过本节课的学习,请同学们谈谈你的体会与收获:
知识小结:
判断一事件属于哪一类事件
事先能否预料它会不会发生。
关键在于:
事先能预料一定发生:必然事件。
事先能预料一定不会发生:不可能事件。
事先不能预料会不会发生:随机事件
练习与质疑:
(1) 下列事件是随机事件的是( )
A: 人长生不老
B: 2012年奥运会中国队获100枚金牌
C: 掷两枚质地均匀的正方体骰子朝上一面的点数之积为21
D: 一个星期为七天
B
教材:P131-132 第1题
袋子里有红球、白球两种颜色的球从袋子里摸出一个球,有哪几种可能?
若红球、白球各有五个摸那种颜色的球可能性大?
若红球七个白球五个摸那种颜色的球可能性大?
课后思考
下课了!
生活是数学的源泉.
探索是数学的生命线.
结束寄语
生活是数学的源泉.
探索是数学的生命线.
概率论的产生和发展
概率论产生于十七世纪,本来是由保险事业的发展而产生的,但是来自于赌博者的请求,却是数学家们思考概率论问题的源泉。
传说早在1654年,有一个赌徒梅累向当时的数学家帕斯卡提出一个使他苦恼了很久的问题:“两个赌徒相约赌若干局,谁先赢 3局就算赢,全部赌本就归谁。但是当其中一个人赢了 2局,另一个人赢了1局的时候,由于某种原因,赌博终止了。问:赌本应该如何分法才合理?”
帕斯卡是17世纪著名的数学家,但这个问题却让他苦苦思索了三年,三年后,也就是1657年,荷兰著名的数学家惠更斯企图自己解决这一问题,结果写成了《论赌博中的计算》一书,这就是概率论最早的一部著作。
近几十年来,随着科技的蓬勃发展,概率论大量应用到国民经济、工农业生产及各学科领域。许多兴起的应用数学,如信息论、对策论、排队论、控制论等,都是以概率论作为基础的。
25.1 随机事件与概率
25.1.1 随机事件
小明从盒中任意摸出一球,一定能摸到红球吗?
不一定.
小麦和小米也能摸到红球吗?
一定摸不到红球。
一定摸到红球。
三人每次都能摸到红球吗?
可能发生也可能不发生。
必然发生
不可能发生
问题1:5名同学参加演讲比赛,以抽签方式决定每个人的出场顺序。签筒中有5根形状、大小完全相同的纸签,上面分别标有出场的序号1、2、3、4、5,小军首先抽签,他在看不到纸签上数字的情况下从筒中随机(任意)地取一根纸签,请考虑以下问题:
⑴抽到的序号有几种可能情况?
⑵抽到的序号小于6吗?
⑶抽到的序号会是0吗?
⑷抽到的序号是1吗?
每次抽签的结果有5种,每次不一定相同,可能是1、2、3、4、5中的任意一张.
只能是这5张中的一张,序号肯定是小于6的.
抽到序号不会是0,只会大于0.
抽到的序号可能是1,也可能不是1,但事先无法确定.
小伟掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,请考虑以下问题:掷一次骰子,在骰子向上的一面上,
(1)可能出现哪些点数?
(2)出现的点数大于0吗?
(3)出现在的点数会是7吗?
(4)出现的点数会是4吗?
问题2
可能是1、2、3、4、5、6中的任意一个点数.
出现的点数一定大于0.
抽到序号不可能是7.
抽到的序号可能是4,也可能不是4,但事先无法确定.
(1)生活中,有些事情我们事先能肯定它一定会发生,你能举出例子吗?
(2)生活中,有些事情我们事先能肯定它一定不会发生,你能举出例子吗?
(3)生活中,有些事情有时会发生,有时不会发生,你能举出例子吗?
试分析:“从一堆牌中任意抽一张抽到红牌”这一事件的发生情况
可能发生, 也可能不发生
必然发生
必然不会发生
必然会发生。
必然不会发生。
可能会发生,也可能不会发生。
1、在地球上,太阳每天从东方升起。
2、有一匹马奔跑的速度是70千米/秒。
3、明天,我买一注体育彩票,得500万大奖。
下列事件中哪些必然会发生,哪些必然不会发生,哪些可能会也可能不会发生?
6、2012年的中考,饶平县所城镇龙湾慈云中学15人考上饶平二中。
可能会发生,也可能不会发生。
5、掷一枚均匀的硬币,正面朝上。
可能会发生,也可能不会发生。
4、用长为3cm、4cm、7cm的三条线段首尾顺次连结,构成一个三角形。
必然不会发生。
在一定条件下:
必然会发生的事件称为必然事件;
必然不会发生的事件称为不可能事件;
可能会发生,也可能不发生的事件称为随机事件.
随机事件
随机事件
抛掷一枚硬币,正面向上。
木柴燃烧产生能量
明天地球还会转动
煮熟的鸭子,飞了。
太阳从西方升起
必然事件
必然事件
不可能事件
不可能事件
从一副牌中抽出黑桃K
3.篮球队员在罚球线上投篮一次,未投中。
4.度量三角形的内角和,结果是360°。
5.掷一次骰子,向上的一面是6点。
6.367人中至少有2个人的生日一样.
7.1+(-3)>-1。
巩固练习
必然事件
不可能事件
随机事件
随机事件
不可能事件
1.水温达到100摄氏度, 水就沸腾.
必然事件
2.汽车经过城市中某一有交通信号灯的路口,遇到红灯;
随机事件
8.某射击运动员射击一次,命中靶心。
随机事件
2011年11月28日 晴
早上,我迟到了。于是就急忙去学校上学,可是在楼梯上遇到了班主任,她批评了我一顿。我想我真不走运,她经常在办公室的啊,今天我真倒霉。我明天不能再迟到了,不然明天早上我将在楼梯上遇到班主任。
中午放学回家,我看了一场篮球赛,我想长大后我会比姚明还高,我将长到100米高。看完比赛后,我又回到学校上学。
下午放学后,我开始写作业。今天作业太多了,我不停的写啊,一直写到太阳从西边落下。
随机事件
不可能事件
必然事件
一休得罪了幕府将军,将军决定处罚一休,
幸得安国寺长老和百姓们的求情,将军终
于同意让一休用自己的聪明才智来决定自己的命运.
方法是将军写下两张签,一张罚,一张免,让一休抽签,抽中罚则罚,抽中免则免。
将军一心想处罚一休,将军会在写签时怎么写呢?
罚
免
请你用“随机事件;必然事件”等词语来分析两段内容.
爱动脑筋的一休早就料到了这一点。一休会用什么办
法应对狡诈的幕府将军呢?
一休
原来将军在两张签上都写上了“罚”。一休不论抽
到哪一张都一样要罚。
通过本节课的学习,请同学们谈谈你的体会与收获:
知识小结:
判断一事件属于哪一类事件
事先能否预料它会不会发生。
关键在于:
事先能预料一定发生:必然事件。
事先能预料一定不会发生:不可能事件。
事先不能预料会不会发生:随机事件
练习与质疑:
(1) 下列事件是随机事件的是( )
A: 人长生不老
B: 2012年奥运会中国队获100枚金牌
C: 掷两枚质地均匀的正方体骰子朝上一面的点数之积为21
D: 一个星期为七天
B
教材:P131-132 第1题
袋子里有红球、白球两种颜色的球从袋子里摸出一个球,有哪几种可能?
若红球、白球各有五个摸那种颜色的球可能性大?
若红球七个白球五个摸那种颜色的球可能性大?
课后思考
下课了!
生活是数学的源泉.
探索是数学的生命线.
结束寄语
同课章节目录
