_2020-2021学年九年级数学人教版下册第二十七章 相似 培优训练(Word版 含答案)
文档属性
| 名称 | _2020-2021学年九年级数学人教版下册第二十七章 相似 培优训练(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 806.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 11:42:02 | ||
图片预览


文档简介
人教版 九年级数学下册 第二十七章 相似 培优训练
一、选择题
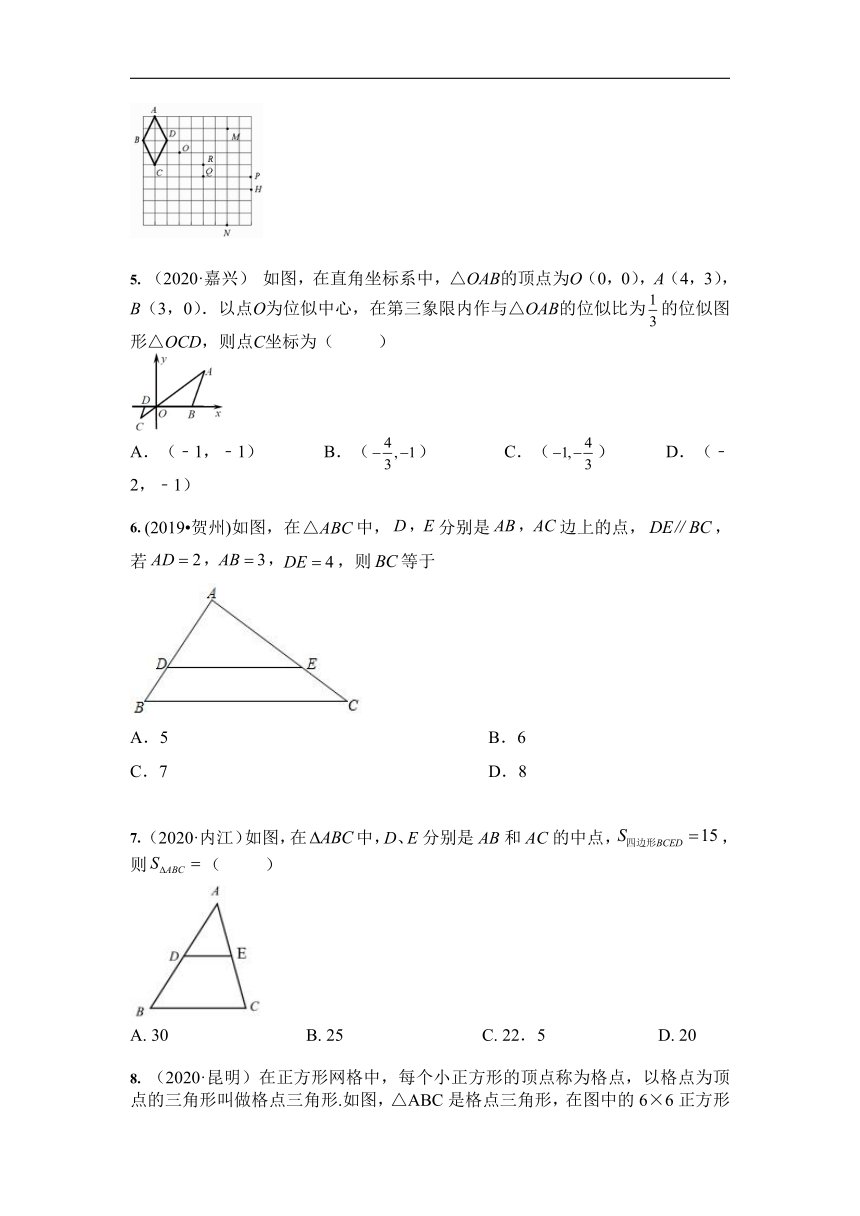
1. (2019?雅安)若,且,则的值是
A.4 B.2
C.20 D.14
2. (2019?雅安)如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与相似的是
A. B.
C. D.
3. (2020·重庆B卷)如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
4. (2020·河北) 在图5所示的网格中,以点O为位似中心,四边形ABCD的位似图形是
A.四边形NPMQ B.四边形NPMR
C.四边形NHMQ D.四边形NHMR
5. (2020·嘉兴) 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点C坐标为( )
A.(﹣1,﹣1) B.() C.() D.(﹣2,﹣1)
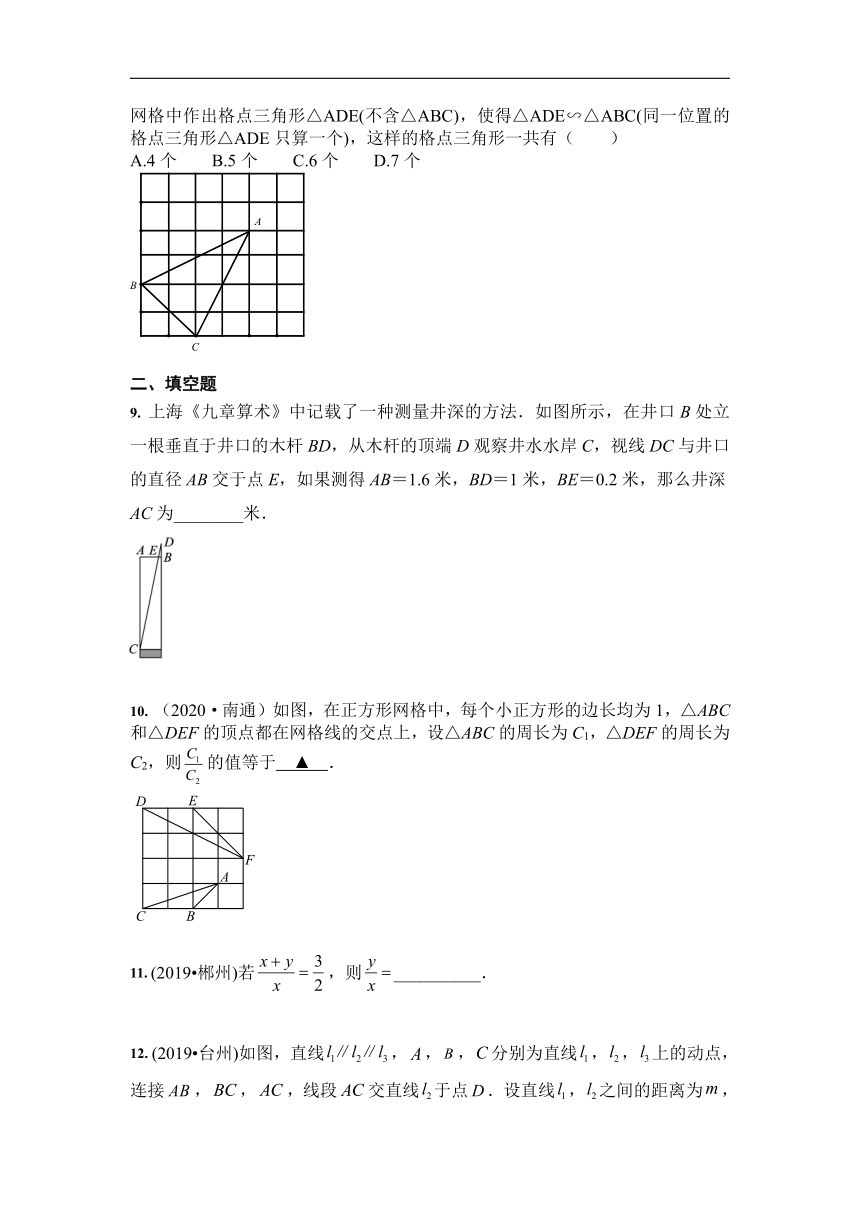
6. (2019?贺州)如图,在中,分别是边上的点,,若,则等于
A.5 B.6
C.7 D.8
7. (2020·内江)如图,在中,D、E分别是AB和AC的中点,,则( )
A. 30 B. 25 C. 22.5 D. 20
8. (2020·昆明)在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )
A.4个 B.5个 C.6个 D.7个
二、填空题
9. 上海《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.6米,BD=1米,BE=0.2米,那么井深AC为________米.
10. (2020·南通)如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上,设△ABC的周长为C1,△DEF的周长为C2,则的值等于 ▲ .
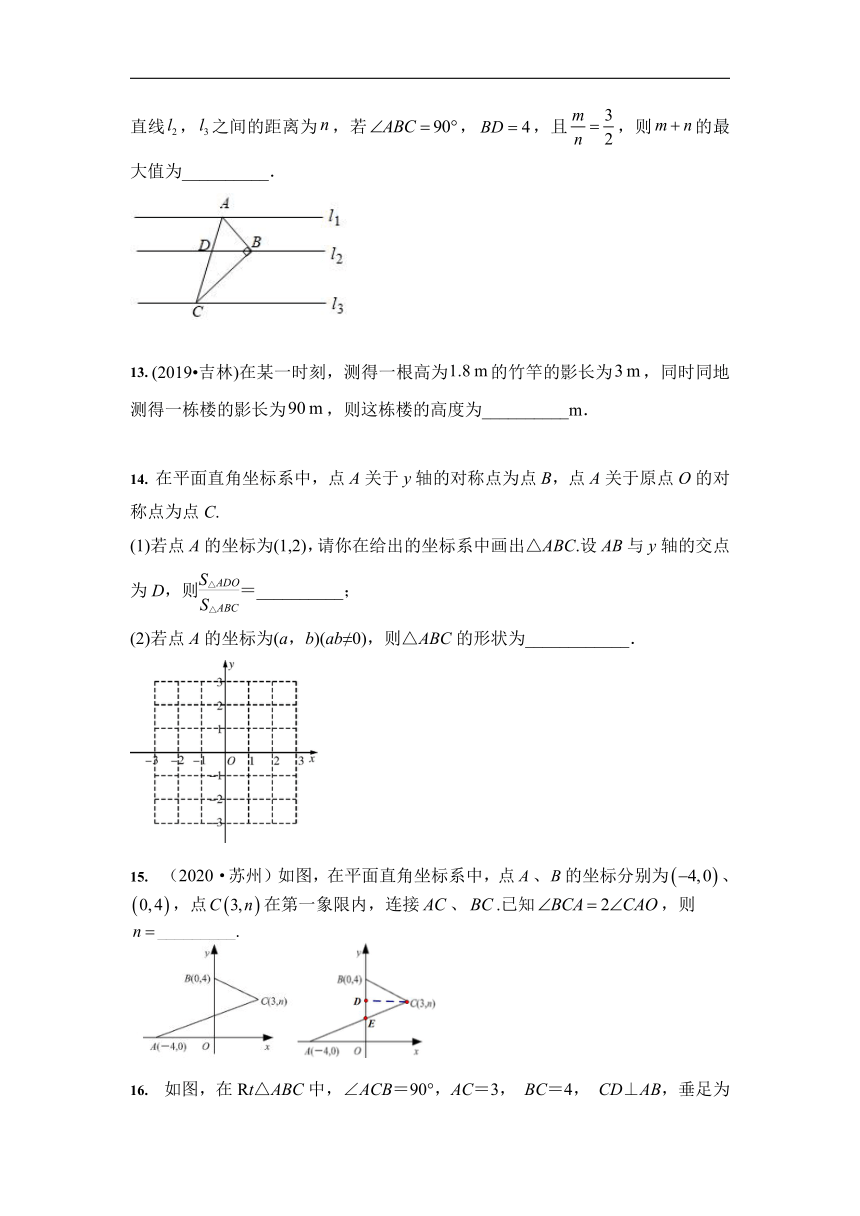
11. (2019?郴州)若,则__________.
12. (2019?台州)如图,直线,,,分别为直线,,上的动点,连接,,,线段交直线于点.设直线,之间的距离为,直线,之间的距离为,若,,且,则的最大值为__________.
13. (2019?吉林)在某一时刻,测得一根高为的竹竿的影长为,同时同地测得一栋楼的影长为,则这栋楼的高度为__________m.
14. 在平面直角坐标系中,点A关于y轴的对称点为点B,点A关于原点O的对称点为点C.
(1)若点A的坐标为(1,2),请你在给出的坐标系中画出△ABC.设AB与y轴的交点为D,则=__________;
(2)若点A的坐标为(a,b)(ab≠0),则△ABC的形状为____________.
15. (2020·苏州)如图,在平面直角坐标系中,点、的坐标分别为、,点在第一象限内,连接、.已知,则_________.
16. 如图,在Rt△ABC中,∠ACB=90°,AC=3, BC=4, CD⊥AB,垂足为D, E为BC的中点,AE与CD交于点F,则DF的长为_________.
三、解答题
17. 如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2:
(1)将△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
18. 如图,?ABCD的对角线AC,BD相交于点O,EF经过点O,与AB,CD分别交于点E,F,FE的延长线交CB的延长线于点M.
(1)求证:OE=OF;
(2)若AD=4,AB=6,BM=1,求BE的长.
19. (2020·苏州)如图,在矩形中,是的中点,,垂足为.
(1)求证:;
(2)若,,求的长.
20. 如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.
(1)写出图中两对相似三角形,并证明其中的一对;
(2)请连接FG,如果α=45°,AB=4,AF=3,求FG的长.
21. (2020·南京)如图,在△ABC和△A’B’C’中,D、D’分别是AB、A’B’上一点,=.
(1)当==时,求证:△ABC∽△A’B’C’.
证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当==时,判断△ABC与△A’B’C’是否相似,并说明理由.
22. (2019?菏泽)如图,和是有公共顶点的等腰直角三角形,.
(1)如图1,连接,,的廷长线交于点,交于点,求证:;
(2)如图2,把绕点顺时针旋转,当点落在上时,连接,,的延长线交于点,若,,求的面积.
23. 如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于点M,连接CM交DB于点N.
(1)求证:BD2=AD·CD;
(2)若CD=6,AD=8,求MN的长.
24. 如图,已知△ABC∽△A1B1C1,相似比为k(k>1),且△ABC的三边长分别为a、b、c(a>b>c),△A1B1C1的三边长分别为a1、b1、c1.
(1)若c=a1,求证:a=kc;
(2)若c=a1,试给出符合条件的一对△ABC和△A1B1C1,使得a、b、c和a1、b1、c1都是正整数,并加以说明;
(3)若b=a1,c=b1,是否存在△ABC和△A1B1C1使得k=2?请说明理由.
人教版 九年级数学下册 第二十七章 相似 培优训练-答案
一、选择题
1. 【答案】A
【解析】由a∶b=3∶4知,所以.
所以由得到:,
解得.所以.
所以.故选A.
2. 【答案】B
【解析】因为中有一个角是135°,选项中,有135°角的三角形只有B,且满足两边成比例夹角相等,故选B.
3. 【答案】C
【解析】本题考查了相似三角形的性质, ∵△ABC与△DEF位似,且,∴,因此本题选C.
4. 【答案】A
【解析】解析:连接AO并延长AO至点N,连接BO并延长PO至点P, 连接CO并延长CO至点M, 连接DO并延长DO至Q,可知,所以以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,故答案为A.
5. 【答案】B
【解析】本题考查了在坐标系中,位似图形点的坐标.在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(–kx,–ky).由A(4,3),位似比k=,可得C()因此本题选B.
6. 【答案】B
【解析】∵,∴,
∴,即,解得:,故选B.
7. 【答案】 D
【解析】本题考查了相似三角形的判定与性质,解答本题的关键是得出DE是中位线,从而判断△ADE∽△ABC,然后掌握相似三角形的面积比等于相似比的平方即可求解本题.首先判断出△ADE∽△ABC,然后根据相似三角形的面积比等于相似比的平方即可求出△ABC的面积.
根据题意,点D和点E分别是AB和AC的中点,则DE∥BC且DE=BC,故可以判断出△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方,可知:=1:4,则:=3:4,题中已知,故可得=5,=20,因此本题选D.
8. 【答案】A
【解析】本题考查了相似三角形的判定.符合条件的三角形有四个,如图所示:
因此本题选A.
二、填空题
9. 【答案】7 [解析] ∵BD⊥AB,AC⊥AB,
∴BD∥AC,∴△ACE∽△BDE,
∴=,∴=,∴AC=7.
10. 【答案】
【解析】由图形易证△ABC与△DEF相似,且相似比为,所以周长比为.故答案为:.
11. 【答案】
【解析】∵,∴,
故2y=x,则,故答案为:.
12. 【答案】
【解析】如图,过作于,延长交于,过作于,过作于,
设,,,,
∵,∴,,
∵,
∴,
∴,∴,
∴,即,∴,
∵,∴,
∴,即,
∴,
∵,∴,
∴,
∴当最大时,,
∵,
∴当时,,
∴,
∴的最大值为.故答案为:.
13. 【答案】54
【解析】设这栋楼的高度为h m,
∵在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时测得一栋楼的影长为60 m,
∴,解得h=54(m).故答案为:54.
14. 【答案】(1)△ABC如图 (2)直角三角形 解析:(1)因为点A的坐标为(1,2),所以点A关于y轴的对称点B的坐标为(-1,2),关于原点的对称点C的坐标为(-1,-2).连AB,BC,AC,作△ABC.
设AB交y轴于D点,如图,
D点坐标为(0,2),
∵OD∥BC,
∴△ADO∽△ABC.
∴==.
(2)∵ab≠0,∴a≠0,且b≠0,
∴点A不在坐标轴上,
∴AB∥x轴,BC⊥x轴.
∴∠ABC=90°.
∴△ABC是直角三角形.
15. 【答案】或2.8
【解析】本题考查了平面直角坐标系中点的坐标特征,等腰三角形的性质,相似三角形的判定和性质,过点C作CD⊥y轴于点D,设AC交y轴于点E,∴CD∥x轴,∴∠CAO=∠ACD, △DEC∽△OEA,∵,∴∠BCD=∠ACD, ∴BD=DE,设BD=DE=x,则OE=4-2x,∴=,即=,解得x=1.2.∴OE=4-2x=1.6,∴n=OD=DE+OE=1.2+1.6=2.8.
16. 【答案】
【解析】本题考查平行线分线段成比例定理,相似三角形的判定与性质.已知∠ACB=90°,AC=3, BC=4,由勾股定理,得AB=5.CD⊥AB,由三角形的面积,得CD==.易得△ABC∽△ACD∽△CBD,由相似三角形对应边成比例,得AD==,BD==.过点E作EG∥AB交CD于点G,由平行线分线段成比例,得DG=CD=,EG=,所以,即,所以DF=,故答案为.
三、解答题
17. 【答案】
解:(1)正确图形如解图.
(2)正确图形如解图.
解图
18. 【答案】
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,OB=OD,∴∠ABO=∠CDO.
又∵∠BOE=∠DOF,∴△BOE≌△DOF,
∴OE=OF.
(2)由平行四边形的性质可知DC=AB=6,BC=AD=4,
∴CM=BM+BC=5.
由(1)可知△BOE≌△DOF,
∴DF=BE,
∴CF=CD-DF=6-BE.
∵AB∥CD,∴△MBE∽△MCF,
∴=,即=,∴BE=1.
19. 【答案】
解: 证明:(1)∵四边形是矩形,∴,.∴,
∵,∴.∴,∴.
解:(2)∵,∴.
∵,是的中点,∴.∴在中,.
又∵,∴,∴.
20. 【答案】
解:(1)△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM等.(写出两对即可)
以下证明△AMF∽△BGM.
由题知∠A=∠B=∠DME=α,而∠AFM=∠DME+∠E,
∠BMG=∠A+∠E,∴∠AFM=∠BMG,∴△AMF∽△BGM.
(2)当α=45°时,可得AC⊥BC且AC=BC,∵M为AB中点,
∴AM=BM=2.
由△AMF∽△BGM得,AF·BG=AM·BM,∴BG=.
又AC=BC=4cos45°=4,∴CG=4-=,CF=4-3=1,∴FG==.
21. 【答案】
解:(1) == ∠A=∠A’.
(2)如图,过点D、D’分别作DE∥BC,D’E’∥B’C’,DE交AC于点E,D’E’交A’C’于点E’.
∵DE∥BC,
∴△ADE∽△ABC.
∴==.
同理==.
又=,
∴=,
∴=.
同理 =.
∴=,即=.
∴=.
又==,
∴==,
∴△DCE∽△D’C’E’.
∴∠CED=∠C’E’D’.
∵DE∥BC,
∴∠CED+∠ACB=180°.
同理 ∠C’E’D’+∠A’C’B’=180°.
∴∠ACB=∠A’C’B’.
又=
∴△ABC∽△A’B’C’.
22. 【答案】
(1)∵和是有公共顶点的等腰直角三角形,,
∴,,,
即,
在与中,,
∴,∴,
∵,
∴,∴.
(2)在与中,,
∴,
∴,,
∵,
∴,
∴,
∵,,
∴,,
∴,,
∵,
∴,
∴,
∴,,
∴,
∴的面积.
23. 【答案】
解:(1)证明:∵DB平分∠ADC,
∴∠ADB=∠BDC.
又∵∠ABD=∠BCD=90°,
∴△ABD∽△BCD,
∴=,即BD2=AD·CD.
(2)∵BM∥CD,
∴BM⊥BC,∠MBD=∠CDB=∠MDB,
∴MB=MD.
∵∠A+∠MDB=90°,∠MBA+∠MBD=90°,
∴∠A=∠MBA,∴MB=MA,
∴MB=MA=MD=AD=4.
由(1)可知BD2=AD·CD=48.
∴BC==2 ,
∴MC==2 .
∵BM∥CD,∴△MNB∽△CND,
∴=,即=,
∴MN= .
24. 【答案】
(1)证明:∵△ABC∽△A1B1C1,且相似比为k(k>1),
∴=k.∴a=ka1,又∵c=a1,∴a=kc.
(2)解:取a=8,b=6,c=4,同时取a1=4,b1=3,c1=2.
此时===2,∴△ABC∽△A1B1C1且c=a1.
(3)解:不存在这样的△ABC和△A1B1C1.理由如下:
若k=2,则a=2a1,b=2b1,c=2c1.
又∵b=a1,c=b1,
∴a=2a1=2b=4b1=4c,
∴b=2c.(12分)
∴b+c=2c+c<4c=a,与b+c>a矛盾,
故不存在这样的△ABC和△A1B1C1,使得k=2.
一、选择题
1. (2019?雅安)若,且,则的值是
A.4 B.2
C.20 D.14
2. (2019?雅安)如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与相似的是
A. B.
C. D.
3. (2020·重庆B卷)如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:5
4. (2020·河北) 在图5所示的网格中,以点O为位似中心,四边形ABCD的位似图形是
A.四边形NPMQ B.四边形NPMR
C.四边形NHMQ D.四边形NHMR
5. (2020·嘉兴) 如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作与△OAB的位似比为的位似图形△OCD,则点C坐标为( )
A.(﹣1,﹣1) B.() C.() D.(﹣2,﹣1)
6. (2019?贺州)如图,在中,分别是边上的点,,若,则等于
A.5 B.6
C.7 D.8
7. (2020·内江)如图,在中,D、E分别是AB和AC的中点,,则( )
A. 30 B. 25 C. 22.5 D. 20
8. (2020·昆明)在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )
A.4个 B.5个 C.6个 D.7个
二、填空题
9. 上海《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D观察井水水岸C,视线DC与井口的直径AB交于点E,如果测得AB=1.6米,BD=1米,BE=0.2米,那么井深AC为________米.
10. (2020·南通)如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上,设△ABC的周长为C1,△DEF的周长为C2,则的值等于 ▲ .
11. (2019?郴州)若,则__________.
12. (2019?台州)如图,直线,,,分别为直线,,上的动点,连接,,,线段交直线于点.设直线,之间的距离为,直线,之间的距离为,若,,且,则的最大值为__________.
13. (2019?吉林)在某一时刻,测得一根高为的竹竿的影长为,同时同地测得一栋楼的影长为,则这栋楼的高度为__________m.
14. 在平面直角坐标系中,点A关于y轴的对称点为点B,点A关于原点O的对称点为点C.
(1)若点A的坐标为(1,2),请你在给出的坐标系中画出△ABC.设AB与y轴的交点为D,则=__________;
(2)若点A的坐标为(a,b)(ab≠0),则△ABC的形状为____________.
15. (2020·苏州)如图,在平面直角坐标系中,点、的坐标分别为、,点在第一象限内,连接、.已知,则_________.
16. 如图,在Rt△ABC中,∠ACB=90°,AC=3, BC=4, CD⊥AB,垂足为D, E为BC的中点,AE与CD交于点F,则DF的长为_________.
三、解答题
17. 如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2:
(1)将△ABC先向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
18. 如图,?ABCD的对角线AC,BD相交于点O,EF经过点O,与AB,CD分别交于点E,F,FE的延长线交CB的延长线于点M.
(1)求证:OE=OF;
(2)若AD=4,AB=6,BM=1,求BE的长.
19. (2020·苏州)如图,在矩形中,是的中点,,垂足为.
(1)求证:;
(2)若,,求的长.
20. 如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.
(1)写出图中两对相似三角形,并证明其中的一对;
(2)请连接FG,如果α=45°,AB=4,AF=3,求FG的长.
21. (2020·南京)如图,在△ABC和△A’B’C’中,D、D’分别是AB、A’B’上一点,=.
(1)当==时,求证:△ABC∽△A’B’C’.
证明的途径可以用下面的框图表示,请填写其中的空格.
(2)当==时,判断△ABC与△A’B’C’是否相似,并说明理由.
22. (2019?菏泽)如图,和是有公共顶点的等腰直角三角形,.
(1)如图1,连接,,的廷长线交于点,交于点,求证:;
(2)如图2,把绕点顺时针旋转,当点落在上时,连接,,的延长线交于点,若,,求的面积.
23. 如图,∠ABD=∠BCD=90°,DB平分∠ADC,过点B作BM∥CD交AD于点M,连接CM交DB于点N.
(1)求证:BD2=AD·CD;
(2)若CD=6,AD=8,求MN的长.
24. 如图,已知△ABC∽△A1B1C1,相似比为k(k>1),且△ABC的三边长分别为a、b、c(a>b>c),△A1B1C1的三边长分别为a1、b1、c1.
(1)若c=a1,求证:a=kc;
(2)若c=a1,试给出符合条件的一对△ABC和△A1B1C1,使得a、b、c和a1、b1、c1都是正整数,并加以说明;
(3)若b=a1,c=b1,是否存在△ABC和△A1B1C1使得k=2?请说明理由.
人教版 九年级数学下册 第二十七章 相似 培优训练-答案
一、选择题
1. 【答案】A
【解析】由a∶b=3∶4知,所以.
所以由得到:,
解得.所以.
所以.故选A.
2. 【答案】B
【解析】因为中有一个角是135°,选项中,有135°角的三角形只有B,且满足两边成比例夹角相等,故选B.
3. 【答案】C
【解析】本题考查了相似三角形的性质, ∵△ABC与△DEF位似,且,∴,因此本题选C.
4. 【答案】A
【解析】解析:连接AO并延长AO至点N,连接BO并延长PO至点P, 连接CO并延长CO至点M, 连接DO并延长DO至Q,可知,所以以点O为位似中心,四边形ABCD的位似图形是四边形NPMQ,故答案为A.
5. 【答案】B
【解析】本题考查了在坐标系中,位似图形点的坐标.在平面直角坐标系中,如果以原点为位似中心,画出一个与原图形位似的图形,使它与原图形的相似比为k,那么与原图形上的点(x,y)对应的位似图形上的点的坐标为(kx,ky)或(–kx,–ky).由A(4,3),位似比k=,可得C()因此本题选B.
6. 【答案】B
【解析】∵,∴,
∴,即,解得:,故选B.
7. 【答案】 D
【解析】本题考查了相似三角形的判定与性质,解答本题的关键是得出DE是中位线,从而判断△ADE∽△ABC,然后掌握相似三角形的面积比等于相似比的平方即可求解本题.首先判断出△ADE∽△ABC,然后根据相似三角形的面积比等于相似比的平方即可求出△ABC的面积.
根据题意,点D和点E分别是AB和AC的中点,则DE∥BC且DE=BC,故可以判断出△ADE∽△ABC,根据相似三角形的面积比等于相似比的平方,可知:=1:4,则:=3:4,题中已知,故可得=5,=20,因此本题选D.
8. 【答案】A
【解析】本题考查了相似三角形的判定.符合条件的三角形有四个,如图所示:
因此本题选A.
二、填空题
9. 【答案】7 [解析] ∵BD⊥AB,AC⊥AB,
∴BD∥AC,∴△ACE∽△BDE,
∴=,∴=,∴AC=7.
10. 【答案】
【解析】由图形易证△ABC与△DEF相似,且相似比为,所以周长比为.故答案为:.
11. 【答案】
【解析】∵,∴,
故2y=x,则,故答案为:.
12. 【答案】
【解析】如图,过作于,延长交于,过作于,过作于,
设,,,,
∵,∴,,
∵,
∴,
∴,∴,
∴,即,∴,
∵,∴,
∴,即,
∴,
∵,∴,
∴,
∴当最大时,,
∵,
∴当时,,
∴,
∴的最大值为.故答案为:.
13. 【答案】54
【解析】设这栋楼的高度为h m,
∵在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时测得一栋楼的影长为60 m,
∴,解得h=54(m).故答案为:54.
14. 【答案】(1)△ABC如图 (2)直角三角形 解析:(1)因为点A的坐标为(1,2),所以点A关于y轴的对称点B的坐标为(-1,2),关于原点的对称点C的坐标为(-1,-2).连AB,BC,AC,作△ABC.
设AB交y轴于D点,如图,
D点坐标为(0,2),
∵OD∥BC,
∴△ADO∽△ABC.
∴==.
(2)∵ab≠0,∴a≠0,且b≠0,
∴点A不在坐标轴上,
∴AB∥x轴,BC⊥x轴.
∴∠ABC=90°.
∴△ABC是直角三角形.
15. 【答案】或2.8
【解析】本题考查了平面直角坐标系中点的坐标特征,等腰三角形的性质,相似三角形的判定和性质,过点C作CD⊥y轴于点D,设AC交y轴于点E,∴CD∥x轴,∴∠CAO=∠ACD, △DEC∽△OEA,∵,∴∠BCD=∠ACD, ∴BD=DE,设BD=DE=x,则OE=4-2x,∴=,即=,解得x=1.2.∴OE=4-2x=1.6,∴n=OD=DE+OE=1.2+1.6=2.8.
16. 【答案】
【解析】本题考查平行线分线段成比例定理,相似三角形的判定与性质.已知∠ACB=90°,AC=3, BC=4,由勾股定理,得AB=5.CD⊥AB,由三角形的面积,得CD==.易得△ABC∽△ACD∽△CBD,由相似三角形对应边成比例,得AD==,BD==.过点E作EG∥AB交CD于点G,由平行线分线段成比例,得DG=CD=,EG=,所以,即,所以DF=,故答案为.
三、解答题
17. 【答案】
解:(1)正确图形如解图.
(2)正确图形如解图.
解图
18. 【答案】
解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,OB=OD,∴∠ABO=∠CDO.
又∵∠BOE=∠DOF,∴△BOE≌△DOF,
∴OE=OF.
(2)由平行四边形的性质可知DC=AB=6,BC=AD=4,
∴CM=BM+BC=5.
由(1)可知△BOE≌△DOF,
∴DF=BE,
∴CF=CD-DF=6-BE.
∵AB∥CD,∴△MBE∽△MCF,
∴=,即=,∴BE=1.
19. 【答案】
解: 证明:(1)∵四边形是矩形,∴,.∴,
∵,∴.∴,∴.
解:(2)∵,∴.
∵,是的中点,∴.∴在中,.
又∵,∴,∴.
20. 【答案】
解:(1)△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM等.(写出两对即可)
以下证明△AMF∽△BGM.
由题知∠A=∠B=∠DME=α,而∠AFM=∠DME+∠E,
∠BMG=∠A+∠E,∴∠AFM=∠BMG,∴△AMF∽△BGM.
(2)当α=45°时,可得AC⊥BC且AC=BC,∵M为AB中点,
∴AM=BM=2.
由△AMF∽△BGM得,AF·BG=AM·BM,∴BG=.
又AC=BC=4cos45°=4,∴CG=4-=,CF=4-3=1,∴FG==.
21. 【答案】
解:(1) == ∠A=∠A’.
(2)如图,过点D、D’分别作DE∥BC,D’E’∥B’C’,DE交AC于点E,D’E’交A’C’于点E’.
∵DE∥BC,
∴△ADE∽△ABC.
∴==.
同理==.
又=,
∴=,
∴=.
同理 =.
∴=,即=.
∴=.
又==,
∴==,
∴△DCE∽△D’C’E’.
∴∠CED=∠C’E’D’.
∵DE∥BC,
∴∠CED+∠ACB=180°.
同理 ∠C’E’D’+∠A’C’B’=180°.
∴∠ACB=∠A’C’B’.
又=
∴△ABC∽△A’B’C’.
22. 【答案】
(1)∵和是有公共顶点的等腰直角三角形,,
∴,,,
即,
在与中,,
∴,∴,
∵,
∴,∴.
(2)在与中,,
∴,
∴,,
∵,
∴,
∴,
∵,,
∴,,
∴,,
∵,
∴,
∴,
∴,,
∴,
∴的面积.
23. 【答案】
解:(1)证明:∵DB平分∠ADC,
∴∠ADB=∠BDC.
又∵∠ABD=∠BCD=90°,
∴△ABD∽△BCD,
∴=,即BD2=AD·CD.
(2)∵BM∥CD,
∴BM⊥BC,∠MBD=∠CDB=∠MDB,
∴MB=MD.
∵∠A+∠MDB=90°,∠MBA+∠MBD=90°,
∴∠A=∠MBA,∴MB=MA,
∴MB=MA=MD=AD=4.
由(1)可知BD2=AD·CD=48.
∴BC==2 ,
∴MC==2 .
∵BM∥CD,∴△MNB∽△CND,
∴=,即=,
∴MN= .
24. 【答案】
(1)证明:∵△ABC∽△A1B1C1,且相似比为k(k>1),
∴=k.∴a=ka1,又∵c=a1,∴a=kc.
(2)解:取a=8,b=6,c=4,同时取a1=4,b1=3,c1=2.
此时===2,∴△ABC∽△A1B1C1且c=a1.
(3)解:不存在这样的△ABC和△A1B1C1.理由如下:
若k=2,则a=2a1,b=2b1,c=2c1.
又∵b=a1,c=b1,
∴a=2a1=2b=4b1=4c,
∴b=2c.(12分)
∴b+c=2c+c<4c=a,与b+c>a矛盾,
故不存在这样的△ABC和△A1B1C1,使得k=2.
