2.5.2矩形的判定 同步练习(含解析)
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册2.5.2矩形的判定
同步练习
一、单选题
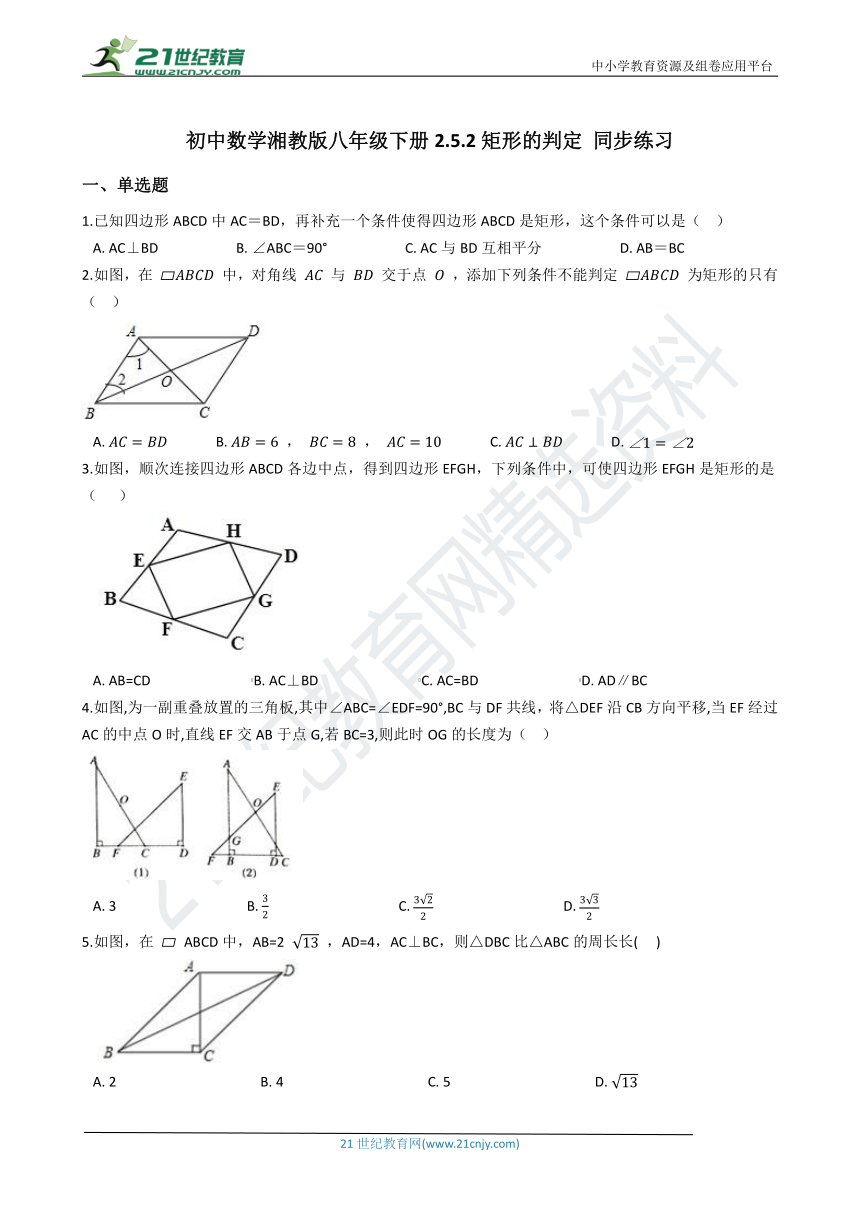
1.已知四边形ABCD中AC=BD,再补充一个条件使得四边形ABCD是矩形,这个条件可以是(??
)
A.?AC⊥BD??????????????????????B.?∠ABC=90°??????????????????????C.?AC与BD互相平分??????????????????????D.?AB=BC
2.如图,在
中,对角线
与
交于点
,添加下列条件不能判定
为矩形的只有(??
)
A.???????????????B.?
,
,
??????????????C.???????????????D.?
3.如图,顺次连接四边形ABCD各边中点,得到四边形EFGH,下列条件中,可使四边形EFGH是矩形的是(????
)
A.?AB=CD?????????????????????????????B.?AC⊥BD?????????????????????????????C.?AC=BD?????????????????????????????D.?AD∥BC
4.如图,为一副重叠放置的三角板,其中∠ABC=∠EDF=90°,BC与DF共线,将△DEF沿CB方向平移,当EF经过AC的中点O时,直线EF交AB于点G,若BC=3,则此时OG的长度为(??
)
A.?3??????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
5.如图,在
ABCD中,AB=2
,AD=4,AC⊥BC,则△DBC比△ABC的周长长(???
)
A.?2??????????????????????????????????????????B.?4??????????????????????????????????????????C.?5??????????????????????????????????????????D.?
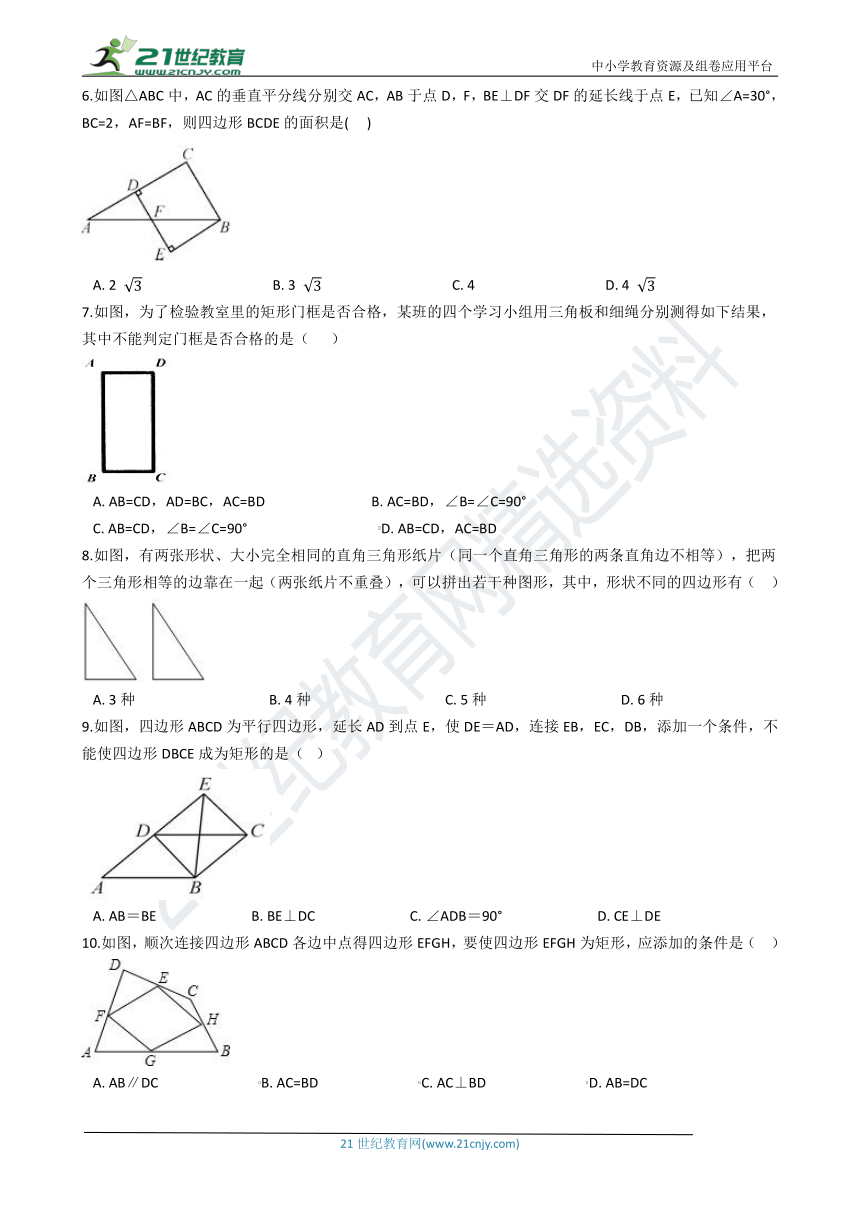
6.如图△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是(???
)
A.?2
??????????????????????????????????????B.?3
??????????????????????????????????????C.?4??????????????????????????????????????D.?4
7.如图,为了检验教室里的矩形门框是否合格,某班的四个学习小组用三角板和细绳分别测得如下结果,其中不能判定门框是否合格的是(????
)
A.?AB=CD,AD=BC,AC=BD???????????????????????????????B.?AC=BD,∠B=∠C=90°
C.?AB=CD,∠B=∠C=90°??????????????????????????????????????D.?AB=CD,AC=BD
8.如图,有两张形状、大小完全相同的直角三角形纸片(同一个直角三角形的两条直角边不相等),把两个三角形相等的边靠在一起(两张纸片不重叠),可以拼出若干种图形,其中,形状不同的四边形有(??
)
A.?3种???????????????????????????????????????B.?4种???????????????????????????????????????C.?5种???????????????????????????????????????D.?6种
9.如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是(?
)
A.?AB=BE???????????????????????????B.?BE⊥DC???????????????????????????C.?∠ADB=90°???????????????????????????D.?CE⊥DE
10.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是(??
)
A.?AB∥DC?????????????????????????????B.?AC=BD?????????????????????????????C.?AC⊥BD?????????????????????????????D.?AB=DC
二、填空题
11.如图,为了检查平行四边形书架
ABCD
的侧边是否与上、下边都垂直,工人师傅用一根绳子比较了其对角线
AC,BD
的长度,若二者长度相等,则该书架的侧边与上、下边都垂直,请你说出其中的数学原理________.
12.如图,平行四边形ABCD中,∠DAB=70°,将平行四边形ABCD变化为一个矩形(图中的虚线部分),在此过程中,分析每条边的运动.AB:________;AD:________;BC:________;CD:________.
13.如图,点E、F、G、H分别是矩形ABCD边AB、BC、CD、DA上的点,且HG与EF交于点I,连接HE、FG,若AB=6,BC=5,EF//AD,HG//AB,则HE+FG的最小值是________
.
14.如图,在矩形ABCD中,BC=40cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和1cm/s,则最快________s后,四边ABPQ成为矩形.
三、解答题
15.如图,在△ABC中,AB=AC,D为BC边的中点,以AB、BD为邻边作?ABDE,连接AD,EC.求证:四边形ADCE是矩形.
16.如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形,求证:四边形ADCE是矩形.
17.如图,
的对角线AC,
BD相交于点O,将△ABO平移到△DCE,已知AO=
1,
BO=2,
,求证:四边形OCED是矩形.
四、综合题
18.
ABCD中,过点D作DE⊥AB于点E,点F在CD上,DF=BE,连接:BF,AF。
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE-3,DF=5,求矩形BFDE的面积。
答案解析部分
一、单选题
1.【答案】
C
【解析】【解答】解:四边形ABCD中AC=BD,再补充一个条件使得四边形ABCD是矩形,这个条件可以是AC与BD互相平分,理由如下:
∵在四边形ABCD中,对角线AC,BD互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴四边形ABCD是矩形.
故答案为:C.
【分析】四边形ABCD中,对角线AC,BD互相平分,得四边形ABCD是平行四边形,又由AC=BD,即可求得答案.
2.【答案】
C
【解析】【解答】解:A.
,对角线相等,可以判定
为矩形
,此选项不符合题意
;
B.
,
,
,可知△ABC为直角三角形,且∠ABC=90°,故可以判定
为矩形,此选项不符合题意
;
C.
,可以判定
为菱形,此选项符合题意
;
?
D.
,可得AO=BO,故AC=BD,可以判定
为矩形,此选项不符合题意
.
故答案为:C.
【分析】根据矩形的判定“有一个角是直角的平行四边形是矩形;对角线相等的平行四边形是矩形”即可判断求解.
3.【答案】
B
【解析】【解答】解:连接AC,BD,
∵顺次连接四边形ABCD各边中点,得到四边形EFGH,
∴EF∥HG∥AC,EH∥FG∥BD,
要使四边形EFGH为矩形,
则EF⊥EH,
故EF⊥AC,
则AC⊥BD,
故答案为:B
【分析】连接AC,BD,根据中位线的性质及矩形的判定方法即可求解.
4.【答案】
C
【解析】【解答】解:过O作OH⊥BC于H,过G作GI⊥OH于I
,
∵∠ABC=90°,
∴AB⊥BC,
∴OH∥AB,
又O为中点,
∴H为BC的中点,
∴BH=
BC=
,
∵GI⊥OH,
∴四边形BHIG为矩形,
∴GI∥BH,GI=BH=
,
又∠F=45°,
∴∠OGI=45°,
∴OG=
.
【分析】过O作OH⊥BC于H,过G作GI⊥OH于I
,根据同一平面内垂直于同一直线的两条直线互相平行得出OH∥AB,根据三角形中位线的判定定理的逆用得出H为BC的中点,故BH=
BC=
,很容易判断出四边形BHIG为矩形,根据矩形的性质得出GI∥BH,GI=BH=
,从而根据等腰直角三角形的性质得出OG的长。
5.【答案】
B
【解析】【解答】解:过点D作DG⊥BC,交BC的延长线于点G,
∵平行四边形ABCD,
∴AD=BC=4,AB=CD=
,
AD∥BC?????
∵AC⊥BC
∴AC⊥AD
∴∠CAD=∠ACG=∠DGC=90°
∴四边形ACGD是矩形,
∴AD=CG;
∴BG=BC+CG=4+4=8;
在Rt△ABC中,
在Rt△BDC中,
∴
△DBC和△ABC的周长差为
BD+BC+DC-AB-AC-BC=BD-AC=10-6=4.
故答案为:4.
【分析】过点D作DG⊥BC,交BC的延长线于点G,利用平行四边形的性质,可证得AD=BC=4,AB=CD=
,
AD∥BC,再证明四边形ACGD是矩形,根据矩形的性质,可证得AD=CG,由此可求出BG的长,然后利用勾股定理求出BD,AC的长,再求出△DBC和△ABC的周长差就是BD与AC的差,即可求出结果。
6.【答案】
A
【解析】【解答】解:∵DE是AC的垂直的平分线,F是AB的中点,
∴DF∥BC,
∴∠C=90°,
∴四边形BCDE是矩形.
∵∠A=30°,∠C=90°,BC=2,
∴AB=4,
∴AC=
=2
.
∴BE=CD=
.
∴四边形BCDE的面积为:2×
=2
.
故答案为:A.
【分析】根据三角形的中位线定理得到DF∥BC,由∠C=90°,得到四边形BCDE是矩形;根据勾股定理求出BE=CD的值,求出四边形BCDE的面积.
7.【答案】
D
【解析】【解答】A、∵AB=CD,AD=BC,∴四边形ABCD是平行四边形,
∵AC=BD,∴四边形ABCD是矩形,
故能判定门框合格;
B、在Rt△ABC和Rt△DCB中,
,
∴Rt△ABC≌Rt△DCB(HL),
∴AB=CD,
∵∠B=∠C=90°,∴AB∥CD,
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
故能判定门框合格;
C、∵∠B=∠C=90°,∴AB∥CD,
∵AB=CD,
∴四边形ABCD是平行四边形,
∵∠B=∠C=90°,
∴四边形ABCD是矩形,
故能判定门框合格;
D、当四边形ABCD是等腰梯形时,也满足AB=CD,AC=BD,故不能判定门框合格.
故答案为:D.
【分析】条件中只给出了三角板和绳子,所以可以测量四条边的长,如果对边分别相等,可以判定为平行四边形,再测量对角线,如果对角线也相等则为矩形.
8.【答案】
B
【解析】【解答】如图,①②③,
;
;
共有4种情况,两种平行四边形,矩形和一般的四边形;
故答案为:B.
【分析】根据题意将所有情况列出即可.
9.【答案】
B
【解析】【解答】解:A、∵四边形ABCD为平行四边形,∴BC∥AD,AD=BC,
∴DE=BC,
∴四边形DBCE是平行四边形(一组对边平行且相等的四边形是平行四边形),
∵AB=BE,∴△ABE是等腰三角形,
∵DE=AD,∴BD⊥DE,
∴四边形DBCE是矩形,正确,不符合题意;
B、由A知四边形DBCE是平行四边形,?
BE⊥DC?,∴四边形DBCE是菱形,错误,不符合题意.
C、由A知四边形DBCE是平行四边形,?∵∠ADB=90°
,∴四边形DBCE是矩形,正确,不符合题意;
D、由A知四边形DBCE是平行四边形,?∵CE⊥DE,∠DEC=90°
,∴四边形DBCE是矩形,正确,不符合题意;
故答案为:B.
【分析】由平行四边形的性质,结合DE=AD,可证四边形DBCE是平行四边形,由于AB=CE,利用等腰三角形的性质可得BD⊥DE,则由一个角是直角的平行四边形是矩形可证四边形DBCE是矩形;CD都可依据一个角是直角的平行四边形是矩形可证四边形DBCE是矩形;而B项对角线互相垂直只能得出四边形DBCE是菱形.
10.【答案】
C
【解析】【解答】解:依题意得,四边形EFGH是由四边形ABCD各边中点连接而成,
连接AC、BD,
故EF∥AC∥HG,EH∥BD∥FG,
所以四边形EFGH是平行四边形,
要使四边形EFGH为矩形,
根据矩形的判定(有一个角为直角的平行四边形是矩形)
故当AC⊥BD时,∠EFG=∠EHG=90度.四边形EFGH为矩形.
故选C.
【分析】根据矩形的判定定理(有一个角为直角的平行四边形是矩形).先证四边形EFGH是平行四边形,要使四边形EFGH为矩形,需要∠EFG=90度.由此推出AC⊥BD.
二、填空题
11.【答案】
对角线相等的平行四边形是矩形,矩形的四个角都是直角;
【解析】【解答】因为平行四边形ABCD的对角线相等,所以四边形ABCD是矩形,而矩形的四个角都是直角.
故答案是:对角线相等的平行四边形是矩形,矩形的四个角都是直角
【分析】根据矩形的判定和性质定理,即可解答.
12.【答案】
不动;绕点A沿逆时针旋转20°;绕点B沿逆时针旋转20°;平移
【解析】【解答】ABCD是平行四边形,两组对边分别平行,只要保证一个角为90°,则四边形ABCD即为矩形.
【分析】熟练掌握矩形的判定.平行四边形只要保证一个角为直角,则四边形为矩形.
13.【答案】
【解析】【解答】解:在矩形ABCD中,∠A=∠C=∠B=90°,AB∥CD,AD∥BC
∵EF//AD,HG//AB
∴四边形AHIE和四边形IFCG为矩形
∴HE=AI,FG=CI
∴HE+FG的长度也就是AI+CI的长度
又因为AI+CI≥AC
∴当A,I,C三点共线时,AI+CI最小,即AC的长度
在Rt△ABC中,
∴HE+FG的最小值为
故答案为:
【分析】由EF//AD,HG//AB,结合矩形的性质可得四边形AHIE和四边形IFCG为矩形,然后根据矩形的性质可的HE+FG的长度也就是AI+CI的长度,然后利用两点之间,线段最短求其最小值即可.
14.【答案】
10
【解析】【解答】解:∵四边形ABCD是矩形
∴∠BAQ=∠ABP=90°,AD=BC=40cm
设最快x秒,四边形ABPQ成为矩形,此时AQ=BP
∴3x=40-x
∴x=10
故答案为:10.
【分析】根据矩形的四个角都是直角且对边相等得出∠BAQ=∠ABP=90°,AD=BC=40cm,根据运动的观点来看,DQ=x,BP=3x,故AQ=40-x,当四边形ABPQ成为矩形时,AQ=BP,从而即可列出方程,求解即可.
三、解答题
15.【答案】
证明:∵AB=AC,D为BC边的中点,
∴AD⊥BC,BD=CD,
∴∠ADC=90°,
∵四边形ABDE是平行四边形,
∴AE∥BD,AE=BD,
∴AE∥CD,AE=CD,
∴四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴四边形ADCE是矩形
【解析】【分析】根据平行四边形的性质、利用等腰三角形的“三合一”性质推知AD⊥BC,即∠ADC=90°;由平行四边形的判定定理(对边平行且相等是四边形是平行四边形)证得四边形ADCE是平行四边形,所以有一个角是直角的平行四边形是矩形.
16.【答案】
证明:∵四边形ABDE是平行四边形,且D为BC中点
∴AE∥CD,AE=CD
∴四边形ADCE是平行四边形
又∵AB=AC,D为BC中点
∴∠ADC=90°
∴四边形ADCE是矩形
【解析】【分析】主要考查对矩形,矩形的性质,矩形的判定考点的理解.
17.【答案】
证明:∵四边形ABCD是平行四边形,
∴AO=CO=1,BO=DO=2,AB=CD=
,
∵将△ABO平移到△DCE,
∴AO=DE=1,BO=CE=2,
∴CO=DE,DO=CE,
∴四边形OCED是平行四边形,
∵CO2+DO2=1+4=5,CD2=5,
∴CO2+DO2=CD2
,
∴∠COD=90°,
∴平行四边形OCED是矩形.
【考点】矩形的判定
【解析】【分析】由平行四边形的性质可得AO=CO=1,BO=DO=2,AB=CD=
,由平移的性质可得AO=CO=DE=1,DO=CE=BO=2,可证四边形OCED是平行四边形,由勾股定理的逆定理可证∠COD=90°,可得结论.
四、综合题
18.【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形
∵DE⊥AB,∴∠DEB=90°,
∴四边形BFDE是矩形
(2)解:∵AB∥CD,
∴∠BAF=∠DFA,
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∴∠DFA=∠DAF,
∴AD=DF=5,
∵DE⊥AB,
∴∠AED=90°,由勾股定理得:DE=
=4,
∴矩形BFDE的面积=DF×DE=5×4=20.
【解析】【分析】(1)先判断四边形BFDE是平行四边形,再判断出一个角等于90°,即证明出四边形BFDE是矩形。
(2)先根据角相等得出
AD=DF,再根据勾股定理求出DE,就能求出矩形BFDE的面积.
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
初中数学湘教版八年级下册2.5.2矩形的判定
同步练习
一、单选题
1.已知四边形ABCD中AC=BD,再补充一个条件使得四边形ABCD是矩形,这个条件可以是(??
)
A.?AC⊥BD??????????????????????B.?∠ABC=90°??????????????????????C.?AC与BD互相平分??????????????????????D.?AB=BC
2.如图,在
中,对角线
与
交于点
,添加下列条件不能判定
为矩形的只有(??
)
A.???????????????B.?
,
,
??????????????C.???????????????D.?
3.如图,顺次连接四边形ABCD各边中点,得到四边形EFGH,下列条件中,可使四边形EFGH是矩形的是(????
)
A.?AB=CD?????????????????????????????B.?AC⊥BD?????????????????????????????C.?AC=BD?????????????????????????????D.?AD∥BC
4.如图,为一副重叠放置的三角板,其中∠ABC=∠EDF=90°,BC与DF共线,将△DEF沿CB方向平移,当EF经过AC的中点O时,直线EF交AB于点G,若BC=3,则此时OG的长度为(??
)
A.?3??????????????????????????????????????B.???????????????????????????????????????C.???????????????????????????????????????D.?
5.如图,在
ABCD中,AB=2
,AD=4,AC⊥BC,则△DBC比△ABC的周长长(???
)
A.?2??????????????????????????????????????????B.?4??????????????????????????????????????????C.?5??????????????????????????????????????????D.?
6.如图△ABC中,AC的垂直平分线分别交AC,AB于点D,F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是(???
)
A.?2
??????????????????????????????????????B.?3
??????????????????????????????????????C.?4??????????????????????????????????????D.?4
7.如图,为了检验教室里的矩形门框是否合格,某班的四个学习小组用三角板和细绳分别测得如下结果,其中不能判定门框是否合格的是(????
)
A.?AB=CD,AD=BC,AC=BD???????????????????????????????B.?AC=BD,∠B=∠C=90°
C.?AB=CD,∠B=∠C=90°??????????????????????????????????????D.?AB=CD,AC=BD
8.如图,有两张形状、大小完全相同的直角三角形纸片(同一个直角三角形的两条直角边不相等),把两个三角形相等的边靠在一起(两张纸片不重叠),可以拼出若干种图形,其中,形状不同的四边形有(??
)
A.?3种???????????????????????????????????????B.?4种???????????????????????????????????????C.?5种???????????????????????????????????????D.?6种
9.如图,四边形ABCD为平行四边形,延长AD到点E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是(?
)
A.?AB=BE???????????????????????????B.?BE⊥DC???????????????????????????C.?∠ADB=90°???????????????????????????D.?CE⊥DE
10.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是(??
)
A.?AB∥DC?????????????????????????????B.?AC=BD?????????????????????????????C.?AC⊥BD?????????????????????????????D.?AB=DC
二、填空题
11.如图,为了检查平行四边形书架
ABCD
的侧边是否与上、下边都垂直,工人师傅用一根绳子比较了其对角线
AC,BD
的长度,若二者长度相等,则该书架的侧边与上、下边都垂直,请你说出其中的数学原理________.
12.如图,平行四边形ABCD中,∠DAB=70°,将平行四边形ABCD变化为一个矩形(图中的虚线部分),在此过程中,分析每条边的运动.AB:________;AD:________;BC:________;CD:________.
13.如图,点E、F、G、H分别是矩形ABCD边AB、BC、CD、DA上的点,且HG与EF交于点I,连接HE、FG,若AB=6,BC=5,EF//AD,HG//AB,则HE+FG的最小值是________
.
14.如图,在矩形ABCD中,BC=40cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和1cm/s,则最快________s后,四边ABPQ成为矩形.
三、解答题
15.如图,在△ABC中,AB=AC,D为BC边的中点,以AB、BD为邻边作?ABDE,连接AD,EC.求证:四边形ADCE是矩形.
16.如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形,求证:四边形ADCE是矩形.
17.如图,
的对角线AC,
BD相交于点O,将△ABO平移到△DCE,已知AO=
1,
BO=2,
,求证:四边形OCED是矩形.
四、综合题
18.
ABCD中,过点D作DE⊥AB于点E,点F在CD上,DF=BE,连接:BF,AF。
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE-3,DF=5,求矩形BFDE的面积。
答案解析部分
一、单选题
1.【答案】
C
【解析】【解答】解:四边形ABCD中AC=BD,再补充一个条件使得四边形ABCD是矩形,这个条件可以是AC与BD互相平分,理由如下:
∵在四边形ABCD中,对角线AC,BD互相平分,
∴四边形ABCD是平行四边形,
∵AC=BD,
∴四边形ABCD是矩形.
故答案为:C.
【分析】四边形ABCD中,对角线AC,BD互相平分,得四边形ABCD是平行四边形,又由AC=BD,即可求得答案.
2.【答案】
C
【解析】【解答】解:A.
,对角线相等,可以判定
为矩形
,此选项不符合题意
;
B.
,
,
,可知△ABC为直角三角形,且∠ABC=90°,故可以判定
为矩形,此选项不符合题意
;
C.
,可以判定
为菱形,此选项符合题意
;
?
D.
,可得AO=BO,故AC=BD,可以判定
为矩形,此选项不符合题意
.
故答案为:C.
【分析】根据矩形的判定“有一个角是直角的平行四边形是矩形;对角线相等的平行四边形是矩形”即可判断求解.
3.【答案】
B
【解析】【解答】解:连接AC,BD,
∵顺次连接四边形ABCD各边中点,得到四边形EFGH,
∴EF∥HG∥AC,EH∥FG∥BD,
要使四边形EFGH为矩形,
则EF⊥EH,
故EF⊥AC,
则AC⊥BD,
故答案为:B
【分析】连接AC,BD,根据中位线的性质及矩形的判定方法即可求解.
4.【答案】
C
【解析】【解答】解:过O作OH⊥BC于H,过G作GI⊥OH于I
,
∵∠ABC=90°,
∴AB⊥BC,
∴OH∥AB,
又O为中点,
∴H为BC的中点,
∴BH=
BC=
,
∵GI⊥OH,
∴四边形BHIG为矩形,
∴GI∥BH,GI=BH=
,
又∠F=45°,
∴∠OGI=45°,
∴OG=
.
【分析】过O作OH⊥BC于H,过G作GI⊥OH于I
,根据同一平面内垂直于同一直线的两条直线互相平行得出OH∥AB,根据三角形中位线的判定定理的逆用得出H为BC的中点,故BH=
BC=
,很容易判断出四边形BHIG为矩形,根据矩形的性质得出GI∥BH,GI=BH=
,从而根据等腰直角三角形的性质得出OG的长。
5.【答案】
B
【解析】【解答】解:过点D作DG⊥BC,交BC的延长线于点G,
∵平行四边形ABCD,
∴AD=BC=4,AB=CD=
,
AD∥BC?????
∵AC⊥BC
∴AC⊥AD
∴∠CAD=∠ACG=∠DGC=90°
∴四边形ACGD是矩形,
∴AD=CG;
∴BG=BC+CG=4+4=8;
在Rt△ABC中,
在Rt△BDC中,
∴
△DBC和△ABC的周长差为
BD+BC+DC-AB-AC-BC=BD-AC=10-6=4.
故答案为:4.
【分析】过点D作DG⊥BC,交BC的延长线于点G,利用平行四边形的性质,可证得AD=BC=4,AB=CD=
,
AD∥BC,再证明四边形ACGD是矩形,根据矩形的性质,可证得AD=CG,由此可求出BG的长,然后利用勾股定理求出BD,AC的长,再求出△DBC和△ABC的周长差就是BD与AC的差,即可求出结果。
6.【答案】
A
【解析】【解答】解:∵DE是AC的垂直的平分线,F是AB的中点,
∴DF∥BC,
∴∠C=90°,
∴四边形BCDE是矩形.
∵∠A=30°,∠C=90°,BC=2,
∴AB=4,
∴AC=
=2
.
∴BE=CD=
.
∴四边形BCDE的面积为:2×
=2
.
故答案为:A.
【分析】根据三角形的中位线定理得到DF∥BC,由∠C=90°,得到四边形BCDE是矩形;根据勾股定理求出BE=CD的值,求出四边形BCDE的面积.
7.【答案】
D
【解析】【解答】A、∵AB=CD,AD=BC,∴四边形ABCD是平行四边形,
∵AC=BD,∴四边形ABCD是矩形,
故能判定门框合格;
B、在Rt△ABC和Rt△DCB中,
,
∴Rt△ABC≌Rt△DCB(HL),
∴AB=CD,
∵∠B=∠C=90°,∴AB∥CD,
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
故能判定门框合格;
C、∵∠B=∠C=90°,∴AB∥CD,
∵AB=CD,
∴四边形ABCD是平行四边形,
∵∠B=∠C=90°,
∴四边形ABCD是矩形,
故能判定门框合格;
D、当四边形ABCD是等腰梯形时,也满足AB=CD,AC=BD,故不能判定门框合格.
故答案为:D.
【分析】条件中只给出了三角板和绳子,所以可以测量四条边的长,如果对边分别相等,可以判定为平行四边形,再测量对角线,如果对角线也相等则为矩形.
8.【答案】
B
【解析】【解答】如图,①②③,
;
;
共有4种情况,两种平行四边形,矩形和一般的四边形;
故答案为:B.
【分析】根据题意将所有情况列出即可.
9.【答案】
B
【解析】【解答】解:A、∵四边形ABCD为平行四边形,∴BC∥AD,AD=BC,
∴DE=BC,
∴四边形DBCE是平行四边形(一组对边平行且相等的四边形是平行四边形),
∵AB=BE,∴△ABE是等腰三角形,
∵DE=AD,∴BD⊥DE,
∴四边形DBCE是矩形,正确,不符合题意;
B、由A知四边形DBCE是平行四边形,?
BE⊥DC?,∴四边形DBCE是菱形,错误,不符合题意.
C、由A知四边形DBCE是平行四边形,?∵∠ADB=90°
,∴四边形DBCE是矩形,正确,不符合题意;
D、由A知四边形DBCE是平行四边形,?∵CE⊥DE,∠DEC=90°
,∴四边形DBCE是矩形,正确,不符合题意;
故答案为:B.
【分析】由平行四边形的性质,结合DE=AD,可证四边形DBCE是平行四边形,由于AB=CE,利用等腰三角形的性质可得BD⊥DE,则由一个角是直角的平行四边形是矩形可证四边形DBCE是矩形;CD都可依据一个角是直角的平行四边形是矩形可证四边形DBCE是矩形;而B项对角线互相垂直只能得出四边形DBCE是菱形.
10.【答案】
C
【解析】【解答】解:依题意得,四边形EFGH是由四边形ABCD各边中点连接而成,
连接AC、BD,
故EF∥AC∥HG,EH∥BD∥FG,
所以四边形EFGH是平行四边形,
要使四边形EFGH为矩形,
根据矩形的判定(有一个角为直角的平行四边形是矩形)
故当AC⊥BD时,∠EFG=∠EHG=90度.四边形EFGH为矩形.
故选C.
【分析】根据矩形的判定定理(有一个角为直角的平行四边形是矩形).先证四边形EFGH是平行四边形,要使四边形EFGH为矩形,需要∠EFG=90度.由此推出AC⊥BD.
二、填空题
11.【答案】
对角线相等的平行四边形是矩形,矩形的四个角都是直角;
【解析】【解答】因为平行四边形ABCD的对角线相等,所以四边形ABCD是矩形,而矩形的四个角都是直角.
故答案是:对角线相等的平行四边形是矩形,矩形的四个角都是直角
【分析】根据矩形的判定和性质定理,即可解答.
12.【答案】
不动;绕点A沿逆时针旋转20°;绕点B沿逆时针旋转20°;平移
【解析】【解答】ABCD是平行四边形,两组对边分别平行,只要保证一个角为90°,则四边形ABCD即为矩形.
【分析】熟练掌握矩形的判定.平行四边形只要保证一个角为直角,则四边形为矩形.
13.【答案】
【解析】【解答】解:在矩形ABCD中,∠A=∠C=∠B=90°,AB∥CD,AD∥BC
∵EF//AD,HG//AB
∴四边形AHIE和四边形IFCG为矩形
∴HE=AI,FG=CI
∴HE+FG的长度也就是AI+CI的长度
又因为AI+CI≥AC
∴当A,I,C三点共线时,AI+CI最小,即AC的长度
在Rt△ABC中,
∴HE+FG的最小值为
故答案为:
【分析】由EF//AD,HG//AB,结合矩形的性质可得四边形AHIE和四边形IFCG为矩形,然后根据矩形的性质可的HE+FG的长度也就是AI+CI的长度,然后利用两点之间,线段最短求其最小值即可.
14.【答案】
10
【解析】【解答】解:∵四边形ABCD是矩形
∴∠BAQ=∠ABP=90°,AD=BC=40cm
设最快x秒,四边形ABPQ成为矩形,此时AQ=BP
∴3x=40-x
∴x=10
故答案为:10.
【分析】根据矩形的四个角都是直角且对边相等得出∠BAQ=∠ABP=90°,AD=BC=40cm,根据运动的观点来看,DQ=x,BP=3x,故AQ=40-x,当四边形ABPQ成为矩形时,AQ=BP,从而即可列出方程,求解即可.
三、解答题
15.【答案】
证明:∵AB=AC,D为BC边的中点,
∴AD⊥BC,BD=CD,
∴∠ADC=90°,
∵四边形ABDE是平行四边形,
∴AE∥BD,AE=BD,
∴AE∥CD,AE=CD,
∴四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴四边形ADCE是矩形
【解析】【分析】根据平行四边形的性质、利用等腰三角形的“三合一”性质推知AD⊥BC,即∠ADC=90°;由平行四边形的判定定理(对边平行且相等是四边形是平行四边形)证得四边形ADCE是平行四边形,所以有一个角是直角的平行四边形是矩形.
16.【答案】
证明:∵四边形ABDE是平行四边形,且D为BC中点
∴AE∥CD,AE=CD
∴四边形ADCE是平行四边形
又∵AB=AC,D为BC中点
∴∠ADC=90°
∴四边形ADCE是矩形
【解析】【分析】主要考查对矩形,矩形的性质,矩形的判定考点的理解.
17.【答案】
证明:∵四边形ABCD是平行四边形,
∴AO=CO=1,BO=DO=2,AB=CD=
,
∵将△ABO平移到△DCE,
∴AO=DE=1,BO=CE=2,
∴CO=DE,DO=CE,
∴四边形OCED是平行四边形,
∵CO2+DO2=1+4=5,CD2=5,
∴CO2+DO2=CD2
,
∴∠COD=90°,
∴平行四边形OCED是矩形.
【考点】矩形的判定
【解析】【分析】由平行四边形的性质可得AO=CO=1,BO=DO=2,AB=CD=
,由平移的性质可得AO=CO=DE=1,DO=CE=BO=2,可证四边形OCED是平行四边形,由勾股定理的逆定理可证∠COD=90°,可得结论.
四、综合题
18.【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形
∵DE⊥AB,∴∠DEB=90°,
∴四边形BFDE是矩形
(2)解:∵AB∥CD,
∴∠BAF=∠DFA,
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∴∠DFA=∠DAF,
∴AD=DF=5,
∵DE⊥AB,
∴∠AED=90°,由勾股定理得:DE=
=4,
∴矩形BFDE的面积=DF×DE=5×4=20.
【解析】【分析】(1)先判断四边形BFDE是平行四边形,再判断出一个角等于90°,即证明出四边形BFDE是矩形。
(2)先根据角相等得出
AD=DF,再根据勾股定理求出DE,就能求出矩形BFDE的面积.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
