数学:《坐标方法的简单应用》同步练习2(人教版七年级下)
文档属性
| 名称 | 数学:《坐标方法的简单应用》同步练习2(人教版七年级下) |

|
|
| 格式 | zip | ||
| 文件大小 | 593.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-14 00:00:00 | ||
图片预览


文档简介
数学:《坐标方法的简单应用》同步练习2(人教版七年级下)
5分钟训练(预习类训练,可用于课前)
1.如果点A既在x轴的上方,又在y轴的左边,且距离x轴、y轴分别为5、4个单位,那么A点的坐标为( )
A.(5,-4) B.(4,-5) C.(-5,4) D.(-4,5)
解析:点A在x轴的上方,则纵坐标大于零;在y轴的左边横坐标小于零.
答案:C
2.小华若将直角坐标系中的一只猫的图案向左平移了3个单位长度,而猫的形状、大小都不变,则图案上各点的坐标的变化情况为( )
A.横坐标加3,纵坐标不变 B.纵坐标加3,横坐标不变
C.横坐标减小3,纵坐标不变 D.纵坐标减小3,横坐标不变
解析:若将直角坐标系中的一个图案左、右平移,而图案的形状、大小都不变,只需将原图案的横坐标加或减去一个值,纵坐标不变.
答案:C
3.若将直角坐标系中的一只鱼的图案向下平移了3个单位长度,而鱼的形状、大小都不变,则图案上各点的坐标的变化情况为( )
A.横坐标加3,纵坐标不变 B.纵坐标加3,横坐标不变
C.横坐标减小3,纵坐标不变 D.纵坐标减小3,横坐标不变
解析:若将直角坐标系中的一个图案上、下平移,而图案的形状、大小都不变,只需将原图案的纵坐标加或减去一个值,横坐标不变.
答案:D
4.在平面内,将一个图形沿_____________移动_____________,这样的图形移动称为平移.平移前后两个图形的_____________和_____________不变.
答案:某个方向 一定的距离 形状 大小
10分钟训练(强化类训练,可用于课中)
1.(2010浙江温州模拟,5)点A(1,2)向右平移2个单位得到对应点A′,则点A′的坐标是( )
A.(1,4) B.(1,0) C.(-1,2) D.(3,2)
解析:向左右平移各点的纵坐标不变,横坐标增加.
答案:D
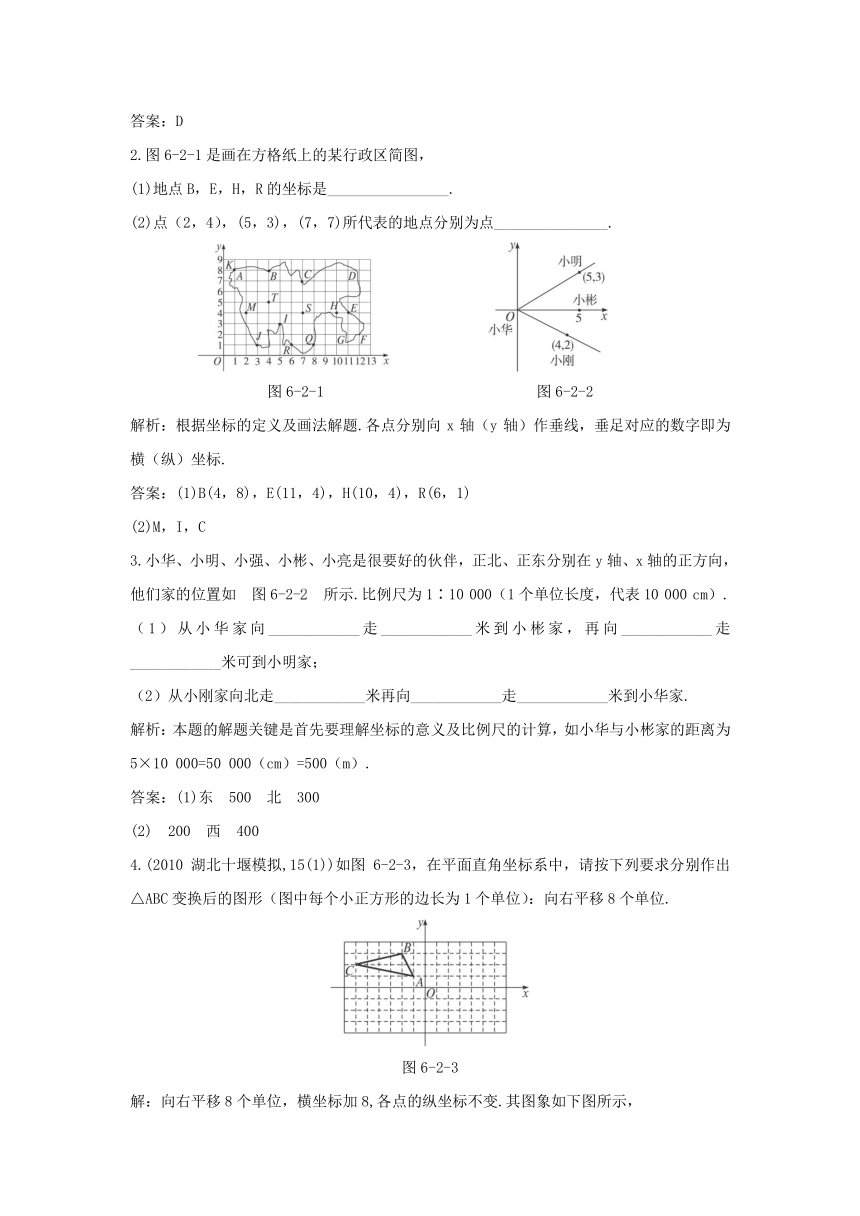
2.图6-2-1是画在方格纸上的某行政区简图,
(1)地点B,E,H,R的坐标是________________.
(2)点(2,4),(5,3),(7,7)所代表的地点分别为点_______________.
图6-2-1 图6-2-2
解析:根据坐标的定义及画法解题.各点分别向x轴(y轴)作垂线,垂足对应的数字即为横(纵)坐标.
答案:(1)B(4,8),E(11,4),H(10,4),R(6,1)
(2)M,I,C
3.小华、小明、小强、小彬、小亮是很要好的伙伴,正北、正东分别在y轴、x轴的正方向,他们家的位置如?图6-2-2?所示.比例尺为1∶10 000(1个单位长度,代表10 000 cm).
(1)从小华家向____________走____________米到小彬家,再向____________走____________米可到小明家;
(2)从小刚家向北走____________米再向____________走____________米到小华家.
解析:本题的解题关键是首先要理解坐标的意义及比例尺的计算,如小华与小彬家的距离为5×10 000=50 000(cm)=500(m).
答案:(1)东 500 北 300
(2) 200 西 400
4.(2010湖北十堰模拟,15(1))如图6-2-3,在平面直角坐标系中,请按下列要求分别作出△ABC变换后的图形(图中每个小正方形的边长为1个单位):向右平移8个单位.
图6-2-3
解:向右平移8个单位,横坐标加8,各点的纵坐标不变.其图象如下图所示,
5.在上一个题目中若△ABC内有一个点M(a,b),平移后其坐标变成什么?
解:△ABC向右平移8个单位,点?M(a,b)也跟着平移,平移后其坐标变成(a+8,b).
6.在直角坐标系中描出下列各点(-1,-2),(0,0),(2,4),并顺次连结各点观察其形状特点,点(1,2)是否在它们的连线上?
解:如图所示,是一条直线;点(1,2)在这条直线上.
30分钟训练(巩固类训练,可用于课后)
1.如果长方形的三个顶点的坐标分别为(-3,2),(3,2),(3,-2),则这个长方形的面积为( )
A.32 B.24 C.6 D.8
解析:如图所示,长方形的长为6,宽为4,所以面积为24.
答案:B
2.(1)小明在直角坐标系中画出了一个长方形,他想把这个长方形向右平移3个单位长度,再向上平移2个单位长度,所得图形与原图形相比_______________;
(2)若他将此长方形的横坐标都不变,纵坐标变为原来的,则所得的长方形与原长方形相比_____________.
解析:(1)在变化过程中,横坐标分别加3,纵坐标加2即可;(2)若将此长方形的横坐标都不变,纵坐标变为原来的,则所得的长方形与原长方形相比,图案横向未发生改变,纵向被压缩为原来的一半;
答案:(1)横坐标分别加3,纵坐标加2
(2)横向未发生改变,纵向压缩为原来的一半
3.将一梯形的各顶点的横坐标变为原来的2倍,纵坐标变为原来的,则所得图形的面积与原来图形的面积_____________.
解析:将一梯形的各顶点的横坐标变为原来的2倍,所得的梯形与原梯形相比,图案纵向未发生改变,纵坐标没变,整个图形横向拉长为原来2倍,则面积是原梯形面积的2倍;再将该梯形的各顶点的纵坐标变为原来的,图案纵向未发生改变,纵向被压缩为原来的一半,即面积又缩小为新梯形的.综上所述,所得图形的面积与原来图形的面积相等.
答案:相等
4.在平面直角坐标系中,(1)将坐标为(0,0),(2,4),(2,0),(4,4)的点用线段依次连结起来形成一个图案.(2)若横坐标保持不变,纵坐标分别加3呢?
解:(1)下图虚线即为所求;
(2)横坐标保持不变,纵坐标分别加3,相当于把原图案向上平移了3个单位,所以其形状、大小都不发生改变.
5.(2010海南模拟,21(2))△ABC在平面直角坐标系中的位置如图6-2-4所示.
将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标.
图6-2-4
分析:△ABC向右平移6个单位,各点的纵坐标不变,横坐标加6.
解:(1)如图所示,
(2)△ABC中点的坐标分别是A(0,4)、B(-2,2)、C(-1,1);所以A2(6,4),B2(4,2),C2(5,1).
6.小明头顶上方A处5 000米的高空有一架飞机飞过,飞机的速度为300米/秒,若飞行方向不变,飞行10秒后来到B处,用1∶100 000的比例尺,你能否用直角坐标系来表示飞机前后A、B的坐标,通过测量试求出小明与B点的大概距离.
解:以小明为原点竖直方向为纵轴,飞行方向为横轴建立如图所示的直角坐标系,则A(0,5),B(3,5).经过测量图中OB约为5.8 cm,所以根据公式:比例尺=,可求得小明与B点的大概距离为5.8×100 000=5 800(米).
7.(1)在直角坐标系中描出下列各点A(2,1),B(-2,1),C(3,2),D(-3,2);
(2)连结AB、CD观察它们与y轴的关系,
(3)猜想(a,1)(-a,1)两点的连线是否遵循上述规律.
解:(1)描点如图所示;
(2)y轴是AB、CD的垂直平分线;
(3)已知点的坐标规律是A与B,C与D的横坐标互为相反数纵坐标相同;点(a,1),?(-a,1)具备上述规律,所以y轴是(a,1)、(?-a,1)两点的连线的垂直平分线.
8.图6-2-5是游乐城的平面示意图,借助刻度尺、量角器,解决如下问题:
图6-2-5
(1)建立适当的平面直角坐标系,写出各景点的坐标.
(2)用量角器量出海底世界位于入口处的什么方向,在同一方向上还有什么景点
(3)用刻度尺量出球幕电影到入口处的图上距离,并求出它们的实际距离.
解:(1)答案不唯一.若以“海底世界”为原点,则入口处(4,-1);童趣花园(4,2);梦幻艺馆(1,3);球幕电影(2,-4);
(2)海底世界位于入口处北偏西约76°,在同一方向上还有太空秋千;
(3)球幕电影到入口处图上距离约为1. 8 cm,实际距离为1.8÷=270(米).
9.如图6-2-6所示,在直角坐标系下,图(1)中的图案“A”经过变换分别变成图(2)至图(6)中的相应图案(虚线对应于原图案),试写出图(2)至图(6)中各顶点的坐标,探索每次变换前后图案发生了什么变化,对应点的坐标之间有什么关系.
(1) (2) (3)
(4) (5) (6)
图6-2-6
解:由题图可知.由图(1)到图(2)是横坐标变为原来的2倍,纵坐标没变,整个图形横向拉长为原来2倍.
由图(1)到图(3)是横坐标都加3,纵坐标不变,整个图形整体向右移动3个单位.
由图(1)到图(4)是横坐标不变,纵坐标都乘以-1,两个图形的大小和形状相同.
由图(1)到图(5)是横坐标不变,纵坐标变为原来的2倍,图形被纵向拉长为原来的2倍.
由图(1)到图(6)是横坐标、纵坐标都变为原来的2倍,形状不变,大小放大为原来的4倍.
5分钟训练(预习类训练,可用于课前)
1.如果点A既在x轴的上方,又在y轴的左边,且距离x轴、y轴分别为5、4个单位,那么A点的坐标为( )
A.(5,-4) B.(4,-5) C.(-5,4) D.(-4,5)
解析:点A在x轴的上方,则纵坐标大于零;在y轴的左边横坐标小于零.
答案:C
2.小华若将直角坐标系中的一只猫的图案向左平移了3个单位长度,而猫的形状、大小都不变,则图案上各点的坐标的变化情况为( )
A.横坐标加3,纵坐标不变 B.纵坐标加3,横坐标不变
C.横坐标减小3,纵坐标不变 D.纵坐标减小3,横坐标不变
解析:若将直角坐标系中的一个图案左、右平移,而图案的形状、大小都不变,只需将原图案的横坐标加或减去一个值,纵坐标不变.
答案:C
3.若将直角坐标系中的一只鱼的图案向下平移了3个单位长度,而鱼的形状、大小都不变,则图案上各点的坐标的变化情况为( )
A.横坐标加3,纵坐标不变 B.纵坐标加3,横坐标不变
C.横坐标减小3,纵坐标不变 D.纵坐标减小3,横坐标不变
解析:若将直角坐标系中的一个图案上、下平移,而图案的形状、大小都不变,只需将原图案的纵坐标加或减去一个值,横坐标不变.
答案:D
4.在平面内,将一个图形沿_____________移动_____________,这样的图形移动称为平移.平移前后两个图形的_____________和_____________不变.
答案:某个方向 一定的距离 形状 大小
10分钟训练(强化类训练,可用于课中)
1.(2010浙江温州模拟,5)点A(1,2)向右平移2个单位得到对应点A′,则点A′的坐标是( )
A.(1,4) B.(1,0) C.(-1,2) D.(3,2)
解析:向左右平移各点的纵坐标不变,横坐标增加.
答案:D
2.图6-2-1是画在方格纸上的某行政区简图,
(1)地点B,E,H,R的坐标是________________.
(2)点(2,4),(5,3),(7,7)所代表的地点分别为点_______________.
图6-2-1 图6-2-2
解析:根据坐标的定义及画法解题.各点分别向x轴(y轴)作垂线,垂足对应的数字即为横(纵)坐标.
答案:(1)B(4,8),E(11,4),H(10,4),R(6,1)
(2)M,I,C
3.小华、小明、小强、小彬、小亮是很要好的伙伴,正北、正东分别在y轴、x轴的正方向,他们家的位置如?图6-2-2?所示.比例尺为1∶10 000(1个单位长度,代表10 000 cm).
(1)从小华家向____________走____________米到小彬家,再向____________走____________米可到小明家;
(2)从小刚家向北走____________米再向____________走____________米到小华家.
解析:本题的解题关键是首先要理解坐标的意义及比例尺的计算,如小华与小彬家的距离为5×10 000=50 000(cm)=500(m).
答案:(1)东 500 北 300
(2) 200 西 400
4.(2010湖北十堰模拟,15(1))如图6-2-3,在平面直角坐标系中,请按下列要求分别作出△ABC变换后的图形(图中每个小正方形的边长为1个单位):向右平移8个单位.
图6-2-3
解:向右平移8个单位,横坐标加8,各点的纵坐标不变.其图象如下图所示,
5.在上一个题目中若△ABC内有一个点M(a,b),平移后其坐标变成什么?
解:△ABC向右平移8个单位,点?M(a,b)也跟着平移,平移后其坐标变成(a+8,b).
6.在直角坐标系中描出下列各点(-1,-2),(0,0),(2,4),并顺次连结各点观察其形状特点,点(1,2)是否在它们的连线上?
解:如图所示,是一条直线;点(1,2)在这条直线上.
30分钟训练(巩固类训练,可用于课后)
1.如果长方形的三个顶点的坐标分别为(-3,2),(3,2),(3,-2),则这个长方形的面积为( )
A.32 B.24 C.6 D.8
解析:如图所示,长方形的长为6,宽为4,所以面积为24.
答案:B
2.(1)小明在直角坐标系中画出了一个长方形,他想把这个长方形向右平移3个单位长度,再向上平移2个单位长度,所得图形与原图形相比_______________;
(2)若他将此长方形的横坐标都不变,纵坐标变为原来的,则所得的长方形与原长方形相比_____________.
解析:(1)在变化过程中,横坐标分别加3,纵坐标加2即可;(2)若将此长方形的横坐标都不变,纵坐标变为原来的,则所得的长方形与原长方形相比,图案横向未发生改变,纵向被压缩为原来的一半;
答案:(1)横坐标分别加3,纵坐标加2
(2)横向未发生改变,纵向压缩为原来的一半
3.将一梯形的各顶点的横坐标变为原来的2倍,纵坐标变为原来的,则所得图形的面积与原来图形的面积_____________.
解析:将一梯形的各顶点的横坐标变为原来的2倍,所得的梯形与原梯形相比,图案纵向未发生改变,纵坐标没变,整个图形横向拉长为原来2倍,则面积是原梯形面积的2倍;再将该梯形的各顶点的纵坐标变为原来的,图案纵向未发生改变,纵向被压缩为原来的一半,即面积又缩小为新梯形的.综上所述,所得图形的面积与原来图形的面积相等.
答案:相等
4.在平面直角坐标系中,(1)将坐标为(0,0),(2,4),(2,0),(4,4)的点用线段依次连结起来形成一个图案.(2)若横坐标保持不变,纵坐标分别加3呢?
解:(1)下图虚线即为所求;
(2)横坐标保持不变,纵坐标分别加3,相当于把原图案向上平移了3个单位,所以其形状、大小都不发生改变.
5.(2010海南模拟,21(2))△ABC在平面直角坐标系中的位置如图6-2-4所示.
将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标.
图6-2-4
分析:△ABC向右平移6个单位,各点的纵坐标不变,横坐标加6.
解:(1)如图所示,
(2)△ABC中点的坐标分别是A(0,4)、B(-2,2)、C(-1,1);所以A2(6,4),B2(4,2),C2(5,1).
6.小明头顶上方A处5 000米的高空有一架飞机飞过,飞机的速度为300米/秒,若飞行方向不变,飞行10秒后来到B处,用1∶100 000的比例尺,你能否用直角坐标系来表示飞机前后A、B的坐标,通过测量试求出小明与B点的大概距离.
解:以小明为原点竖直方向为纵轴,飞行方向为横轴建立如图所示的直角坐标系,则A(0,5),B(3,5).经过测量图中OB约为5.8 cm,所以根据公式:比例尺=,可求得小明与B点的大概距离为5.8×100 000=5 800(米).
7.(1)在直角坐标系中描出下列各点A(2,1),B(-2,1),C(3,2),D(-3,2);
(2)连结AB、CD观察它们与y轴的关系,
(3)猜想(a,1)(-a,1)两点的连线是否遵循上述规律.
解:(1)描点如图所示;
(2)y轴是AB、CD的垂直平分线;
(3)已知点的坐标规律是A与B,C与D的横坐标互为相反数纵坐标相同;点(a,1),?(-a,1)具备上述规律,所以y轴是(a,1)、(?-a,1)两点的连线的垂直平分线.
8.图6-2-5是游乐城的平面示意图,借助刻度尺、量角器,解决如下问题:
图6-2-5
(1)建立适当的平面直角坐标系,写出各景点的坐标.
(2)用量角器量出海底世界位于入口处的什么方向,在同一方向上还有什么景点
(3)用刻度尺量出球幕电影到入口处的图上距离,并求出它们的实际距离.
解:(1)答案不唯一.若以“海底世界”为原点,则入口处(4,-1);童趣花园(4,2);梦幻艺馆(1,3);球幕电影(2,-4);
(2)海底世界位于入口处北偏西约76°,在同一方向上还有太空秋千;
(3)球幕电影到入口处图上距离约为1. 8 cm,实际距离为1.8÷=270(米).
9.如图6-2-6所示,在直角坐标系下,图(1)中的图案“A”经过变换分别变成图(2)至图(6)中的相应图案(虚线对应于原图案),试写出图(2)至图(6)中各顶点的坐标,探索每次变换前后图案发生了什么变化,对应点的坐标之间有什么关系.
(1) (2) (3)
(4) (5) (6)
图6-2-6
解:由题图可知.由图(1)到图(2)是横坐标变为原来的2倍,纵坐标没变,整个图形横向拉长为原来2倍.
由图(1)到图(3)是横坐标都加3,纵坐标不变,整个图形整体向右移动3个单位.
由图(1)到图(4)是横坐标不变,纵坐标都乘以-1,两个图形的大小和形状相同.
由图(1)到图(5)是横坐标不变,纵坐标变为原来的2倍,图形被纵向拉长为原来的2倍.
由图(1)到图(6)是横坐标、纵坐标都变为原来的2倍,形状不变,大小放大为原来的4倍.
