6.1.1 平行四边形的性质 课件(共15张PPT)
文档属性
| 名称 | 6.1.1 平行四边形的性质 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 06:09:23 | ||
图片预览



文档简介
数学北师大版
八年级下
6.1平行四边形的性质(第1课时)
生活中见到的平行四边形
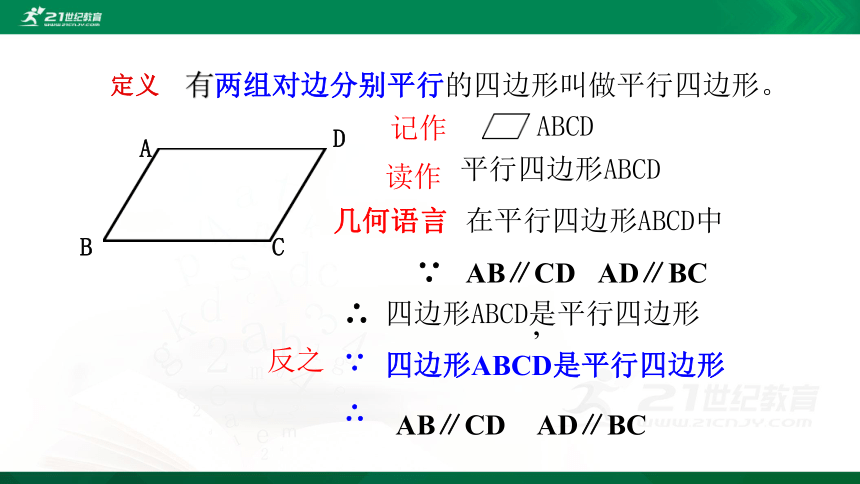
定义
有两组对边分别平行的四边形叫做平行四边形。
A
D
B
C
记作
ABCD
读作
平行四边形ABCD
几何语言
在平行四边形ABCD中
∵
AB∥CD
,
AD∥BC
反之
∵
四边形ABCD是平行四边形
∴
AB∥CD
AD∥BC
∴
四边形ABCD是平行四边形
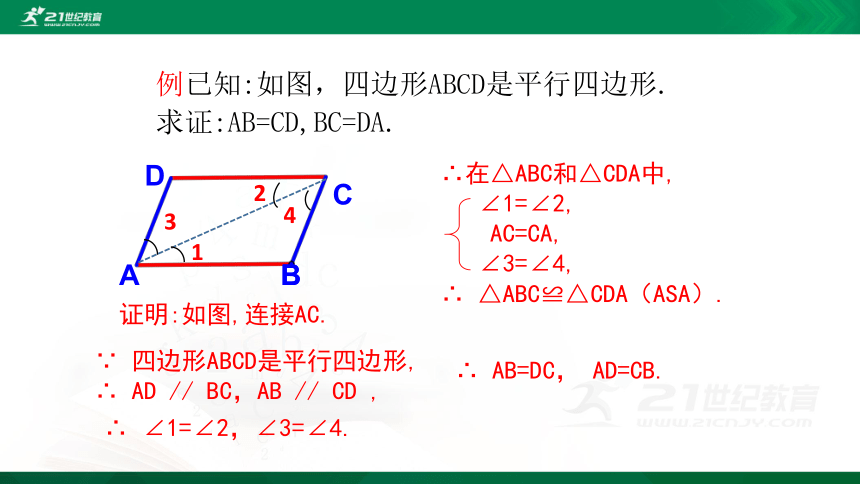
例已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
A
B
C
B
D
证明:如图,连接AC.
∵ 四边形ABCD是平行四边形,
∴ AD // BC,AB // CD ,
∴ ∠1=∠2,∠3=∠4.
1
2
3
4
∴在△ABC和△CDA中,
∠1=∠2,
AC=CA,
∠3=∠4,
∴ △ABC≌△CDA(ASA).
∴ AB=DC, AD=CB.
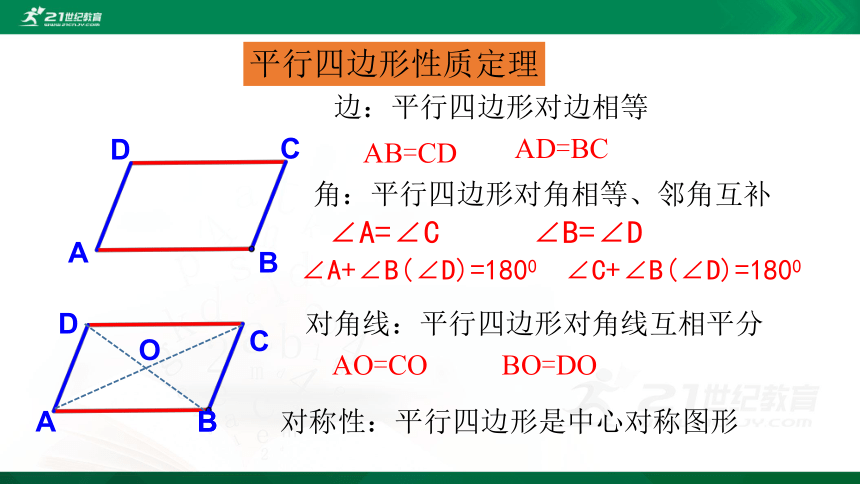
平行四边形性质定理
边:平行四边形对边相等
角:平行四边形对角相等、邻角互补
对角线:平行四边形对角线互相平分
对称性:平行四边形是中心对称图形
A
B
C
D
AB=CD
AD=BC
A
B
C
B
D
∠A=∠C
∠B=∠D
∠A+∠B(∠D)=1800
∠C+∠B(∠D)=1800
O
AO=CO
BO=DO
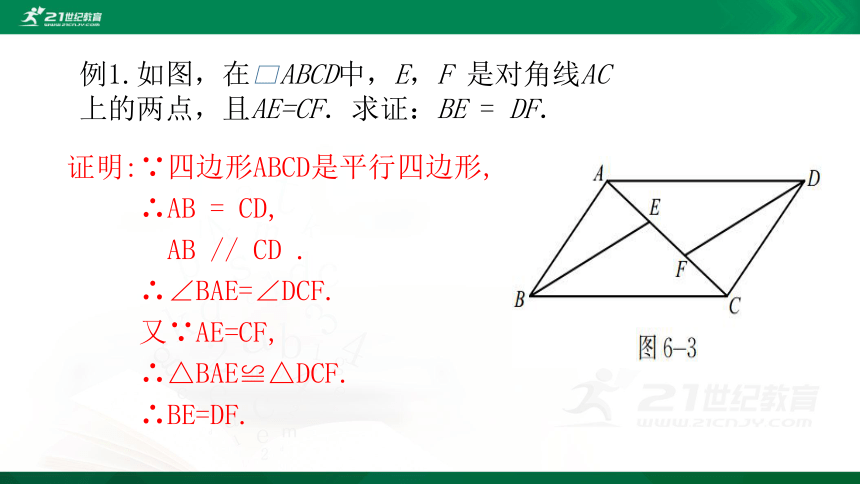
例1.如图,在 ABCD中,E,F 是对角线AC
上的两点,且AE=CF.求证:BE = DF.
证明:∵四边形ABCD是平行四边形,
∴AB = CD,
AB // CD .
∴∠BAE=∠DCF.
又∵AE=CF,
∴△BAE≌△DCF.
∴BE=DF.
基础训练
平行四边形的周长等于相邻两边长和的2倍
1、在 ABCD中 ,若∠A:∠B=5:4,
则∠C= ,∠D= .
2、若 ABCD的周长为18cm, AB=4cm ,
则BC= .
100°
80°
5cm
3.如图,已知 ABCD 中,AD=3,BD⊥AD, 且BD=4, 你能求出平行四边形的周长吗?
A
D
C
B
4
3
解: ∵BD ⊥AD
∴ ∠ADB=90 °
在Rt △ADB中,AD=3,BD=4
∴AB= = 5(勾股定理)
又∵四边形ABCD为平行四边形(已知)
∴ AD=BC=3
AB=DC=5
∴ ABCD的周长=2(AD+AB)
=2(3+5) =16
练习1 如图: ABCD的周长为36,由钝角顶点D分别向AB,BC引两条高DE,DF,且DE=4 ,DF=5,求这个平行四边形的面积 .
∟
∟
A
E
B
F
C
D
平行四边形的面积S=AB×DE=BC×DF
S=4AB=5BC
∴S=40
∴
∴
3△ABC是等腰三角形, AB=AC, P是底边BC上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB上.求证 :PE+PF=AB
A
F
证明:因为PE∥AB,PF∥AC
∴四边形AFPE为平行四边形.
∴AF=PE,∠BPF=∠C
又因为AB=AC
∴
∠B=∠C
∴∠BPF=∠B
∴BF=PF
∴PE+PF=AF+BF=AB
思考:学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
A
B
C
1.如图,在?ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O.求证:OA=OE.
证明:由折叠以及平行四边形的性质可得∠DBE=∠DBC=∠ADB,∠A=∠C=∠E,
∴OB=OD,∠A=∠C=∠E,
∴△AOB≌△EOD( AAS ), ∴OA=OE.
课后作业
在△AOB和△EOD中,
∠A=∠E,
∠AOB=∠EOD,
OB=OD
2.如图,在?ABCD中,DE=CE,连接AE并延长交BC的延长线于点F. ( 1 )求证:△ADE≌△FCE; ( 2 )若AB=2BC,∠F=36°.求∠B的度数.
∴△ADE≌△FCE( ASA ).
解:( 1 )∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠D=∠ECF,
在△ADE和△FCE中,
∴∠B=180°-2×36°=108°.
∴∠BAF=∠F=36°,
∵AB=2BC,∴AB=FB,
∵AD=BC,∴FC=BC,
∴AD=FC,
( 2 )∵△ADE≌△FCE,
∠D=∠ECF,
DE=CE
∠AED=∠FEC,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
八年级下
6.1平行四边形的性质(第1课时)
生活中见到的平行四边形
定义
有两组对边分别平行的四边形叫做平行四边形。
A
D
B
C
记作
ABCD
读作
平行四边形ABCD
几何语言
在平行四边形ABCD中
∵
AB∥CD
,
AD∥BC
反之
∵
四边形ABCD是平行四边形
∴
AB∥CD
AD∥BC
∴
四边形ABCD是平行四边形
例已知:如图,四边形ABCD是平行四边形.
求证:AB=CD,BC=DA.
A
B
C
B
D
证明:如图,连接AC.
∵ 四边形ABCD是平行四边形,
∴ AD // BC,AB // CD ,
∴ ∠1=∠2,∠3=∠4.
1
2
3
4
∴在△ABC和△CDA中,
∠1=∠2,
AC=CA,
∠3=∠4,
∴ △ABC≌△CDA(ASA).
∴ AB=DC, AD=CB.
平行四边形性质定理
边:平行四边形对边相等
角:平行四边形对角相等、邻角互补
对角线:平行四边形对角线互相平分
对称性:平行四边形是中心对称图形
A
B
C
D
AB=CD
AD=BC
A
B
C
B
D
∠A=∠C
∠B=∠D
∠A+∠B(∠D)=1800
∠C+∠B(∠D)=1800
O
AO=CO
BO=DO
例1.如图,在 ABCD中,E,F 是对角线AC
上的两点,且AE=CF.求证:BE = DF.
证明:∵四边形ABCD是平行四边形,
∴AB = CD,
AB // CD .
∴∠BAE=∠DCF.
又∵AE=CF,
∴△BAE≌△DCF.
∴BE=DF.
基础训练
平行四边形的周长等于相邻两边长和的2倍
1、在 ABCD中 ,若∠A:∠B=5:4,
则∠C= ,∠D= .
2、若 ABCD的周长为18cm, AB=4cm ,
则BC= .
100°
80°
5cm
3.如图,已知 ABCD 中,AD=3,BD⊥AD, 且BD=4, 你能求出平行四边形的周长吗?
A
D
C
B
4
3
解: ∵BD ⊥AD
∴ ∠ADB=90 °
在Rt △ADB中,AD=3,BD=4
∴AB= = 5(勾股定理)
又∵四边形ABCD为平行四边形(已知)
∴ AD=BC=3
AB=DC=5
∴ ABCD的周长=2(AD+AB)
=2(3+5) =16
练习1 如图: ABCD的周长为36,由钝角顶点D分别向AB,BC引两条高DE,DF,且DE=4 ,DF=5,求这个平行四边形的面积 .
∟
∟
A
E
B
F
C
D
平行四边形的面积S=AB×DE=BC×DF
S=4AB=5BC
∴S=40
∴
∴
3△ABC是等腰三角形, AB=AC, P是底边BC上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB上.求证 :PE+PF=AB
A
F
证明:因为PE∥AB,PF∥AC
∴四边形AFPE为平行四边形.
∴AF=PE,∠BPF=∠C
又因为AB=AC
∴
∠B=∠C
∴∠BPF=∠B
∴BF=PF
∴PE+PF=AF+BF=AB
思考:学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
A
B
C
1.如图,在?ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O.求证:OA=OE.
证明:由折叠以及平行四边形的性质可得∠DBE=∠DBC=∠ADB,∠A=∠C=∠E,
∴OB=OD,∠A=∠C=∠E,
∴△AOB≌△EOD( AAS ), ∴OA=OE.
课后作业
在△AOB和△EOD中,
∠A=∠E,
∠AOB=∠EOD,
OB=OD
2.如图,在?ABCD中,DE=CE,连接AE并延长交BC的延长线于点F. ( 1 )求证:△ADE≌△FCE; ( 2 )若AB=2BC,∠F=36°.求∠B的度数.
∴△ADE≌△FCE( ASA ).
解:( 1 )∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠D=∠ECF,
在△ADE和△FCE中,
∴∠B=180°-2×36°=108°.
∴∠BAF=∠F=36°,
∵AB=2BC,∴AB=FB,
∵AD=BC,∴FC=BC,
∴AD=FC,
( 2 )∵△ADE≌△FCE,
∠D=∠ECF,
DE=CE
∠AED=∠FEC,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
