6.2.1 平行四边形的判定 课件(共18张PPT)
文档属性
| 名称 | 6.2.1 平行四边形的判定 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 00:00:00 | ||
图片预览


文档简介
数学北师大版
八年级下
6.2平行四边形的判定第1课时
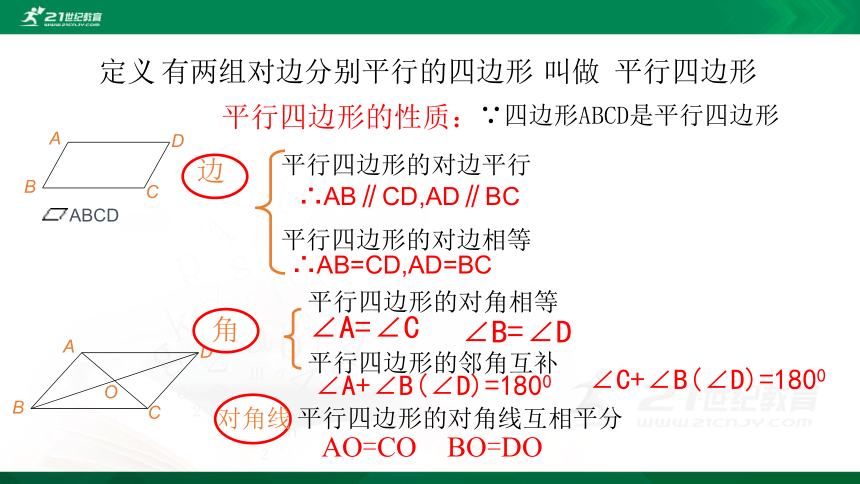
有两组对边分别平行的四边形
叫做
平行四边形
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
∴AB∥CD,AD∥BC
定义
∠A+∠B(∠D)=1800
∠A=∠C
∠B=∠D
∠C+∠B(∠D)=1800
AO=CO
BO=DO
判定定理1:两组对边相等的四边形是平行四边形
已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
B
C
A
D
证明:连结AC,
∵ AB=CD,AD=BC (已知)
又∵ AC=AC (公共边)
∴△ABC≌△CDA(SSS)
1
1
2
∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形
3
4
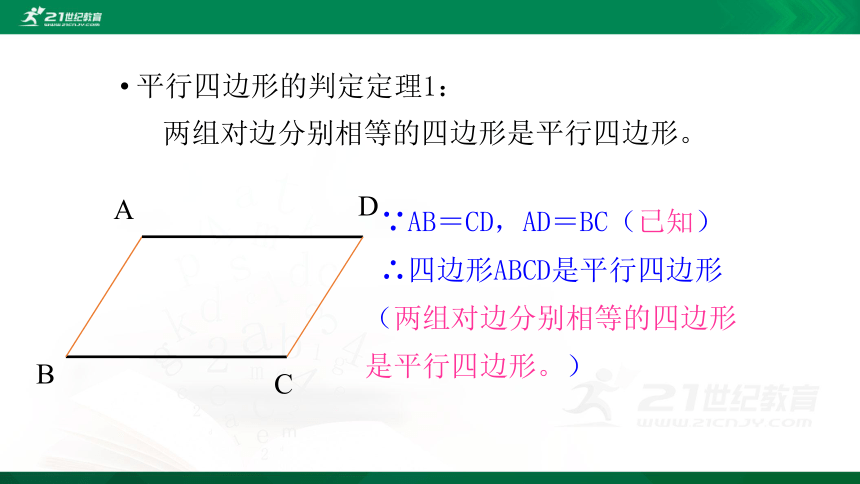
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形。)
B
C
A
D
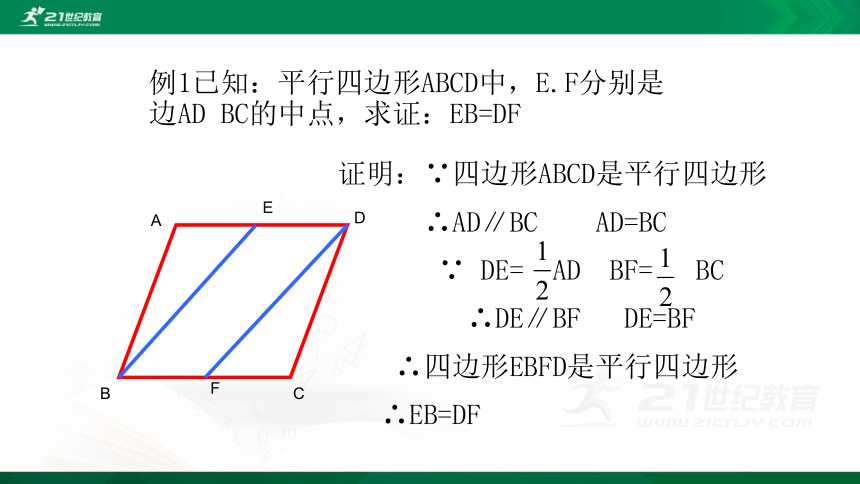
例1已知:平行四边形ABCD中,E.F分别是边AD BC的中点,求证:EB=DF
A
C
D
E
F
B
证明:∵四边形ABCD是平行四边形
∴AD∥BC AD=BC
∵ DE= AD BF= BC
∴DE∥BF DE=BF
∴四边形EBFD是平行四边形
∴EB=DF
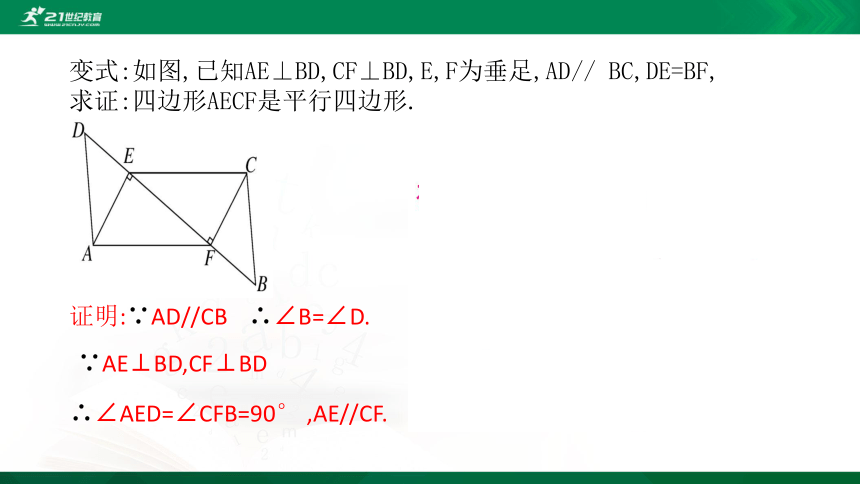
变式:如图,已知AE⊥BD,CF⊥BD,E,F为垂足,AD// BC,DE=BF,求证:四边形AECF是平行四边形.
证明:∵AD//CB
∴∠B=∠D.
∴∠AED=∠CFB=90° ,AE//CF.
∵AE⊥BD,CF⊥BD
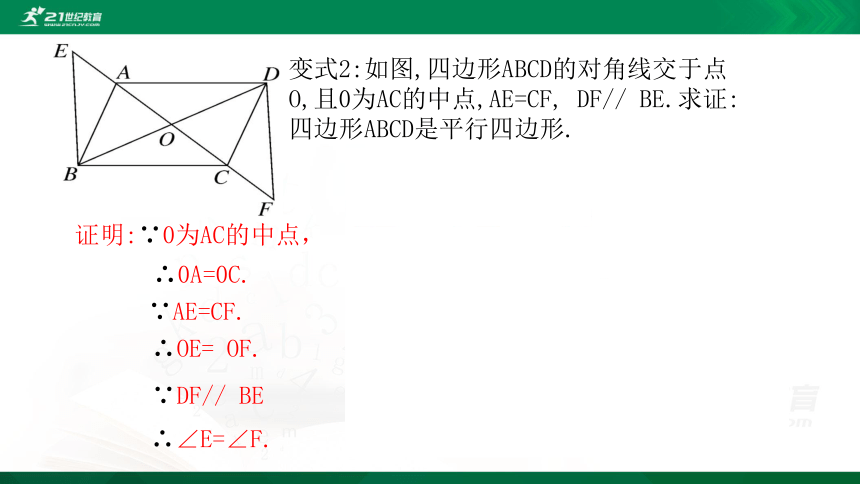
变式2:如图,四边形ABCD的对角线交于点O,且0为AC的中点,AE=CF, DF// BE.求证:四边形ABCD是平行四边形.
证明:∵0为AC的中点,
∴0A=0C.
∵AE=CF.
∴OE= OF.
∴∠E=∠F.
∵DF// BE
B
A
将线段AB沿着如图所给的方向和距离,
平移到 A′B′,构成四边形 A B B′A ′ 。
想一想:这个四边形具备了怎样的特征?
猜想:一组对边平行且相等的四边形是平行四边形.
你能用一句话概括你的发现吗?
新知探究
判定定理2:一组对边平行且相等的四边形是平行四边形.
′
已知:如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵ AB∥CD,
∴ ∠1=∠2.
∵AB=CD,AC=CA,
∴△ABC≌△CDA(SAS)..
∴四边形ABCD是平行四边形.
∴BC=DA.
B
D
C
A
1
2
你还有几种不同的证法
平行四边形的判定定理2:
一组对边平行且相等的四边形是平行四边形.
∵AB=CD,AB∥CD(已知)
∴四边形ABCD是平行四边形
B
C
A
D
平行四边形的判定定理3:
两组对角分别相等的四边形是平行四边形。
∵ ∠A=∠C,∠B=∠D (已知)
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形。)
B
D
A
C
已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °
证明:
即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)
同理可证AB∥CD
∴四边形ABCD是平行四边形
B
D
A
C
边:
定义1.两组对边分别平行的四边形是平行四边形
平行四边形的判定方法
判定定理1:两组对边相等的四边形是平行四边形
判定定理2:一组对边平行且相等的四边形是平行四边形.
本节小结:
平行四边形的判定定理3:
两组对角分别相等的四边形是平行四边形。
角:
1.在平行四边形ABCD中,AE⊥BC于E, AF⊥CD于F ,AE=4,AF=6,平行四边形ABCD的周长为 40 ,求平行四边形ABCD的面积.
A
B
C
D
E
F
4
6
x
20-x
4 x = 6 (20-x)
∴x=12
面积=12×4=48 或 8×6=48
作业
2.已知:如图,A′B′∥BA,B′C′∥CB,C′A′∥AC.
求证:(1) ∠ABC=∠B′, ∠CAB=∠A′,
∠BCA=∠C′;
(2) △ABC的顶点分别是△B′C′A′各边的中点.
A
C
B
A′
C′
B′
证明:(1) ∵ A′B′∥BA,C′B′∥BC,
∴ 四边形ABCB′是平行四边形.
∴ ∠ABC=∠B′(平行四边形的对角相等).
同理∠CAB=∠A′,∠BCA=∠C′.
(2) 由(1)证得四边形ABCB′是平行四边形.
同理,四边形ABA′C是平行四边形.
∴ AB=B′C, AB=A′C(平行四边形的对边相等).
∴ B′C=A′C.
同理 B′A=C′A, A′B=C′B.
∴ △ABC的顶点A、B、C分别是△B′C′A′的边B′C′、C′A′、A′B′的中点.
∴四边形EGFH为平行四边形
3.如图,在?ABCD中,E,F分别是AD,BC的中点,AF与EB相交于点G,CE与DF相交于点H,试说明四边形EGFH为平行四边形.
解:在平行四边形ABCD中,AD∥BC,AD=BC,
∵E,F分别为AD,BC的中点,
∴AE∥FC,AE=FC,ED∥BF,ED=BF,
∴四边形AFCE,EBFD都是平行四边形,
∴AF∥EC,BE∥FD,即GF∥EH,GE∥FH,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
八年级下
6.2平行四边形的判定第1课时
有两组对边分别平行的四边形
叫做
平行四边形
B
D
ABCD
A
C
B
D
A
C
O
平行四边形的性质:
边
平行四边形的对边平行
平行四边形的对边相等
角
平行四边形的对角相等
平行四边形的邻角互补
对角线
平行四边形的对角线互相平分
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
∴AB∥CD,AD∥BC
定义
∠A+∠B(∠D)=1800
∠A=∠C
∠B=∠D
∠C+∠B(∠D)=1800
AO=CO
BO=DO
判定定理1:两组对边相等的四边形是平行四边形
已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
B
C
A
D
证明:连结AC,
∵ AB=CD,AD=BC (已知)
又∵ AC=AC (公共边)
∴△ABC≌△CDA(SSS)
1
1
2
∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形
3
4
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。
∵AB=CD,AD=BC(已知)
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形。)
B
C
A
D
例1已知:平行四边形ABCD中,E.F分别是边AD BC的中点,求证:EB=DF
A
C
D
E
F
B
证明:∵四边形ABCD是平行四边形
∴AD∥BC AD=BC
∵ DE= AD BF= BC
∴DE∥BF DE=BF
∴四边形EBFD是平行四边形
∴EB=DF
变式:如图,已知AE⊥BD,CF⊥BD,E,F为垂足,AD// BC,DE=BF,求证:四边形AECF是平行四边形.
证明:∵AD//CB
∴∠B=∠D.
∴∠AED=∠CFB=90° ,AE//CF.
∵AE⊥BD,CF⊥BD
变式2:如图,四边形ABCD的对角线交于点O,且0为AC的中点,AE=CF, DF// BE.求证:四边形ABCD是平行四边形.
证明:∵0为AC的中点,
∴0A=0C.
∵AE=CF.
∴OE= OF.
∴∠E=∠F.
∵DF// BE
B
A
将线段AB沿着如图所给的方向和距离,
平移到 A′B′,构成四边形 A B B′A ′ 。
想一想:这个四边形具备了怎样的特征?
猜想:一组对边平行且相等的四边形是平行四边形.
你能用一句话概括你的发现吗?
新知探究
判定定理2:一组对边平行且相等的四边形是平行四边形.
′
已知:如图,在四边形ABCD中,AB∥CD,AB=CD.
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵ AB∥CD,
∴ ∠1=∠2.
∵AB=CD,AC=CA,
∴△ABC≌△CDA(SAS)..
∴四边形ABCD是平行四边形.
∴BC=DA.
B
D
C
A
1
2
你还有几种不同的证法
平行四边形的判定定理2:
一组对边平行且相等的四边形是平行四边形.
∵AB=CD,AB∥CD(已知)
∴四边形ABCD是平行四边形
B
C
A
D
平行四边形的判定定理3:
两组对角分别相等的四边形是平行四边形。
∵ ∠A=∠C,∠B=∠D (已知)
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形。)
B
D
A
C
已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °
证明:
即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)
同理可证AB∥CD
∴四边形ABCD是平行四边形
B
D
A
C
边:
定义1.两组对边分别平行的四边形是平行四边形
平行四边形的判定方法
判定定理1:两组对边相等的四边形是平行四边形
判定定理2:一组对边平行且相等的四边形是平行四边形.
本节小结:
平行四边形的判定定理3:
两组对角分别相等的四边形是平行四边形。
角:
1.在平行四边形ABCD中,AE⊥BC于E, AF⊥CD于F ,AE=4,AF=6,平行四边形ABCD的周长为 40 ,求平行四边形ABCD的面积.
A
B
C
D
E
F
4
6
x
20-x
4 x = 6 (20-x)
∴x=12
面积=12×4=48 或 8×6=48
作业
2.已知:如图,A′B′∥BA,B′C′∥CB,C′A′∥AC.
求证:(1) ∠ABC=∠B′, ∠CAB=∠A′,
∠BCA=∠C′;
(2) △ABC的顶点分别是△B′C′A′各边的中点.
A
C
B
A′
C′
B′
证明:(1) ∵ A′B′∥BA,C′B′∥BC,
∴ 四边形ABCB′是平行四边形.
∴ ∠ABC=∠B′(平行四边形的对角相等).
同理∠CAB=∠A′,∠BCA=∠C′.
(2) 由(1)证得四边形ABCB′是平行四边形.
同理,四边形ABA′C是平行四边形.
∴ AB=B′C, AB=A′C(平行四边形的对边相等).
∴ B′C=A′C.
同理 B′A=C′A, A′B=C′B.
∴ △ABC的顶点A、B、C分别是△B′C′A′的边B′C′、C′A′、A′B′的中点.
∴四边形EGFH为平行四边形
3.如图,在?ABCD中,E,F分别是AD,BC的中点,AF与EB相交于点G,CE与DF相交于点H,试说明四边形EGFH为平行四边形.
解:在平行四边形ABCD中,AD∥BC,AD=BC,
∵E,F分别为AD,BC的中点,
∴AE∥FC,AE=FC,ED∥BF,ED=BF,
∴四边形AFCE,EBFD都是平行四边形,
∴AF∥EC,BE∥FD,即GF∥EH,GE∥FH,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
