6.2.2 平行四边形的判定 课件(共20张PPT)
文档属性
| 名称 | 6.2.2 平行四边形的判定 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 00:00:00 | ||
图片预览



文档简介
数学北师大版
八年级下
6.2平行四边形的判定第2课时
如图,将两根细木条AC、BD的中心重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD,转动两根木条,它一直是一个平行四边形吗?你能证明吗?你又能得到什么结论?
判定定理4:对角线互相平分的四边形是平行四边形
几何语言:∵OA=OC,OB=OD
∴四边形ABCD是平行四边形
B
C
A
D
O
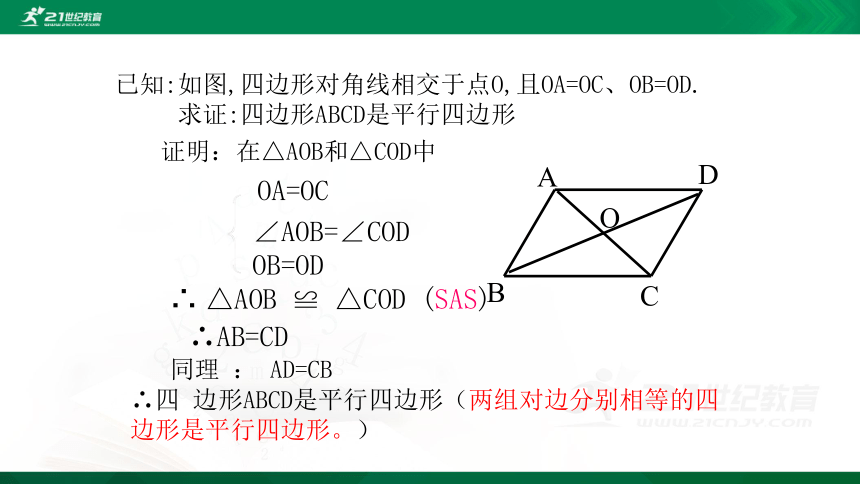
已知:如图,四边形对角线相交于点O,且OA=OC、OB=OD.
求证:四边形ABCD是平行四边形
证明:在△AOB和△COD中
∴ △AOB ≌ △COD (SAS)
∴AB=CD
同理 : AD=CB
∴四 边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。)
OA=OC
OB=OD
∠AOB=∠COD
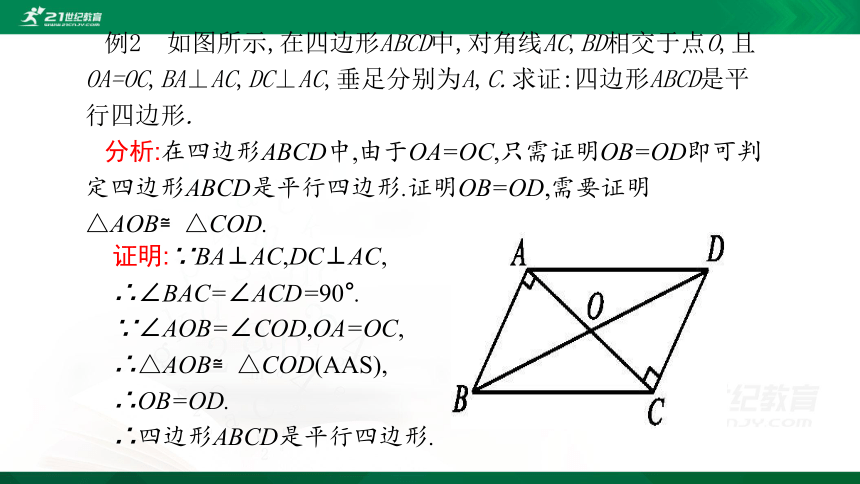
例2 如图所示,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,BA⊥AC,DC⊥AC,垂足分别为A,C.求证:四边形ABCD是平行四边形.
分析:在四边形ABCD中,由于OA=OC,只需证明OB=OD即可判定四边形ABCD是平行四边形.证明OB=OD,需要证明△AOB≌△COD.
证明:∵BA⊥AC,DC⊥AC,
∴∠BAC=∠ACD=90°.
∵∠AOB=∠COD,OA=OC,
∴△AOB≌△COD(AAS),
∴OB=OD.
∴四边形ABCD是平行四边形.
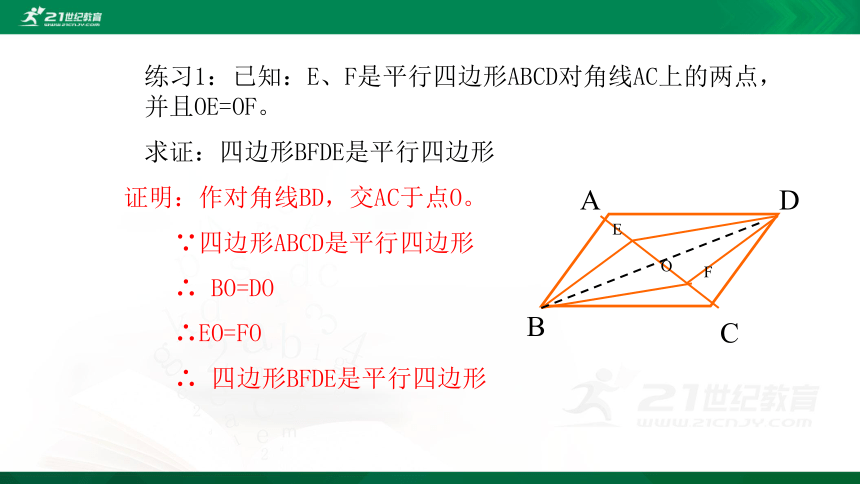
练习1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且OE=OF。
求证:四边形BFDE是平行四边形
证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ BO=DO
∴EO=FO
∴ 四边形BFDE是平行四边形
D
O
A
B
C
E
F
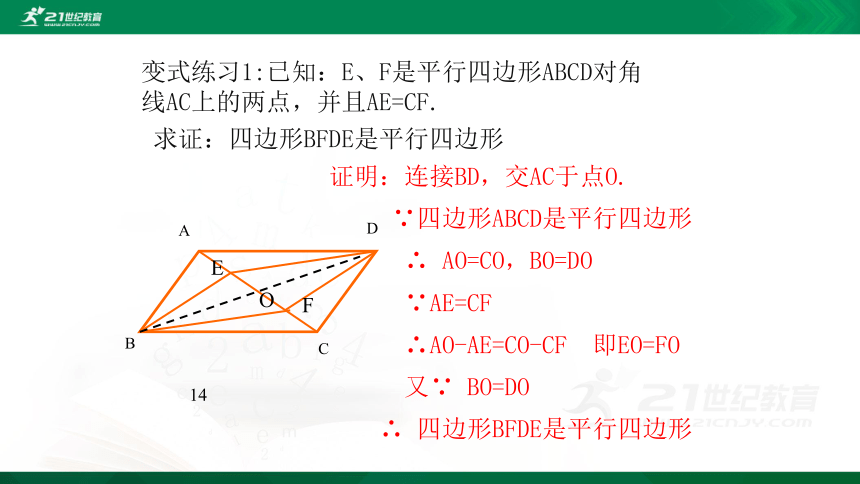
变式练习1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
D
O
A
B
C
E
F
证明:连接BD,交AC于点O.
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF 即EO=FO
又∵ BO=DO
∴ 四边形BFDE是平行四边形
求证:四边形BFDE是平行四边形
14
变式2 ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点。四边形EFGH是平行四边形吗?为什么?
O
G
E
F
D
H
C
B
A
答:四边形EFGH是平行四边形理由是:
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
又∵点E,F,G,H分别是OA,OB,OC,OD的中点
∴OE= OA,OG= OC,OF= OB,OH= OD
∴OE=OG,OF=OH
∴四边形EFGH是平行四边形
D
F
E
C
B
A
O
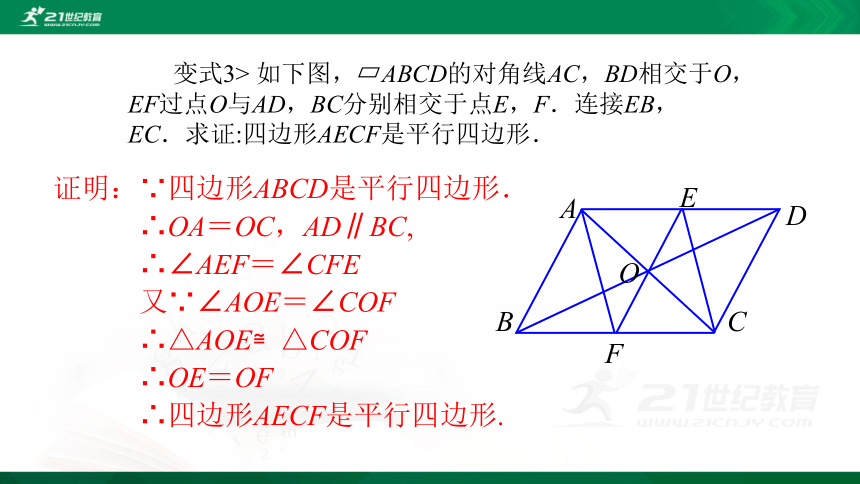
变式3> 如下图,?ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于点E,F.连接EB,EC.求证:四边形AECF是平行四边形.
证明:∵四边形ABCD是平行四边形.
∴OA=OC,AD∥BC,
∴∠AEF=∠CFE
又∵∠AOE=∠COF
∴△AOE≌△COF
∴OE=OF
∴四边形AECF是平行四边形.
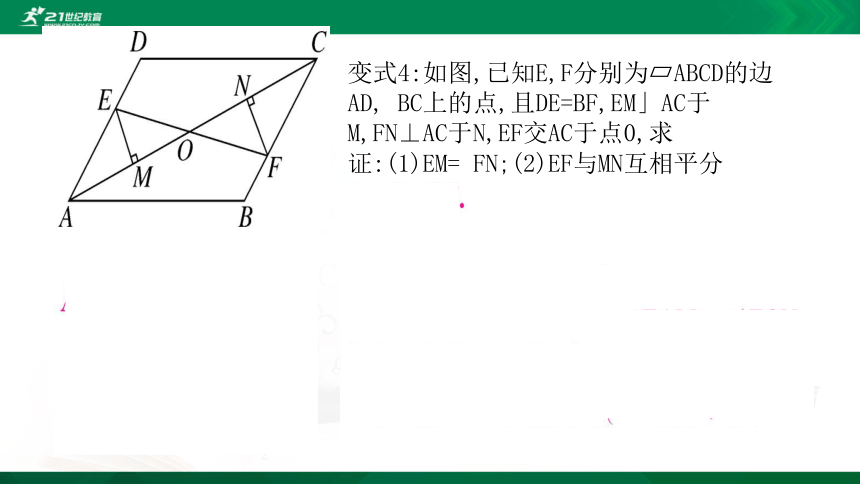
变式4:如图,已知E,F分别为?ABCD的边AD, BC上的点,且DE=BF,EM」AC于M,FN⊥AC于N,EF交AC于点0,求证:(1)EM= FN;(2)EF与MN互相平分
弯式4如图,已知E,F分别为?ABCD的边AD, BC上的点,
且DE=BF,EM」AC于M,FN⊥AC于N,EF交AC于点0,求证:(1)EM= FN;
(2)EF与MN互相平分
(1)根据定义:两组对边分别平行的四边
形叫做平行四边形。
(2)两组对边分别相等的四边形是平行
四边形。
(3)两组对角分别相等的四边形是平行四
边形。
(4)两条对角线互相平分的四边形是平
行四边形。
平行四边形的判定方法总结:
请你识别下列四边形哪些是平行四边形?请说明理由?
说一说
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
作业布置
1.已知:如图,在四边形ABCD中,M是边BC的中点,AM、BD互相平分于点0,求证:四边形AMCD是平行四边形.
2.如图,在△ABC中,∠ACB =90°,D是BC的中点,
DE⊥BC, CE// AD,月. AC =2,CE =4.(1 )求证:四边形ACED是平行四边形;(2)求四边形ACEB的周长.
(1)证明∵∠_ACB=90°,DE⊥BC
∴AC// DE,
又∵CE// AD,
∴四边形ACED是平行四边形
3.如图,?ABCD的边上依次有四点M、IN、K、L,且
AK= CM,BL= DN,请问∠NML等于∠NKL吗?为什么?.
4.如图,在平行四边形ABCD中,AC的平行线MN交DA的延长线于M,交DC的延长线于N,交AB ,BC于P,Q.(1 )请指出图中除?ABCD以外的平行四边形,并说明理由;(2)MP和QN能相等吗?若相等,请证明;若不相等,请说明理由.
解:(1)四边形AMQC和APNC是平行四边形,理由:
∵四边形ABCD是平行四边形,
∵MN// AC,MQ// AC,AM // QC, PN// AC,AP // CIN,
∴四边形AMQC,四边形APNC是平行四边形.
(2)MP=QN,理由如下:∵四边形AMQC是平行四边形,
∵四边形APNC是平行四边形,
∴MQ-PQ=PN-PQ,即MP = QN.
∴MD//BC, AB // ND,
∴MQ =AC,
∴PN=AC,
∴MQ=PN,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
八年级下
6.2平行四边形的判定第2课时
如图,将两根细木条AC、BD的中心重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD,转动两根木条,它一直是一个平行四边形吗?你能证明吗?你又能得到什么结论?
判定定理4:对角线互相平分的四边形是平行四边形
几何语言:∵OA=OC,OB=OD
∴四边形ABCD是平行四边形
B
C
A
D
O
已知:如图,四边形对角线相交于点O,且OA=OC、OB=OD.
求证:四边形ABCD是平行四边形
证明:在△AOB和△COD中
∴ △AOB ≌ △COD (SAS)
∴AB=CD
同理 : AD=CB
∴四 边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。)
OA=OC
OB=OD
∠AOB=∠COD
例2 如图所示,在四边形ABCD中,对角线AC,BD相交于点O,且OA=OC,BA⊥AC,DC⊥AC,垂足分别为A,C.求证:四边形ABCD是平行四边形.
分析:在四边形ABCD中,由于OA=OC,只需证明OB=OD即可判定四边形ABCD是平行四边形.证明OB=OD,需要证明△AOB≌△COD.
证明:∵BA⊥AC,DC⊥AC,
∴∠BAC=∠ACD=90°.
∵∠AOB=∠COD,OA=OC,
∴△AOB≌△COD(AAS),
∴OB=OD.
∴四边形ABCD是平行四边形.
练习1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且OE=OF。
求证:四边形BFDE是平行四边形
证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ BO=DO
∴EO=FO
∴ 四边形BFDE是平行四边形
D
O
A
B
C
E
F
变式练习1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
D
O
A
B
C
E
F
证明:连接BD,交AC于点O.
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF 即EO=FO
又∵ BO=DO
∴ 四边形BFDE是平行四边形
求证:四边形BFDE是平行四边形
14
变式2 ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点。四边形EFGH是平行四边形吗?为什么?
O
G
E
F
D
H
C
B
A
答:四边形EFGH是平行四边形理由是:
∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
又∵点E,F,G,H分别是OA,OB,OC,OD的中点
∴OE= OA,OG= OC,OF= OB,OH= OD
∴OE=OG,OF=OH
∴四边形EFGH是平行四边形
D
F
E
C
B
A
O
变式3> 如下图,?ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于点E,F.连接EB,EC.求证:四边形AECF是平行四边形.
证明:∵四边形ABCD是平行四边形.
∴OA=OC,AD∥BC,
∴∠AEF=∠CFE
又∵∠AOE=∠COF
∴△AOE≌△COF
∴OE=OF
∴四边形AECF是平行四边形.
变式4:如图,已知E,F分别为?ABCD的边AD, BC上的点,且DE=BF,EM」AC于M,FN⊥AC于N,EF交AC于点0,求证:(1)EM= FN;(2)EF与MN互相平分
弯式4如图,已知E,F分别为?ABCD的边AD, BC上的点,
且DE=BF,EM」AC于M,FN⊥AC于N,EF交AC于点0,求证:(1)EM= FN;
(2)EF与MN互相平分
(1)根据定义:两组对边分别平行的四边
形叫做平行四边形。
(2)两组对边分别相等的四边形是平行
四边形。
(3)两组对角分别相等的四边形是平行四
边形。
(4)两条对角线互相平分的四边形是平
行四边形。
平行四边形的判定方法总结:
请你识别下列四边形哪些是平行四边形?请说明理由?
说一说
A
D
C
B
110°
70°
110°
⑴
⑷
⑶
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
作业布置
1.已知:如图,在四边形ABCD中,M是边BC的中点,AM、BD互相平分于点0,求证:四边形AMCD是平行四边形.
2.如图,在△ABC中,∠ACB =90°,D是BC的中点,
DE⊥BC, CE// AD,月. AC =2,CE =4.(1 )求证:四边形ACED是平行四边形;(2)求四边形ACEB的周长.
(1)证明∵∠_ACB=90°,DE⊥BC
∴AC// DE,
又∵CE// AD,
∴四边形ACED是平行四边形
3.如图,?ABCD的边上依次有四点M、IN、K、L,且
AK= CM,BL= DN,请问∠NML等于∠NKL吗?为什么?.
4.如图,在平行四边形ABCD中,AC的平行线MN交DA的延长线于M,交DC的延长线于N,交AB ,BC于P,Q.(1 )请指出图中除?ABCD以外的平行四边形,并说明理由;(2)MP和QN能相等吗?若相等,请证明;若不相等,请说明理由.
解:(1)四边形AMQC和APNC是平行四边形,理由:
∵四边形ABCD是平行四边形,
∵MN// AC,MQ// AC,AM // QC, PN// AC,AP // CIN,
∴四边形AMQC,四边形APNC是平行四边形.
(2)MP=QN,理由如下:∵四边形AMQC是平行四边形,
∵四边形APNC是平行四边形,
∴MQ-PQ=PN-PQ,即MP = QN.
∴MD//BC, AB // ND,
∴MQ =AC,
∴PN=AC,
∴MQ=PN,
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
