6.2.3 平行四边形的判定 课件(共18张PPT)
文档属性
| 名称 | 6.2.3 平行四边形的判定 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 06:14:41 | ||
图片预览




文档简介
数学北师大版
八年级下
6.2平行四边形的判定第3课时
平行线之间的距离
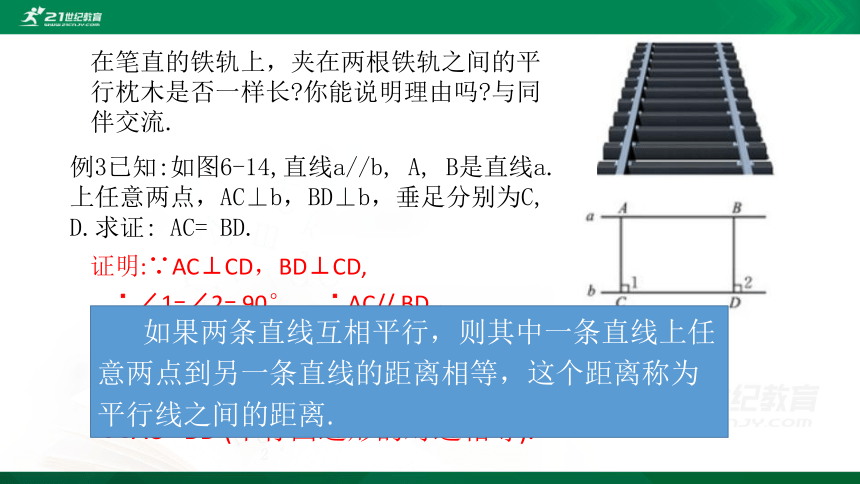
在笔直的铁轨上,夹在两根铁轨之间的平行枕木是否一样长?你能说明理由吗?与同伴交流.
例3已知:如图6-14,直线a//b, A, B是直线a.上任意两点,AC⊥b,BD⊥b,垂足分别为C, D.求证: AC= BD.
证明:∵AC⊥CD,BD⊥CD,
∴∠1=∠2= 90°.
∴AC// BD.,
∵AB// CD,
∴四边形ACDB是平行四边形(平行四边形的定义).
∴AC= BD (平行四边形的对边相等).
如果两条直线互相平行,则其中一条直线上任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离.
练习:如图,已知l1∥l2∥l3,相邻两条平行直线间的距离都等于1.若等腰直角三角形ABC的三个顶点分别在这三条平行直线上,求斜边AB的长.
分析:利用平行线间的距离相等构造全等三角形,然后利用勾股定理求AB的长.
解:如图,过点A作AD⊥l1于点D,过点B作BE⊥l1于点E.
∵∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE.
在△ACD和△CBE中,∠CAD=∠BCE,
∠ADC=∠BEC=90°,AC=BC,
∴△ACD≌△CBE(AAS).
∴CD=BE=1.
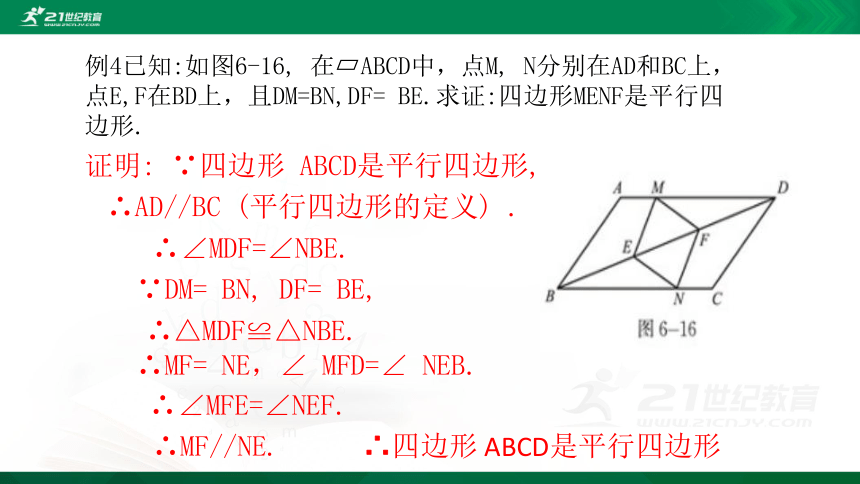
例4已知:如图6-16, 在?ABCD中,点M, N分别在AD和BC上,点E,F在BD上,且DM=BN,DF= BE.求证:四边形MENF是平行四边形.
证明: ∵四边形 ABCD是平行四边形,
∴AD//BC (平行四边形的定义) .
∴∠MDF=∠NBE.
∵DM= BN, DF= BE,
∴△MDF≌△NBE.
∴MF= NE,∠ MFD=∠ NEB.
∴∠MFE=∠NEF.
∴MF//NE.
∴四边形 ABCD是平行四边形
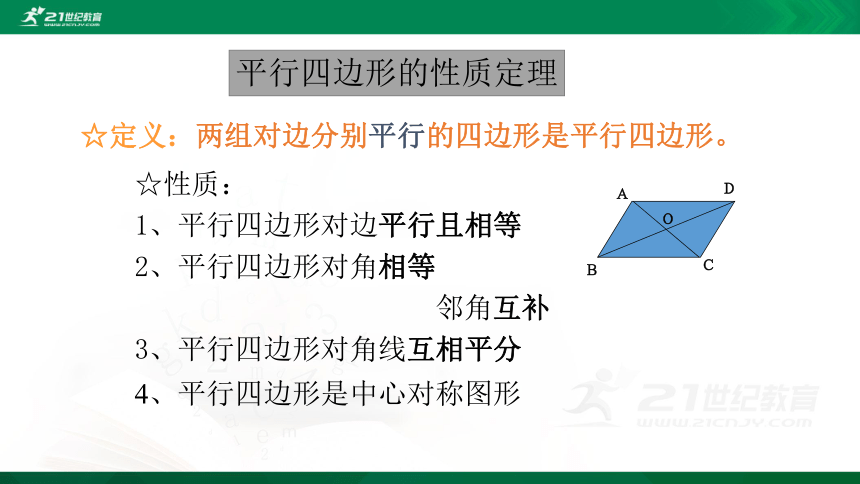
☆定义:两组对边分别平行的四边形是平行四边形。
☆性质:
1、平行四边形对边平行且相等
2、平行四边形对角相等
邻角互补
3、平行四边形对角线互相平分
4、平行四边形是中心对称图形
A
B
C
D
O
平行四边形的性质定理
边:
角
对角线
1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
4.两组对角分别相等的四边形是平行四边形
5.对角线互相平分的四边形是平行四边形
平行四边形的判定定理
例5.如图,已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
证明:四边形ABDF是平行四边形.
解:∵AF⊥AC,BD⊥AC,
∴AF∥BD,
∴∠DAF=∠ADE,
易知AD=CD,BD⊥AC,
∴∠CDB=∠ADE,
∴∠DAF=∠CDB,
又∠BCD=∠ADF,AD=DC,
∴△ADF≌△DCB,
∴AF=BD,
∴四边形ABDF是平行四边形
例6.如图,在?ABCD中,AD⊥BD,垂足为D,OA=4,OB=2,求:
(1)AD,AB的长及?ABCD的面积;
(2)平行线AB,DC之间的距离.
作业布置
1.如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,EF∥AC.
(1)求证:BE=AF;
(2)若∠ABC=60°,BD=6,求四边形ADEF的面积.
∴BE=AF
∴BE=DE,
∴∠DBE=∠BDE,
∴∠ABD=∠DBE,
∵BD是△ABC的角平分线,
∴AF=DE,
∴四边形ADEF是平行四边形,∠ABD=∠BDE,
解:(1)∵DE∥AB,EF∥AC,
(2)过点D作DG⊥AB于点G,过点E作EH⊥BD于点H,∵∠ABC=60°,BD是∠ABC的平分线,∴∠ABD=∠EBD=30°,
2.如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,EF∥AC.
(2)若∠ABC=60°,BD=6,求四边形ADEF的面积.
3.如图,在梯形ABCD中,AD∥BC,AD=24 cm,BC=30 cm,点P自点A向点D以1 cm/s的速度运动,到点D即停止,点Q自点C向点B以2 cm/s的速度运动,到点B即停止,直线PQ截梯形成两个四边形.问当P,Q同时出发,几秒后其中一个四边形为平行四边形?
解:设点P,Q同时出发t s后四边形PDCQ或四边形APQB是平行四边形,根据已知得到AP=t,PD=24-t,CQ=2t,BQ=30-2t.①若四边形PDCQ是平行四边形,则PD=CQ,∴24-t=2t,∴t=8,∴8 s后四边形PDCQ是平行四边形;②若四边形APQB是平行四边形,则AP=BQ,∴t=30-2t,∴t=10,∴10 s后四边形APQB是平行四边形
习题6.5
1.证明∵AB∥CD,
∴∠B+∠C=180°.
又∵∠B=∠D,∴∠D+∠C=180°.
∴AD∥BC.
∴四边形ABCD是平行四边形.
附习题答案
2.证明∵在?ABCD中,AD=BC,∠A=∠C,
又∵AE=CF,∴△ADE≌△CBF.∴DE=BF.
∵M,N分别是DE,BF的中点,
∴ME=FN.
∵AB∥CD,
∴∠CFB=∠ABF,
又∠AED=∠CFB,
∴∠AED=∠ABF.
∴DE∥BF,即ME∥FN.
∴四边形ENFM是平行四边形.
3.证明如图:连接EF,GH交于点O.
∵AE∥FC,AB∥DC,
∴四边形AFCE是平行四边形.
∴OF=OE.
∴∠FHO=∠EGO.
∴△FOH≌△EOG.∴OH=OG.
又∵OF=OE,
∴四边形FHEG是平行四边形.
∴EG=FH.
4.解因为两把曲尺已经平行,如果另一边缘对应曲尺上的刻度也相等,则满足一组对边平行且相等,故能得出木板的两边缘平行.
5.解如图这样的C点有5个,如图为C1,C2,C3,C4,C5.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
八年级下
6.2平行四边形的判定第3课时
平行线之间的距离
在笔直的铁轨上,夹在两根铁轨之间的平行枕木是否一样长?你能说明理由吗?与同伴交流.
例3已知:如图6-14,直线a//b, A, B是直线a.上任意两点,AC⊥b,BD⊥b,垂足分别为C, D.求证: AC= BD.
证明:∵AC⊥CD,BD⊥CD,
∴∠1=∠2= 90°.
∴AC// BD.,
∵AB// CD,
∴四边形ACDB是平行四边形(平行四边形的定义).
∴AC= BD (平行四边形的对边相等).
如果两条直线互相平行,则其中一条直线上任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离.
练习:如图,已知l1∥l2∥l3,相邻两条平行直线间的距离都等于1.若等腰直角三角形ABC的三个顶点分别在这三条平行直线上,求斜边AB的长.
分析:利用平行线间的距离相等构造全等三角形,然后利用勾股定理求AB的长.
解:如图,过点A作AD⊥l1于点D,过点B作BE⊥l1于点E.
∵∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,
∴∠CAD=∠BCE.
在△ACD和△CBE中,∠CAD=∠BCE,
∠ADC=∠BEC=90°,AC=BC,
∴△ACD≌△CBE(AAS).
∴CD=BE=1.
例4已知:如图6-16, 在?ABCD中,点M, N分别在AD和BC上,点E,F在BD上,且DM=BN,DF= BE.求证:四边形MENF是平行四边形.
证明: ∵四边形 ABCD是平行四边形,
∴AD//BC (平行四边形的定义) .
∴∠MDF=∠NBE.
∵DM= BN, DF= BE,
∴△MDF≌△NBE.
∴MF= NE,∠ MFD=∠ NEB.
∴∠MFE=∠NEF.
∴MF//NE.
∴四边形 ABCD是平行四边形
☆定义:两组对边分别平行的四边形是平行四边形。
☆性质:
1、平行四边形对边平行且相等
2、平行四边形对角相等
邻角互补
3、平行四边形对角线互相平分
4、平行四边形是中心对称图形
A
B
C
D
O
平行四边形的性质定理
边:
角
对角线
1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
4.两组对角分别相等的四边形是平行四边形
5.对角线互相平分的四边形是平行四边形
平行四边形的判定定理
例5.如图,已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC,
证明:四边形ABDF是平行四边形.
解:∵AF⊥AC,BD⊥AC,
∴AF∥BD,
∴∠DAF=∠ADE,
易知AD=CD,BD⊥AC,
∴∠CDB=∠ADE,
∴∠DAF=∠CDB,
又∠BCD=∠ADF,AD=DC,
∴△ADF≌△DCB,
∴AF=BD,
∴四边形ABDF是平行四边形
例6.如图,在?ABCD中,AD⊥BD,垂足为D,OA=4,OB=2,求:
(1)AD,AB的长及?ABCD的面积;
(2)平行线AB,DC之间的距离.
作业布置
1.如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,EF∥AC.
(1)求证:BE=AF;
(2)若∠ABC=60°,BD=6,求四边形ADEF的面积.
∴BE=AF
∴BE=DE,
∴∠DBE=∠BDE,
∴∠ABD=∠DBE,
∵BD是△ABC的角平分线,
∴AF=DE,
∴四边形ADEF是平行四边形,∠ABD=∠BDE,
解:(1)∵DE∥AB,EF∥AC,
(2)过点D作DG⊥AB于点G,过点E作EH⊥BD于点H,∵∠ABC=60°,BD是∠ABC的平分线,∴∠ABD=∠EBD=30°,
2.如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,EF∥AC.
(2)若∠ABC=60°,BD=6,求四边形ADEF的面积.
3.如图,在梯形ABCD中,AD∥BC,AD=24 cm,BC=30 cm,点P自点A向点D以1 cm/s的速度运动,到点D即停止,点Q自点C向点B以2 cm/s的速度运动,到点B即停止,直线PQ截梯形成两个四边形.问当P,Q同时出发,几秒后其中一个四边形为平行四边形?
解:设点P,Q同时出发t s后四边形PDCQ或四边形APQB是平行四边形,根据已知得到AP=t,PD=24-t,CQ=2t,BQ=30-2t.①若四边形PDCQ是平行四边形,则PD=CQ,∴24-t=2t,∴t=8,∴8 s后四边形PDCQ是平行四边形;②若四边形APQB是平行四边形,则AP=BQ,∴t=30-2t,∴t=10,∴10 s后四边形APQB是平行四边形
习题6.5
1.证明∵AB∥CD,
∴∠B+∠C=180°.
又∵∠B=∠D,∴∠D+∠C=180°.
∴AD∥BC.
∴四边形ABCD是平行四边形.
附习题答案
2.证明∵在?ABCD中,AD=BC,∠A=∠C,
又∵AE=CF,∴△ADE≌△CBF.∴DE=BF.
∵M,N分别是DE,BF的中点,
∴ME=FN.
∵AB∥CD,
∴∠CFB=∠ABF,
又∠AED=∠CFB,
∴∠AED=∠ABF.
∴DE∥BF,即ME∥FN.
∴四边形ENFM是平行四边形.
3.证明如图:连接EF,GH交于点O.
∵AE∥FC,AB∥DC,
∴四边形AFCE是平行四边形.
∴OF=OE.
∴∠FHO=∠EGO.
∴△FOH≌△EOG.∴OH=OG.
又∵OF=OE,
∴四边形FHEG是平行四边形.
∴EG=FH.
4.解因为两把曲尺已经平行,如果另一边缘对应曲尺上的刻度也相等,则满足一组对边平行且相等,故能得出木板的两边缘平行.
5.解如图这样的C点有5个,如图为C1,C2,C3,C4,C5.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
