6.3 三角形的中位线 课件(共35张PPT)
文档属性
| 名称 | 6.3 三角形的中位线 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 06:15:45 | ||
图片预览




文档简介
数学北师大版
八年级下
6.3三角形的中位线
A
B
C
D
E
F
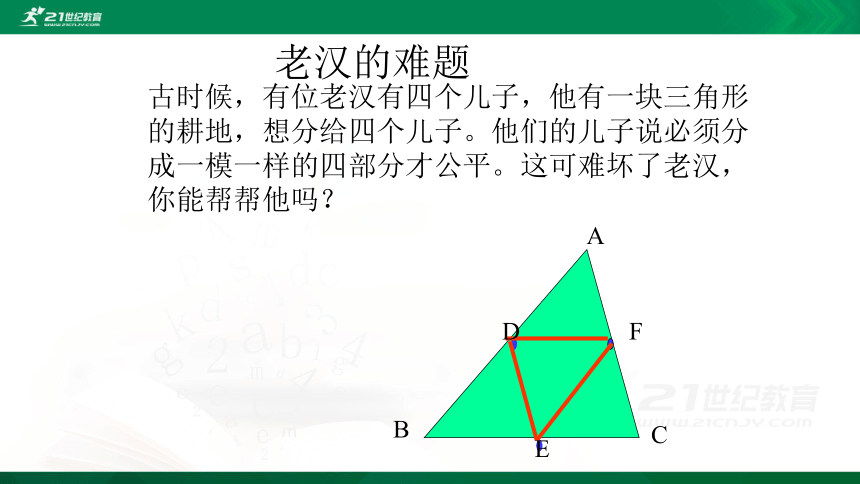
老汉的难题
古时候,有位老汉有四个儿子,他有一块三角形的耕地,想分给四个儿子。他们的儿子说必须分成一模一样的四部分才公平。这可难坏了老汉,你能帮帮他吗?
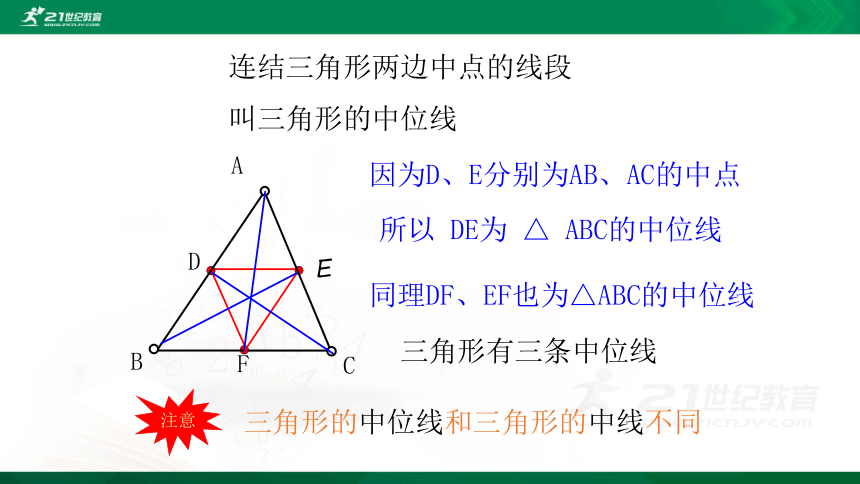
连结三角形两边中点的线段
叫三角形的中位线
三角形有三条中位线
因为D、E分别为AB、AC的中点
三角形的中位线和三角形的中线不同
同理DF、EF也为△ABC的中位线
E
D
F
A
C
B
所以 DE为 △ ABC的中位线
注意
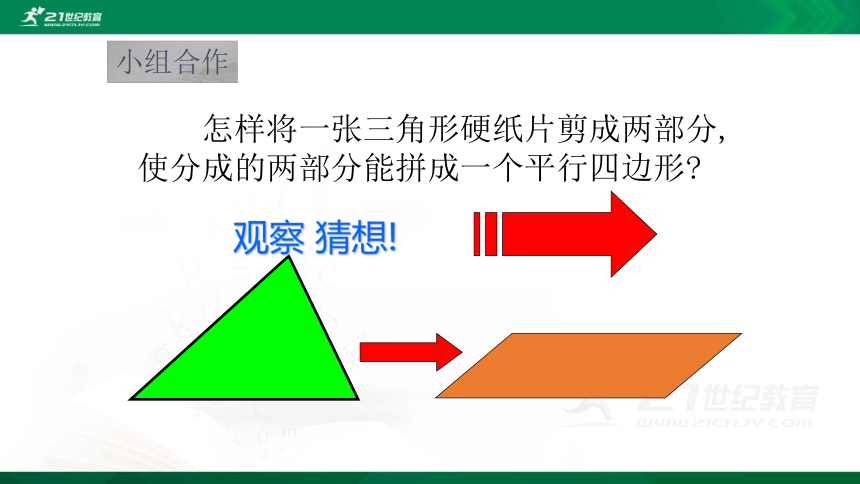
怎样将一张三角形硬纸片剪成两部分,使分成的两部分能拼成一个平行四边形?
观察 猜想!
小组合作
沿中位线剪开,再旋转.
沿中位线剪开,再旋转.
三角形的中位线平行于第三边,并且等于第三边的一半。
三角形中位线定理
A
B
C
D
E
F
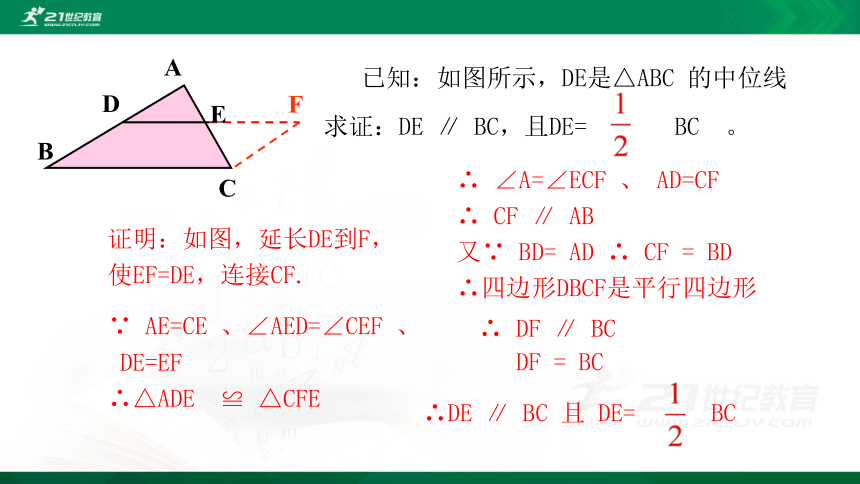
已知:如图所示,DE是△ABC 的中位线
求证:DE ∥ BC,且DE= BC 。
∵ AE=CE 、∠AED=∠CEF 、
DE=EF
∴△ADE ≌ △CFE
证明:如图,延长DE到F,
使EF=DE,连接CF.
∴ ∠A=∠ECF 、 AD=CF
∴ CF ∥ AB
又∵ BD= AD ∴ CF = BD
∴四边形DBCF是平行四边形
∴DE ∥ BC 且 DE= BC
∴ DF ∥ BC
DF = BC
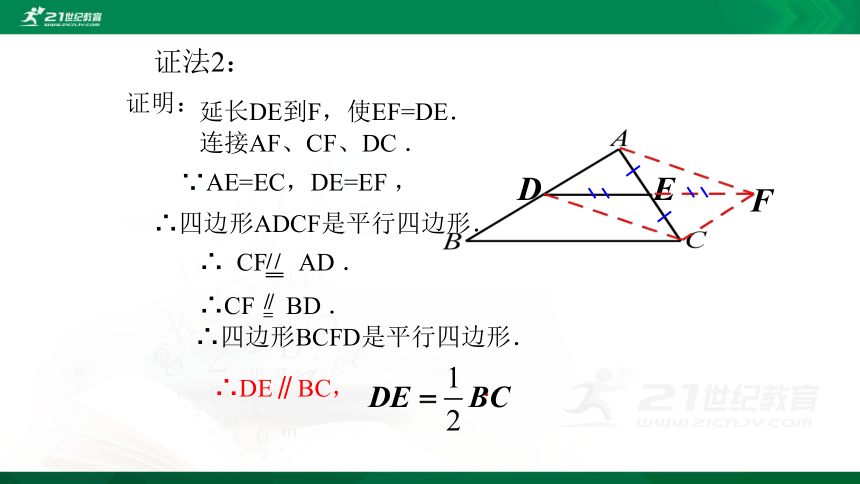
证明:
D
E
延长DE到F,使EF=DE.
连接AF、CF、DC .
∵AE=EC,DE=EF ,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形.
证法2:
∴ CF AD .
∴CF BD .
∴DE∥BC, .
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
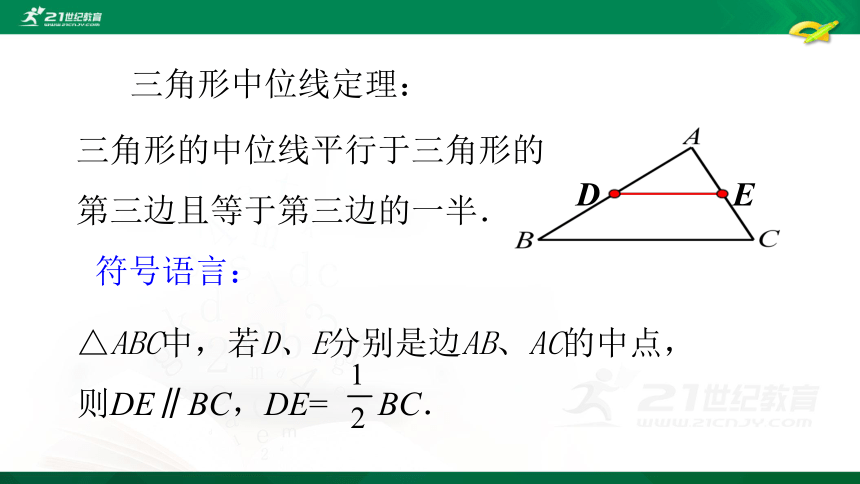
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.
三角形中位线定理:
符号语言:
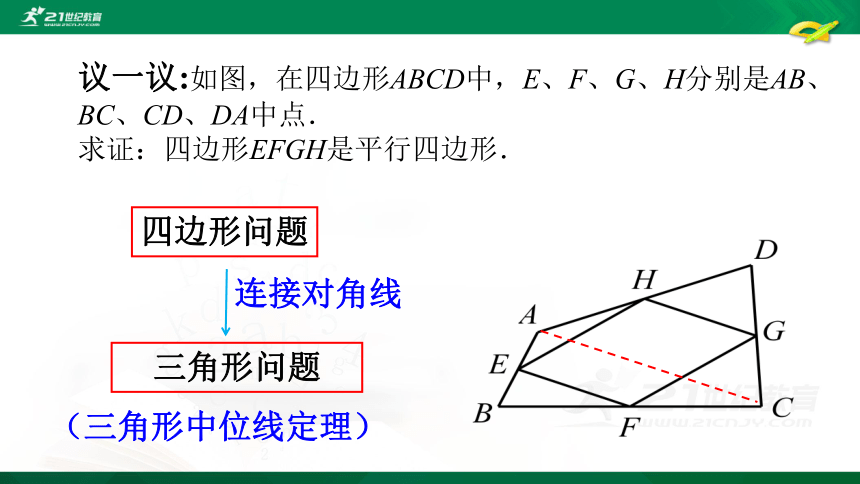
议一议:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.
四边形问题
连接对角线
三角形问题
(三角形中位线定理)
A
B
C
D
E
F
H
G
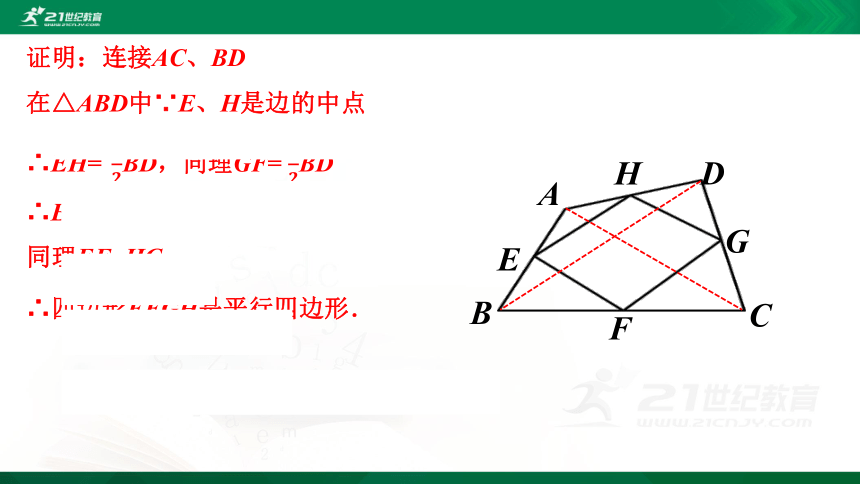
证明:连接AC、BD
在△ABD中∵E、H是边的中点
∴EH=?????????BD,同理GF= ????????BD
∴EH=GF
同理EF=HG
∴四边形EFGH是平行四边形.
?
2. 如图,A、B两点被池塘隔开,在AB外选一点
C,连接AC和BC,怎样量出A、B两点间的距离?
根据是什么?
分别画出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.
N
M
根据是三角形中位线定理.
随堂练习
例1.(10分)如图,已知E为?ABCD中DC边的延长线上的一点,且CE=DC,连接AE,交BC于点F,连接AC交BD于点O,连接OF,试说明AB=2OF.
例2.已知,如图6-3-10,在四边形ABCD中,AD=BC,P是对角线BD的中点,N是DC的中点,M是AB的中点,∠NPM=120°,求∠MNP的度数.
例3 求证三角形的一条中位线与第三边上的中线互相平分.
已知:如图所示,在△ABC中,AD=DB,BE=EC,AF=FC.
求证: AE、DF互相平分.
证明 连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分(平行四边形的对角线互相平分).
A
B
C
D
E
F
证:
∵ 点E,F分别为BC,AC的中点
∴ EF ∥AB,EF=1/2AB
∴ ∠DAC= ∠EFC=90 °
∵ AD=1/2AB, ∴ AD=EF,
∵ AF=CF,
∴ △ADF≌ △FEC (SAS)
∴ DF=EC ∵ BE=EC, ∴ DF=BE
例4:在△ABC中,∠BAC=90°,延长BA到点D,使AD=1/2AB,点E,F分别为BC,AC的中点,试说DF=BE理由
课后作业
1.如图,E是?ABCD的边DC的延长线上一点,且CE=DC,AE交BC于点F,AC交BD于点O,连接OF求证:AB= 20F
2.如图,AC,BD是四边形ABCD的对角线,E,F分别是AD,BC的中点,M,N分别是BD,AC的中点.求证:EF与MN互相平分.
3. 如图6-3-20,BM,CN分别平分△ABC的外角∠ABD,∠ACE,过点A分别作BM,CN的垂线,垂足分别为点M,N,交CB,BC的延长线于点D,E,连接MN.
求证:MN= (AB+BC+AC).
4. 如图6-3-21,已知△ABC是锐角三角形,分别以AB,AC为边向外侧作两个等边△ABM和△CAN. D,E,F分别是MB,BC,CN的中点,连接DE,FE,求证:DE=EF.
证明:如图转接BN,CM
备用习题
1.
2.
3.
4.如图,等边△ABC的边长是2,D,E分别为AB,AC的中点,延长BC至点F,使
解:(1)∵D,E分别为AB,AC的中点,
所以DE BC,∵CF= BC,
所以DE FC,即DE=CF
(2)∵DE FC,
∴四边形DEFC是平行四形,
∴DC= EF.
∵D为AB的中点,等边△ABC的边长是2,
∴ AD= BD= l,CD.⊥AB, BC= 2,∴DC= EF=
4. 如图,等边△ABC的边长是2,D,E分别为AB,AC的中点,延长BC至点F,使
5.如图,M是△ABC的边BC的中点,AN平分∠BAC,
BN⊥AN于点N,延长BN交AC于点D,已知AB=10,AC= 16.
(1)求证:BN= DN(2)求MN的长.;
5.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,AC= 16.
(1)求证:BN= DN(2)求MN的长.;
6.
7.如图,在△ABC中,AD为BC边上的中线,F为AC边上一点,AF= AC,BF交AD于点E,且E为AD的中点,EF=5 cm,求BF的长.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
八年级下
6.3三角形的中位线
A
B
C
D
E
F
老汉的难题
古时候,有位老汉有四个儿子,他有一块三角形的耕地,想分给四个儿子。他们的儿子说必须分成一模一样的四部分才公平。这可难坏了老汉,你能帮帮他吗?
连结三角形两边中点的线段
叫三角形的中位线
三角形有三条中位线
因为D、E分别为AB、AC的中点
三角形的中位线和三角形的中线不同
同理DF、EF也为△ABC的中位线
E
D
F
A
C
B
所以 DE为 △ ABC的中位线
注意
怎样将一张三角形硬纸片剪成两部分,使分成的两部分能拼成一个平行四边形?
观察 猜想!
小组合作
沿中位线剪开,再旋转.
沿中位线剪开,再旋转.
三角形的中位线平行于第三边,并且等于第三边的一半。
三角形中位线定理
A
B
C
D
E
F
已知:如图所示,DE是△ABC 的中位线
求证:DE ∥ BC,且DE= BC 。
∵ AE=CE 、∠AED=∠CEF 、
DE=EF
∴△ADE ≌ △CFE
证明:如图,延长DE到F,
使EF=DE,连接CF.
∴ ∠A=∠ECF 、 AD=CF
∴ CF ∥ AB
又∵ BD= AD ∴ CF = BD
∴四边形DBCF是平行四边形
∴DE ∥ BC 且 DE= BC
∴ DF ∥ BC
DF = BC
证明:
D
E
延长DE到F,使EF=DE.
连接AF、CF、DC .
∵AE=EC,DE=EF ,
∴四边形ADCF是平行四边形.
F
∴四边形BCFD是平行四边形.
证法2:
∴ CF AD .
∴CF BD .
∴DE∥BC, .
三角形的中位线平行于三角形的
第三边且等于第三边的一半.
D
E
△ABC中,若D、E分别是边AB、AC的中点,
则DE∥BC,DE= BC.
三角形中位线定理:
符号语言:
议一议:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA中点.
求证:四边形EFGH是平行四边形.
四边形问题
连接对角线
三角形问题
(三角形中位线定理)
A
B
C
D
E
F
H
G
证明:连接AC、BD
在△ABD中∵E、H是边的中点
∴EH=?????????BD,同理GF= ????????BD
∴EH=GF
同理EF=HG
∴四边形EFGH是平行四边形.
?
2. 如图,A、B两点被池塘隔开,在AB外选一点
C,连接AC和BC,怎样量出A、B两点间的距离?
根据是什么?
分别画出AC、BC中点M、N,
量出M、N两点间距离,则AB=2MN.
N
M
根据是三角形中位线定理.
随堂练习
例1.(10分)如图,已知E为?ABCD中DC边的延长线上的一点,且CE=DC,连接AE,交BC于点F,连接AC交BD于点O,连接OF,试说明AB=2OF.
例2.已知,如图6-3-10,在四边形ABCD中,AD=BC,P是对角线BD的中点,N是DC的中点,M是AB的中点,∠NPM=120°,求∠MNP的度数.
例3 求证三角形的一条中位线与第三边上的中线互相平分.
已知:如图所示,在△ABC中,AD=DB,BE=EC,AF=FC.
求证: AE、DF互相平分.
证明 连结DE、EF.
∵ AD=DB,BE=EC,
∴ DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分(平行四边形的对角线互相平分).
A
B
C
D
E
F
证:
∵ 点E,F分别为BC,AC的中点
∴ EF ∥AB,EF=1/2AB
∴ ∠DAC= ∠EFC=90 °
∵ AD=1/2AB, ∴ AD=EF,
∵ AF=CF,
∴ △ADF≌ △FEC (SAS)
∴ DF=EC ∵ BE=EC, ∴ DF=BE
例4:在△ABC中,∠BAC=90°,延长BA到点D,使AD=1/2AB,点E,F分别为BC,AC的中点,试说DF=BE理由
课后作业
1.如图,E是?ABCD的边DC的延长线上一点,且CE=DC,AE交BC于点F,AC交BD于点O,连接OF求证:AB= 20F
2.如图,AC,BD是四边形ABCD的对角线,E,F分别是AD,BC的中点,M,N分别是BD,AC的中点.求证:EF与MN互相平分.
3. 如图6-3-20,BM,CN分别平分△ABC的外角∠ABD,∠ACE,过点A分别作BM,CN的垂线,垂足分别为点M,N,交CB,BC的延长线于点D,E,连接MN.
求证:MN= (AB+BC+AC).
4. 如图6-3-21,已知△ABC是锐角三角形,分别以AB,AC为边向外侧作两个等边△ABM和△CAN. D,E,F分别是MB,BC,CN的中点,连接DE,FE,求证:DE=EF.
证明:如图转接BN,CM
备用习题
1.
2.
3.
4.如图,等边△ABC的边长是2,D,E分别为AB,AC的中点,延长BC至点F,使
解:(1)∵D,E分别为AB,AC的中点,
所以DE BC,∵CF= BC,
所以DE FC,即DE=CF
(2)∵DE FC,
∴四边形DEFC是平行四形,
∴DC= EF.
∵D为AB的中点,等边△ABC的边长是2,
∴ AD= BD= l,CD.⊥AB, BC= 2,∴DC= EF=
4. 如图,等边△ABC的边长是2,D,E分别为AB,AC的中点,延长BC至点F,使
5.如图,M是△ABC的边BC的中点,AN平分∠BAC,
BN⊥AN于点N,延长BN交AC于点D,已知AB=10,AC= 16.
(1)求证:BN= DN(2)求MN的长.;
5.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,AC= 16.
(1)求证:BN= DN(2)求MN的长.;
6.
7.如图,在△ABC中,AD为BC边上的中线,F为AC边上一点,AF= AC,BF交AD于点E,且E为AD的中点,EF=5 cm,求BF的长.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
