6.4.2 多边形的内角和与外角和 课件(共20张PPT)
文档属性
| 名称 | 6.4.2 多边形的内角和与外角和 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 06:18:08 | ||
图片预览




文档简介
数学北师大版
八年级下
6.4 多边形的内角和与外角和第2课时
与外角和
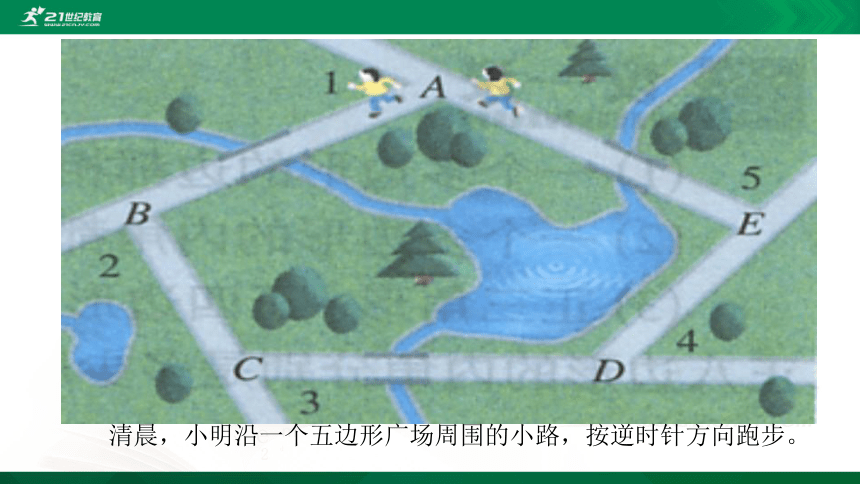
清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出?1+ ? 2+ ? 3+ ? 4+ ? 5的结果吗?你是怎样得到的?
问题
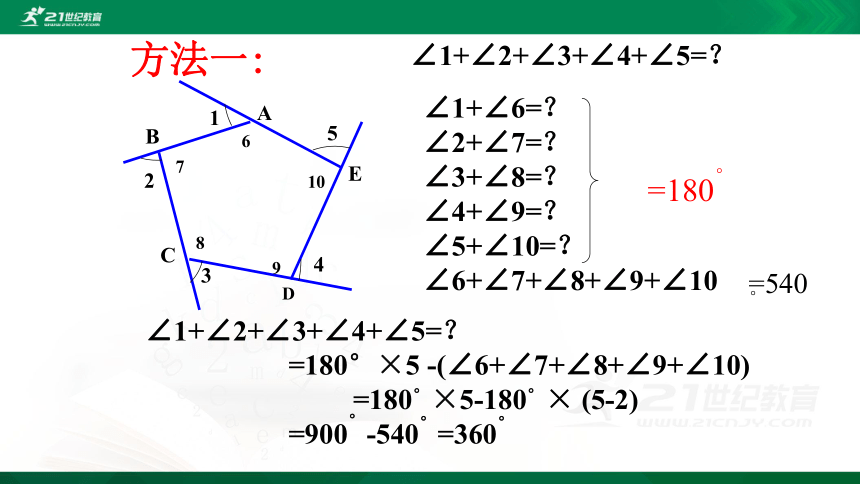
方法一:
A
B
C
D
E
1
2
3
4
5
6
7
8
9
10
∠1+∠6=?
∠2+∠7=?
∠3+∠8=?
∠4+∠9=?
∠5+∠10=?
∠6+∠7+∠8+∠9+∠10
∠1+∠2+∠3+∠4+∠5=?
=180°×5 -(∠6+∠7+∠8+∠9+∠10) =180°×5-180°× (5-2)
=900°-540°=360°
=180°
∠1+∠2+∠3+∠4+∠5=?
=540°
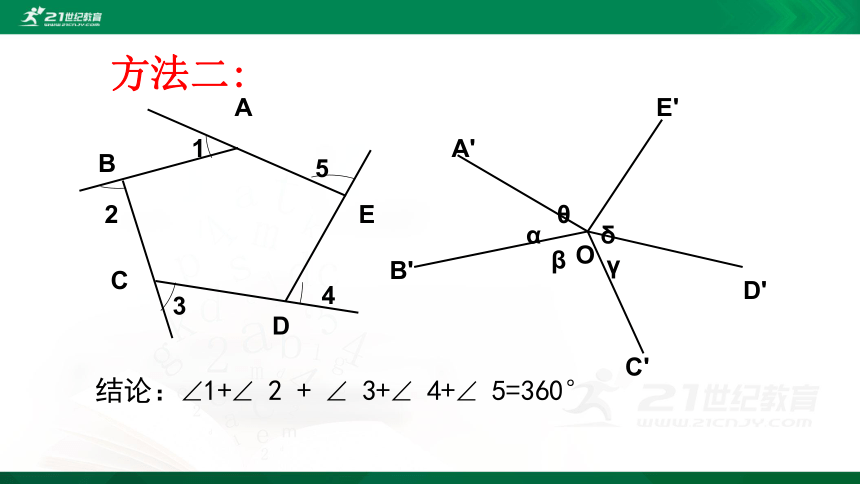
结论:?1+? 2 + ? 3+? 4+? 5=360°
C'
A
B
C
D
E
A'
D'
E'
B'
O
β
γ
δ
θ
α
1
2
3
4
5
方法二:
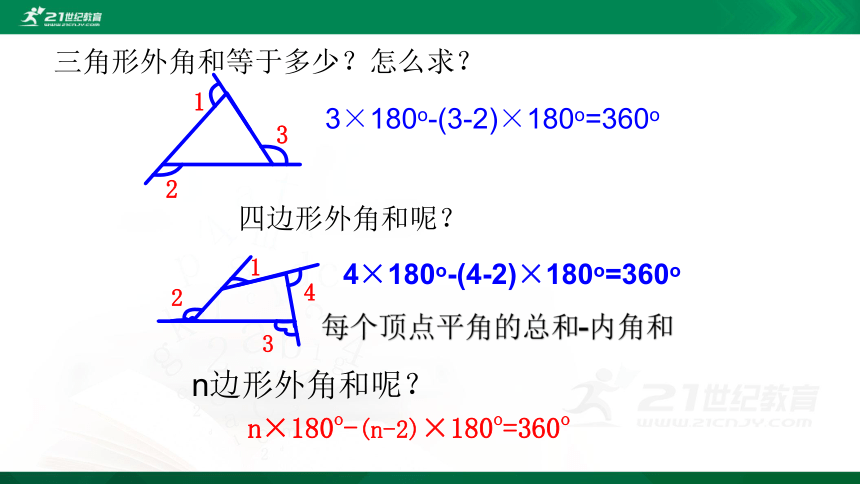
三角形外角和等于多少?怎么求?
3×180o-(3-2)×180o=360o
4×180o-(4-2)×180o=360o
四边形外角和呢?
n边形外角和呢?
n×180o-(n-2)×180o=360o
每个顶点平角的总和-内角和
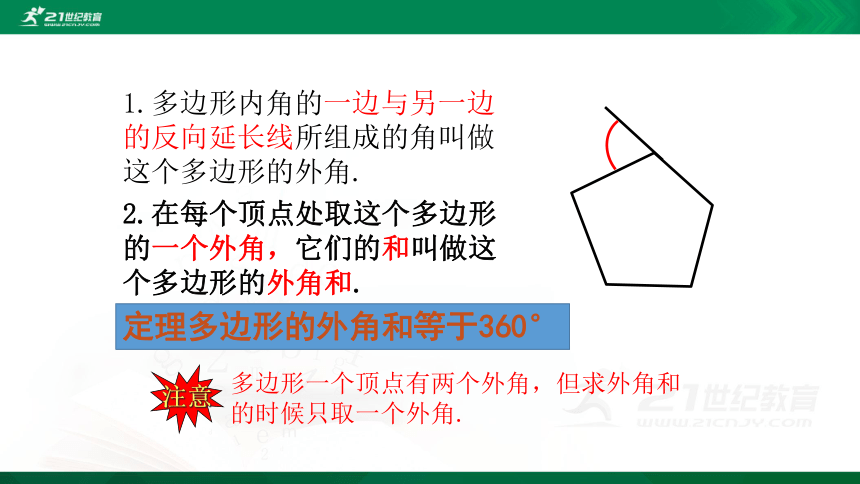
1.多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
2.在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
多边形一个顶点有两个外角,但求外角和的时候只取一个外角.
注意
定理多边形的外角和等于360°
解: 设这个多边形的边数为n,
则它的内角和等于 (n-2) ×180°,
外角和等于360?,所以
(n-2) ×180= 3×360
n = 8
?这个多边形的边数为8.
例2.一个多边形的内角和等于它的外角和的3倍,它是几边形?
课堂练习
1.若一个多边形的每一个外角都等于15°,则这个多边形的边数是________
2.若一个十边形的每个外角都相等,则它的每个外角的度数为________度,每个内角的度数为________度.
3.若一个多边形的内角和等于它的外角和,
则它的边数是_______.
4.多边形的边数增加1,则内角和增加
_____度.外角和增加_____度
24
36
144
4
180
0
例:一个正多边形的一个内角为150°,它是几边形?
解法一:依题意可得
(n-2)·180°=n·150
解得n=12
答:它是十二边形。
解法二:依题意可得它的每一个外角180°-150°=30°
n=360°÷30°=12
解:设这个多边形的边数为n,除去的这个角为x°.
依题意,得(n-2)·180°=2210°+x°.
即(n-2)·180°=12×180°+(50°+x°),
∵等式右边是180°的整数倍.
∵0°<x°<180°,∴x°=130°,此时n=15.
∴这个多边形是十五边形,除去的这个角等于130°.
练习1若一个多边形除去一个内角后,其余各内角的和为2210°,则这个多边形是几边形?除去的这个角等于多少度?
2、n边形的内角和等于多少?
n边形的内角和等于(n - 2)?180°
1、过n边形的某一个顶点的对角线有几条?
这些对角线把多边形分成几个三角形?
有(n - 3) 条。
被分成(n - 2) 个三角形。
3、n边形的外角和是3600,与多边形的边数无关.
本节课小结
1.(1)如图,小陈从点O出发,前进5m后向右转20°,再前进5m后又向右转20°,…,这样一直走下去,他第一次回到出发点O时,一共走了( )
A.60m B.100m C.90m D.120m
解析:小陈的行走路线围成的图形是一个正多边形,它的每条边长都是5m,每个外角都是20°,所以围成的正多边形的边数是360°÷20°=18,故小陈行走的总路程为5×18=90(m).
C
课后作业
(2).如图,在△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2等于( )
B
C
A
1
2
第5题
A.360° B.250° C.180° D.140°
B
(3))如图6-4 -4,正五边形ABCDE中,对角线AC与BE相交于点F,则∠AFE=( )度.
2.有一个正多边形,它的一个外角等于相邻内角的0.2倍,这个多边形是几边形?
解析:根据外角与其相邻内角互补及已知条件,可以求得它的每一个外角都为30°,每一个内角都为150°,再利用外角相等及外角和为360°可求得边数,进而可确定是几边形.
解:设这个正多边形的每个内角为x°,
则每个外角为0.2x°,
得x°+0.2x°=180°,
解得x°=150°,
则0.2x°=0.2×150°=30°.
这个正多边形的边数为:360°÷30°=12.
因此,这个多边形是十二边形.
3.在四边形ABCD中,∠A,∠B,∠C,∠D的外角的度数的比为4 :7 : 5 : 8,求四边形各内角的度数.
4.(1)请你根据已经学过的知识求出下面星形图①中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图①中星形截去一个角,如图②,请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
解:(1)∵∠1=∠2+∠D=∠B+∠E+∠D,
∠1+∠A+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
(2)∵∠1=∠2+∠F=∠B+∠E+∠F,
∠1+∠A+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
(3)若再对图②中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图③中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?(只要写出结论,不需要写出解题过程)
(3)根据图中可得出规律
∠A+∠B+∠C+∠D+∠E=180°,每截去一个角则会增加180°,
∴当截去5个角时增加了180°×5,
则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=1 080°.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
八年级下
6.4 多边形的内角和与外角和第2课时
与外角和
清晨,小明沿一个五边形广场周围的小路,按逆时针方向跑步。
(1)小明每从一条街道转到下一条街道时,身体转过的角是哪个角?
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)在上图中,你能求出?1+ ? 2+ ? 3+ ? 4+ ? 5的结果吗?你是怎样得到的?
问题
方法一:
A
B
C
D
E
1
2
3
4
5
6
7
8
9
10
∠1+∠6=?
∠2+∠7=?
∠3+∠8=?
∠4+∠9=?
∠5+∠10=?
∠6+∠7+∠8+∠9+∠10
∠1+∠2+∠3+∠4+∠5=?
=180°×5 -(∠6+∠7+∠8+∠9+∠10) =180°×5-180°× (5-2)
=900°-540°=360°
=180°
∠1+∠2+∠3+∠4+∠5=?
=540°
结论:?1+? 2 + ? 3+? 4+? 5=360°
C'
A
B
C
D
E
A'
D'
E'
B'
O
β
γ
δ
θ
α
1
2
3
4
5
方法二:
三角形外角和等于多少?怎么求?
3×180o-(3-2)×180o=360o
4×180o-(4-2)×180o=360o
四边形外角和呢?
n边形外角和呢?
n×180o-(n-2)×180o=360o
每个顶点平角的总和-内角和
1.多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
2.在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
多边形一个顶点有两个外角,但求外角和的时候只取一个外角.
注意
定理多边形的外角和等于360°
解: 设这个多边形的边数为n,
则它的内角和等于 (n-2) ×180°,
外角和等于360?,所以
(n-2) ×180= 3×360
n = 8
?这个多边形的边数为8.
例2.一个多边形的内角和等于它的外角和的3倍,它是几边形?
课堂练习
1.若一个多边形的每一个外角都等于15°,则这个多边形的边数是________
2.若一个十边形的每个外角都相等,则它的每个外角的度数为________度,每个内角的度数为________度.
3.若一个多边形的内角和等于它的外角和,
则它的边数是_______.
4.多边形的边数增加1,则内角和增加
_____度.外角和增加_____度
24
36
144
4
180
0
例:一个正多边形的一个内角为150°,它是几边形?
解法一:依题意可得
(n-2)·180°=n·150
解得n=12
答:它是十二边形。
解法二:依题意可得它的每一个外角180°-150°=30°
n=360°÷30°=12
解:设这个多边形的边数为n,除去的这个角为x°.
依题意,得(n-2)·180°=2210°+x°.
即(n-2)·180°=12×180°+(50°+x°),
∵等式右边是180°的整数倍.
∵0°<x°<180°,∴x°=130°,此时n=15.
∴这个多边形是十五边形,除去的这个角等于130°.
练习1若一个多边形除去一个内角后,其余各内角的和为2210°,则这个多边形是几边形?除去的这个角等于多少度?
2、n边形的内角和等于多少?
n边形的内角和等于(n - 2)?180°
1、过n边形的某一个顶点的对角线有几条?
这些对角线把多边形分成几个三角形?
有(n - 3) 条。
被分成(n - 2) 个三角形。
3、n边形的外角和是3600,与多边形的边数无关.
本节课小结
1.(1)如图,小陈从点O出发,前进5m后向右转20°,再前进5m后又向右转20°,…,这样一直走下去,他第一次回到出发点O时,一共走了( )
A.60m B.100m C.90m D.120m
解析:小陈的行走路线围成的图形是一个正多边形,它的每条边长都是5m,每个外角都是20°,所以围成的正多边形的边数是360°÷20°=18,故小陈行走的总路程为5×18=90(m).
C
课后作业
(2).如图,在△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2等于( )
B
C
A
1
2
第5题
A.360° B.250° C.180° D.140°
B
(3))如图6-4 -4,正五边形ABCDE中,对角线AC与BE相交于点F,则∠AFE=( )度.
2.有一个正多边形,它的一个外角等于相邻内角的0.2倍,这个多边形是几边形?
解析:根据外角与其相邻内角互补及已知条件,可以求得它的每一个外角都为30°,每一个内角都为150°,再利用外角相等及外角和为360°可求得边数,进而可确定是几边形.
解:设这个正多边形的每个内角为x°,
则每个外角为0.2x°,
得x°+0.2x°=180°,
解得x°=150°,
则0.2x°=0.2×150°=30°.
这个正多边形的边数为:360°÷30°=12.
因此,这个多边形是十二边形.
3.在四边形ABCD中,∠A,∠B,∠C,∠D的外角的度数的比为4 :7 : 5 : 8,求四边形各内角的度数.
4.(1)请你根据已经学过的知识求出下面星形图①中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图①中星形截去一个角,如图②,请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
解:(1)∵∠1=∠2+∠D=∠B+∠E+∠D,
∠1+∠A+∠C=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
(2)∵∠1=∠2+∠F=∠B+∠E+∠F,
∠1+∠A+∠C+∠D=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
(3)若再对图②中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图③中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?(只要写出结论,不需要写出解题过程)
(3)根据图中可得出规律
∠A+∠B+∠C+∠D+∠E=180°,每截去一个角则会增加180°,
∴当截去5个角时增加了180°×5,
则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=1 080°.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
