1.4 角平分线第2课时三角形的内角平分线 课件(共20张PPT)
文档属性
| 名称 | 1.4 角平分线第2课时三角形的内角平分线 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 16:26:37 | ||
图片预览


文档简介
数学北师大版
八年级下
1.4 角平分线第2课时三角形的内角平分线
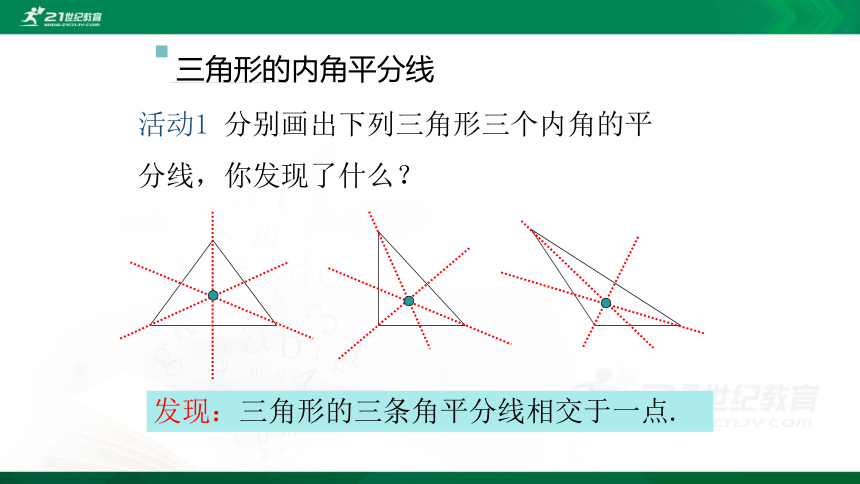
活动1 分别画出下列三角形三个内角的平分线,你发现了什么?
三角形的内角平分线
发现:三角形的三条角平分线相交于一点.
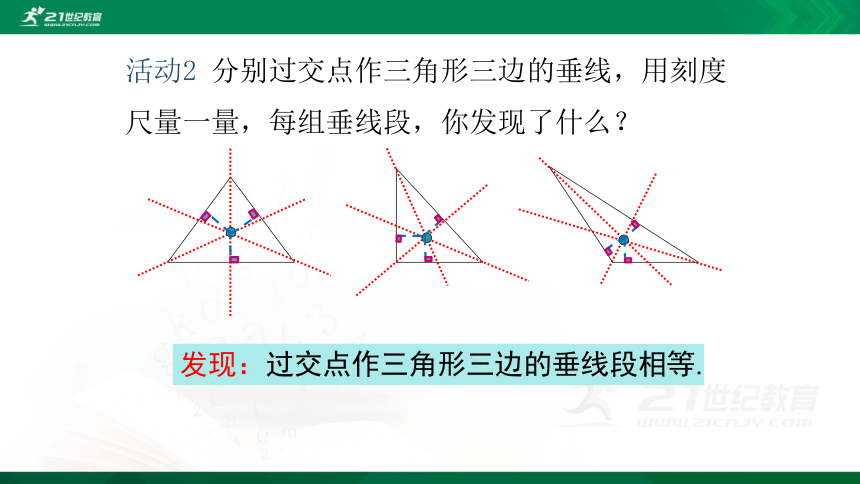
活动2 分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的垂线段相等.
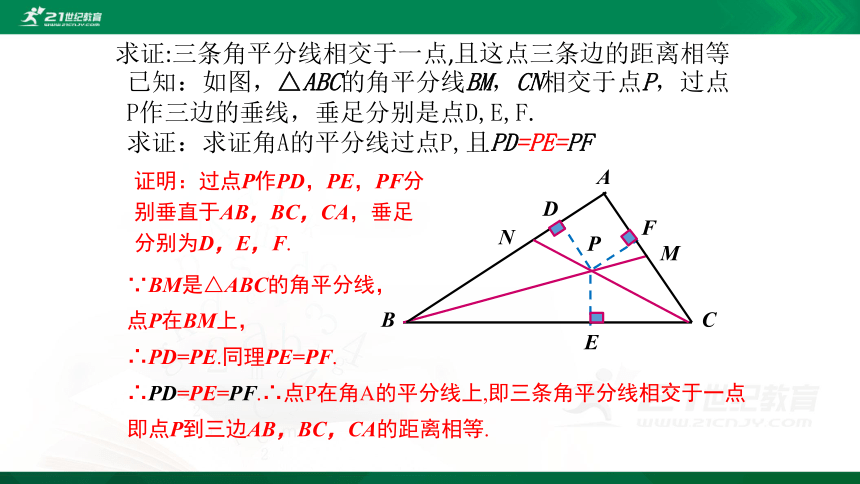
已知:如图,△ABC的角平分线BM,CN相交于点P,过点P作三边的垂线,垂足分别是点D,E,F.
求证:求证角A的平分线过点P,且PD=PE=PF
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
点P在BM上,
∴PD=PE.同理PE=PF.
∴PD=PE=PF.∴点P在角A的平分线上,即三条角平分线相交于一点
即点P到三边AB,BC,CA的距离相等.
D
E
F
A
B
C
P
N
M
求证:三条角平分线相交于一点,且这点三条边的距离相等
P1
P2
P3
P4
l1
l2
l3
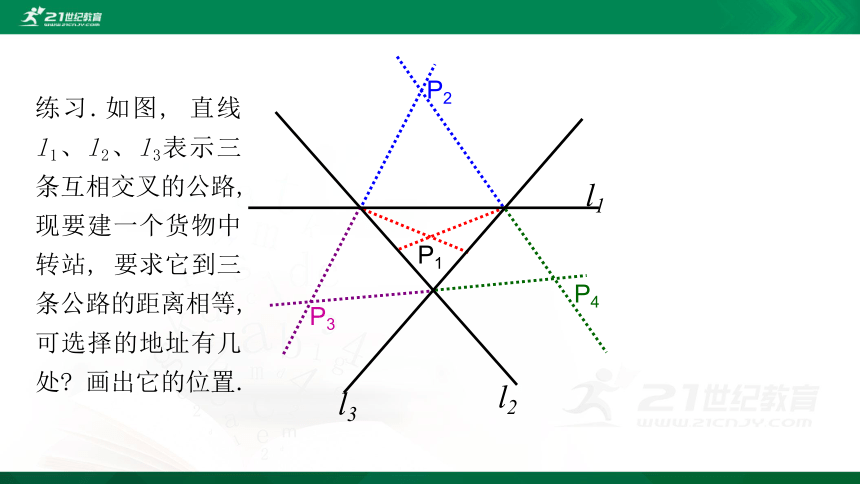
练习.如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站, 要求它到三条公路的距离相等, 可选择的地址有几处? 画出它的位置.
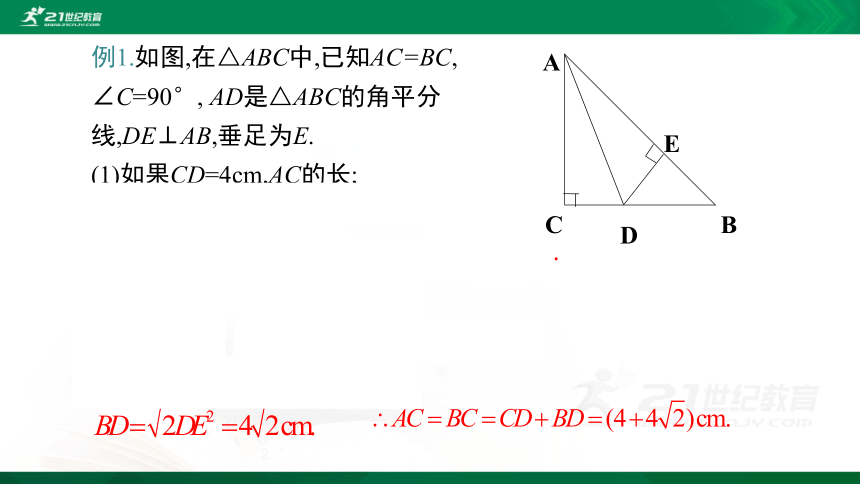
例1.如图,在△ABC中,已知AC=BC, ∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)如果CD=4cm,AC的长;
E
D
A
B
C
(1)解:∵AD是△ABC的角平分线,DE⊥AB,垂足为E,∴DE=CD=4cm.
∵AC=BC,∴∠B=∠BAC.
∵∠C=90°,∴∠B=45°.∴BE=DE.
在等腰直角三角形BDE中,
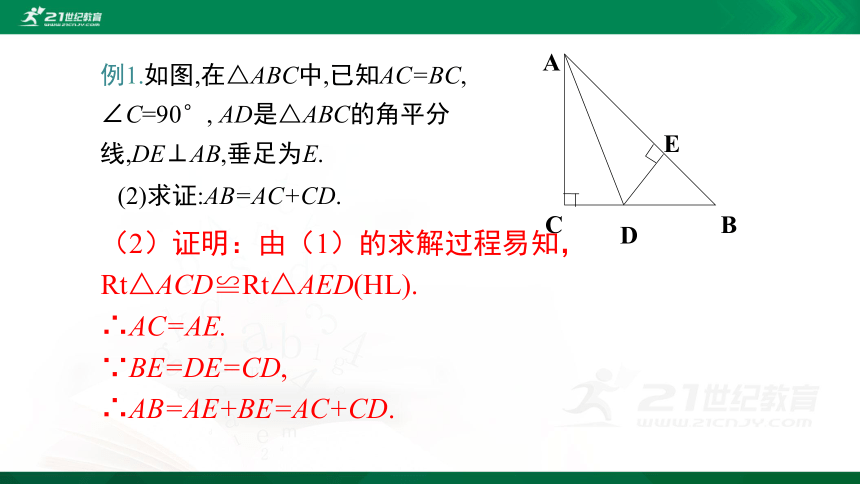
(2)求证:AB=AC+CD.
E
D
A
B
C
(2)证明:由(1)的求解过程易知,
Rt△ACD≌Rt△AED(HL).
∴AC=AE.
∵BE=DE=CD,
∴AB=AE+BE=AC+CD.
例1.如图,在△ABC中,已知AC=BC, ∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
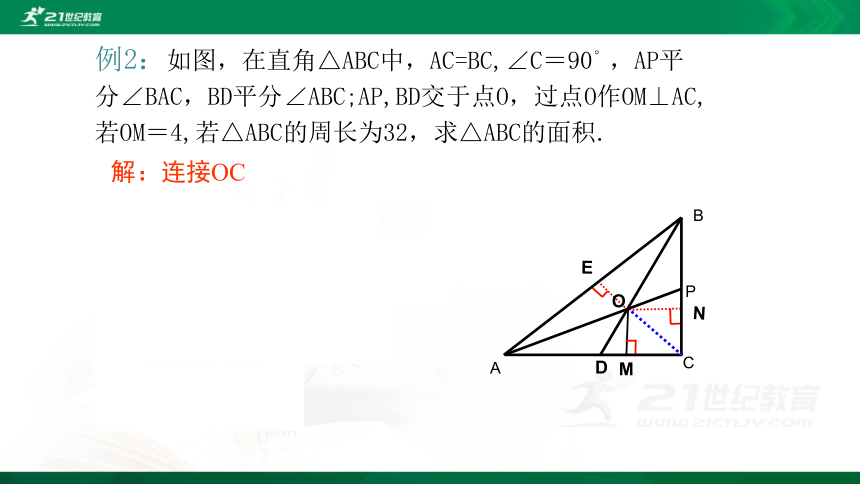
解:连接OC
M
E
N
A
B
C
P
O
D
例2:如图,在直角△ABC中,AC=BC,∠C=90°,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4,若△ABC的周长为32,求△ABC的面积.
解:点P在∠AOB的平分线上.
理由如下:过点P分别作PD⊥OA于点D,PE⊥OB于点E.
∵S四边形OMPG=S四边形OFPN,
∴S四边形OMPG-S四边形OMPF=S四边形OFPN-S四边形OMPF,
即S△FPG=S△MPN.
∵FG=MN,∴PD=PE.
又PD⊥OA,PE⊥OB,
∴点P在∠AOB的平分线上.
例3 如图,点F,G是OA上的两点,点M,N是OB上的两点,且FG=MN,四边形OMPG的面积与四边形OFPN的面积相等.那么点P是否在∠AOB的平分线上?请说明理由.
习题1.10
1.证明∵∠C=90°,∠B=30°,
∴∠BAC=60°.
∵AD平分∠BAC,
∴∠DAC=∠BAD=30°.
∵∠B=30°,
∴∠BAD=∠B=30°.
∴BD=AD.
∵∠C=90°,∠DAC=30°,
∴AD=2CD.∴BD=2CD.
2.证明如图所示,过点F作FG⊥AD,FH⊥AE,FI⊥BC.
∵BF是∠DBC的平分线,∴FG=FI.
同理,FH=FI.∴FG=FH.
∴点F在∠DAE的平分线上.
3.证明(1)∵P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB,∴PC=PD.
又∵OP=OP,∴Rt△OCP≌Rt△ODP.
∴OC=OD.
(2)∵OC=OD,∠COP=∠DOP,
∴OP是CD的垂直平分线.
4.解(1)如图,作∠BAC的角平分线AF或作∠BAC的外角∠CAE的外角平分线AN,则直线AF或直线AN上任意一点(A除外)都满足到AB,AC的距离相等,可以修建油库.
(2)如图,作∠BAC的角平分线,作∠BCA的角平分线,两角平分线交于一点P,P点是修建油库的位置.
1.三角形三条角平分线的性质定理:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.?
2.三角形三个内角平分线的交点只有一个,实际作图时,只需作出两个角的平分线,第三个角的平分线必过这两条角平分线的交点.
3.利用面积法求距离的方法:三角形角平分线交点与三个顶点的连线,把原三角形分割成了三个小三角形,利用小三角形的面积之和等于原三角形的面积,是求角平分线交点到三边距离的常用方法.
归纳总结
1.如图,在△ABC中,∠B的平分线与∠C的外角的平分线交于点P,PD⊥ AC于点D,PH⊥BA于点H.(1)若点P到直线BA的距离是5cm,求点P到直线BC的距离;(2)求证:点P在∠HAC的平分线上.
课外作业
2.如图,已知CD⊥AB,BE⊥AC,垂足分别为点D,E,BE,CD相交于点O,连接AO.求证:(1)当∠l=∠2时,OB=OC;
(2)当OB=OC时,∠1=∠2.
2.如图,已知CD⊥AB,BE⊥AC,垂足分别为点D,E,BE,CD相交于点O,连接AO.求证:(1)当∠l=∠2时,OB=OC;
(2)当OB=OC时,∠1=∠2.
3.已知∠MAN= I20°,AC平分∠MAN,点B,D分别在AN ,AM上,
(1)如图①,若∠ABC=∠ADC= 90°,请你探究线段AD,AB,AC之间的数量关系,并证明;(2)如图②,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
3.已知∠MAN= I20°,AC平分∠MAN,点B,D分别在AN ,AM上,(2)如图②,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
八年级下
1.4 角平分线第2课时三角形的内角平分线
活动1 分别画出下列三角形三个内角的平分线,你发现了什么?
三角形的内角平分线
发现:三角形的三条角平分线相交于一点.
活动2 分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的垂线段相等.
已知:如图,△ABC的角平分线BM,CN相交于点P,过点P作三边的垂线,垂足分别是点D,E,F.
求证:求证角A的平分线过点P,且PD=PE=PF
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,
点P在BM上,
∴PD=PE.同理PE=PF.
∴PD=PE=PF.∴点P在角A的平分线上,即三条角平分线相交于一点
即点P到三边AB,BC,CA的距离相等.
D
E
F
A
B
C
P
N
M
求证:三条角平分线相交于一点,且这点三条边的距离相等
P1
P2
P3
P4
l1
l2
l3
练习.如图, 直线l1、l2、l3表示三条互相交叉的公路, 现要建一个货物中转站, 要求它到三条公路的距离相等, 可选择的地址有几处? 画出它的位置.
例1.如图,在△ABC中,已知AC=BC, ∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)如果CD=4cm,AC的长;
E
D
A
B
C
(1)解:∵AD是△ABC的角平分线,DE⊥AB,垂足为E,∴DE=CD=4cm.
∵AC=BC,∴∠B=∠BAC.
∵∠C=90°,∴∠B=45°.∴BE=DE.
在等腰直角三角形BDE中,
(2)求证:AB=AC+CD.
E
D
A
B
C
(2)证明:由(1)的求解过程易知,
Rt△ACD≌Rt△AED(HL).
∴AC=AE.
∵BE=DE=CD,
∴AB=AE+BE=AC+CD.
例1.如图,在△ABC中,已知AC=BC, ∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
解:连接OC
M
E
N
A
B
C
P
O
D
例2:如图,在直角△ABC中,AC=BC,∠C=90°,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4,若△ABC的周长为32,求△ABC的面积.
解:点P在∠AOB的平分线上.
理由如下:过点P分别作PD⊥OA于点D,PE⊥OB于点E.
∵S四边形OMPG=S四边形OFPN,
∴S四边形OMPG-S四边形OMPF=S四边形OFPN-S四边形OMPF,
即S△FPG=S△MPN.
∵FG=MN,∴PD=PE.
又PD⊥OA,PE⊥OB,
∴点P在∠AOB的平分线上.
例3 如图,点F,G是OA上的两点,点M,N是OB上的两点,且FG=MN,四边形OMPG的面积与四边形OFPN的面积相等.那么点P是否在∠AOB的平分线上?请说明理由.
习题1.10
1.证明∵∠C=90°,∠B=30°,
∴∠BAC=60°.
∵AD平分∠BAC,
∴∠DAC=∠BAD=30°.
∵∠B=30°,
∴∠BAD=∠B=30°.
∴BD=AD.
∵∠C=90°,∠DAC=30°,
∴AD=2CD.∴BD=2CD.
2.证明如图所示,过点F作FG⊥AD,FH⊥AE,FI⊥BC.
∵BF是∠DBC的平分线,∴FG=FI.
同理,FH=FI.∴FG=FH.
∴点F在∠DAE的平分线上.
3.证明(1)∵P是∠AOB平分线上的一点,PC⊥OA,PD⊥OB,∴PC=PD.
又∵OP=OP,∴Rt△OCP≌Rt△ODP.
∴OC=OD.
(2)∵OC=OD,∠COP=∠DOP,
∴OP是CD的垂直平分线.
4.解(1)如图,作∠BAC的角平分线AF或作∠BAC的外角∠CAE的外角平分线AN,则直线AF或直线AN上任意一点(A除外)都满足到AB,AC的距离相等,可以修建油库.
(2)如图,作∠BAC的角平分线,作∠BCA的角平分线,两角平分线交于一点P,P点是修建油库的位置.
1.三角形三条角平分线的性质定理:三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等.?
2.三角形三个内角平分线的交点只有一个,实际作图时,只需作出两个角的平分线,第三个角的平分线必过这两条角平分线的交点.
3.利用面积法求距离的方法:三角形角平分线交点与三个顶点的连线,把原三角形分割成了三个小三角形,利用小三角形的面积之和等于原三角形的面积,是求角平分线交点到三边距离的常用方法.
归纳总结
1.如图,在△ABC中,∠B的平分线与∠C的外角的平分线交于点P,PD⊥ AC于点D,PH⊥BA于点H.(1)若点P到直线BA的距离是5cm,求点P到直线BC的距离;(2)求证:点P在∠HAC的平分线上.
课外作业
2.如图,已知CD⊥AB,BE⊥AC,垂足分别为点D,E,BE,CD相交于点O,连接AO.求证:(1)当∠l=∠2时,OB=OC;
(2)当OB=OC时,∠1=∠2.
2.如图,已知CD⊥AB,BE⊥AC,垂足分别为点D,E,BE,CD相交于点O,连接AO.求证:(1)当∠l=∠2时,OB=OC;
(2)当OB=OC时,∠1=∠2.
3.已知∠MAN= I20°,AC平分∠MAN,点B,D分别在AN ,AM上,
(1)如图①,若∠ABC=∠ADC= 90°,请你探究线段AD,AB,AC之间的数量关系,并证明;(2)如图②,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
3.已知∠MAN= I20°,AC平分∠MAN,点B,D分别在AN ,AM上,(2)如图②,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,给出证明;若不成立,请说明理由.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
