1.1.1 等腰三角形的判定与反证法 课件(共24张PPT)
文档属性
| 名称 | 1.1.1 等腰三角形的判定与反证法 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 00:00:00 | ||
图片预览








文档简介
数学北师大版
八年级下
1.1.1 等腰三角形
第3课时等腰三角形的判定与反证法
等腰三角形性质定理的内容是什么?这个命题
的题设和结论分别是什么?
我们把性质定理的条件和结论反过来还成立么?
如果一个三角形有两个角相等,那么这两个角所对的边也相等?
等边对等角
条件:等腰三角形,结论:两底角相等
已知:在△ABC中,∠B=∠C,
求证:AB=AC.
证明:如图,过点A作AD⊥BC于点D.
则∠ADB=∠ADC.
∵在△ABD与△ACD中,
∠B=∠C ,∠ADB=∠ADC, AD=AD ,
∴△ABD≌△ACD(AAS),
∴AB=AC.
C
B
A
分析:只要构造两个全等的三角形,使AB与AC成为对应边就可以了. 作角A的平分线,或作BC上的高,都可以把△ABC分成两个全等的三角形.
D
定理:有两个角相等的三角形是等腰三角形.
(等角对等边.)
等腰三角形的判定定理:
在△ABC中
∵∠B=∠C(已知),
∴AB=AC(等角对等边).
几何语言
A
C
B
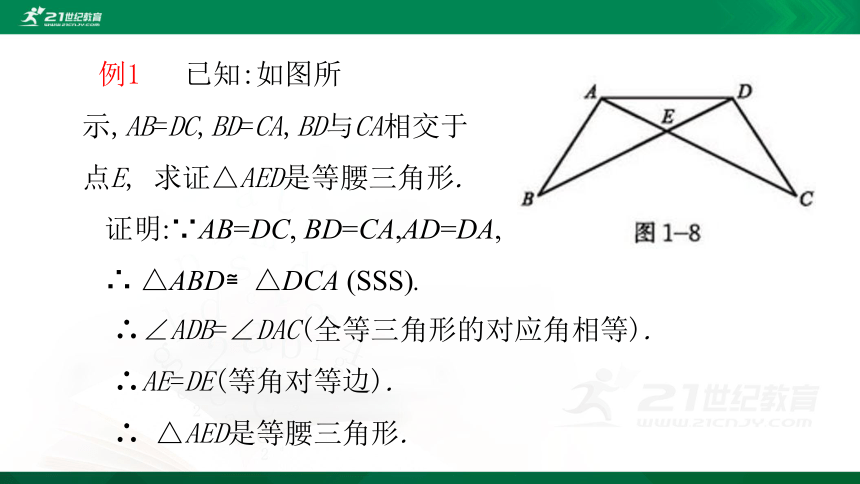
例1 已知:如图所示,AB=DC,BD=CA,BD与CA相交于点E, 求证△AED是等腰三角形.
证明:∵AB=DC, BD=CA,AD=DA,
∴ △ABD≌△DCA (SSS).
∴∠ADB=∠DAC(全等三角形的对应角相等).
∴AE=DE(等角对等边).
∴ △AED是等腰三角形.
例2 如图,在△ABC中,AB=AC,∠ABC和∠ACB的平分线交于点O.过O作EF∥BC交AB于E,交AC于F.请你写出图中所有等腰三角形,并探究EF、BE、FC之间的关系;
∴∠2=∠ABO ∠3=∠ACO
解:EF=BE+CF
A
B
C
O
E
F
1
3
2
4
理由:∵ EF∥BC
∴∠1=∠2 ∠3=∠4
∵ BO、CO分别平分∠ABC、∠ACB
∴∠1=∠ABO ∠4=∠ACO
∴CF=OF
∵ EF=EO+FO
∴EF=BE+CF
∴BE=OE
练习1 如图,∠A =36°,∠DBC =36°,∠C =72°,图中一共有几个等腰三角形?找出其中的一个等腰三角形给予证明.
A
B
C
D
证明:△ABC是等腰三角形.
在△ABC中,∵∠A=36°,∠C=72°,
∴∠ABC=180°-(72°+36°)=72°.
∵∠C=∠ABC,
∴AB=AC,
∴△ABC是等腰三角形。
有3个,分别是△ABC,△ABD,△DBC
2.如图所示,已知AB=AC,E,D分别在AB,AC上,BD与CE交于点F,且∠ABD=∠ACE,求证BF=CF.
证明:连接BC,∵AB=AC,
∴∠ABC=∠ACB.
∵∠ABD=∠ACE,
∴∠FBC=∠FCB,
∴FB=FC.
3.如图所示,在△ABC中,BA=BC,点D是AB延长线上一点,DF⊥AC于F交BC于E,求证△DBE是等腰三角形.
证明:∵BA=BC,∴∠A=∠C.
∵DF⊥AC,∴∠C+∠FEC=90°,∠A+∠D=90°.
∴∠FEC=∠D. ∵∠FEC=∠BED,∴∠BED=∠D.
∴BD=BE,即△DBE是等腰三角形.
想一想
小明说,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.你认为这个结论成立吗?如果成立,你能证明它吗?
我们来看一位同学的想法:
如图,在△ABC中,已知∠B≠∠C,此时AB与AC要么相等,要么不相等.
假设AB=AC,那么根据“等边对等角”定理可得∠C=∠B,但已知条件是∠B≠∠C.“∠C=∠B”与已知条件“∠B≠∠C”相矛盾,因此 AB≠AC
C
B
A
再如,我们要证明△ABC中不可能有两个直角,也可以采用这位同学的证法.
在上面的证法中,都是先假设命题的结论不成立,然后由此推导出了与已知或公理或已证明过的定理相矛盾,从而证明命题的结论一定成立.我们把它叫做反证法.
证明:假设∠A、∠B、∠C中有两个角是直角,设∠A=∠B=90°,则
∠A+∠B+∠C=90°+90°+∠C>180°.
这与三角形内角和定理矛盾,
所以∠A=∠B=90°不成立.
所以一个三角形中不能有两个角是直角.
反证法
先假设命题的结论不成立,然后推导出与定义、公理、已证定理或已知条件相矛盾的结果,从而证明命题的结论一定成立。这种证明方法称为反证法(reduction to absurdity)。
例1.证明:如果a1,a2,a3,a4,a5都是正数,且a1+a2+a3+a4+a5=1,那么,这五个数中至少有一个大于或等于1/5.
用反证法来证:
证明:假设这五个数全部小于1/5,那么这五个数的和a1+a2+a3+a4+a5就小于1.这与已知这五个数的和a1+a2+a3+a4+a5=1相矛盾.因此假设不成立, 原命题成立,即这五个数中至少有一个大于或等于1/5.
练习1.用反证法证明:△ABC中至少有一个内角小于或等于60°.
证明:假设在△ABC中,∠A,∠B,∠C均大于60°,设∠A>60°,∠B>60°,∠C>60°,
则∠A+∠B+∠C>180°,这与三角形内角和等于180°矛盾.所以假设不成立,故△ABC中至少有一个内角小于或等于60°.
2.用反证法证明命题“在三角形中,至多有一个内角是直角”时,应先假设( )
A.至少有一个内角是直角
B.至少有两个内角是直角
C.至多有一个内角是直角
D.至多有两个内角是直角
3.请举反例说明命题“对于任意实数x,x2+5x+5的值总是正数”是假命题.你举的反例是____.(写出一个x的值即可)
B
-2
提高训练:如图所示,在△ABC中,
已知∠ABC=∠ACB,
BO平分∠ABC,CO平分∠ACB.
(1)想想看,你能得到什么结论?
(2)若过点O作一直线EF和边BC平行,与AB交于点E,与AC交于点F,则图②中有哪几个等腰三角形?线段EF和EB,FC之间有怎样的关系?
(3)若∠ABC≠∠ACB,其他条件不变,图③中是否还有等腰三角形?(2)中第二问的关系是否还存在?写出你的理由.
解:(1)△OBC是等腰三角形(BC为底)或
∠BOC=90°+ ∠A
(2)等腰三角形有△ABC,△OBC,△BOE,△OCF,△AEF.EF=EB+FC
(3)等腰三角形有△BOE,△COF,仍有EF=EB+FC.理由:∵BO,CO分别平分∠ABC,∠ACB,∴∠EBO=∠OBC,∠FCO=∠OCB.又∵EF∥BC,∴∠OBC=∠BOE,∠OCB=∠COF,∴∠BOE=∠EBO,∠COF=∠FCO,∴EB=EO,FC=FO.∴EF=EO+FO=EB+FC
1.有两个角相等的三角形是等腰三角形.
(等角对等边.)
本课小结
2.反证法
课后作业:1.如图,在△ABC中,AB=AC=2,
∠B=∠C=40°,点D在线段BC上运动(D不
与B,C重合),连接AD,作∠ADE=40°,
DE交线段AC于点E.
(1)当∠BDA=115°时,∠EDC=________,
∠DEC=________;点D从B向C运动时,∠BDA逐渐变________(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?
若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
(2)当DC=2时,△ABD≌△DCE.理由:∵∠C=40°,
∴∠DEC+∠EDC=140°.又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,∴∠ADB=∠DEC.
又∵AB=DC=2,∴△ABD≌△DCE(AAS)
25°
115°
小
课后作业:1,如图,在△ABC中,AB=AC=2,
∠B=∠C=40°,点D在线段BC上运动(D不
与B,C重合),连接AD,作∠ADE=40°,
DE交线段AC于点E.
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?
若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
(3)当∠BDA的度数为110°或80°时,△ADE的形状是
等腰三角形.理由:当∠BDA=110°时,∠ADC=70°.
∵∠C=40°,∴∠DAC=180°-∠ADC-∠C
=180°-70°-40°=70°,
∴∠AED=180°-∠DAC-∠ADE=180°-70°-40°=70°,
∴∠AED=∠DAE,∴AD=ED,∴△ADE的形状是等腰三角形.
当∠BDA=80°时,∠ADC=100°.
∴∠DAC=180°-∠ADC-∠C=180°-100°-40°=40°,
∴∠DAE=∠ADE,∴AE=DE,∴△ADE的形状是等腰三角形
2.如图,在△ABC中,∠BAC=90°,
AD⊥BC于点D,BE平分∠ABC交AD于F,求证:△AEF是等腰三角形。
证明:∵AD⊥BC
∴∠ADB=90°
∴∠FBD+∠BFD=90O
又∵BE平分∠ABC
∴∠ABE=∠CBE
∵ ∠BAC=90°,
∴∠ABE+∠AEF=90O
又∵∠AFE= ∠BFD
∴∠AFE=∠AEF
∴△AEF是等腰三角形
3.阅读并证明:在一个三角形中,较大的角所对的边较大,较小的角所对的边较小,简称为大角对大边,小角对小边,可用等腰三角形的判定定理给出证明,
如图,在△ABC中,∠A>∠B,求证:BC>AC.
证明:在∠BAC的内部作∠BAD=∠B,交BC于点D。
D
∵∠BAD=∠B ∴AD=BD 又∵在△ACD中,AD+CD>AC 即BD+CD>AC ∴BC>AC
4.(7分)如图,将长方形ABCD沿对角线BD翻折,点C落在点E的位置,BE交AD于点F.
求证:重叠部分(即△BDF)是等腰三角形.
证明:∵四边形ABCD是长方形,∴AD∥BC,∴∠ADB=∠DBC.
又∵△BDE与△BDC关于BD所在的直线对称,∴∠FBD=∠DBC,
.∴∠ADB=∠FBD,∴DF=BF,
∴重叠部分(即△BDF)是等腰三角形
5. 如图,上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测∠NAC=40°∠NBC=80°求从B处到灯塔C的距离。
解:∵∠NBC=∠A+∠C
∴∠C=80°- 40°= 40°
∴ ∠C = ∠A
∴ BA=BC(等角对等边)
∵AB=20(12-10)=40
∴BC=40
答:B处到达灯塔C的距离是40海里。
80°
40°
N
B
A
C
北
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
八年级下
1.1.1 等腰三角形
第3课时等腰三角形的判定与反证法
等腰三角形性质定理的内容是什么?这个命题
的题设和结论分别是什么?
我们把性质定理的条件和结论反过来还成立么?
如果一个三角形有两个角相等,那么这两个角所对的边也相等?
等边对等角
条件:等腰三角形,结论:两底角相等
已知:在△ABC中,∠B=∠C,
求证:AB=AC.
证明:如图,过点A作AD⊥BC于点D.
则∠ADB=∠ADC.
∵在△ABD与△ACD中,
∠B=∠C ,∠ADB=∠ADC, AD=AD ,
∴△ABD≌△ACD(AAS),
∴AB=AC.
C
B
A
分析:只要构造两个全等的三角形,使AB与AC成为对应边就可以了. 作角A的平分线,或作BC上的高,都可以把△ABC分成两个全等的三角形.
D
定理:有两个角相等的三角形是等腰三角形.
(等角对等边.)
等腰三角形的判定定理:
在△ABC中
∵∠B=∠C(已知),
∴AB=AC(等角对等边).
几何语言
A
C
B
例1 已知:如图所示,AB=DC,BD=CA,BD与CA相交于点E, 求证△AED是等腰三角形.
证明:∵AB=DC, BD=CA,AD=DA,
∴ △ABD≌△DCA (SSS).
∴∠ADB=∠DAC(全等三角形的对应角相等).
∴AE=DE(等角对等边).
∴ △AED是等腰三角形.
例2 如图,在△ABC中,AB=AC,∠ABC和∠ACB的平分线交于点O.过O作EF∥BC交AB于E,交AC于F.请你写出图中所有等腰三角形,并探究EF、BE、FC之间的关系;
∴∠2=∠ABO ∠3=∠ACO
解:EF=BE+CF
A
B
C
O
E
F
1
3
2
4
理由:∵ EF∥BC
∴∠1=∠2 ∠3=∠4
∵ BO、CO分别平分∠ABC、∠ACB
∴∠1=∠ABO ∠4=∠ACO
∴CF=OF
∵ EF=EO+FO
∴EF=BE+CF
∴BE=OE
练习1 如图,∠A =36°,∠DBC =36°,∠C =72°,图中一共有几个等腰三角形?找出其中的一个等腰三角形给予证明.
A
B
C
D
证明:△ABC是等腰三角形.
在△ABC中,∵∠A=36°,∠C=72°,
∴∠ABC=180°-(72°+36°)=72°.
∵∠C=∠ABC,
∴AB=AC,
∴△ABC是等腰三角形。
有3个,分别是△ABC,△ABD,△DBC
2.如图所示,已知AB=AC,E,D分别在AB,AC上,BD与CE交于点F,且∠ABD=∠ACE,求证BF=CF.
证明:连接BC,∵AB=AC,
∴∠ABC=∠ACB.
∵∠ABD=∠ACE,
∴∠FBC=∠FCB,
∴FB=FC.
3.如图所示,在△ABC中,BA=BC,点D是AB延长线上一点,DF⊥AC于F交BC于E,求证△DBE是等腰三角形.
证明:∵BA=BC,∴∠A=∠C.
∵DF⊥AC,∴∠C+∠FEC=90°,∠A+∠D=90°.
∴∠FEC=∠D. ∵∠FEC=∠BED,∴∠BED=∠D.
∴BD=BE,即△DBE是等腰三角形.
想一想
小明说,在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.你认为这个结论成立吗?如果成立,你能证明它吗?
我们来看一位同学的想法:
如图,在△ABC中,已知∠B≠∠C,此时AB与AC要么相等,要么不相等.
假设AB=AC,那么根据“等边对等角”定理可得∠C=∠B,但已知条件是∠B≠∠C.“∠C=∠B”与已知条件“∠B≠∠C”相矛盾,因此 AB≠AC
C
B
A
再如,我们要证明△ABC中不可能有两个直角,也可以采用这位同学的证法.
在上面的证法中,都是先假设命题的结论不成立,然后由此推导出了与已知或公理或已证明过的定理相矛盾,从而证明命题的结论一定成立.我们把它叫做反证法.
证明:假设∠A、∠B、∠C中有两个角是直角,设∠A=∠B=90°,则
∠A+∠B+∠C=90°+90°+∠C>180°.
这与三角形内角和定理矛盾,
所以∠A=∠B=90°不成立.
所以一个三角形中不能有两个角是直角.
反证法
先假设命题的结论不成立,然后推导出与定义、公理、已证定理或已知条件相矛盾的结果,从而证明命题的结论一定成立。这种证明方法称为反证法(reduction to absurdity)。
例1.证明:如果a1,a2,a3,a4,a5都是正数,且a1+a2+a3+a4+a5=1,那么,这五个数中至少有一个大于或等于1/5.
用反证法来证:
证明:假设这五个数全部小于1/5,那么这五个数的和a1+a2+a3+a4+a5就小于1.这与已知这五个数的和a1+a2+a3+a4+a5=1相矛盾.因此假设不成立, 原命题成立,即这五个数中至少有一个大于或等于1/5.
练习1.用反证法证明:△ABC中至少有一个内角小于或等于60°.
证明:假设在△ABC中,∠A,∠B,∠C均大于60°,设∠A>60°,∠B>60°,∠C>60°,
则∠A+∠B+∠C>180°,这与三角形内角和等于180°矛盾.所以假设不成立,故△ABC中至少有一个内角小于或等于60°.
2.用反证法证明命题“在三角形中,至多有一个内角是直角”时,应先假设( )
A.至少有一个内角是直角
B.至少有两个内角是直角
C.至多有一个内角是直角
D.至多有两个内角是直角
3.请举反例说明命题“对于任意实数x,x2+5x+5的值总是正数”是假命题.你举的反例是____.(写出一个x的值即可)
B
-2
提高训练:如图所示,在△ABC中,
已知∠ABC=∠ACB,
BO平分∠ABC,CO平分∠ACB.
(1)想想看,你能得到什么结论?
(2)若过点O作一直线EF和边BC平行,与AB交于点E,与AC交于点F,则图②中有哪几个等腰三角形?线段EF和EB,FC之间有怎样的关系?
(3)若∠ABC≠∠ACB,其他条件不变,图③中是否还有等腰三角形?(2)中第二问的关系是否还存在?写出你的理由.
解:(1)△OBC是等腰三角形(BC为底)或
∠BOC=90°+ ∠A
(2)等腰三角形有△ABC,△OBC,△BOE,△OCF,△AEF.EF=EB+FC
(3)等腰三角形有△BOE,△COF,仍有EF=EB+FC.理由:∵BO,CO分别平分∠ABC,∠ACB,∴∠EBO=∠OBC,∠FCO=∠OCB.又∵EF∥BC,∴∠OBC=∠BOE,∠OCB=∠COF,∴∠BOE=∠EBO,∠COF=∠FCO,∴EB=EO,FC=FO.∴EF=EO+FO=EB+FC
1.有两个角相等的三角形是等腰三角形.
(等角对等边.)
本课小结
2.反证法
课后作业:1.如图,在△ABC中,AB=AC=2,
∠B=∠C=40°,点D在线段BC上运动(D不
与B,C重合),连接AD,作∠ADE=40°,
DE交线段AC于点E.
(1)当∠BDA=115°时,∠EDC=________,
∠DEC=________;点D从B向C运动时,∠BDA逐渐变________(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?
若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
(2)当DC=2时,△ABD≌△DCE.理由:∵∠C=40°,
∴∠DEC+∠EDC=140°.又∵∠ADE=40°,
∴∠ADB+∠EDC=140°,∴∠ADB=∠DEC.
又∵AB=DC=2,∴△ABD≌△DCE(AAS)
25°
115°
小
课后作业:1,如图,在△ABC中,AB=AC=2,
∠B=∠C=40°,点D在线段BC上运动(D不
与B,C重合),连接AD,作∠ADE=40°,
DE交线段AC于点E.
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?
若可以,请直接写出∠BDA的度数.若不可以,请说明理由.
(3)当∠BDA的度数为110°或80°时,△ADE的形状是
等腰三角形.理由:当∠BDA=110°时,∠ADC=70°.
∵∠C=40°,∴∠DAC=180°-∠ADC-∠C
=180°-70°-40°=70°,
∴∠AED=180°-∠DAC-∠ADE=180°-70°-40°=70°,
∴∠AED=∠DAE,∴AD=ED,∴△ADE的形状是等腰三角形.
当∠BDA=80°时,∠ADC=100°.
∴∠DAC=180°-∠ADC-∠C=180°-100°-40°=40°,
∴∠DAE=∠ADE,∴AE=DE,∴△ADE的形状是等腰三角形
2.如图,在△ABC中,∠BAC=90°,
AD⊥BC于点D,BE平分∠ABC交AD于F,求证:△AEF是等腰三角形。
证明:∵AD⊥BC
∴∠ADB=90°
∴∠FBD+∠BFD=90O
又∵BE平分∠ABC
∴∠ABE=∠CBE
∵ ∠BAC=90°,
∴∠ABE+∠AEF=90O
又∵∠AFE= ∠BFD
∴∠AFE=∠AEF
∴△AEF是等腰三角形
3.阅读并证明:在一个三角形中,较大的角所对的边较大,较小的角所对的边较小,简称为大角对大边,小角对小边,可用等腰三角形的判定定理给出证明,
如图,在△ABC中,∠A>∠B,求证:BC>AC.
证明:在∠BAC的内部作∠BAD=∠B,交BC于点D。
D
∵∠BAD=∠B ∴AD=BD 又∵在△ACD中,AD+CD>AC 即BD+CD>AC ∴BC>AC
4.(7分)如图,将长方形ABCD沿对角线BD翻折,点C落在点E的位置,BE交AD于点F.
求证:重叠部分(即△BDF)是等腰三角形.
证明:∵四边形ABCD是长方形,∴AD∥BC,∴∠ADB=∠DBC.
又∵△BDE与△BDC关于BD所在的直线对称,∴∠FBD=∠DBC,
.∴∠ADB=∠FBD,∴DF=BF,
∴重叠部分(即△BDF)是等腰三角形
5. 如图,上午10 时,一条船从A处出发以20海里每小时的速度向正北航行,中午12时到达B处,从A、B望灯塔C,测∠NAC=40°∠NBC=80°求从B处到灯塔C的距离。
解:∵∠NBC=∠A+∠C
∴∠C=80°- 40°= 40°
∴ ∠C = ∠A
∴ BA=BC(等角对等边)
∵AB=20(12-10)=40
∴BC=40
答:B处到达灯塔C的距离是40海里。
80°
40°
N
B
A
C
北
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
