1.1.2 等腰三角形的特殊性质与等边三角形 课件(共18张PPT)
文档属性
| 名称 | 1.1.2 等腰三角形的特殊性质与等边三角形 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 07:37:28 | ||
图片预览





文档简介
数学北师大版
八年级下
1.1.1 等腰三角形
第2课时等腰三角形的特殊性质与等边三角形
A
E
B
D
C
1
2
等腰三角形两底角的平分线相等
证明:∵AB=AC(已知)
∴∠ABC=∠ACB(等边对等角)
又∵BD、CE分别是∠ABC、∠ACB的平分线
∴∠1=? ∠ABC ,∠2= ∠ACB
∴∠1=∠2
在△ABD和△ACE中
∠1=∠2(已证)
AB=AC(已知)
∠A=∠A(公共角)
已知:如图,在△ABC中,AB=AC,BD、CE是△ABC的角平分线。求证:BD=CE
∴△ABD≌△ACE(ASA)
∴BD=CE(全等三角形的对应边相等)
已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线.
求证:BD=CE.
方法二证明:∵AB=AC,∴∠ABC=∠ACB(等边对等角).
∵∠1= ∠ABC,∠2= ∠ACB,∴∠1=∠2.
在△BDC和△CEB中,
∵∠ACB=∠ABC,BC=CB,∠1=∠2.
∴△BDC≌△CEB(ASA).
∴BD=CE(全等三角形的对应边相等).
A
E
B
D
C
1
2
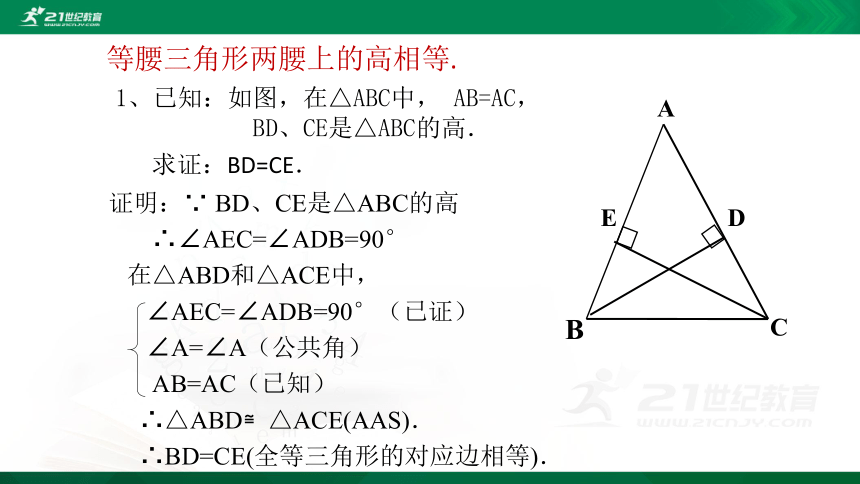
1、已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的高.
等腰三角形两腰上的高相等.
求证:BD=CE.
E
D
C
B
A
证明:∵ BD、CE是△ABC的高
∴∠AEC=∠ADB=90°
在△ABD和△ACE中,
∠AEC=∠ADB=90°(已证)
∠A=∠A(公共角)
AB=AC(已知)
∴△ABD≌△ACE(AAS).
∴BD=CE(全等三角形的对应边相等).
2、已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的中线.
等腰三角形两腰上的中线相等.
求证:BD=CE.
证明:∵AB=AC(已知)
又∵BD、CE是△ABC的中线
∴AE= AB AD= AC
∴AE=AD
在△ABD和△ACE中,
AE=AD(已证)
∠A=∠A(公共角)
AB=AC(已知)
∴△ABD≌△ACE(SAS).
.
∴BD=CE(全等三角形的对应边相等)
A
C
B
M
N
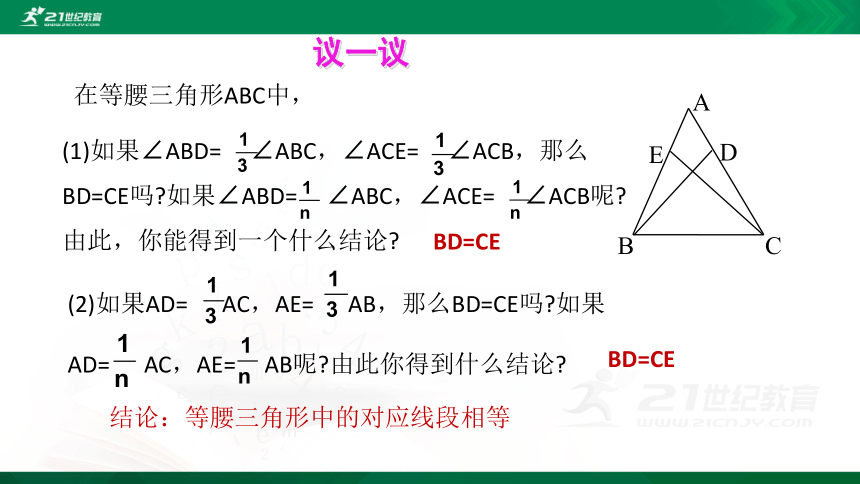
议一议
E
D
C
B
A
在等腰三角形ABC中,
(1)如果∠ABD= ∠ABC,∠ACE= ∠ACB,那么BD=CE吗?如果∠ABD= ∠ABC,∠ACE= ∠ACB呢?由此,你能得到一个什么结论?
结论:等腰三角形中的对应线段相等
(2)如果AD= AC,AE= AB,那么BD=CE吗?如果AD= AC,AE= AB呢?由此你得到什么结论?
BD=CE
BD=CE
证明:在△ABC中,
∵AB=AC,
∴∠B=∠C(等边对等角)
同理:∠C=∠A
∴∠A=∠B=∠C(等量代换)
又∵∠A+∠B+∠C=180°
∴∠A=∠B=∠C=60°
定理:等边三角形三个内角都相等,且每个内角都等于60°
已知:如图,在△ABC中,AB=BC=AC
求证:∠A=∠B=∠C=60°
A
B
C
等边三角形的性质:
名称
图 形
性 质
等
边
三
角
形
边
角
顶角平分线
底边中线
底边高线
对称性
三个内角相等,且为60°
三线合一
三条边都相等
轴对称图形,三条对称轴
随堂练习 及时巩固
一、如图,已知△ABC和△BDE都是等边三角形,
求证:AE=CD
A
B
C
D
E
证明:
∵ △ABC和△BDE都是等边三角形
∴AB=BC,∠ABC=∠DBE=60°,BE=BD
∴ △ABE≌△CBD
∴AE=CD
二、如图,等边△ABC中,CE为BC的延长线,且CE=CD,求∠E等于多少度??
解:∵△ABC是等边三角形
∴∠ABC=∠A=∠ACB=60°
∵ CE=CD(已知)
∴∠E=∠EDC(等边对等角)
又∵∠ACB=∠E+∠EDC=60°
∴∠E=∠EDC=30°
提高训练(1)如图①,在Rt△ABC中,∠ACB=90°,
点D,E在边AB上,且AD=AC,BE=BC,求∠DCE的度数;
(2)如图②,在△ABC中,∠ACB=40°,点D,E在
直线AB上,且AD=AC,BE=BC,则∠DCE=____;
(3)在△ABC中,∠ACB=n°(0直线AB上,且AD=AC,BE=BC,求∠DCE的度数
(直接写出答案,用含n的式子表示).
解:(1)∵AD=AC,BC=BE,∴∠ACD=∠ADC,∠BCE=∠BEC,∴∠ACD=(180°-∠A)÷2,∠BCE=(180°-∠B)÷2.
∵∠A+∠B=90°,∴∠ACD+∠BCE=180°-(∠A+∠B)÷2=180°-45°=135°,∴∠DCE=∠ACD+∠BCE-∠ACB=135°-90°=45°
(2)如图②,在△ABC中,∠ACB=40°,点D,E在
直线AB上,且AD=AC,BE=BC,则∠DCE=____;
(3)在△ABC中,∠ACB=n°(0直线AB上,且AD=AC,BE=BC,求∠DCE的度数
(直接写出答案,用含n的式子表示).
110°
(3)①如题图①,∠DCE=90°- n°; ②如题图②,∠DCE=90°+ n°;
③如图③,∠DCE= n°; ④如图④,∠DCE= n°; ⑤如图⑤,∠DCE= n°
等边三角形的性质:
三个内角都相等,且为60°
三线合一
三条边都相等
轴对称图形,有三条对称轴
等腰三角形两底角的平分线相等
等腰三角形两腰上的高相等
等腰三角形两腰上的中线相等
等腰三角形中的对应线段相等
本课小结
课外作业:1、如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以PB为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.
解:猜想:AP=CQ.证明:∵△ABC是等边三角形,∴∠ABC=60°,
∵∠PBQ=60°,∴∠ABC=∠PBQ,∴∠ABP=∠ABC-∠PBC=∠PBQ-∠PBC=∠CBQ.在△ABP和△CBQ中,
∵AB=CB,∠ABP=∠CBQ,BP=BQ,
∴△ABP≌△CBQ,∴AP=CQ
2、(12分)如图,在等边△ABC中,D是BC上的一点,延长AD至E,使AE=AC,∠BAE的平分线交△ABC的高BF于点O.求∠E的度数.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
八年级下
1.1.1 等腰三角形
第2课时等腰三角形的特殊性质与等边三角形
A
E
B
D
C
1
2
等腰三角形两底角的平分线相等
证明:∵AB=AC(已知)
∴∠ABC=∠ACB(等边对等角)
又∵BD、CE分别是∠ABC、∠ACB的平分线
∴∠1=? ∠ABC ,∠2= ∠ACB
∴∠1=∠2
在△ABD和△ACE中
∠1=∠2(已证)
AB=AC(已知)
∠A=∠A(公共角)
已知:如图,在△ABC中,AB=AC,BD、CE是△ABC的角平分线。求证:BD=CE
∴△ABD≌△ACE(ASA)
∴BD=CE(全等三角形的对应边相等)
已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的角平分线.
求证:BD=CE.
方法二证明:∵AB=AC,∴∠ABC=∠ACB(等边对等角).
∵∠1= ∠ABC,∠2= ∠ACB,∴∠1=∠2.
在△BDC和△CEB中,
∵∠ACB=∠ABC,BC=CB,∠1=∠2.
∴△BDC≌△CEB(ASA).
∴BD=CE(全等三角形的对应边相等).
A
E
B
D
C
1
2
1、已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的高.
等腰三角形两腰上的高相等.
求证:BD=CE.
E
D
C
B
A
证明:∵ BD、CE是△ABC的高
∴∠AEC=∠ADB=90°
在△ABD和△ACE中,
∠AEC=∠ADB=90°(已证)
∠A=∠A(公共角)
AB=AC(已知)
∴△ABD≌△ACE(AAS).
∴BD=CE(全等三角形的对应边相等).
2、已知:如图,在△ABC中, AB=AC,
BD、CE是△ABC的中线.
等腰三角形两腰上的中线相等.
求证:BD=CE.
证明:∵AB=AC(已知)
又∵BD、CE是△ABC的中线
∴AE= AB AD= AC
∴AE=AD
在△ABD和△ACE中,
AE=AD(已证)
∠A=∠A(公共角)
AB=AC(已知)
∴△ABD≌△ACE(SAS).
.
∴BD=CE(全等三角形的对应边相等)
A
C
B
M
N
议一议
E
D
C
B
A
在等腰三角形ABC中,
(1)如果∠ABD= ∠ABC,∠ACE= ∠ACB,那么BD=CE吗?如果∠ABD= ∠ABC,∠ACE= ∠ACB呢?由此,你能得到一个什么结论?
结论:等腰三角形中的对应线段相等
(2)如果AD= AC,AE= AB,那么BD=CE吗?如果AD= AC,AE= AB呢?由此你得到什么结论?
BD=CE
BD=CE
证明:在△ABC中,
∵AB=AC,
∴∠B=∠C(等边对等角)
同理:∠C=∠A
∴∠A=∠B=∠C(等量代换)
又∵∠A+∠B+∠C=180°
∴∠A=∠B=∠C=60°
定理:等边三角形三个内角都相等,且每个内角都等于60°
已知:如图,在△ABC中,AB=BC=AC
求证:∠A=∠B=∠C=60°
A
B
C
等边三角形的性质:
名称
图 形
性 质
等
边
三
角
形
边
角
顶角平分线
底边中线
底边高线
对称性
三个内角相等,且为60°
三线合一
三条边都相等
轴对称图形,三条对称轴
随堂练习 及时巩固
一、如图,已知△ABC和△BDE都是等边三角形,
求证:AE=CD
A
B
C
D
E
证明:
∵ △ABC和△BDE都是等边三角形
∴AB=BC,∠ABC=∠DBE=60°,BE=BD
∴ △ABE≌△CBD
∴AE=CD
二、如图,等边△ABC中,CE为BC的延长线,且CE=CD,求∠E等于多少度??
解:∵△ABC是等边三角形
∴∠ABC=∠A=∠ACB=60°
∵ CE=CD(已知)
∴∠E=∠EDC(等边对等角)
又∵∠ACB=∠E+∠EDC=60°
∴∠E=∠EDC=30°
提高训练(1)如图①,在Rt△ABC中,∠ACB=90°,
点D,E在边AB上,且AD=AC,BE=BC,求∠DCE的度数;
(2)如图②,在△ABC中,∠ACB=40°,点D,E在
直线AB上,且AD=AC,BE=BC,则∠DCE=____;
(3)在△ABC中,∠ACB=n°(0
(直接写出答案,用含n的式子表示).
解:(1)∵AD=AC,BC=BE,∴∠ACD=∠ADC,∠BCE=∠BEC,∴∠ACD=(180°-∠A)÷2,∠BCE=(180°-∠B)÷2.
∵∠A+∠B=90°,∴∠ACD+∠BCE=180°-(∠A+∠B)÷2=180°-45°=135°,∴∠DCE=∠ACD+∠BCE-∠ACB=135°-90°=45°
(2)如图②,在△ABC中,∠ACB=40°,点D,E在
直线AB上,且AD=AC,BE=BC,则∠DCE=____;
(3)在△ABC中,∠ACB=n°(0
(直接写出答案,用含n的式子表示).
110°
(3)①如题图①,∠DCE=90°- n°; ②如题图②,∠DCE=90°+ n°;
③如图③,∠DCE= n°; ④如图④,∠DCE= n°; ⑤如图⑤,∠DCE= n°
等边三角形的性质:
三个内角都相等,且为60°
三线合一
三条边都相等
轴对称图形,有三条对称轴
等腰三角形两底角的平分线相等
等腰三角形两腰上的高相等
等腰三角形两腰上的中线相等
等腰三角形中的对应线段相等
本课小结
课外作业:1、如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以PB为边作∠PBQ=60°,且BQ=BP,连接CQ.观察并猜想AP与CQ之间的大小关系,并证明你的结论.
解:猜想:AP=CQ.证明:∵△ABC是等边三角形,∴∠ABC=60°,
∵∠PBQ=60°,∴∠ABC=∠PBQ,∴∠ABP=∠ABC-∠PBC=∠PBQ-∠PBC=∠CBQ.在△ABP和△CBQ中,
∵AB=CB,∠ABP=∠CBQ,BP=BQ,
∴△ABP≌△CBQ,∴AP=CQ
2、(12分)如图,在等边△ABC中,D是BC上的一点,延长AD至E,使AE=AC,∠BAE的平分线交△ABC的高BF于点O.求∠E的度数.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
