3.2 用关系式表示的变量间关系 课件(共27张PPT)
文档属性
| 名称 | 3.2 用关系式表示的变量间关系 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 20:25:27 | ||
图片预览


文档简介
数学北师大版
七年级下
3.2用关系式表示的变量间关系
(1)如果△ABC的底边长为a,高为h,那么面积
S△ABC=__________________.
(2)如果梯形的上底、下底长分别为a、b,高
为h,那么面积S梯形=____________.
(3)圆柱的底面半径为r,高为h,体积V圆柱=
___________;圆锥底面的半径为r,高为
h,体积V圆锥=_______________.
复习交流
πr2h
πr2h
A
B
C
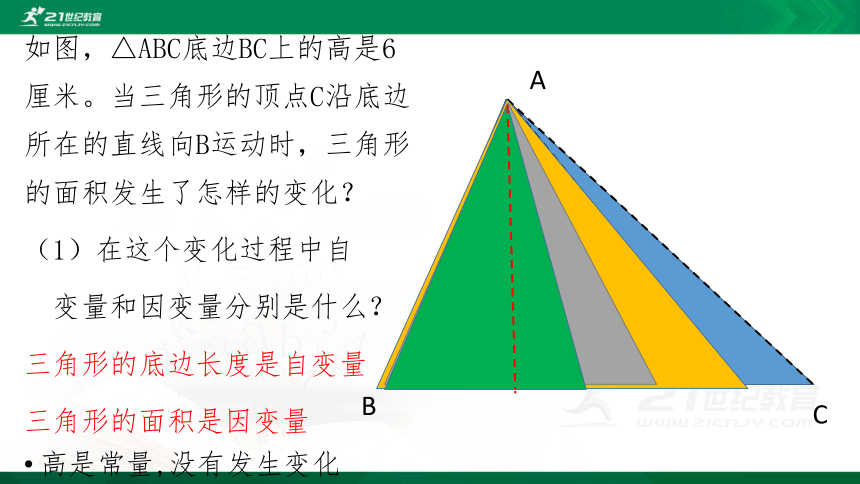
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
(1)在这个变化过程中自
变量和因变量分别是什么?
三角形的底边长度是自变量
三角形的面积是因变量
高是常量,没有发生变化
A
B
C
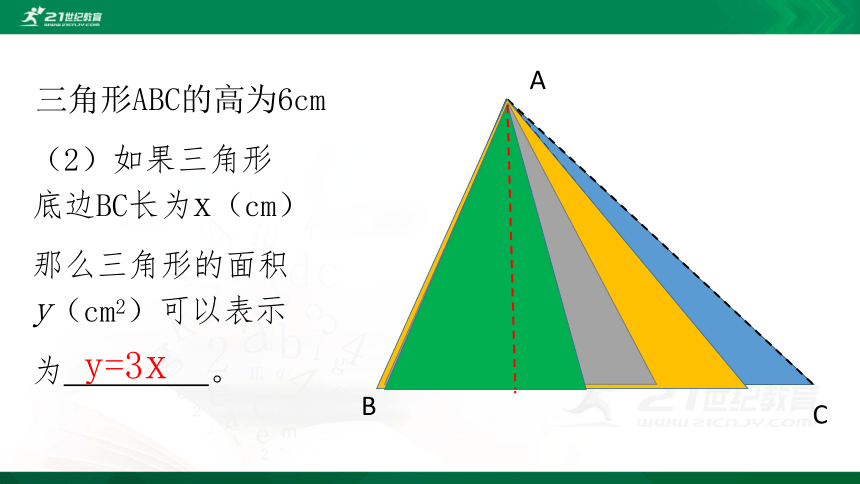
三角形ABC的高为6cm
(2)如果三角形底边BC长为x(cm)
那么三角形的面积y(cm2)可以表示
为 。
y=3x
A
B
C
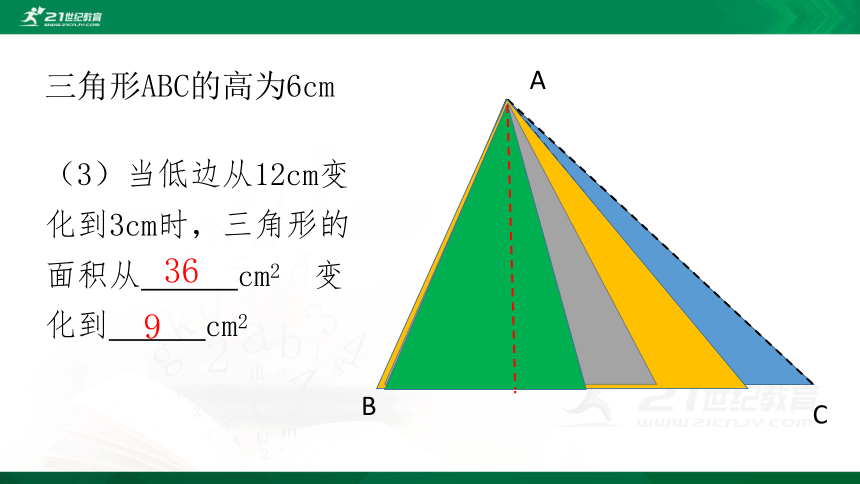
三角形ABC的高为6cm
(3)当低边从12cm变化到3cm时,三角形的面积从 cm2 变化到 cm2
36
9
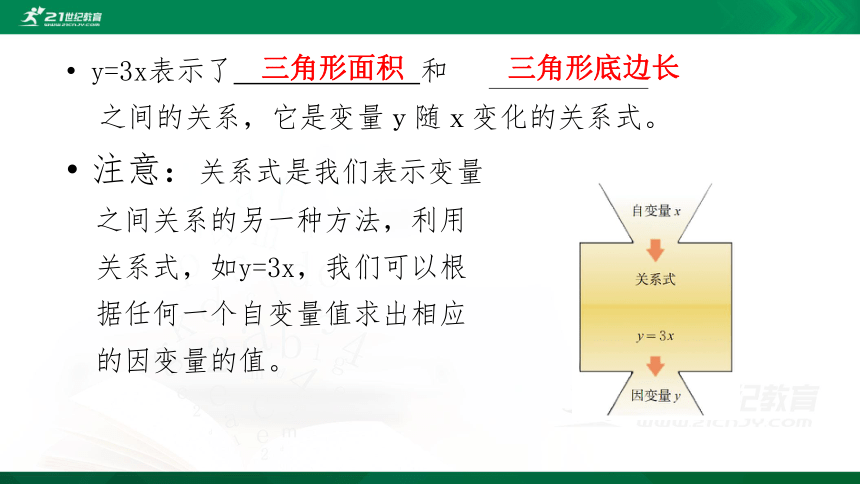
y=3x表示了 和
之间的关系,它是变量y随x变化的关系式。
注意:关系式是我们表示变量
之间关系的另一种方法,利用
关系式,如y=3x,我们可以根
据任何一个自变量值求出相应
的因变量的值。
三角形底边长
三角形面积
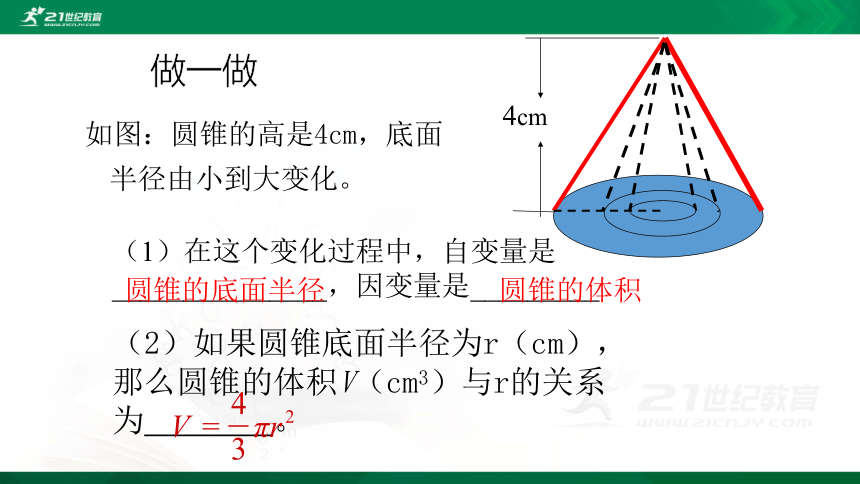
如图:圆锥的高是4cm,底面半径由小到大变化。
(2)如果圆锥底面半径为r(cm),那么圆锥的体积V(cm3)与r的关系为 。
(1)在这个变化过程中,自变量是_______________,因变量是_________
4cm
圆锥的底面半径
圆锥的体积
做一做
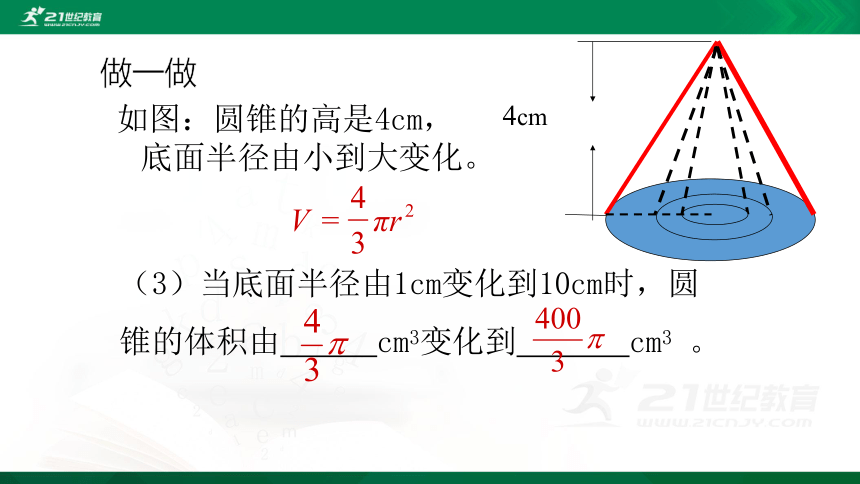
(3)当底面半径由1cm变化到10cm时,圆
锥的体积由 cm3变化到 cm3 。
4cm
如图:圆锥的高是4cm,底面半径由小到大变化。
做一做
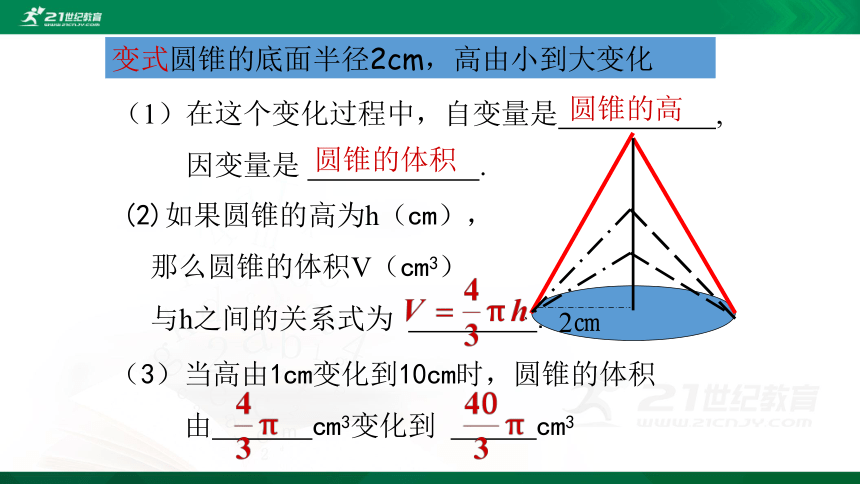
(1)在这个变化过程中,自变量是 ,
因变量是 .
2㎝
(2)如果圆锥的高为h(cm),
那么圆锥的体积V(cm3)
与h之间的关系式为 .
(3)当高由1cm变化到10cm时,圆锥的体积
由 cm3变化到 cm3
圆锥的高
圆锥的体积
变式圆锥的底面半径2cm,高由小到大变化
(1)家居用电的二氧化碳排放量可以用关系式表示为 _______ ,
其中的字母表示什么?
y = 0.785x
y 为家居用电的二氧化碳排放量 ;
议一议
低碳生活
x 为耗电量 。
排碳计算公式
家居用电的二氧化碳排放量(kg)
=耗电量(kw?h)×0.785
开私家车的二氧化碳排放量(kg)
=油耗升数(L)×2.7
家用天然气的二氧化碳排放量(kg)
=天然气使用量(m3)×0.19
家用自来水的二气化碳排放量(kg)
=自来水吨数(t)×0.91
(2)在上述关系式中,耗电量每增加
1 KW·h,二氧化碳排放量增加_________。当耗电量从1 KW·h增加到100 KW·h时,二氧化碳排 放量从_______增加
到_________。
0.785kg
0.785kg
78.5kg
低碳生活
排碳计算公式
家居用电的二氧化碳排放量(kg)
=耗电量(kw?h)×0.785
开私家车的二氧化碳排放量(kg)
=油耗升数(L)×2.7
家用天然气的二氧化碳排放量(kg)
=天然气使用量(m3)×0.19
家用自来水的二气化碳排放量(kg)
=自来水吨数(t)×0.91
(3)小明家本月用电大约100 KW·h,天然气10m3,自来水10t,油耗10L,请你计算一下小明家这几项的二氧化碳排放量。
低碳生活
排碳计算公式
家居用电的二氧化碳排放量(kg)
=耗电量(kw?h)×0.785
开私家车的二氧化碳排放量(kg)
=油耗升数(L)×2.7
家用天然气的二氧化碳排放量(kg)
=天然气使用量(m3)×0.19
家用自来水的二气化碳排放量(kg)
=自来水吨数(t)×0.91
+
+
+
=
随堂练习
1、在地球某地,温度T(℃)与高度d
(m)的关系可以近似地用
来表示,根据这个关系式,当
d的值分别是200,400,600,
800,1000时,计算相应的T值,
并用表格表示所得结果
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x(cm)
0
200
400
600
800
1000
y(cm2)
10
10
8.67
7.33
6.00
4.67
3.33
2.某弹簧的自然长度为3cm,在弹性限度内所挂的物体的重量x 每增加1 kg ,弹簧长度y增加0.5cm。
x/kg
1
2
3
4
5
……
y/cm
……
(1)依据上表数据,写出y与x之间的关系式。
3.5
4
4.5
5
5.5
(2)当物体的质量为6kg时,根据(1)的关 系式求出弹簧的长度。
y = 3+0.5x
y = 3+0.5x6=9
燃烧时间x/分
10
20
30
40
50
…
剩余长度y/cm
19
18
17
16
15
…
3.一支原长为20cm的蜡烛,点燃后,其剩余
长度y(cm)与燃烧时间x(分)之间的关系如
下表:
则剩余长度y(cm)与燃烧时间x(分)关系式为 。 估计这支蜡烛最多可燃烧 分。
200
4、如图所示,梯形上底的长是a ,下底的长是15,
高是8,上底变化时,梯形的面积随之改变。
(1)梯形面积S与上底长a之间的关系式是什么?
a
8
15
(2)用表格表示当a从10变到15时(每次增加1),S的相应值;
(1) S=4a+60
a
10
11
12
13
14
15
S
100
104
108
112
116
120
a
8
15
(4)当a=0时,S等于什么?此时它表示的什么?
(3)当a每增加1时,S如何变化?
(3) a每增加1时,S增加4.
(4)a=0时,S=60,
此时它表示的是三角形的面积.
课后作业
课本
1.直接做在书上的作业:知识技能1、2。
2.做在作业本上的作业:数学理解3.
3.需要实际调查的作业:问题解决4(以报告单形式上交)
备用习题
1
2
3
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
七年级下
3.2用关系式表示的变量间关系
(1)如果△ABC的底边长为a,高为h,那么面积
S△ABC=__________________.
(2)如果梯形的上底、下底长分别为a、b,高
为h,那么面积S梯形=____________.
(3)圆柱的底面半径为r,高为h,体积V圆柱=
___________;圆锥底面的半径为r,高为
h,体积V圆锥=_______________.
复习交流
πr2h
πr2h
A
B
C
如图,△ABC底边BC上的高是6厘米。当三角形的顶点C沿底边所在的直线向B运动时,三角形的面积发生了怎样的变化?
(1)在这个变化过程中自
变量和因变量分别是什么?
三角形的底边长度是自变量
三角形的面积是因变量
高是常量,没有发生变化
A
B
C
三角形ABC的高为6cm
(2)如果三角形底边BC长为x(cm)
那么三角形的面积y(cm2)可以表示
为 。
y=3x
A
B
C
三角形ABC的高为6cm
(3)当低边从12cm变化到3cm时,三角形的面积从 cm2 变化到 cm2
36
9
y=3x表示了 和
之间的关系,它是变量y随x变化的关系式。
注意:关系式是我们表示变量
之间关系的另一种方法,利用
关系式,如y=3x,我们可以根
据任何一个自变量值求出相应
的因变量的值。
三角形底边长
三角形面积
如图:圆锥的高是4cm,底面半径由小到大变化。
(2)如果圆锥底面半径为r(cm),那么圆锥的体积V(cm3)与r的关系为 。
(1)在这个变化过程中,自变量是_______________,因变量是_________
4cm
圆锥的底面半径
圆锥的体积
做一做
(3)当底面半径由1cm变化到10cm时,圆
锥的体积由 cm3变化到 cm3 。
4cm
如图:圆锥的高是4cm,底面半径由小到大变化。
做一做
(1)在这个变化过程中,自变量是 ,
因变量是 .
2㎝
(2)如果圆锥的高为h(cm),
那么圆锥的体积V(cm3)
与h之间的关系式为 .
(3)当高由1cm变化到10cm时,圆锥的体积
由 cm3变化到 cm3
圆锥的高
圆锥的体积
变式圆锥的底面半径2cm,高由小到大变化
(1)家居用电的二氧化碳排放量可以用关系式表示为 _______ ,
其中的字母表示什么?
y = 0.785x
y 为家居用电的二氧化碳排放量 ;
议一议
低碳生活
x 为耗电量 。
排碳计算公式
家居用电的二氧化碳排放量(kg)
=耗电量(kw?h)×0.785
开私家车的二氧化碳排放量(kg)
=油耗升数(L)×2.7
家用天然气的二氧化碳排放量(kg)
=天然气使用量(m3)×0.19
家用自来水的二气化碳排放量(kg)
=自来水吨数(t)×0.91
(2)在上述关系式中,耗电量每增加
1 KW·h,二氧化碳排放量增加_________。当耗电量从1 KW·h增加到100 KW·h时,二氧化碳排 放量从_______增加
到_________。
0.785kg
0.785kg
78.5kg
低碳生活
排碳计算公式
家居用电的二氧化碳排放量(kg)
=耗电量(kw?h)×0.785
开私家车的二氧化碳排放量(kg)
=油耗升数(L)×2.7
家用天然气的二氧化碳排放量(kg)
=天然气使用量(m3)×0.19
家用自来水的二气化碳排放量(kg)
=自来水吨数(t)×0.91
(3)小明家本月用电大约100 KW·h,天然气10m3,自来水10t,油耗10L,请你计算一下小明家这几项的二氧化碳排放量。
低碳生活
排碳计算公式
家居用电的二氧化碳排放量(kg)
=耗电量(kw?h)×0.785
开私家车的二氧化碳排放量(kg)
=油耗升数(L)×2.7
家用天然气的二氧化碳排放量(kg)
=天然气使用量(m3)×0.19
家用自来水的二气化碳排放量(kg)
=自来水吨数(t)×0.91
+
+
+
=
随堂练习
1、在地球某地,温度T(℃)与高度d
(m)的关系可以近似地用
来表示,根据这个关系式,当
d的值分别是200,400,600,
800,1000时,计算相应的T值,
并用表格表示所得结果
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x(cm)
0
200
400
600
800
1000
y(cm2)
10
10
8.67
7.33
6.00
4.67
3.33
2.某弹簧的自然长度为3cm,在弹性限度内所挂的物体的重量x 每增加1 kg ,弹簧长度y增加0.5cm。
x/kg
1
2
3
4
5
……
y/cm
……
(1)依据上表数据,写出y与x之间的关系式。
3.5
4
4.5
5
5.5
(2)当物体的质量为6kg时,根据(1)的关 系式求出弹簧的长度。
y = 3+0.5x
y = 3+0.5x6=9
燃烧时间x/分
10
20
30
40
50
…
剩余长度y/cm
19
18
17
16
15
…
3.一支原长为20cm的蜡烛,点燃后,其剩余
长度y(cm)与燃烧时间x(分)之间的关系如
下表:
则剩余长度y(cm)与燃烧时间x(分)关系式为 。 估计这支蜡烛最多可燃烧 分。
200
4、如图所示,梯形上底的长是a ,下底的长是15,
高是8,上底变化时,梯形的面积随之改变。
(1)梯形面积S与上底长a之间的关系式是什么?
a
8
15
(2)用表格表示当a从10变到15时(每次增加1),S的相应值;
(1) S=4a+60
a
10
11
12
13
14
15
S
100
104
108
112
116
120
a
8
15
(4)当a=0时,S等于什么?此时它表示的什么?
(3)当a每增加1时,S如何变化?
(3) a每增加1时,S增加4.
(4)a=0时,S=60,
此时它表示的是三角形的面积.
课后作业
课本
1.直接做在书上的作业:知识技能1、2。
2.做在作业本上的作业:数学理解3.
3.需要实际调查的作业:问题解决4(以报告单形式上交)
备用习题
1
2
3
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
