4.1.4 认识三角形及内角和三角形的高 课件(共30张PPT)
文档属性
| 名称 | 4.1.4 认识三角形及内角和三角形的高 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 20:54:44 | ||
图片预览




文档简介
数学北师大版
七年级下
4.1第4课时 认识三角形及内角和三角形的高
你还记得“过直线外一点画已知直线的垂线” 怎样画吗?
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画法
三角板的一条直角边与已知直线重合,另一条直角边过已知点
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
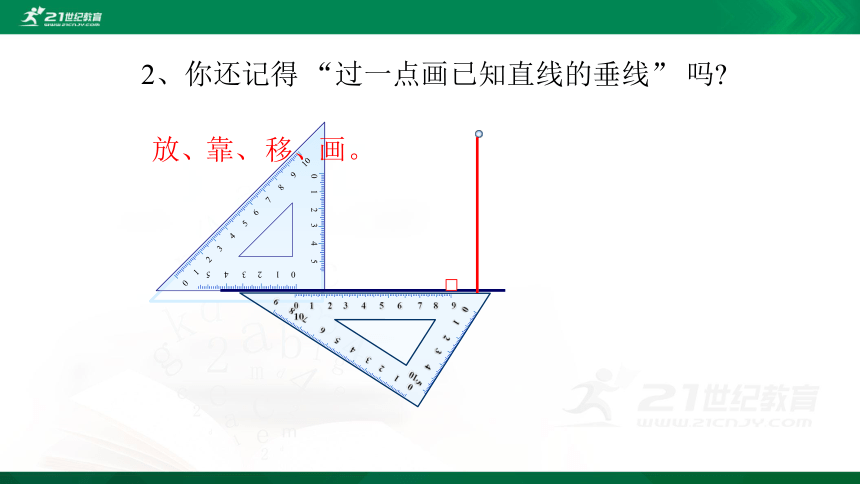
2、你还记得 “过一点画已知直线的垂线” 吗?
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
放、
靠、
移、
画。
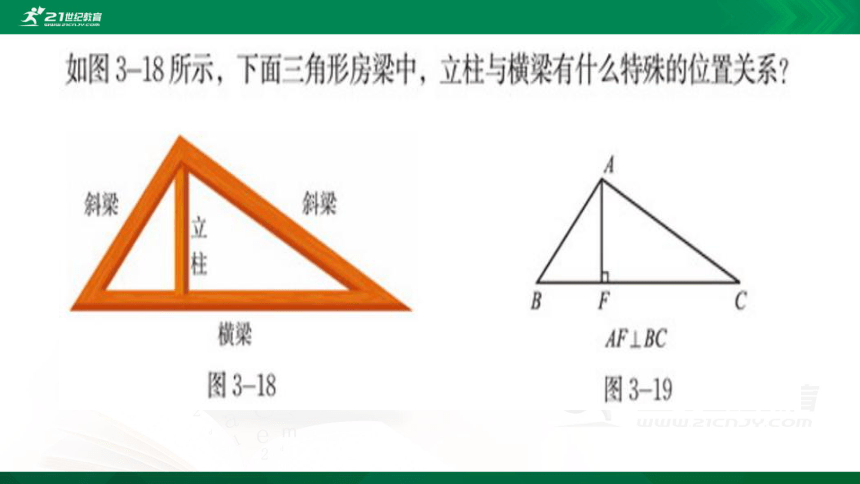
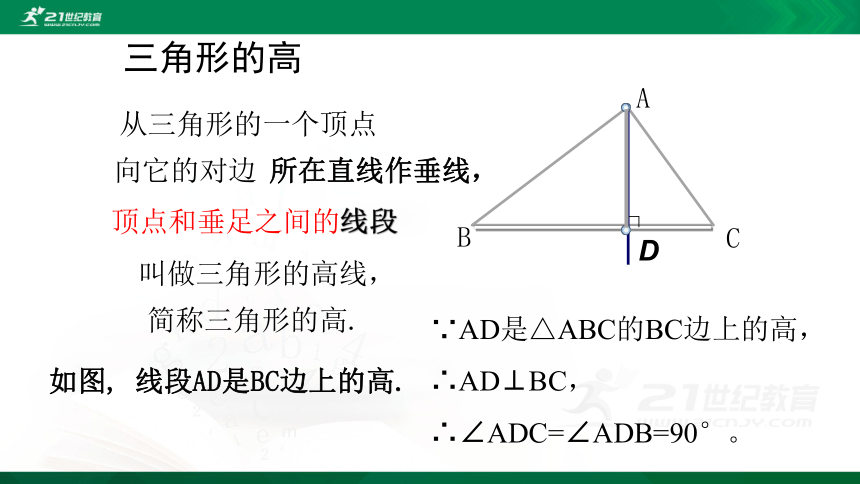
三角形的高
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点和垂足之间的线段
D
叫做三角形的高线,
简称三角形的高.
如图, 线段AD是BC边上的高.
∵AD是△ABC的BC边上的高,
∴AD⊥BC,
∴∠ADC=∠ADB=90°。
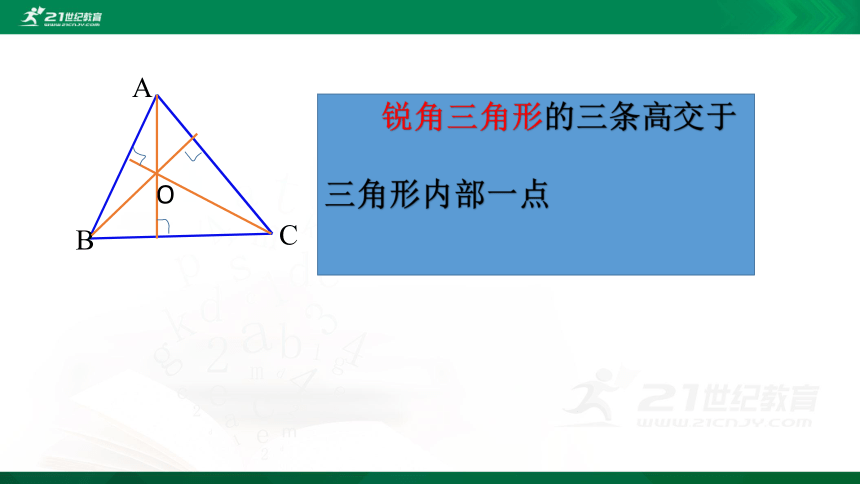
分类 活动一:做一做
拿出你准备好的锐角三角形纸片:
(1)你能画出这个三角形的三条高吗?
(2)你能用折纸的办法得到它们吗?
(3)这三条高之间有怎样的位置关系?
先独立思考、操作再小组交流.
注意:
使折痕过顶点,且这个顶点的对边边缘重合
C
B
A
O
锐角三角形的三条高交于
三角形内部一点
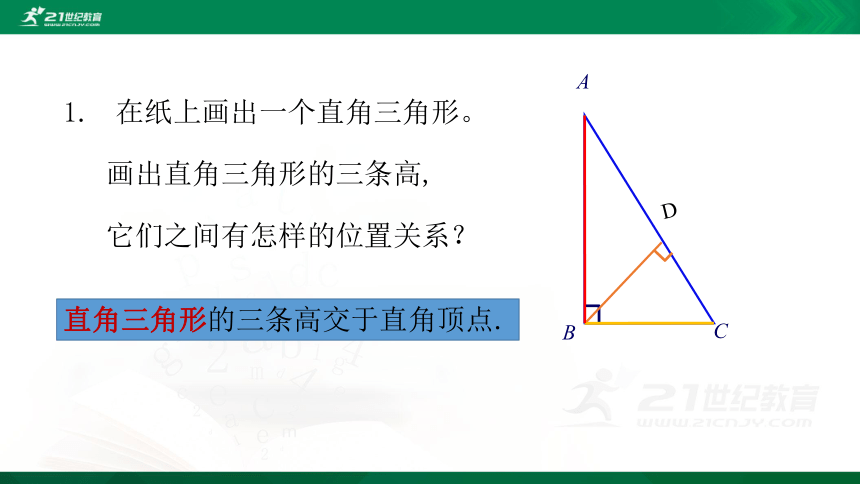
在纸上画出一个直角三角形。
画出直角三角形的三条高,
它们之间有怎样的位置关系?
A
B
C
D
直角三角形的三条高交于直角顶点.
2. 在纸上画出一个钝角三角形。
(1)你能折出钝角三角形的三条高吗?
(2)你能画出钝角三角形的三条高吗?
(3)钝角三角形的三条高交于一点吗?
它们所在的直线交于一点吗?
A
B
C
D
E
F
钝角三角形的三条高不交于一点
但它们所在的直线交于一点
画钝角三角形的三条高时,钝角的二边一定要延长
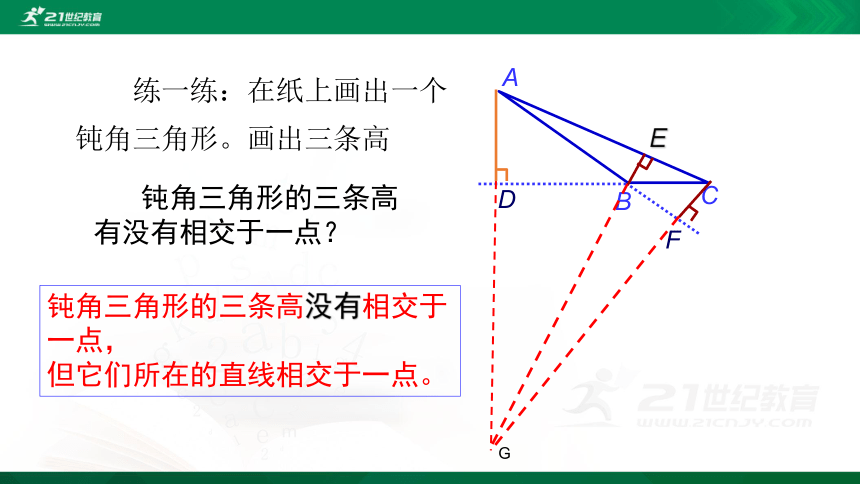
练一练:在纸上画出一个钝角三角形。画出三条高
E
A
B
C
D
F
G
钝角三角形的三条高有没有相交于一点?
钝角三角形的三条高没有相交于一点,
但它们所在的直线相交于一点。
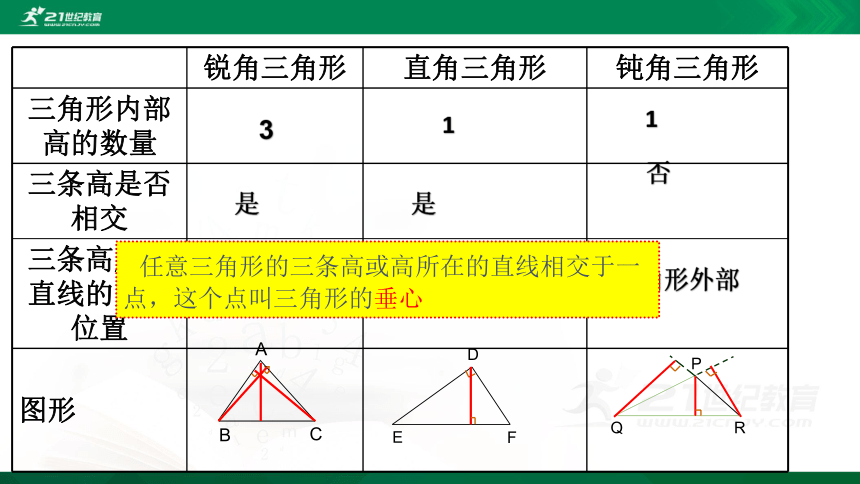
锐角三角形
直角三角形
钝角三角形
三角形内部高的数量
三条高是否相交
三条高所在直线的交点位置
图形
A
B
C
D
E
F
P
Q
R
3
1
1
是
是
否
三角形内部
直角顶点
三角形外部
任意三角形的三条高或高所在的直线相交于一点,这个点叫三角形的垂心
练一练:
A
B
C
A
B
C
C
B
A
AB边
CB边
BD
CE
AD
BF
D
E
D
F
CF
AD
BE
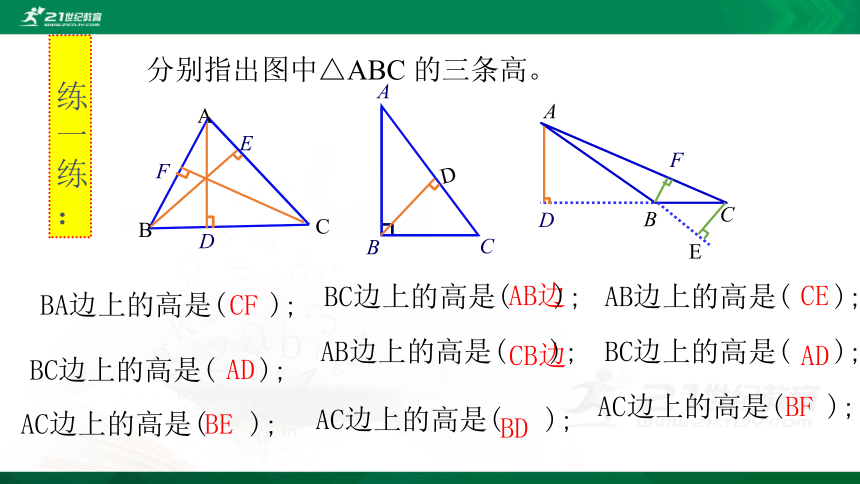
分别指出图中△ABC 的三条高。
D
F
E
BA边上的高是( );
AC边上的高是( );
BC边上的高是( );
BC边上的高是( );
BC边上的高是( );
AB边上的高是( );
AB边上的高是( );
AC边上的高是( );
AC边上的高是( );
如图,在△ABC中,BC边上的高是 ,AB边上的高是 ,
在 △BCE中,BE边上的高是 ,EC边上的高是 ,
在△ACD中,AC边上的高是 , CD边上的高是 。
A
F
C
B
D
E
AF
CE
CE
BE
AC
CD
说一说
1、不恢复这个缺角,请你画出AB边上的高所在的直线。
你是怎么画的?为什么?
2、在不恢复缺角的前提下,AB边上的高是否能画出?
一个缺角的三角形残片如图所示,
不能
问题解决
A
B
C
3.如图,∠ABC=∠ADC=∠FEC=90°.
(1)在△ABC中,BC边上的高是________;
(2)在△AEC中,AE边上的高是________;
(3)在△FEC中,EC边上的高是________;
(4)若AB=CD=3,AE=5,则△AEC的面积为________.
AB
DC
EF
7.5
4、如图1,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°,则∠A=_____.
5、如图2,已知∠ACB=90°,CD是斜边AB上的高线,可得:∠1=___,∠2=_____.(填写图中的角)
图1
图2
∠B
∠A
35°
锐角三角形
直角三角形
钝角三角形
三角形内部高的数量
三条高是否相交
三条高所在直线的交点位置
图形
A
B
C
D
E
F
P
Q
R
3
1
1
是
是
否
三角形内部
直角顶点
三角形外部
任意三角形的三条高或高所在的直线相交于一点,这个点叫三角形的垂心
本节知识点
1、如图,△ABC面积等于4,AD是△ABC的BC边上的中线,则△ABD的面积等于___ ;
DE是△ADC的AC边上的中线,则△ADE的面积等于_____ 。
2
1
思考:三角形的一条中线分成的两个三角形面积有什么关系?
课外作业
相等并等于原三角形的面积一半
2.如图,0是△ABC的重心,则图中与△ABD面积相等的三角形个数为( )
3.如图,△ABC中,AD为中线,DE⊥AB于点E,DF⊥AC于点F,AB=3,AC=4,DF=1.5,求DE的长.
4.如图,在△ABC中, ∠ABC=∠C,∠A=36° ,BD是△ABC的角平分线,BE⊥AC, 求∠ADB、∠DBE的度数.
5.在△ABC中,已知D、E、F分别为BC、AD、CE的中点.(1)如图①,若S△ABC = 1cm2求△BEF的面积;
(2)如图②,若S△BFC=1,求S△ABC
6、如图,在△ABC中,AD平分∠BAC,AE⊥BC于点E。若∠B=300,∠C=500,求∠DAE的度数。
A
B
C
D
E
解:∵∠B=300,∠C=500
∴∠BAC=1800-∠B-∠C =1800-300-500=1000
∵AD平分∠BAC
∴∠DAC= ∠BAC=500
∵AE⊥BC
∴∠AEC=900
∴∠CAE=900-∠C=900-500=400
∴∠DAE=∠DAC-∠CAE=500-400=100
7.如图,在△ABC中BD⊥AC于D,CE⊥AB于E,
(1)猜测∠1与∠2的关系,并说明理由。
(2)如果∠BAC是钝角,(1)中的结论是否成立?并说明理由。
A
B
C
D
E
1
2
解:∠1=∠2,理由如下:
∵ BD⊥AC,CE⊥AB
∴在Rt△ADB和Rt△BDC中
∠2+ ∠A=900, ∠1+ ∠A=900
∴ ∠1=∠2
(2)如果∠BAC是钝角,(1)中的结论是否成立?并说明理由。
A
B
C
D
E
1
2
解:(1)中的结论仍然成立
∵ BD⊥AC,CE⊥AB
∴在Rt△ADB和Rt△BDC中
∠2+∠3=900, ∠1+∠4=900
∵ ∠3=∠4
∴ ∠1=∠2
∴ (1)中的结论仍然成立
3
4
8.已知△ABC三边之比AB: BC: AC=3 : 4: 5,则AB,BC,AC边上的高之比为( C)
A.5:4:3 B.3:4:5 C.20: 15 : 12
D.20: 15 : 9
9.如图,在△ABC中,AB=AC=8,P是BC上任意一点,PD⊥AB于点D,PE⊥AC于点E.若△ABC的面积为14,问:PD+PE的值是否确定?若能确定,则PD+PE的值是多少?若不能确定,请说明理由.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
七年级下
4.1第4课时 认识三角形及内角和三角形的高
你还记得“过直线外一点画已知直线的垂线” 怎样画吗?
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画法
三角板的一条直角边与已知直线重合,另一条直角边过已知点
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
2、你还记得 “过一点画已知直线的垂线” 吗?
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
放、
靠、
移、
画。
三角形的高
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点和垂足之间的线段
D
叫做三角形的高线,
简称三角形的高.
如图, 线段AD是BC边上的高.
∵AD是△ABC的BC边上的高,
∴AD⊥BC,
∴∠ADC=∠ADB=90°。
分类 活动一:做一做
拿出你准备好的锐角三角形纸片:
(1)你能画出这个三角形的三条高吗?
(2)你能用折纸的办法得到它们吗?
(3)这三条高之间有怎样的位置关系?
先独立思考、操作再小组交流.
注意:
使折痕过顶点,且这个顶点的对边边缘重合
C
B
A
O
锐角三角形的三条高交于
三角形内部一点
在纸上画出一个直角三角形。
画出直角三角形的三条高,
它们之间有怎样的位置关系?
A
B
C
D
直角三角形的三条高交于直角顶点.
2. 在纸上画出一个钝角三角形。
(1)你能折出钝角三角形的三条高吗?
(2)你能画出钝角三角形的三条高吗?
(3)钝角三角形的三条高交于一点吗?
它们所在的直线交于一点吗?
A
B
C
D
E
F
钝角三角形的三条高不交于一点
但它们所在的直线交于一点
画钝角三角形的三条高时,钝角的二边一定要延长
练一练:在纸上画出一个钝角三角形。画出三条高
E
A
B
C
D
F
G
钝角三角形的三条高有没有相交于一点?
钝角三角形的三条高没有相交于一点,
但它们所在的直线相交于一点。
锐角三角形
直角三角形
钝角三角形
三角形内部高的数量
三条高是否相交
三条高所在直线的交点位置
图形
A
B
C
D
E
F
P
Q
R
3
1
1
是
是
否
三角形内部
直角顶点
三角形外部
任意三角形的三条高或高所在的直线相交于一点,这个点叫三角形的垂心
练一练:
A
B
C
A
B
C
C
B
A
AB边
CB边
BD
CE
AD
BF
D
E
D
F
CF
AD
BE
分别指出图中△ABC 的三条高。
D
F
E
BA边上的高是( );
AC边上的高是( );
BC边上的高是( );
BC边上的高是( );
BC边上的高是( );
AB边上的高是( );
AB边上的高是( );
AC边上的高是( );
AC边上的高是( );
如图,在△ABC中,BC边上的高是 ,AB边上的高是 ,
在 △BCE中,BE边上的高是 ,EC边上的高是 ,
在△ACD中,AC边上的高是 , CD边上的高是 。
A
F
C
B
D
E
AF
CE
CE
BE
AC
CD
说一说
1、不恢复这个缺角,请你画出AB边上的高所在的直线。
你是怎么画的?为什么?
2、在不恢复缺角的前提下,AB边上的高是否能画出?
一个缺角的三角形残片如图所示,
不能
问题解决
A
B
C
3.如图,∠ABC=∠ADC=∠FEC=90°.
(1)在△ABC中,BC边上的高是________;
(2)在△AEC中,AE边上的高是________;
(3)在△FEC中,EC边上的高是________;
(4)若AB=CD=3,AE=5,则△AEC的面积为________.
AB
DC
EF
7.5
4、如图1,在直角△ABC中,CD是斜边AB上的高,∠BCD=35°,则∠A=_____.
5、如图2,已知∠ACB=90°,CD是斜边AB上的高线,可得:∠1=___,∠2=_____.(填写图中的角)
图1
图2
∠B
∠A
35°
锐角三角形
直角三角形
钝角三角形
三角形内部高的数量
三条高是否相交
三条高所在直线的交点位置
图形
A
B
C
D
E
F
P
Q
R
3
1
1
是
是
否
三角形内部
直角顶点
三角形外部
任意三角形的三条高或高所在的直线相交于一点,这个点叫三角形的垂心
本节知识点
1、如图,△ABC面积等于4,AD是△ABC的BC边上的中线,则△ABD的面积等于___ ;
DE是△ADC的AC边上的中线,则△ADE的面积等于_____ 。
2
1
思考:三角形的一条中线分成的两个三角形面积有什么关系?
课外作业
相等并等于原三角形的面积一半
2.如图,0是△ABC的重心,则图中与△ABD面积相等的三角形个数为( )
3.如图,△ABC中,AD为中线,DE⊥AB于点E,DF⊥AC于点F,AB=3,AC=4,DF=1.5,求DE的长.
4.如图,在△ABC中, ∠ABC=∠C,∠A=36° ,BD是△ABC的角平分线,BE⊥AC, 求∠ADB、∠DBE的度数.
5.在△ABC中,已知D、E、F分别为BC、AD、CE的中点.(1)如图①,若S△ABC = 1cm2求△BEF的面积;
(2)如图②,若S△BFC=1,求S△ABC
6、如图,在△ABC中,AD平分∠BAC,AE⊥BC于点E。若∠B=300,∠C=500,求∠DAE的度数。
A
B
C
D
E
解:∵∠B=300,∠C=500
∴∠BAC=1800-∠B-∠C =1800-300-500=1000
∵AD平分∠BAC
∴∠DAC= ∠BAC=500
∵AE⊥BC
∴∠AEC=900
∴∠CAE=900-∠C=900-500=400
∴∠DAE=∠DAC-∠CAE=500-400=100
7.如图,在△ABC中BD⊥AC于D,CE⊥AB于E,
(1)猜测∠1与∠2的关系,并说明理由。
(2)如果∠BAC是钝角,(1)中的结论是否成立?并说明理由。
A
B
C
D
E
1
2
解:∠1=∠2,理由如下:
∵ BD⊥AC,CE⊥AB
∴在Rt△ADB和Rt△BDC中
∠2+ ∠A=900, ∠1+ ∠A=900
∴ ∠1=∠2
(2)如果∠BAC是钝角,(1)中的结论是否成立?并说明理由。
A
B
C
D
E
1
2
解:(1)中的结论仍然成立
∵ BD⊥AC,CE⊥AB
∴在Rt△ADB和Rt△BDC中
∠2+∠3=900, ∠1+∠4=900
∵ ∠3=∠4
∴ ∠1=∠2
∴ (1)中的结论仍然成立
3
4
8.已知△ABC三边之比AB: BC: AC=3 : 4: 5,则AB,BC,AC边上的高之比为( C)
A.5:4:3 B.3:4:5 C.20: 15 : 12
D.20: 15 : 9
9.如图,在△ABC中,AB=AC=8,P是BC上任意一点,PD⊥AB于点D,PE⊥AC于点E.若△ABC的面积为14,问:PD+PE的值是否确定?若能确定,则PD+PE的值是多少?若不能确定,请说明理由.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
