4.2 图形的全等 课件(共33张PPT)
文档属性
| 名称 | 4.2 图形的全等 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 20:56:50 | ||
图片预览



文档简介
数学北师大版
七年级下
4.2 图形的全等
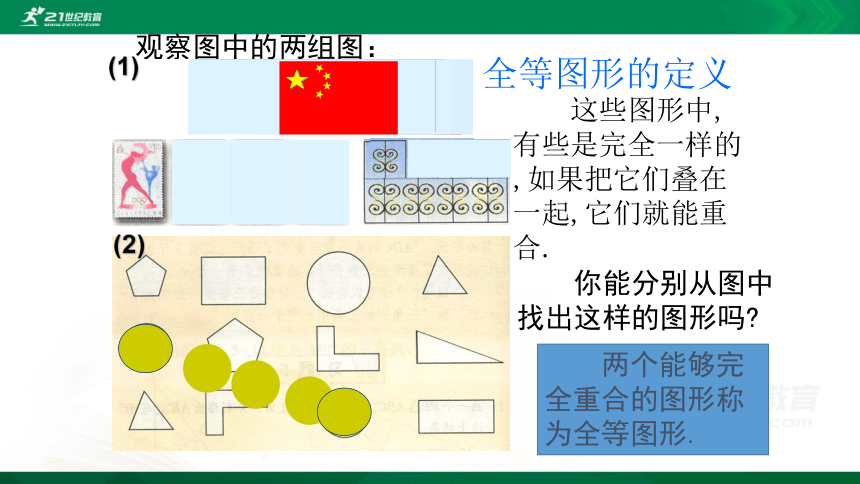
观察图中的两组图:
(1)
(2)
这些图形中,有些是完全一样的,如果把它们叠在一起,它们就能重合.
你能分别从图中找出这样的图形吗?
两个能够完全重合的图形称为全等图形.
全等图形的定义
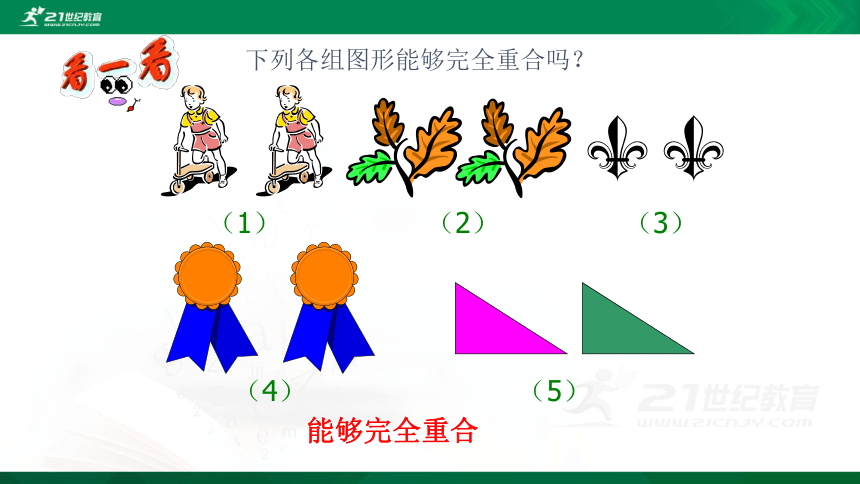
下列各组图形能够完全重合吗?
(1)
(4)
(3)
(2)
(5)
能够完全重合
1、你能列举生活中全等图形的例子吗?
议一议
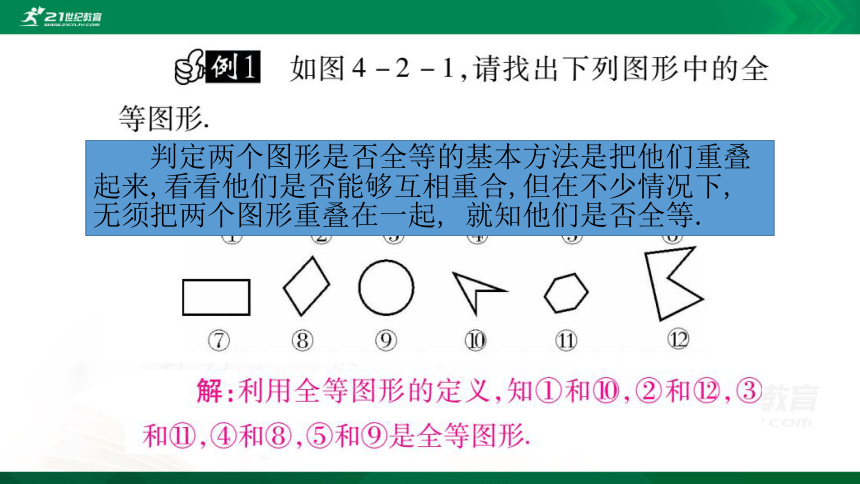
判定两个图形是否全等的基本方法是把他们重叠起来,看看他们是否能够互相重合,但在不少情况下, 无须把两个图形重叠在一起, 就知他们是否全等.
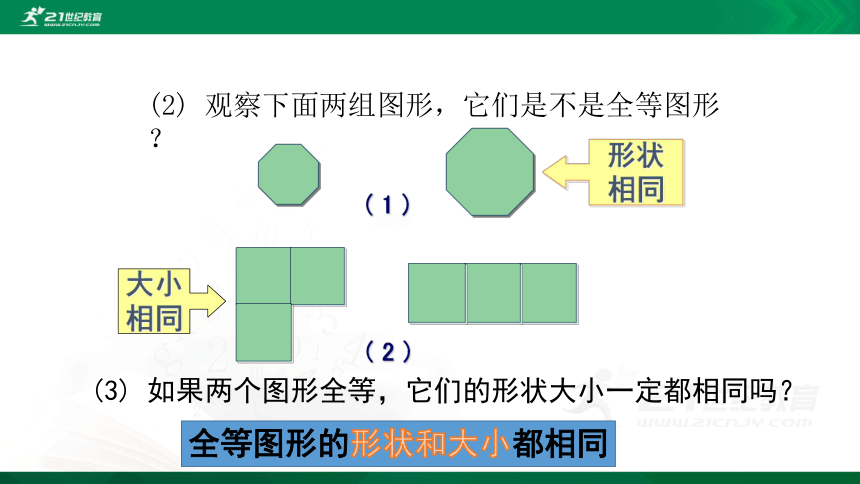
全等图形的形状和大小都相同
形状
相同
大小
相同
(2) 观察下面两组图形,它们是不是全等图形?
( 1 )
( 2 )
(3) 如果两个图形全等,它们的形状大小一定都相同吗?
D
E
F
A
B
C
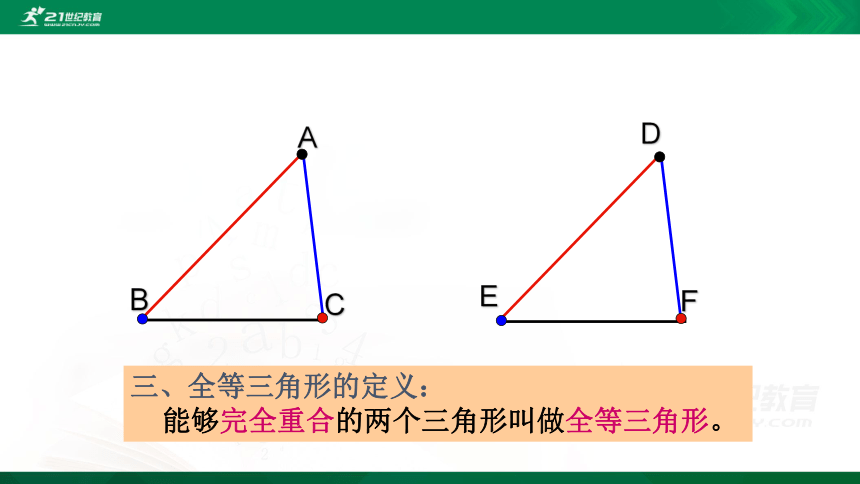
三、全等三角形的定义:
能够完全重合的两个三角形叫做全等三角形。
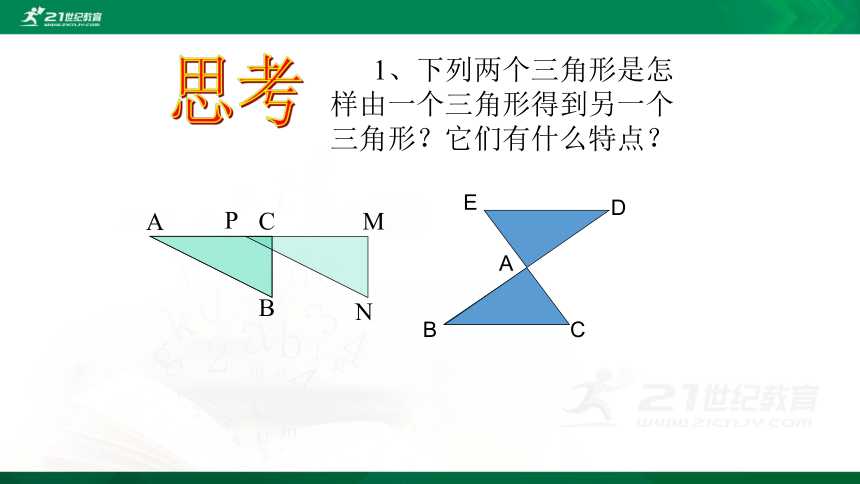
1、下列两个三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?
思考
B
A
C
N
P
M
A
C
B
D
E
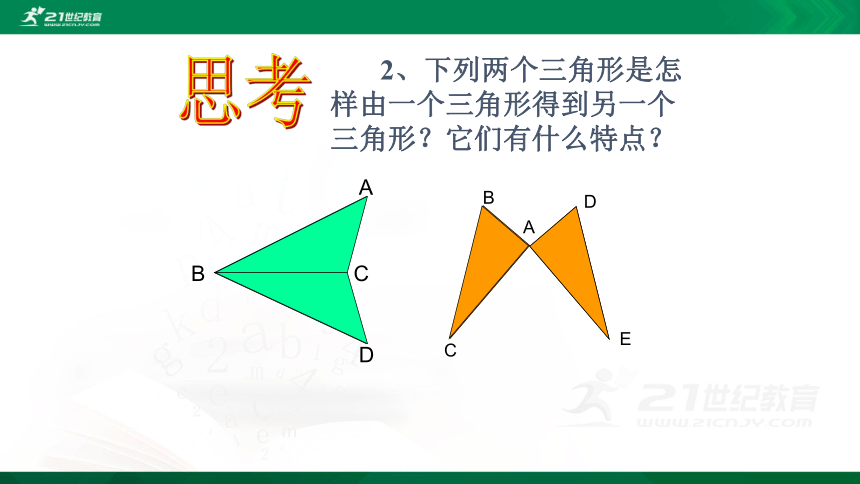
2、下列两个三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?
思考
A
B
C
D
C
B
A
D
E
A
B
C
A1
B1
C1
对应顶点:点A和点A1,点B和点B1,点C和点C1,
全等三角形的对应元素:
对应边:AB和 A1B1,AC 和 A1C1,BC和B1C1
对应角:∠A 和∠A1, ∠B 和 ∠B1, ∠C 和 ∠C1
全等三角形的对应边相等,对应角相等。
想一想
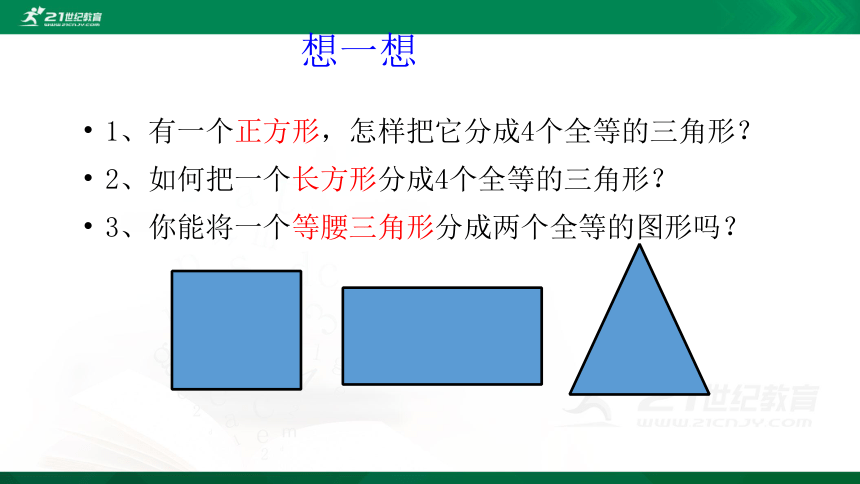
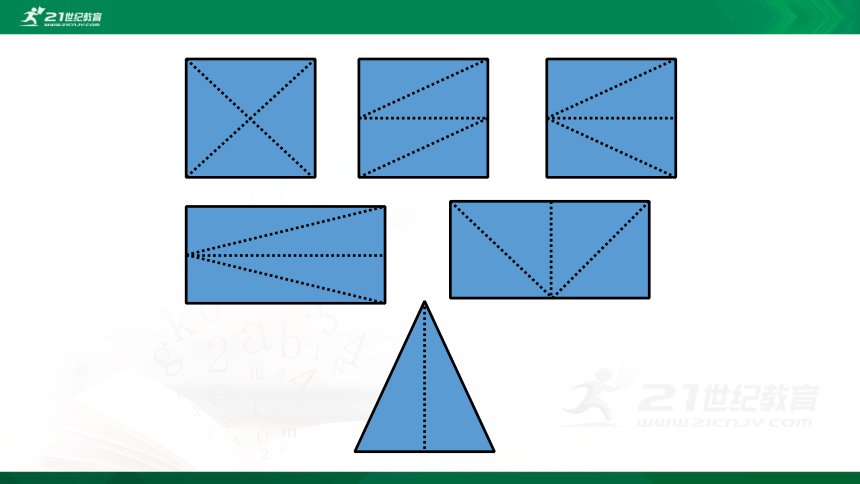
1、有一个正方形,怎样把它分成4个全等的三角形?
2、如何把一个长方形分成4个全等的三角形?
3、你能将一个等腰三角形分成两个全等的图形吗?
D
E
F
A
B
C
如图:△ABC 与△DEF全等
记作: △ABC ≌ △DEF
读作: △ABC 全等于 △DEF
“全等”符号“≌”,读作“全等于”
五:全等三角形的表示
两个三角形全等在表示时通常把对应顶点的字母写在对应的位置上。
全等三角形的对应边相等,全等三角形的对应角相等.
如图:∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE
∵△ABC≌ △DFE
∴∠A=∠D,∠B=∠F,∠C=∠E
D
E
F
A
B
C
几何语言:
全等三角形的性质
A
B
C
E
D
F
全等三角形的表示
你能否直接从记作?ABC≌ ?DEF中判断出所有的对应顶点、对应边和对应角?
AB=DF, BC=FE, AC=DE
∠A=∠D,∠B=∠F,∠C=∠E
方法对应位置的字母相对应为.
点A与点D,点B与点E,点C与点F
能:
全等三角形对应边上高相等,
对应角平分线相等,
对应边上的中线也相等(简称三角形的三线)
全等三角形的性质
全等三角形的对应边相等,全等三角形的对应角相等.
全等三角形的周长相等,面积也相等
例1、如图△ABC≌△DCB,
指出所有的对应边与对应角。
O
D
C
B
A
解:∵△ABC≌△DCB
∴AB与DC,BC与CB,AC与BD是对应边
∠A与∠ D,∠ABC与∠DCB,
∠ACB与∠DBC是对应角
规律:一对最长的边是对应边
一对最短的边是对应边
规律:一对最大的角是对应角
一对最小的角是对应角
练习:1.(1)如图△ABC≌△DCB,
指出所有的对应边与对应角。
A
C
D
B
解:∵△AOC≌△BOD
∴AO=BO,AC=BD,OC=OD.
∴∠A=∠B,∠C=∠D,
∠AOC= ∠BOD.
有对顶角的,对顶角是对应角
o
2、 先写出全等式,再指出它们的对应边和对应角。
下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?试试看?
做一做
巩固练习:
1.如图,已知△ABC ≌ △AEC,∠B=30°, ∠ACB=85°,求出 △AEC各内角的度数.
30°
85°
65°
30°
65°
85°
1.全等图形.
(1)全等图形的定义:能够_________的两个图形称为全等图形.
(2)全等图形的判别:形状_____,大小_____时,才能称为全等
图形.
【点拨】全等图形的判别只与两个图形的形状和大小有关,与
图形的位置和方向无关.
(3)全等图形的性质:全等图形的_____和_____都相同.
完全重合
相同
相同
形状
大小
课堂小结
2.全等三角形.
(1)定义:能够_________的两个三角形叫做全等三角形.
(2)对应元素:两个三角形全等时,重合的顶点是_______,重
合的边是_______,重合的角是_______.
(3)表示:全等三角形用符号:≌表示,读作:_______.
注意:在表示两个三角形全等时,通常要把对应顶点的_____写
在对应的位置上.
(4)性质:全等三角形的对应边_____,对应角_____,对应边上
的高、中线、角平分线也_____,对应周长、面积也_____.
归纳:全等三角形的一切对应元素都_____.
完全重合
对应点
对应边
对应角
全等于
字母
相等
相等
相等
相等
相等
3、全等三角形找对应边、对应角的规律与方法:
(1)有公共边的,公共边一定是对应边,
有对顶角或公共角的,对顶角或公共角一定是对应角;
(2)对应角所对的边是对应边,对应边所对的角是对应角;
(3)最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角;
作业:
习题:4.5
1、2、3、4、5
课外作业:
1.如图:⊿ADC≌⊿BFE,
∠E=∠C,AB=7,
DF=3,求AF的长?
A
B
C
E
F
D
解:
∵⊿ADC≌⊿BFE,∠E=∠C
∴AD=BF
∴AD-DF=BF-DF
即AF=BD
又∵ AF+BD=AB-DF=7-3=4(cm)
∴AF=BD=2cm
2.如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB的度数.
【规范解答】因为△ABC≌△ADE,
所以∠DAE=∠BAC.
又因为∠EAB=120°,∠CAD=10°,
所以∠BAC= (∠EAB-∠CAD)= (120°-10°)=55°,
所以∠DAB=∠CAD+∠BAC=10°+55°=65°.又因为在△ABF中,∠B=25°,
所以∠AFB=180°-∠B-∠BAF=180°-25°-65°=90°,
所以∠DFB=180°-∠AFB=90°.
3.如图,△ACB≌△A′CB′,∠B′CB=30°,则∠ACA′的度数为( )
(A)20° (B)30° (C)35° (D)40°
【解析】选B.因为△ACB≌△A′CB′,所以∠ACB=∠A′CB′,即∠ACA′+∠A′CB=∠B′CB+∠A′CB,
所以∠ACA′=∠B′CB.又∠B′CB=30°,
所以∠ACA′=30°.
【变式备选】如图,D,E是△ABC的边AC,
BC上的点,△ADB≌△EDB≌△EDC.下列
结论:①AD=ED;②BC=2AB;③∠1=∠2
=∠3;④∠4=∠5=∠6.其中正确的有( )
(A)4个 (B)3个 (C)2个 (D)1个
A
【解析】选A.因为△ADB≌△EDB,所以AD=ED,AB=EB,∠1=∠2,∠4=∠5.因为△EDB≌△EDC,所以BE=CE,∠2=∠3,∠5=∠6,所以∠1=∠2=∠3,∠4=∠5=∠6,BC=2BE,又AB=BE,所以BC=2AB.所以4个结论均正确.
4.如图△ABC≌△DEF,∠A=25°,∠B=65° , BF =3cm,求∠DFE的度数和EC的长.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
七年级下
4.2 图形的全等
观察图中的两组图:
(1)
(2)
这些图形中,有些是完全一样的,如果把它们叠在一起,它们就能重合.
你能分别从图中找出这样的图形吗?
两个能够完全重合的图形称为全等图形.
全等图形的定义
下列各组图形能够完全重合吗?
(1)
(4)
(3)
(2)
(5)
能够完全重合
1、你能列举生活中全等图形的例子吗?
议一议
判定两个图形是否全等的基本方法是把他们重叠起来,看看他们是否能够互相重合,但在不少情况下, 无须把两个图形重叠在一起, 就知他们是否全等.
全等图形的形状和大小都相同
形状
相同
大小
相同
(2) 观察下面两组图形,它们是不是全等图形?
( 1 )
( 2 )
(3) 如果两个图形全等,它们的形状大小一定都相同吗?
D
E
F
A
B
C
三、全等三角形的定义:
能够完全重合的两个三角形叫做全等三角形。
1、下列两个三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?
思考
B
A
C
N
P
M
A
C
B
D
E
2、下列两个三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?
思考
A
B
C
D
C
B
A
D
E
A
B
C
A1
B1
C1
对应顶点:点A和点A1,点B和点B1,点C和点C1,
全等三角形的对应元素:
对应边:AB和 A1B1,AC 和 A1C1,BC和B1C1
对应角:∠A 和∠A1, ∠B 和 ∠B1, ∠C 和 ∠C1
全等三角形的对应边相等,对应角相等。
想一想
1、有一个正方形,怎样把它分成4个全等的三角形?
2、如何把一个长方形分成4个全等的三角形?
3、你能将一个等腰三角形分成两个全等的图形吗?
D
E
F
A
B
C
如图:△ABC 与△DEF全等
记作: △ABC ≌ △DEF
读作: △ABC 全等于 △DEF
“全等”符号“≌”,读作“全等于”
五:全等三角形的表示
两个三角形全等在表示时通常把对应顶点的字母写在对应的位置上。
全等三角形的对应边相等,全等三角形的对应角相等.
如图:∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE
∵△ABC≌ △DFE
∴∠A=∠D,∠B=∠F,∠C=∠E
D
E
F
A
B
C
几何语言:
全等三角形的性质
A
B
C
E
D
F
全等三角形的表示
你能否直接从记作?ABC≌ ?DEF中判断出所有的对应顶点、对应边和对应角?
AB=DF, BC=FE, AC=DE
∠A=∠D,∠B=∠F,∠C=∠E
方法对应位置的字母相对应为.
点A与点D,点B与点E,点C与点F
能:
全等三角形对应边上高相等,
对应角平分线相等,
对应边上的中线也相等(简称三角形的三线)
全等三角形的性质
全等三角形的对应边相等,全等三角形的对应角相等.
全等三角形的周长相等,面积也相等
例1、如图△ABC≌△DCB,
指出所有的对应边与对应角。
O
D
C
B
A
解:∵△ABC≌△DCB
∴AB与DC,BC与CB,AC与BD是对应边
∠A与∠ D,∠ABC与∠DCB,
∠ACB与∠DBC是对应角
规律:一对最长的边是对应边
一对最短的边是对应边
规律:一对最大的角是对应角
一对最小的角是对应角
练习:1.(1)如图△ABC≌△DCB,
指出所有的对应边与对应角。
A
C
D
B
解:∵△AOC≌△BOD
∴AO=BO,AC=BD,OC=OD.
∴∠A=∠B,∠C=∠D,
∠AOC= ∠BOD.
有对顶角的,对顶角是对应角
o
2、 先写出全等式,再指出它们的对应边和对应角。
下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?试试看?
做一做
巩固练习:
1.如图,已知△ABC ≌ △AEC,∠B=30°, ∠ACB=85°,求出 △AEC各内角的度数.
30°
85°
65°
30°
65°
85°
1.全等图形.
(1)全等图形的定义:能够_________的两个图形称为全等图形.
(2)全等图形的判别:形状_____,大小_____时,才能称为全等
图形.
【点拨】全等图形的判别只与两个图形的形状和大小有关,与
图形的位置和方向无关.
(3)全等图形的性质:全等图形的_____和_____都相同.
完全重合
相同
相同
形状
大小
课堂小结
2.全等三角形.
(1)定义:能够_________的两个三角形叫做全等三角形.
(2)对应元素:两个三角形全等时,重合的顶点是_______,重
合的边是_______,重合的角是_______.
(3)表示:全等三角形用符号:≌表示,读作:_______.
注意:在表示两个三角形全等时,通常要把对应顶点的_____写
在对应的位置上.
(4)性质:全等三角形的对应边_____,对应角_____,对应边上
的高、中线、角平分线也_____,对应周长、面积也_____.
归纳:全等三角形的一切对应元素都_____.
完全重合
对应点
对应边
对应角
全等于
字母
相等
相等
相等
相等
相等
3、全等三角形找对应边、对应角的规律与方法:
(1)有公共边的,公共边一定是对应边,
有对顶角或公共角的,对顶角或公共角一定是对应角;
(2)对应角所对的边是对应边,对应边所对的角是对应角;
(3)最大边与最大边(最小边与最小边)为对应边;
最大角与最大角(最小角与最小角)为对应角;
作业:
习题:4.5
1、2、3、4、5
课外作业:
1.如图:⊿ADC≌⊿BFE,
∠E=∠C,AB=7,
DF=3,求AF的长?
A
B
C
E
F
D
解:
∵⊿ADC≌⊿BFE,∠E=∠C
∴AD=BF
∴AD-DF=BF-DF
即AF=BD
又∵ AF+BD=AB-DF=7-3=4(cm)
∴AF=BD=2cm
2.如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB的度数.
【规范解答】因为△ABC≌△ADE,
所以∠DAE=∠BAC.
又因为∠EAB=120°,∠CAD=10°,
所以∠BAC= (∠EAB-∠CAD)= (120°-10°)=55°,
所以∠DAB=∠CAD+∠BAC=10°+55°=65°.又因为在△ABF中,∠B=25°,
所以∠AFB=180°-∠B-∠BAF=180°-25°-65°=90°,
所以∠DFB=180°-∠AFB=90°.
3.如图,△ACB≌△A′CB′,∠B′CB=30°,则∠ACA′的度数为( )
(A)20° (B)30° (C)35° (D)40°
【解析】选B.因为△ACB≌△A′CB′,所以∠ACB=∠A′CB′,即∠ACA′+∠A′CB=∠B′CB+∠A′CB,
所以∠ACA′=∠B′CB.又∠B′CB=30°,
所以∠ACA′=30°.
【变式备选】如图,D,E是△ABC的边AC,
BC上的点,△ADB≌△EDB≌△EDC.下列
结论:①AD=ED;②BC=2AB;③∠1=∠2
=∠3;④∠4=∠5=∠6.其中正确的有( )
(A)4个 (B)3个 (C)2个 (D)1个
A
【解析】选A.因为△ADB≌△EDB,所以AD=ED,AB=EB,∠1=∠2,∠4=∠5.因为△EDB≌△EDC,所以BE=CE,∠2=∠3,∠5=∠6,所以∠1=∠2=∠3,∠4=∠5=∠6,BC=2BE,又AB=BE,所以BC=2AB.所以4个结论均正确.
4.如图△ABC≌△DEF,∠A=25°,∠B=65° , BF =3cm,求∠DFE的度数和EC的长.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
