4.3.2 全等三角形的判定 课件(共27张PPT)
文档属性
| 名称 | 4.3.2 全等三角形的判定 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 21:09:40 | ||
图片预览


文档简介
数学北师大版
七年级下
4.3全等三角形的判定
角边角与角角边(第2课时)
①三角;
②三边;
④两边一角;
③两角一边。
如果满足三个条件,画出的三角形一定全等吗?
探索三角形全等的条件
③两角一边。
1.有角边角(ASA) 和 2.角角边(AAS)这二种情况
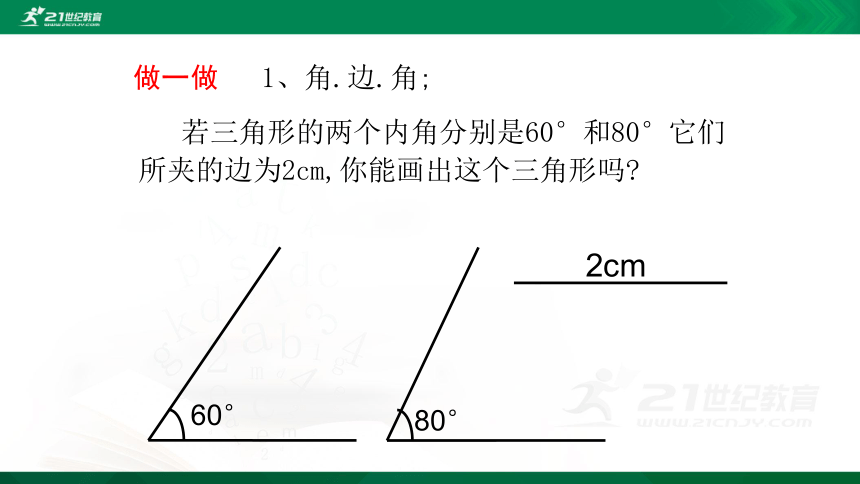
做一做
1、角.边.角;
若三角形的两个内角分别是60°和80°它们所夹的边为2cm,你能画出这个三角形吗?
2cm
60°
80°
60°
80°
2cm
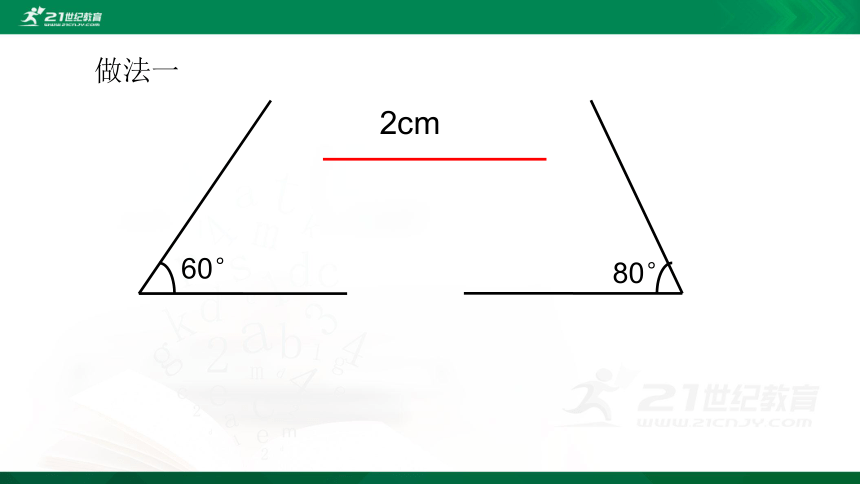
做法一
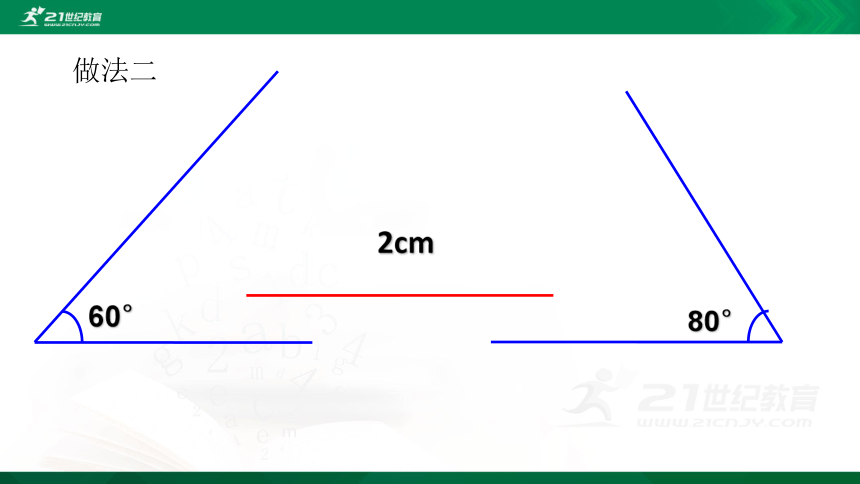
60°
80°
2cm
做法二
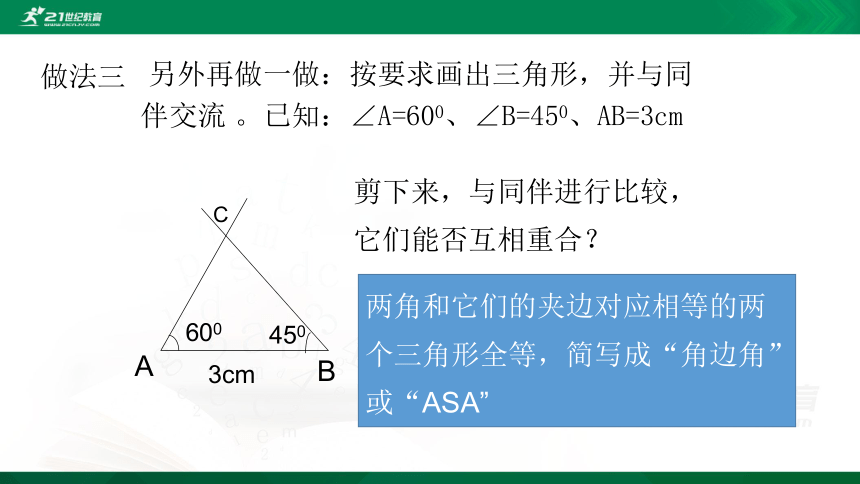
另外再做一做:按要求画出三角形,并与同伴交流 。已知:∠A=600、∠B=450、AB=3cm
A
B
C
600
450
3cm
两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”
剪下来,与同伴进行比较,它们能否互相重合?
做法三
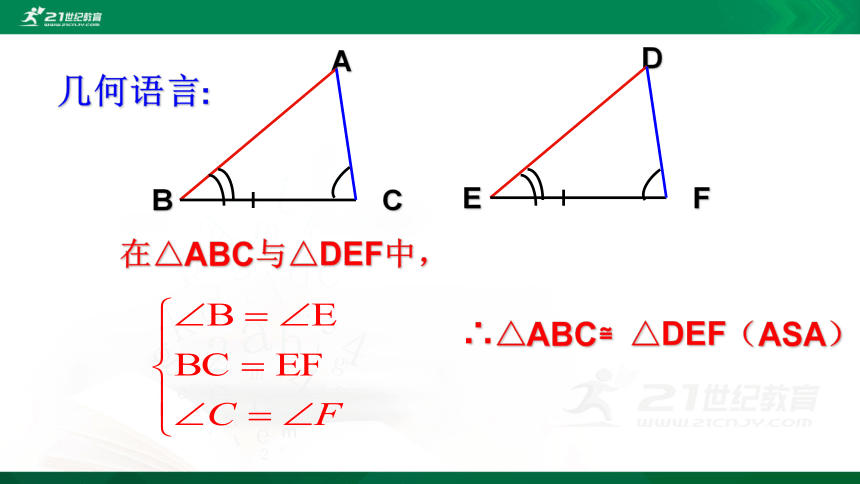
在△ABC与△DEF中,
∴△ABC≌△DEF(ASA)
几何语言:
A
B
C
D
E
F
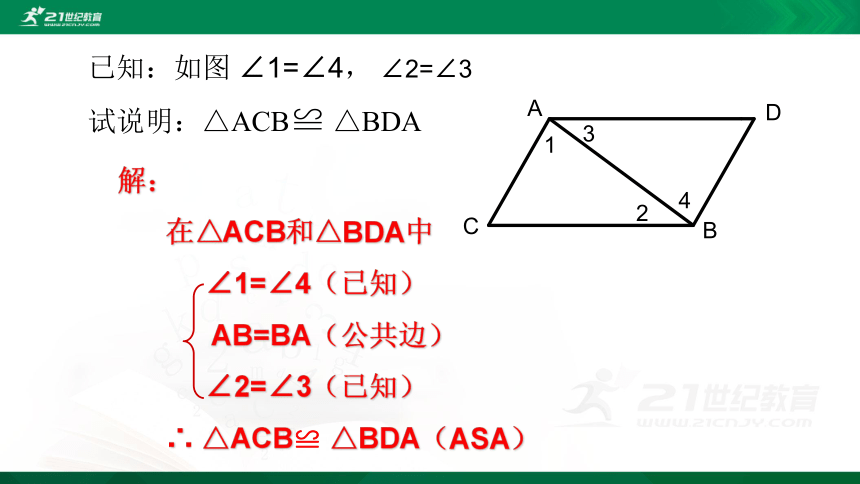
已知:如图 ∠1=∠4, ∠2=∠3
试说明:△ACB≌ △BDA
解:
在△ACB和△BDA中
∠1=∠4(已知)
AB=BA(公共边)
∠2=∠3(已知)
∴ △ACB≌ △BDA(ASA)
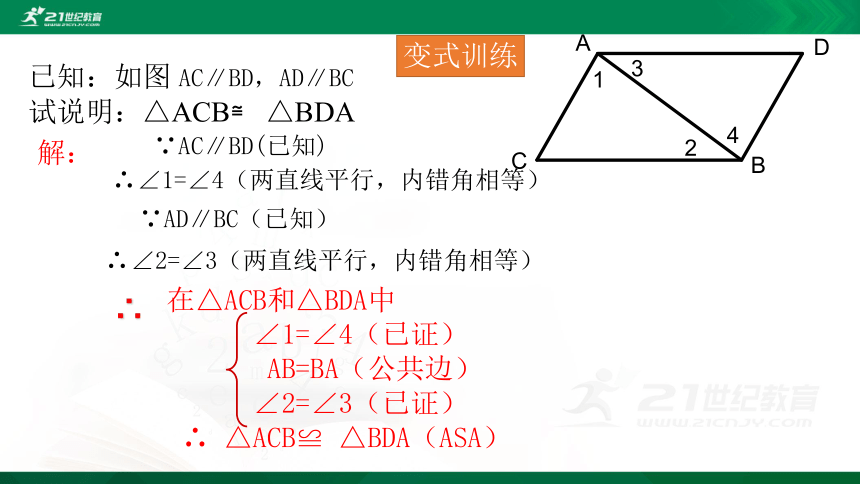
已知:如图 AC∥BD,AD∥BC
试说明:△ACB≌ △BDA
在△ACB和△BDA中
∠1=∠4(已证)
AB=BA(公共边)
∠2=∠3(已证)
∴ △ACB≌ △BDA(ASA)
∴∠2=∠3(两直线平行,内错角相等)
∵AC∥BD(已知)
∴∠1=∠4(两直线平行,内错角相等)
∵AD∥BC(已知)
∴
解:
变式训练
如图,O是AB的中点,∠A=∠B,△AOC与△BOD全等吗?为什么?
A
B
C
D
O
△AOC △BOD
∠A=∠B
≌
AO=OB
∠AOC=∠BOD
(已知)
(中点定义)
(对顶角相等)
(ASA)
解:全等。理由如下
2、角.角.边
若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗?
60°
45°
已知:∠A=600、∠B=450、BC=3cm
B
C
A
750
450
3cm
两角和其中一角的对边对应相等的两个三角形全等,简写成角角边或AAS
剪下来,与同伴进行比较,它们能否互相重合?
画法先算出∠C=750,接下来与ASA画法一样
750
在△ABC与△DEF中,
∴△ABC≌△DEF(ASA)
A
B
C
D
E
F
已知:∠B=∠E, ∠A=∠D,BC=EF,判断:△ABC和△DEF全等吗?
解:在△ABC中, ∠C=180- ∠A- ∠B
在△DEF中, ∠F=180- ∠D- ∠E
又∵ ∠B=∠E, ∠A=∠D,
∴∠C=∠F
两角和其中一角的对边对应相等的两个三角形全等,简写成角角边或AAS
60°
45°
45°
60°
60°
45°
3CM
3CM
很显然这二个三角形不全等,不是相等角所对的边故
它们并不是AAS,
认真观察这二个三形的角边关系,会不会全等呢?
1.如图,∠B=∠C ,AD平分∠BAC,
试说明△ABD≌△ACD;若BD=3cm,则CD有多长?
解:∵AD平分∠BAC(已知)
∴∠1=∠2(角平分线的定义)
∴在△ABD和△ACD中
∠1=∠2(已证)
∠B=∠C(已知)
AD=AD(公共边)
∴△ABD≌△ACD(AAS)
∴CD=BD=3㎝(全等三角形的对应边相等)
1
2
A
B
C
D
E
1
2
2.如图,已知∠C=∠E,∠1=∠2,AB=AD,
△ABC和△ADE全等吗?为什么?
解: △ABC和△ADE全等,理由如下:
∵∠1=∠2(已知)
∴∠1+∠DAC=∠2+∠DAC
即∠BAC=∠DAE
在△ABC和△ADC 中
∴ △ABC≌△ADE
(AAS)
相等吗?
与
,那么
且
,
于
,
于
中,
已知
DC
BD
CF
BE
F
AD
CF
E
AD
BE
ABC
=
^
^
△
3
议一议
小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么?
有二个角的那一块,因为二角及夹边确定了一个三角形
本课小结
1.如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?
A
B
C
D
1
3
4
2
作业
∵ AB∥CD,AD∥BC(已知 )
∴ ∠1=∠2
∠3=∠4
∴在△ABC与△CDA中
∠1=∠2 (已证)
AC=AC (公共边)
∠3=∠4 (已证)
∴ △ABC≌△CDA(ASA)
∴ AB=CD BC=AD(全等三角形对应边相等)
解:相等,理由如下
连接AC
(两直线平行,内错角相等)
2.如图,∠C=∠D,DE=EC,
求证:(1)△DEB≌△CEA;(2)OA=OB.
∴△OAD≌△OBC(AAS),∴OA=OB.
∴△DEB≌△CEA(ASA)
证明:(1)在△DEB与△CEA中,
∠D=∠C
DE=EC
∠DEB=∠CEA
∠D=∠C
∠O=∠O
BC=AD
(2)∵△DEB≌△CEA,∴BE=EA,
∵DE=EC,∴BE+DE=EC+EA 即AD=BC,
在△OAD与△OBC中,
3.如图,AC∥DF,点B为线段AC上一点,连接BF交DC于点H,过点A作AE∥BF分别交DC,DF于点G,点E,DG=CH,试说明:△DFH≌△CAG.
解:因为AC∥DF,AE∥BF,所以∠C=∠D,∠AGC=∠DHF.因为DG=CH,所以CH+HG=HG+DG,即CG=DH.在△DFH和△CAG中,
∠AGC=∠DHF,CG=DH,∠C=∠D
所以△DFH≌△CAG(ASA).
4. 如图4-3-35,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,D为AB的中点,点P在线段上以3 cm/s的速度由点B向点C运动,同时,点Q在线
段CA上以相同速度由点C向点A运
动,一个点到达终点后另一个点
也停止运动.当△BPD与△CQP全
等时,求点P运动的时间.
解:因为∠B=∠C,所以AB=AC.
设点P,Q的运动时间为t,则
BP=3t,CQ=3t.
因为AB=10 cm,BC=8 cm,点D为AB的中点,
所以BD= ×10=5(cm),
PC=(8-3t)cm.
①BD,PC是对应边时,因为△BPD与△CQP全等,
所以BD=PC,BP=CQ.
所以5=8-3t且3t=3t.
解得t=1s.
×
×
10
8
×
×
10
8
②BD与CQ是对应边时,因为△BPD与△CQP全等,
所以BD=CQ,BP=PC.
所以5=3t,3t=8-3t.
解得t= 且t= (舍去).
综上所述,△BPD与△CQP全等时,点P运动的时间为
1 s.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
七年级下
4.3全等三角形的判定
角边角与角角边(第2课时)
①三角;
②三边;
④两边一角;
③两角一边。
如果满足三个条件,画出的三角形一定全等吗?
探索三角形全等的条件
③两角一边。
1.有角边角(ASA) 和 2.角角边(AAS)这二种情况
做一做
1、角.边.角;
若三角形的两个内角分别是60°和80°它们所夹的边为2cm,你能画出这个三角形吗?
2cm
60°
80°
60°
80°
2cm
做法一
60°
80°
2cm
做法二
另外再做一做:按要求画出三角形,并与同伴交流 。已知:∠A=600、∠B=450、AB=3cm
A
B
C
600
450
3cm
两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”
剪下来,与同伴进行比较,它们能否互相重合?
做法三
在△ABC与△DEF中,
∴△ABC≌△DEF(ASA)
几何语言:
A
B
C
D
E
F
已知:如图 ∠1=∠4, ∠2=∠3
试说明:△ACB≌ △BDA
解:
在△ACB和△BDA中
∠1=∠4(已知)
AB=BA(公共边)
∠2=∠3(已知)
∴ △ACB≌ △BDA(ASA)
已知:如图 AC∥BD,AD∥BC
试说明:△ACB≌ △BDA
在△ACB和△BDA中
∠1=∠4(已证)
AB=BA(公共边)
∠2=∠3(已证)
∴ △ACB≌ △BDA(ASA)
∴∠2=∠3(两直线平行,内错角相等)
∵AC∥BD(已知)
∴∠1=∠4(两直线平行,内错角相等)
∵AD∥BC(已知)
∴
解:
变式训练
如图,O是AB的中点,∠A=∠B,△AOC与△BOD全等吗?为什么?
A
B
C
D
O
△AOC △BOD
∠A=∠B
≌
AO=OB
∠AOC=∠BOD
(已知)
(中点定义)
(对顶角相等)
(ASA)
解:全等。理由如下
2、角.角.边
若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗?
60°
45°
已知:∠A=600、∠B=450、BC=3cm
B
C
A
750
450
3cm
两角和其中一角的对边对应相等的两个三角形全等,简写成角角边或AAS
剪下来,与同伴进行比较,它们能否互相重合?
画法先算出∠C=750,接下来与ASA画法一样
750
在△ABC与△DEF中,
∴△ABC≌△DEF(ASA)
A
B
C
D
E
F
已知:∠B=∠E, ∠A=∠D,BC=EF,判断:△ABC和△DEF全等吗?
解:在△ABC中, ∠C=180- ∠A- ∠B
在△DEF中, ∠F=180- ∠D- ∠E
又∵ ∠B=∠E, ∠A=∠D,
∴∠C=∠F
两角和其中一角的对边对应相等的两个三角形全等,简写成角角边或AAS
60°
45°
45°
60°
60°
45°
3CM
3CM
很显然这二个三角形不全等,不是相等角所对的边故
它们并不是AAS,
认真观察这二个三形的角边关系,会不会全等呢?
1.如图,∠B=∠C ,AD平分∠BAC,
试说明△ABD≌△ACD;若BD=3cm,则CD有多长?
解:∵AD平分∠BAC(已知)
∴∠1=∠2(角平分线的定义)
∴在△ABD和△ACD中
∠1=∠2(已证)
∠B=∠C(已知)
AD=AD(公共边)
∴△ABD≌△ACD(AAS)
∴CD=BD=3㎝(全等三角形的对应边相等)
1
2
A
B
C
D
E
1
2
2.如图,已知∠C=∠E,∠1=∠2,AB=AD,
△ABC和△ADE全等吗?为什么?
解: △ABC和△ADE全等,理由如下:
∵∠1=∠2(已知)
∴∠1+∠DAC=∠2+∠DAC
即∠BAC=∠DAE
在△ABC和△ADC 中
∴ △ABC≌△ADE
(AAS)
相等吗?
与
,那么
且
,
于
,
于
中,
已知
DC
BD
CF
BE
F
AD
CF
E
AD
BE
ABC
=
^
^
△
3
议一议
小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么?
有二个角的那一块,因为二角及夹边确定了一个三角形
本课小结
1.如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?
A
B
C
D
1
3
4
2
作业
∵ AB∥CD,AD∥BC(已知 )
∴ ∠1=∠2
∠3=∠4
∴在△ABC与△CDA中
∠1=∠2 (已证)
AC=AC (公共边)
∠3=∠4 (已证)
∴ △ABC≌△CDA(ASA)
∴ AB=CD BC=AD(全等三角形对应边相等)
解:相等,理由如下
连接AC
(两直线平行,内错角相等)
2.如图,∠C=∠D,DE=EC,
求证:(1)△DEB≌△CEA;(2)OA=OB.
∴△OAD≌△OBC(AAS),∴OA=OB.
∴△DEB≌△CEA(ASA)
证明:(1)在△DEB与△CEA中,
∠D=∠C
DE=EC
∠DEB=∠CEA
∠D=∠C
∠O=∠O
BC=AD
(2)∵△DEB≌△CEA,∴BE=EA,
∵DE=EC,∴BE+DE=EC+EA 即AD=BC,
在△OAD与△OBC中,
3.如图,AC∥DF,点B为线段AC上一点,连接BF交DC于点H,过点A作AE∥BF分别交DC,DF于点G,点E,DG=CH,试说明:△DFH≌△CAG.
解:因为AC∥DF,AE∥BF,所以∠C=∠D,∠AGC=∠DHF.因为DG=CH,所以CH+HG=HG+DG,即CG=DH.在△DFH和△CAG中,
∠AGC=∠DHF,CG=DH,∠C=∠D
所以△DFH≌△CAG(ASA).
4. 如图4-3-35,在△ABC中,∠B=∠C,AB=10 cm,BC=8 cm,D为AB的中点,点P在线段上以3 cm/s的速度由点B向点C运动,同时,点Q在线
段CA上以相同速度由点C向点A运
动,一个点到达终点后另一个点
也停止运动.当△BPD与△CQP全
等时,求点P运动的时间.
解:因为∠B=∠C,所以AB=AC.
设点P,Q的运动时间为t,则
BP=3t,CQ=3t.
因为AB=10 cm,BC=8 cm,点D为AB的中点,
所以BD= ×10=5(cm),
PC=(8-3t)cm.
①BD,PC是对应边时,因为△BPD与△CQP全等,
所以BD=PC,BP=CQ.
所以5=8-3t且3t=3t.
解得t=1s.
×
×
10
8
×
×
10
8
②BD与CQ是对应边时,因为△BPD与△CQP全等,
所以BD=CQ,BP=PC.
所以5=3t,3t=8-3t.
解得t= 且t= (舍去).
综上所述,△BPD与△CQP全等时,点P运动的时间为
1 s.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
