4.3.1 全等三角形的判定 课件(共24张PPT)
文档属性
| 名称 | 4.3.1 全等三角形的判定 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 21:07:47 | ||
图片预览



文档简介
数学北师大版
七年级下
4.3全等三角形的判定
边边边(第1课时)
1. 什么叫全等三角形?
能够重合的两个三角形叫 全等三角形.
2. 全等三角形有什么性质?
全等三角形的对应边相等,对应角相等.
温故知新
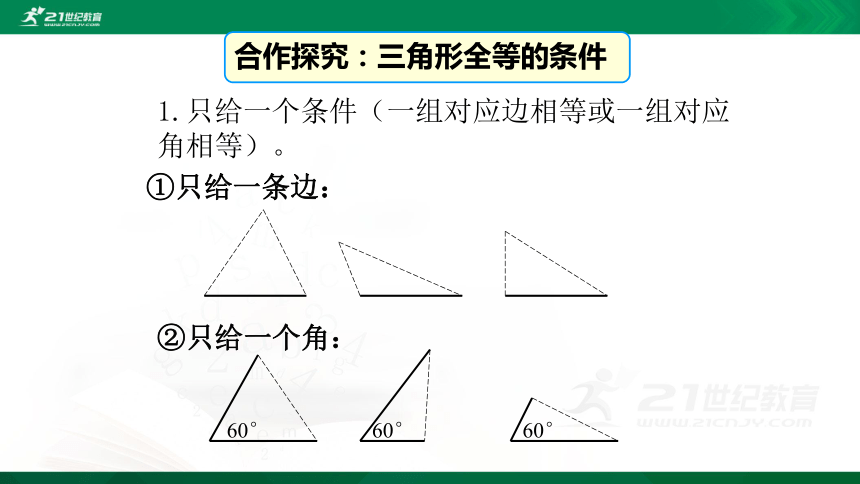
1.只给一个条件(一组对应边相等或一组对应角相等)。
①只给一条边:
②只给一个角:
60°
60°
60°
讲授新课
合作探究:三角形全等的条件
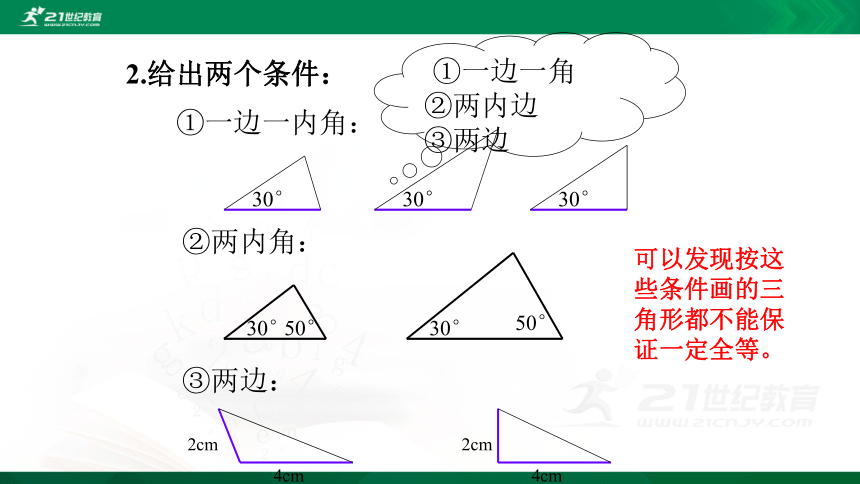
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
可以发现按这些条件画的三角形都不能保证一定全等。
①一边一角
②两内边
③两边
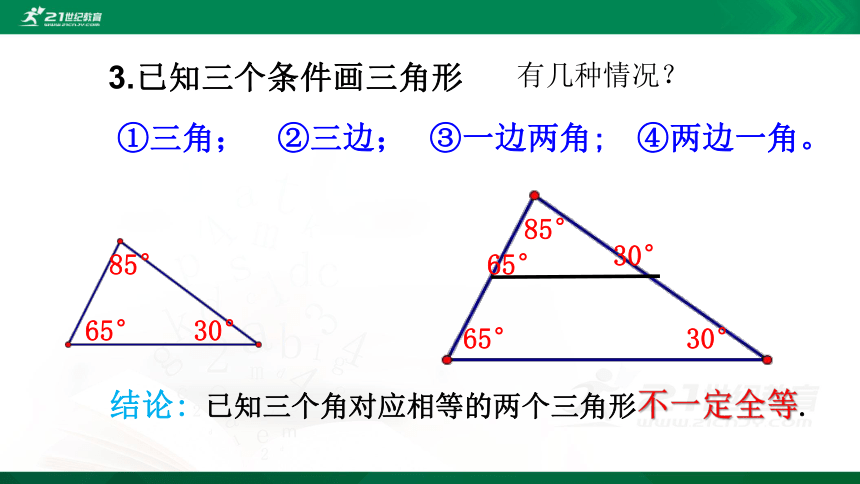
3.已知三个条件画三角形
有几种情况?
②三边;
④两边一角。
③一边两角;
①三角;
30°
65°
85°
85°
65°
30°
30°
65°
结论: 已知三个角对应相等的两个三角形不一定全等.
A
B
C
5cm
4cm
6cm
5cm
4cm
6cm
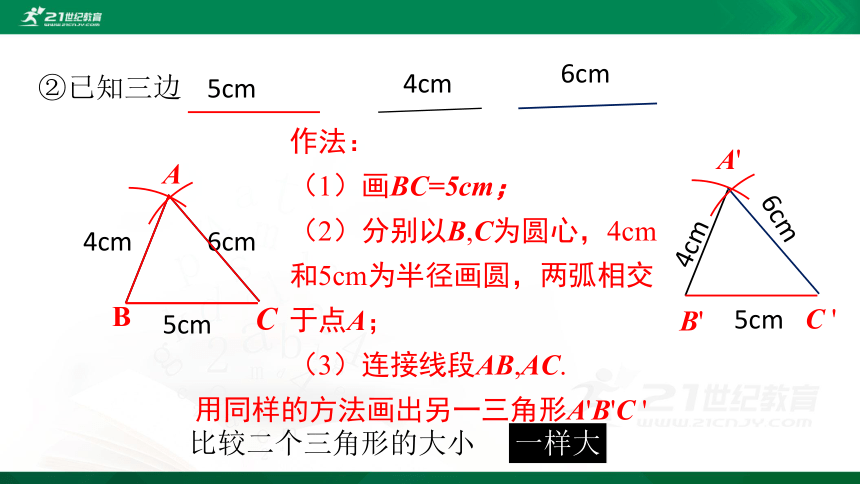
作法:
(1)画BC=5cm;
(2)分别以B,C为圆心,4cm和5cm为半径画圆,两弧相交于点A;
(3)连接线段AB,AC.
A'
B'
C '
②已知三边
用同样的方法画出另一三角形A'B'C '
5cm
4cm
6cm
比较二个三角形的大小
一样大
先任意画出一个△ABC,再画出一个△A′B′C′ ,使A′B′= AB ,B′C′ =BC, A′ C′ =AC.把画好的△A′B′C′剪下,放到△ABC上,他们全等吗?
A
B
C
做一做
作法:
(1)画B′C′=BC;
(2)分别以B',C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A';
(3)连接线段A'B',A 'C '.
B′
C′
A′
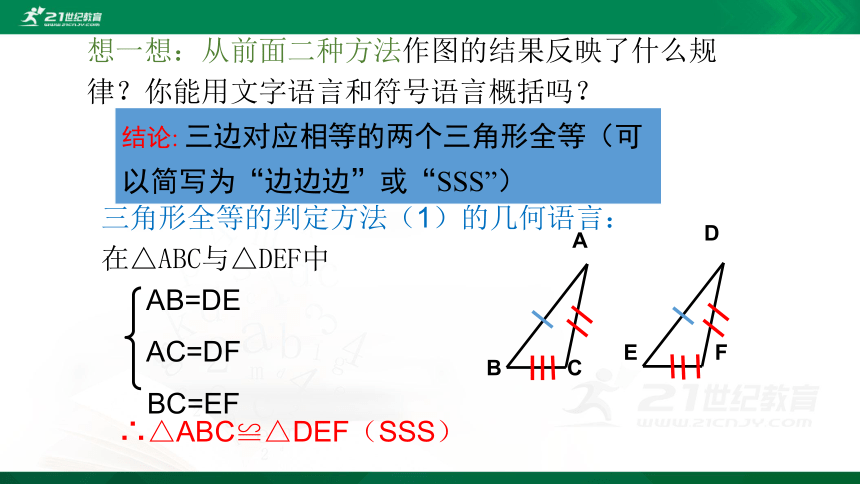
想一想:从前面二种方法作图的结果反映了什么规律?你能用文字语言和符号语言概括吗?
三角形全等的判定方法(1)的几何语言:
在△ABC与△DEF中
A
B
C
D
E
F
AB=DE
AC=DF
BC=EF
∴△ABC≌△DEF(SSS)
结论: 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)
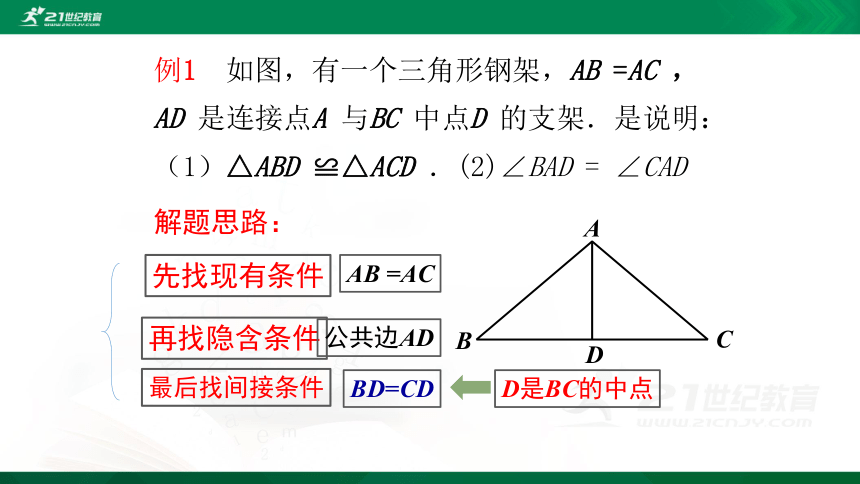
例1 如图,有一个三角形钢架,AB =AC ,AD 是连接点A 与BC 中点D 的支架.是说明:(1)△ABD ≌△ACD .(2)∠BAD = ∠CAD
C
B
D
A
解题思路:
先找现有条件
AB =AC
再找隐含条件
公共边AD
最后找间接条件
BD=CD
D是BC的中点
例1 如图,有一个三角形钢架,AB =AC ,AD 是连接点A 与BC 中点D 的支架.是说明:(1)△ABD ≌△ACD .(2)∠BAD = ∠CAD
C
B
D
A
解:
AB =AC(已知)
BD=CD
AD=AD(公共边)
所以△ABD ≌△ACD
故∠BAD = ∠CAD(全等三角形对应角相等)
(中点定义)
(SSS)
变式训练
1.已知:如图,AB=AC,DB=DC,请说明∠B =∠C成立的理由.
A
B
C
D
构造公共边是常添加的辅助线!
AB=AC,
DB=DC,
AD=AD
△ABD ≌△ACD (SSS).
所以∠B = ∠C
(已知)
(已知)
(公共边)
(全等三角形对应角相等)
理由:
变式训练
2.已知:如图AB=CD,AD=BC.则∠A与∠C相等吗?为什么?
A
B
C
D
构造公共边是常添加的辅助线!
解:相等.理由如下:
AB=CD,
AD=BC
BD=BD
(已知)
(已知)
(公共边)
△ABD ≌△CDB (SSS).
所以∠A = ∠C
(全等三角形对应角相等)
3.如图,D、F是线段BC上的两点,AB=DE,AC=DF,BE=CF,那么∠ACF = ∠DEB吗?
变式训练
△ABC≌△DEF(SSS)
解:会相等,理由如下:
由BE=CF(已知)得:
BE+EC=CF+CE(等式性质)
即BC=FE
AB=DE,AC=DF
(已知)
∠ACB = ∠DEF
∠ACF = ∠DEB
(全等三角形对应角相等)
(等角的补角相等)
如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?
H
D
C
B
A
解:有三组。 在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);
∵BD=CD,BH=CH,DH=DH
∴△DBH≌△DCH(SSS)
在△ABD和△ACD中
∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);
在△DBH和△DCH中
巩固达标
只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这是三角形具有稳定性.
你知道它们为什么设计成三角形的样子吗?
想一想
本课小结
1. 三角形全等的条件:
三边对应相等的两个三角形全等
(“边边边”或“SSS”)
2. 三角形具有稳定性。
1.如图,AB=AE,AC=AD,BD=CE.
求证:△ABC≌△AED
2.如图,已知AC =FE,BC=DE,点A,D,B,F在一条直线上,AD=FB,
求证:△ABC≌△ FDE.
课后作业
1.如图,AB=AE,AC=AD,BD=CE.
求证:△ABC≌△AED
课后作业
证明:由BD=CE(已知)得:
BD-CD=CE-CD
即BC=ED
AB=AE,
AC=AD
△ABC≌△AED
(等式性质)
(已知)
(已知)
BC=ED
(已证)
(SSS)
2.如图,已知AC =FE,BC=DE,点A,D,B,F在一条直线上,AD=FB,
求证:△ABC≌△ FDE.
课后作业
证明:由AD=FB(已知)得
AD+DB=FB+BD
即AB=FD
(等式性质)
AC =FE,BC=DE
(已知)
△ABC≌△ FDE.
(SSS)
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
七年级下
4.3全等三角形的判定
边边边(第1课时)
1. 什么叫全等三角形?
能够重合的两个三角形叫 全等三角形.
2. 全等三角形有什么性质?
全等三角形的对应边相等,对应角相等.
温故知新
1.只给一个条件(一组对应边相等或一组对应角相等)。
①只给一条边:
②只给一个角:
60°
60°
60°
讲授新课
合作探究:三角形全等的条件
2.给出两个条件:
①一边一内角:
②两内角:
③两边:
30°
30°
30°
30°
30°
50°
50°
2cm
2cm
4cm
4cm
可以发现按这些条件画的三角形都不能保证一定全等。
①一边一角
②两内边
③两边
3.已知三个条件画三角形
有几种情况?
②三边;
④两边一角。
③一边两角;
①三角;
30°
65°
85°
85°
65°
30°
30°
65°
结论: 已知三个角对应相等的两个三角形不一定全等.
A
B
C
5cm
4cm
6cm
5cm
4cm
6cm
作法:
(1)画BC=5cm;
(2)分别以B,C为圆心,4cm和5cm为半径画圆,两弧相交于点A;
(3)连接线段AB,AC.
A'
B'
C '
②已知三边
用同样的方法画出另一三角形A'B'C '
5cm
4cm
6cm
比较二个三角形的大小
一样大
先任意画出一个△ABC,再画出一个△A′B′C′ ,使A′B′= AB ,B′C′ =BC, A′ C′ =AC.把画好的△A′B′C′剪下,放到△ABC上,他们全等吗?
A
B
C
做一做
作法:
(1)画B′C′=BC;
(2)分别以B',C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A';
(3)连接线段A'B',A 'C '.
B′
C′
A′
想一想:从前面二种方法作图的结果反映了什么规律?你能用文字语言和符号语言概括吗?
三角形全等的判定方法(1)的几何语言:
在△ABC与△DEF中
A
B
C
D
E
F
AB=DE
AC=DF
BC=EF
∴△ABC≌△DEF(SSS)
结论: 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)
例1 如图,有一个三角形钢架,AB =AC ,AD 是连接点A 与BC 中点D 的支架.是说明:(1)△ABD ≌△ACD .(2)∠BAD = ∠CAD
C
B
D
A
解题思路:
先找现有条件
AB =AC
再找隐含条件
公共边AD
最后找间接条件
BD=CD
D是BC的中点
例1 如图,有一个三角形钢架,AB =AC ,AD 是连接点A 与BC 中点D 的支架.是说明:(1)△ABD ≌△ACD .(2)∠BAD = ∠CAD
C
B
D
A
解:
AB =AC(已知)
BD=CD
AD=AD(公共边)
所以△ABD ≌△ACD
故∠BAD = ∠CAD(全等三角形对应角相等)
(中点定义)
(SSS)
变式训练
1.已知:如图,AB=AC,DB=DC,请说明∠B =∠C成立的理由.
A
B
C
D
构造公共边是常添加的辅助线!
AB=AC,
DB=DC,
AD=AD
△ABD ≌△ACD (SSS).
所以∠B = ∠C
(已知)
(已知)
(公共边)
(全等三角形对应角相等)
理由:
变式训练
2.已知:如图AB=CD,AD=BC.则∠A与∠C相等吗?为什么?
A
B
C
D
构造公共边是常添加的辅助线!
解:相等.理由如下:
AB=CD,
AD=BC
BD=BD
(已知)
(已知)
(公共边)
△ABD ≌△CDB (SSS).
所以∠A = ∠C
(全等三角形对应角相等)
3.如图,D、F是线段BC上的两点,AB=DE,AC=DF,BE=CF,那么∠ACF = ∠DEB吗?
变式训练
△ABC≌△DEF(SSS)
解:会相等,理由如下:
由BE=CF(已知)得:
BE+EC=CF+CE(等式性质)
即BC=FE
AB=DE,AC=DF
(已知)
∠ACB = ∠DEF
∠ACF = ∠DEB
(全等三角形对应角相等)
(等角的补角相等)
如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?
H
D
C
B
A
解:有三组。 在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);
∵BD=CD,BH=CH,DH=DH
∴△DBH≌△DCH(SSS)
在△ABD和△ACD中
∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);
在△DBH和△DCH中
巩固达标
只要三角形的三边的长度确定了,这个三角形的形状和大小就完全确定了,这是三角形具有稳定性.
你知道它们为什么设计成三角形的样子吗?
想一想
本课小结
1. 三角形全等的条件:
三边对应相等的两个三角形全等
(“边边边”或“SSS”)
2. 三角形具有稳定性。
1.如图,AB=AE,AC=AD,BD=CE.
求证:△ABC≌△AED
2.如图,已知AC =FE,BC=DE,点A,D,B,F在一条直线上,AD=FB,
求证:△ABC≌△ FDE.
课后作业
1.如图,AB=AE,AC=AD,BD=CE.
求证:△ABC≌△AED
课后作业
证明:由BD=CE(已知)得:
BD-CD=CE-CD
即BC=ED
AB=AE,
AC=AD
△ABC≌△AED
(等式性质)
(已知)
(已知)
BC=ED
(已证)
(SSS)
2.如图,已知AC =FE,BC=DE,点A,D,B,F在一条直线上,AD=FB,
求证:△ABC≌△ FDE.
课后作业
证明:由AD=FB(已知)得
AD+DB=FB+BD
即AB=FD
(等式性质)
AC =FE,BC=DE
(已知)
△ABC≌△ FDE.
(SSS)
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
