4.3.3 全等三角形的判定 课件(共20张PPT)
文档属性
| 名称 | 4.3.3 全等三角形的判定 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 21:10:51 | ||
图片预览




文档简介
数学北师大版
七年级下
4.3全等三角形的判定
边角边(第3课时)
①三角;
②三边;
④两边一角有二种情况;
③两角一边。
如果满足三个条件,画出的三角形一定全等吗?
探索三角形全等的条件
④两边一角;
(1)两边及其夹角(2)两边和其中一边的对角
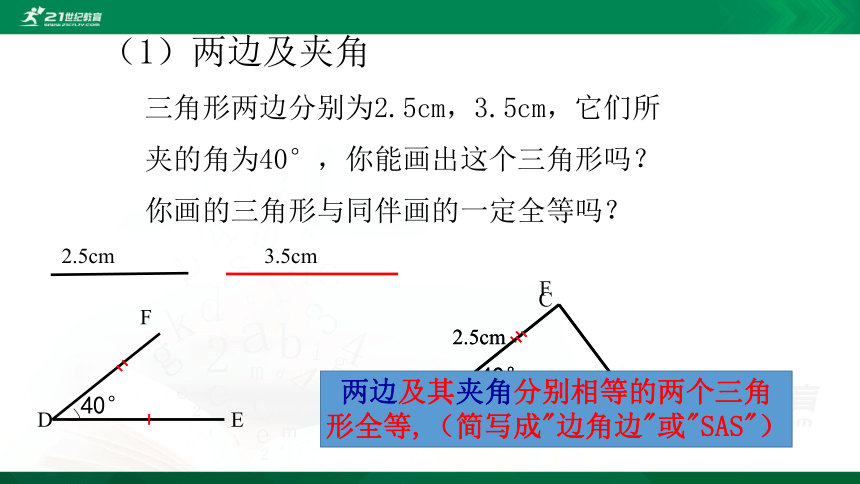
(1)两边及夹角
三角形两边分别为2.5cm,3.5cm,它们所
夹的角为40°,你能画出这个三角形吗?
你画的三角形与同伴画的一定全等吗?
3.5cm
2.5cm
40°
A
B
C
3.5cm
2.5cm
40°
D
E
F
40°
D
E
F
2.5cm
3.5cm
两边及其夹角分别相等的两个三角形全等,(简写成"边角边"或"SAS")
A
B
C
D
E
F
∟
∟
D
E
F
∟
∟
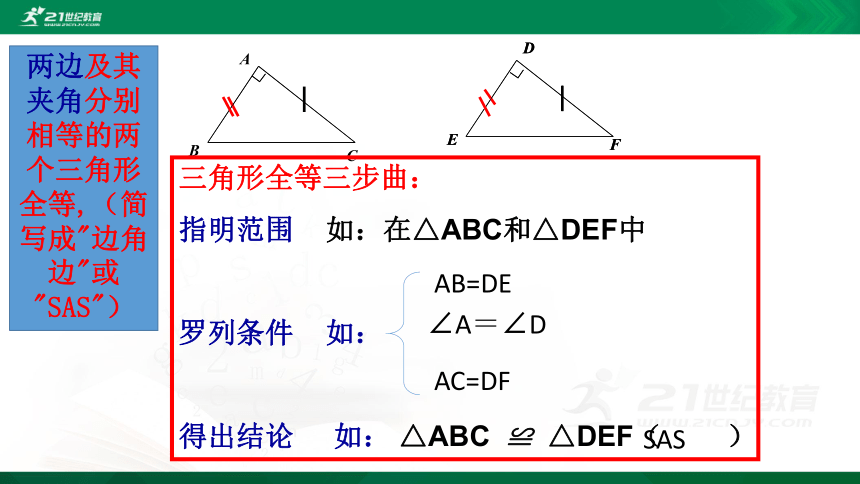
三角形全等三步曲:
指明范围 如:在△ABC和△DEF中
罗列条件 如:
得出结论 如: △ABC ≌ △DEF( )
AC=DF
AB=DE
∠A=∠D
SAS
两边及其夹角分别相等的两个三角形全等,(简写成"边角边"或"SAS")
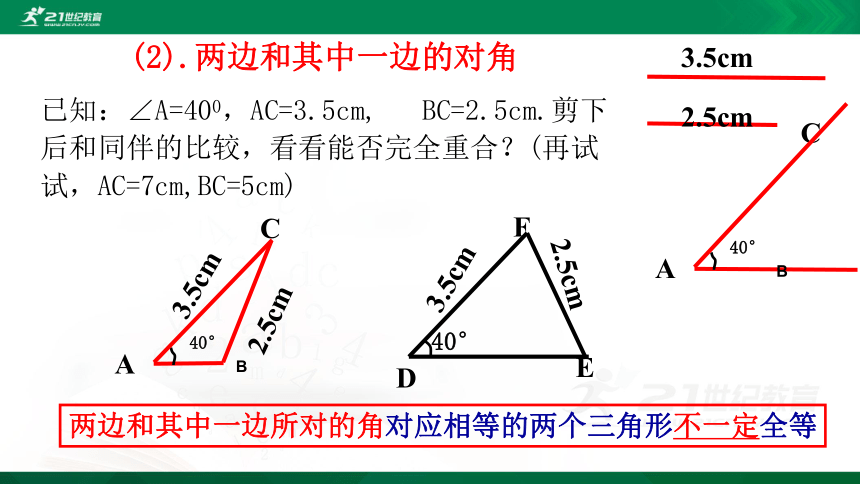
(2).两边和其中一边的对角
两边和其中一边所对的角对应相等的两个三角形不一定全等
E
D
F
40°
3.5cm
2.5cm
A
C
2.5cm
3.5cm
40°
B
已知:∠A=400,AC=3.5cm, BC=2.5cm.剪下后和同伴的比较,看看能否完全重合?(再试试,AC=7cm,BC=5cm)
2.5cm
3.5cm
A
C
40°
B
1. 今天我们学习哪种方法判定两三角形全等?
边角边(SAS)
2. 通过这节课,判定三角形全等的条件有哪些?
SSS,SAS,ASA,AAS
3.在这四种说明三角形全等的条件中,你发现了什么?
至少有一个条件:边相等
“边边角”不能判定两个三角形全等
归纳总结
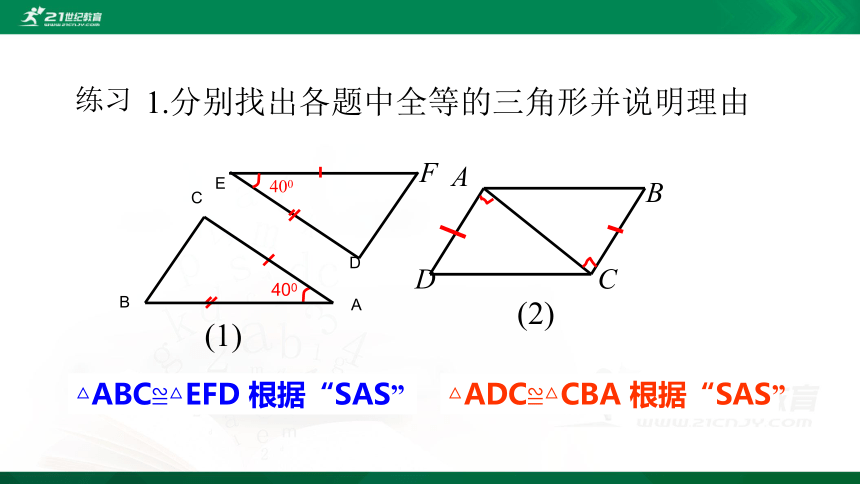
1.分别找出各题中全等的三角形并说明理由
D
C
A
B
(2)
(1)
F
400
E
D
A
B
C
400
练习
△ADC≌△CBA 根据“SAS”
△ABC≌△EFD 根据“SAS”
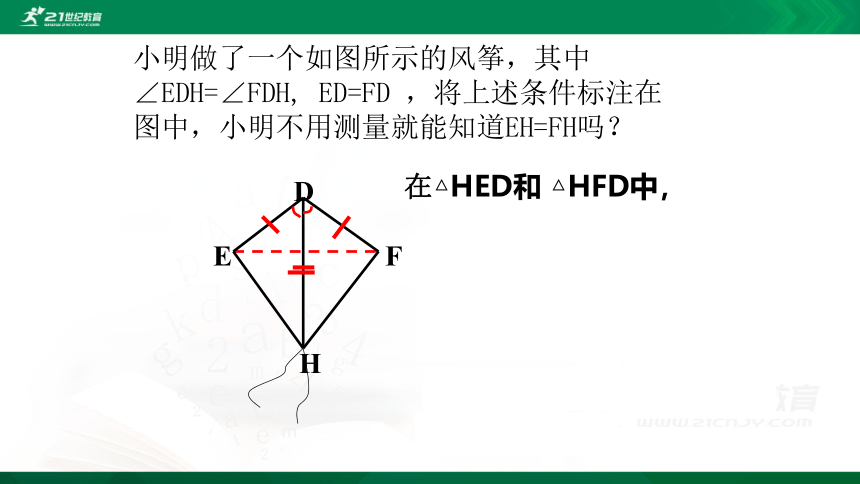
小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?
E
F
D
H
在△HED和 △HFD中,
△HED ≌ △HFD (SAS)
变式
如图,在一个风筝ABCD中,AB=AD,BC=DC分别在AB,AD的中点E,F处挂两根彩线EC,FC,试说明;EC=FC
在△ABC和△ADC中,
AC=AC,
BC= DC,
AB=AD
∴△ABC≌△ADC(SSS),
∴∠EAC=∠FAC.
∵E,F分别是AB ,AD的中点,
解:如图,连接AC.
AE= AB, AF= AD.
∵AB=AD,
在△AEC和△AFC中,∠EAC=∠FAC,AC=AC,AE=AF,
∴△AEC≌△AFC(SAS),
∴EC= FC.
∴AE=AF.
1.已知:如图,AD∥BC,AD=CB,
求证:DC=BA.
AD=CB(已知)
∠1=∠2(已知)
AC=CA (公共边)
∴ △ADC≌△CBA(SAS).
【证明】∵ AD∥BC,
∴ ∠1=∠2(两直线平行,内错角相等).
在△DAC和△BCA中,
D
C
1
A
2
B
∴ DC=BA
提高训练
B
C
D
E
A
2,如图,已知AB=AC,AD=AE。
求证:∠B=∠C
C
E
A
B
A
D
证明:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形
对应角相等)
例1:如图,已知△ABC中,BE和CD分别为∠B和∠C的平分线,且BD = CE,∠1 = ∠2.
求证:BE = CD
A
B
C
E
D
1
2
证明:
∵∠DBC = 2∠1,∠ECB = 2∠2
(角平分线的定义)
∠1 = ∠2
∴∠DBC = ∠ECB
∵在△DBC和△ECB中
BD = CE
∠DBC = ∠ECB
BC = CB(公共边)
∴ △DBC≌△ECB(SAS)
∴BE = CD(全等三角形的对应边相等)
如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与△FED全等吗?为什么?
AC∥FD吗?为什么?
F
E
D
C
B
A
4
3
1
2
在△ABC与△FED中
解:全等。
∵BD=EC ∴BD-CD=EC-CD。即BC=ED
∴△ABC≌△FED(SAS)
∴∠1=∠2
∴∠3=∠4
∴AC∥FD
(全等三角形对应角相等)
(等角的补角相等)
(内错角相等,两直线平行)
例2:
本课小结
1.如图所示,OD=OB,AD∥BC,则全等三
角形有( )
(A)2对 (B)3对
(C)4对 (D)5对
【解析】选C.根据题意AD∥BC得∠ADO=∠CBO,∠DOA=∠BOC,又OD=OB,所以△DOA≌△BOC同理可证△DOC≌△BOA,△DAB≌△BCD,△ACD≌△CAB,所以有4对.
课后作业
2.如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B,D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为_________.
【解析】因为四边形ABCD是正方形,所以AB=AD,
∠ABC=∠BAD=90°.
因为BF⊥a于点F,DE⊥a于点E,
所以∠FAB+∠FBA=∠FAB+∠EAD=90°,所以∠FBA=∠EAD.
所以在Rt△AFB和Rt△AED中,因为∠AFB=∠DEA=90°,∠FBA=∠EAD ,AB=DA,所以△AFB≌△DEA(AAS),
所以AF=DE=8,BF=AE=5,所以EF=AF+AE=8+5=13.答案:13
3.如图①,A,B,C,D在同一直线上,AB=CD,DE∥AF,且DE=AF,试说明:△AFC≌△DEB.如果将BD沿着AD边的方向平行移动,如图②,③时,其余条件不变,结论是否成立?如果成立,请予以说明;如果不成立,请说明理由.
解:因为AB=CD,所以AB+BC=CD+BC,即AC=BD.因为DE∥AF,所以∠A=∠D.又因为AF=DE,故△AFC≌△DEB(SAS).在图②,③中结论依然成立.说明如下:在图②中说明略;在图③中,因为AB=CD,所以AB-BC=CD-BC,即AC=BD,因为AF∥DE,所以∠A=∠D.又因为AF=DE,所以△AFC≌△DEB(SAS).
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
七年级下
4.3全等三角形的判定
边角边(第3课时)
①三角;
②三边;
④两边一角有二种情况;
③两角一边。
如果满足三个条件,画出的三角形一定全等吗?
探索三角形全等的条件
④两边一角;
(1)两边及其夹角(2)两边和其中一边的对角
(1)两边及夹角
三角形两边分别为2.5cm,3.5cm,它们所
夹的角为40°,你能画出这个三角形吗?
你画的三角形与同伴画的一定全等吗?
3.5cm
2.5cm
40°
A
B
C
3.5cm
2.5cm
40°
D
E
F
40°
D
E
F
2.5cm
3.5cm
两边及其夹角分别相等的两个三角形全等,(简写成"边角边"或"SAS")
A
B
C
D
E
F
∟
∟
D
E
F
∟
∟
三角形全等三步曲:
指明范围 如:在△ABC和△DEF中
罗列条件 如:
得出结论 如: △ABC ≌ △DEF( )
AC=DF
AB=DE
∠A=∠D
SAS
两边及其夹角分别相等的两个三角形全等,(简写成"边角边"或"SAS")
(2).两边和其中一边的对角
两边和其中一边所对的角对应相等的两个三角形不一定全等
E
D
F
40°
3.5cm
2.5cm
A
C
2.5cm
3.5cm
40°
B
已知:∠A=400,AC=3.5cm, BC=2.5cm.剪下后和同伴的比较,看看能否完全重合?(再试试,AC=7cm,BC=5cm)
2.5cm
3.5cm
A
C
40°
B
1. 今天我们学习哪种方法判定两三角形全等?
边角边(SAS)
2. 通过这节课,判定三角形全等的条件有哪些?
SSS,SAS,ASA,AAS
3.在这四种说明三角形全等的条件中,你发现了什么?
至少有一个条件:边相等
“边边角”不能判定两个三角形全等
归纳总结
1.分别找出各题中全等的三角形并说明理由
D
C
A
B
(2)
(1)
F
400
E
D
A
B
C
400
练习
△ADC≌△CBA 根据“SAS”
△ABC≌△EFD 根据“SAS”
小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?
E
F
D
H
在△HED和 △HFD中,
△HED ≌ △HFD (SAS)
变式
如图,在一个风筝ABCD中,AB=AD,BC=DC分别在AB,AD的中点E,F处挂两根彩线EC,FC,试说明;EC=FC
在△ABC和△ADC中,
AC=AC,
BC= DC,
AB=AD
∴△ABC≌△ADC(SSS),
∴∠EAC=∠FAC.
∵E,F分别是AB ,AD的中点,
解:如图,连接AC.
AE= AB, AF= AD.
∵AB=AD,
在△AEC和△AFC中,∠EAC=∠FAC,AC=AC,AE=AF,
∴△AEC≌△AFC(SAS),
∴EC= FC.
∴AE=AF.
1.已知:如图,AD∥BC,AD=CB,
求证:DC=BA.
AD=CB(已知)
∠1=∠2(已知)
AC=CA (公共边)
∴ △ADC≌△CBA(SAS).
【证明】∵ AD∥BC,
∴ ∠1=∠2(两直线平行,内错角相等).
在△DAC和△BCA中,
D
C
1
A
2
B
∴ DC=BA
提高训练
B
C
D
E
A
2,如图,已知AB=AC,AD=AE。
求证:∠B=∠C
C
E
A
B
A
D
证明:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形
对应角相等)
例1:如图,已知△ABC中,BE和CD分别为∠B和∠C的平分线,且BD = CE,∠1 = ∠2.
求证:BE = CD
A
B
C
E
D
1
2
证明:
∵∠DBC = 2∠1,∠ECB = 2∠2
(角平分线的定义)
∠1 = ∠2
∴∠DBC = ∠ECB
∵在△DBC和△ECB中
BD = CE
∠DBC = ∠ECB
BC = CB(公共边)
∴ △DBC≌△ECB(SAS)
∴BE = CD(全等三角形的对应边相等)
如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与△FED全等吗?为什么?
AC∥FD吗?为什么?
F
E
D
C
B
A
4
3
1
2
在△ABC与△FED中
解:全等。
∵BD=EC ∴BD-CD=EC-CD。即BC=ED
∴△ABC≌△FED(SAS)
∴∠1=∠2
∴∠3=∠4
∴AC∥FD
(全等三角形对应角相等)
(等角的补角相等)
(内错角相等,两直线平行)
例2:
本课小结
1.如图所示,OD=OB,AD∥BC,则全等三
角形有( )
(A)2对 (B)3对
(C)4对 (D)5对
【解析】选C.根据题意AD∥BC得∠ADO=∠CBO,∠DOA=∠BOC,又OD=OB,所以△DOA≌△BOC同理可证△DOC≌△BOA,△DAB≌△BCD,△ACD≌△CAB,所以有4对.
课后作业
2.如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B,D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为_________.
【解析】因为四边形ABCD是正方形,所以AB=AD,
∠ABC=∠BAD=90°.
因为BF⊥a于点F,DE⊥a于点E,
所以∠FAB+∠FBA=∠FAB+∠EAD=90°,所以∠FBA=∠EAD.
所以在Rt△AFB和Rt△AED中,因为∠AFB=∠DEA=90°,∠FBA=∠EAD ,AB=DA,所以△AFB≌△DEA(AAS),
所以AF=DE=8,BF=AE=5,所以EF=AF+AE=8+5=13.答案:13
3.如图①,A,B,C,D在同一直线上,AB=CD,DE∥AF,且DE=AF,试说明:△AFC≌△DEB.如果将BD沿着AD边的方向平行移动,如图②,③时,其余条件不变,结论是否成立?如果成立,请予以说明;如果不成立,请说明理由.
解:因为AB=CD,所以AB+BC=CD+BC,即AC=BD.因为DE∥AF,所以∠A=∠D.又因为AF=DE,故△AFC≌△DEB(SAS).在图②,③中结论依然成立.说明如下:在图②中说明略;在图③中,因为AB=CD,所以AB-BC=CD-BC,即AC=BD,因为AF∥DE,所以∠A=∠D.又因为AF=DE,所以△AFC≌△DEB(SAS).
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
