4.5 利用三角形全等测距离 课件(共19张PPT)
文档属性
| 名称 | 4.5 利用三角形全等测距离 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 21:13:22 | ||
图片预览




文档简介
数学北师大版
七年级下
4.5 利用三角形全等测距离
1.要证明两个三角形全等应有哪些必要条件?
(1)“SSS”:三边对应相等的两个三角形全等.
(2)“ASA”:两角和它们的夹边对应相等的两个三角形全等.
(3)“AAS”:两角和其中一角的对边对应相等的两个三角形全等.
(4)“SAS”:两边和它们的夹角对应相等的两个三角形全等.
复习引入
2.两个全等的三角形有哪些性质?
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等.
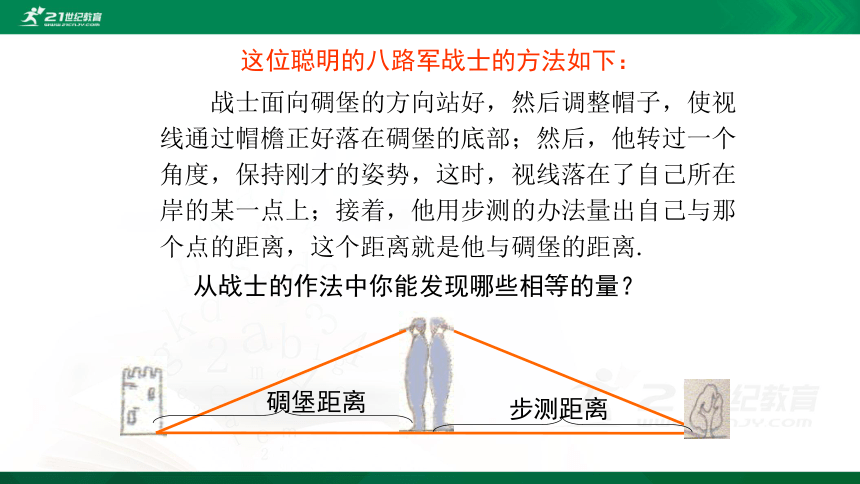
一位经历过战争的老人讲述过这样一个故事:为了炸毁与我军阵地隔河相望的日本鬼子的碉堡,需要测出我军阵地到鬼子碉堡的距离.由于没有任何测量工具,一位聪明的八路军战士想出了一个办法,为成功炸毁碉堡立了一功.
这位聪明的八路军战士的方法如下:
战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时,视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离.
步测距离
碉堡距离
从战士的作法中你能发现哪些相等的量?
?
A
B
C
D
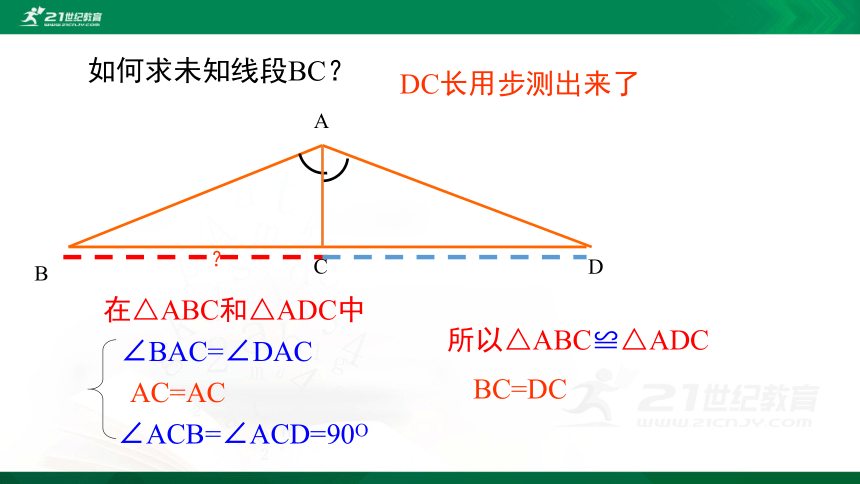
如何求未知线段BC?
AC=AC
在△ABC和△ADC中
∠ACB=∠ACD=90O
∠BAC=∠DAC
所以△ABC≌△ADC
BC=DC
DC长用步测出来了
C
D
E
·
·
·
B
A
·
·
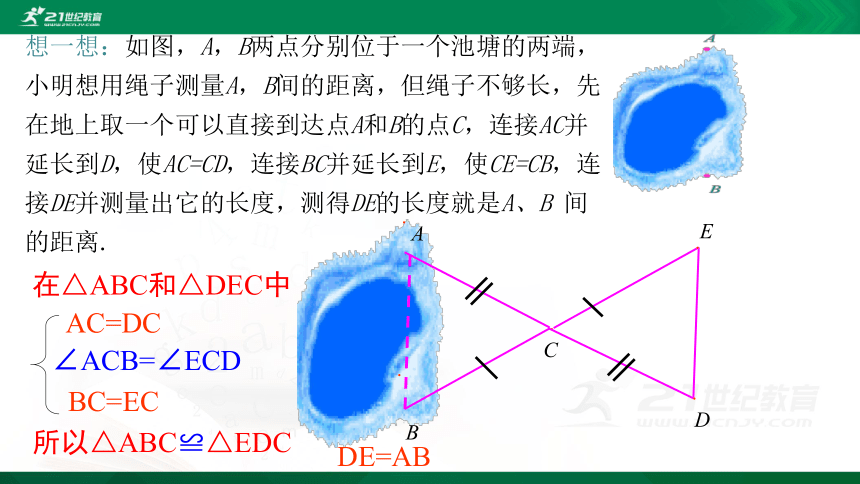
想一想:如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,先在地上取一个可以直接到达点A和B的点C,连接AC并延长到D,使AC=CD,连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,测得DE的长度就是A、B 间的距离.
在△ABC和△DEC中
AC=DC
∠ACB=∠ECD
BC=EC
所以△ABC≌△EDC
DE=AB
B
A
·
·
C
D
·
·
方案二
方案四
方案三
1.利用三角形全等测距离,主要是解决哪些问题?
不能到达或不能直接测量的两点之间的距离
如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长.判定△EDC≌△ABC的理由是( )
A.SSS B.ASA
C.AAS D.SAS
B
A
●
●
D
C
E
F
B
当堂练习
2.山脚下有A、B两点,要测出A、B两点间的距离.
在地上取一个可以直接到达A、B点的点O,连接
AO并延长到C,使AO=CO;连接BO并延长到D,
使BO=DO,连接CD.可以证△ABO≌△CDO,得
CD=AB,因此,测得CD的长就是AB的长.判定
△ABO≌△CDO的理由是( )
A.SSS B.ASA
C.AAS D.SAS
D
D
3.如图所示小明设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO 应满足下列的哪个条件?( )
A.AO=CO
B.BO=DO
C.AC=BD
D.AO=CO且BO=DO
O
D
C
B
A
D
例 把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5 cm和3 cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
A.4 cm B.6 cm
C.8 cm D.求不出来
解析:选C.
因为∠CEA=∠ADB=∠CAB=90°,
所以∠ECA+∠EAC=∠EAC+∠DAB
=∠DAB+∠DBA=90°,
∠ECA=∠DAB,∠EAC=∠DBA,
又AC=AB,所以△AEC ≌△BDA,
所以AE=BD,AD=CE,
所以DE=AE+AD=BD+CE=3+5=8 (cm).
1.知识:
利用三角形全等测距离的目的:变不可测距离为可测距离.
依据:全等三角形的性质.
关键:构造全等三角形.
2.方法:
(1)延长法构造全等三角形;
(2)垂直法构造全等三角形.
3.数学思想:
树立用三角形全等构建数学模型解决实际问题的思想.
课堂小结
1.已知如图,要测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点B′,
使∠ACB′=∠ACB,这时只要量出
AB′的长,就知道AB的长,对吗?
为什么?
解:对.理由:∵AC⊥AB
∴∠CAB=∠CAB′=90°
在△ABC和△AB′C中,
∵
∴△ABC≌△AB′C(ASA)
∴AB′=AB.
作业布置
∠CAB=∠CAB′
∠ACB′=∠ACB
AC=AC.
2.如图,小明家有一个玻璃容器,他想测量一下它的内径是多少,但是他无法将刻度尺伸进容器直接测量,于是他把两根长度相等的小木条AB,CD的中点连在一起,木条可以绕中点O自由转动,这样只要测量A,C的距离,就可以知道玻璃容器的内径,你知道其中的道理吗?请说明理由.
----------------
-------------
3. 如图4-5-17,是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的总长度为 ( )
A. 45 cm
B. 48 cm
C. 51 cm
D. 54 cm
A
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
七年级下
4.5 利用三角形全等测距离
1.要证明两个三角形全等应有哪些必要条件?
(1)“SSS”:三边对应相等的两个三角形全等.
(2)“ASA”:两角和它们的夹边对应相等的两个三角形全等.
(3)“AAS”:两角和其中一角的对边对应相等的两个三角形全等.
(4)“SAS”:两边和它们的夹角对应相等的两个三角形全等.
复习引入
2.两个全等的三角形有哪些性质?
(1)全等三角形的对应边相等;
(2)全等三角形的对应角相等.
一位经历过战争的老人讲述过这样一个故事:为了炸毁与我军阵地隔河相望的日本鬼子的碉堡,需要测出我军阵地到鬼子碉堡的距离.由于没有任何测量工具,一位聪明的八路军战士想出了一个办法,为成功炸毁碉堡立了一功.
这位聪明的八路军战士的方法如下:
战士面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿势,这时,视线落在了自己所在岸的某一点上;接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡的距离.
步测距离
碉堡距离
从战士的作法中你能发现哪些相等的量?
?
A
B
C
D
如何求未知线段BC?
AC=AC
在△ABC和△ADC中
∠ACB=∠ACD=90O
∠BAC=∠DAC
所以△ABC≌△ADC
BC=DC
DC长用步测出来了
C
D
E
·
·
·
B
A
·
·
想一想:如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,先在地上取一个可以直接到达点A和B的点C,连接AC并延长到D,使AC=CD,连接BC并延长到E,使CE=CB,连接DE并测量出它的长度,测得DE的长度就是A、B 间的距离.
在△ABC和△DEC中
AC=DC
∠ACB=∠ECD
BC=EC
所以△ABC≌△EDC
DE=AB
B
A
·
·
C
D
·
·
方案二
方案四
方案三
1.利用三角形全等测距离,主要是解决哪些问题?
不能到达或不能直接测量的两点之间的距离
如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长.判定△EDC≌△ABC的理由是( )
A.SSS B.ASA
C.AAS D.SAS
B
A
●
●
D
C
E
F
B
当堂练习
2.山脚下有A、B两点,要测出A、B两点间的距离.
在地上取一个可以直接到达A、B点的点O,连接
AO并延长到C,使AO=CO;连接BO并延长到D,
使BO=DO,连接CD.可以证△ABO≌△CDO,得
CD=AB,因此,测得CD的长就是AB的长.判定
△ABO≌△CDO的理由是( )
A.SSS B.ASA
C.AAS D.SAS
D
D
3.如图所示小明设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO 应满足下列的哪个条件?( )
A.AO=CO
B.BO=DO
C.AC=BD
D.AO=CO且BO=DO
O
D
C
B
A
D
例 把等腰直角三角形ABC,按如图所示立在桌上,顶点A顶着桌面,若另两个顶点距离桌面5 cm和3 cm,则过另外两个顶点向桌面作垂线,则垂足之间的距离DE的长为( )
A.4 cm B.6 cm
C.8 cm D.求不出来
解析:选C.
因为∠CEA=∠ADB=∠CAB=90°,
所以∠ECA+∠EAC=∠EAC+∠DAB
=∠DAB+∠DBA=90°,
∠ECA=∠DAB,∠EAC=∠DBA,
又AC=AB,所以△AEC ≌△BDA,
所以AE=BD,AD=CE,
所以DE=AE+AD=BD+CE=3+5=8 (cm).
1.知识:
利用三角形全等测距离的目的:变不可测距离为可测距离.
依据:全等三角形的性质.
关键:构造全等三角形.
2.方法:
(1)延长法构造全等三角形;
(2)垂直法构造全等三角形.
3.数学思想:
树立用三角形全等构建数学模型解决实际问题的思想.
课堂小结
1.已知如图,要测量水池的宽AB,可过点A作直线AC⊥AB,再由点C观测,在BA延长线上找一点B′,
使∠ACB′=∠ACB,这时只要量出
AB′的长,就知道AB的长,对吗?
为什么?
解:对.理由:∵AC⊥AB
∴∠CAB=∠CAB′=90°
在△ABC和△AB′C中,
∵
∴△ABC≌△AB′C(ASA)
∴AB′=AB.
作业布置
∠CAB=∠CAB′
∠ACB′=∠ACB
AC=AC.
2.如图,小明家有一个玻璃容器,他想测量一下它的内径是多少,但是他无法将刻度尺伸进容器直接测量,于是他把两根长度相等的小木条AB,CD的中点连在一起,木条可以绕中点O自由转动,这样只要测量A,C的距离,就可以知道玻璃容器的内径,你知道其中的道理吗?请说明理由.
----------------
-------------
3. 如图4-5-17,是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24 cm,CF=3 cm,则制成整个金属框架所需这种材料的总长度为 ( )
A. 45 cm
B. 48 cm
C. 51 cm
D. 54 cm
A
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
