5.2探索轴对称的性质 课件(共30张PPT)
文档属性
| 名称 | 5.2探索轴对称的性质 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 21:16:03 | ||
图片预览



文档简介
数学北师大版
七年级下
5.2 探索轴对称的性质
复习回顾
轴对称图形:如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形。
这条直线叫这个图形的对称轴。
轴对称:对于两个图形,把一个图形沿着某一条直线对折,如果它能够与另一个图形完全重合,那么就说这两个图形成轴对称。
这条直线就是对称轴。
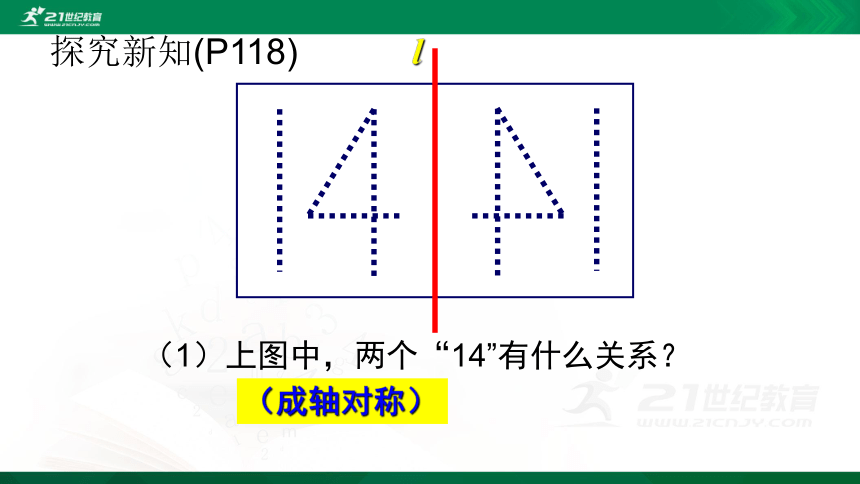
l
(1)上图中,两个“14”有什么关系?
(成轴对称)
探究新知(P118)
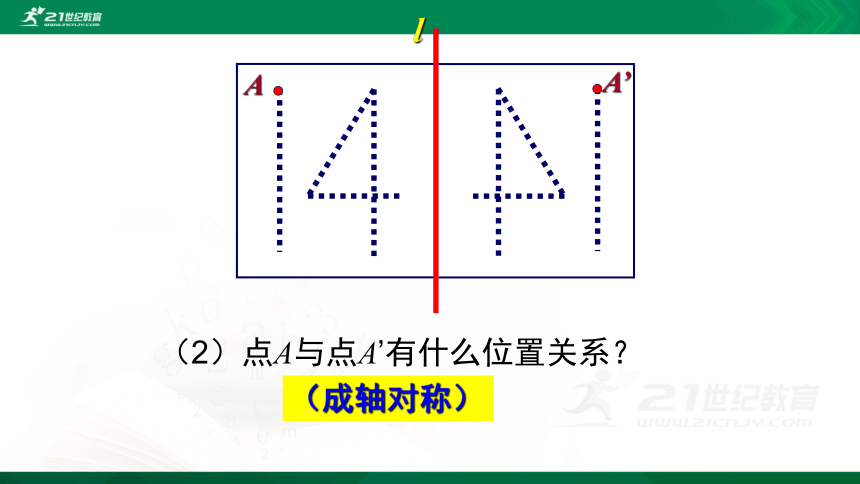
l
A
A’
(2)点A与点A’有什么位置关系?
(成轴对称)
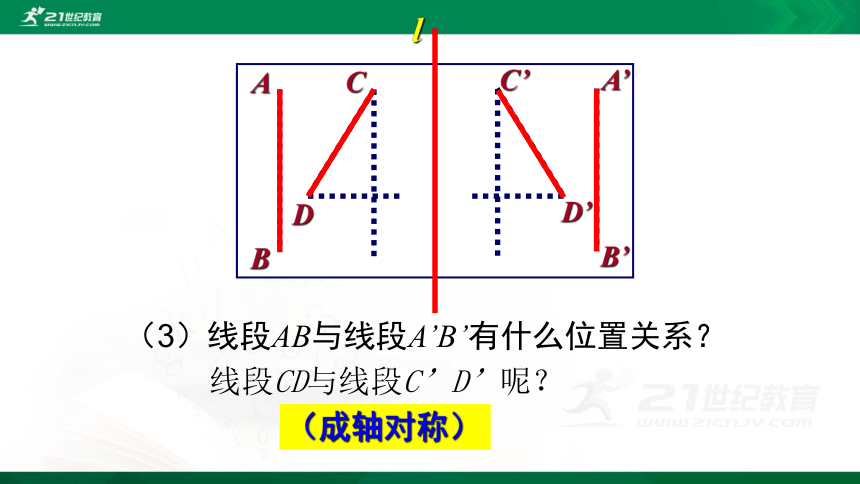
l
(3)线段AB与线段A’B’有什么位置关系?
A
B
A’
B’
线段CD与线段C’D’呢?
C
D
C’
D’
(成轴对称)
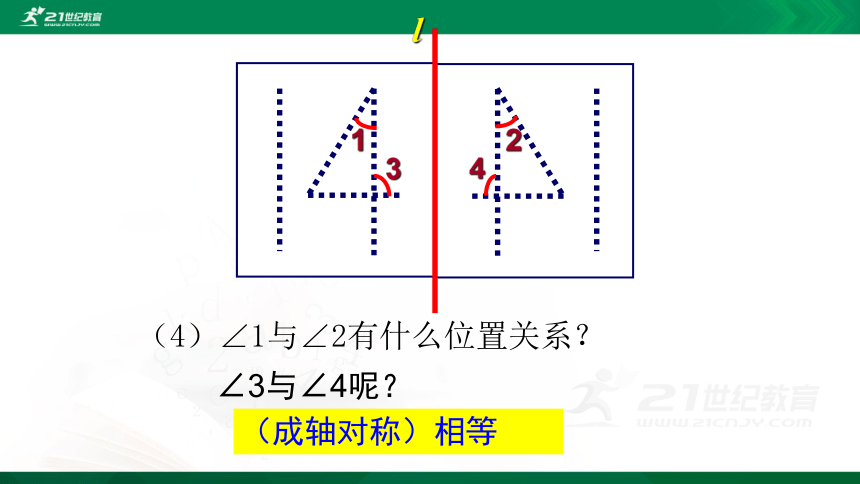
l
(4)∠1与∠2有什么位置关系?
∠3与∠4呢?
1
2
3
4
(成轴对称)相等
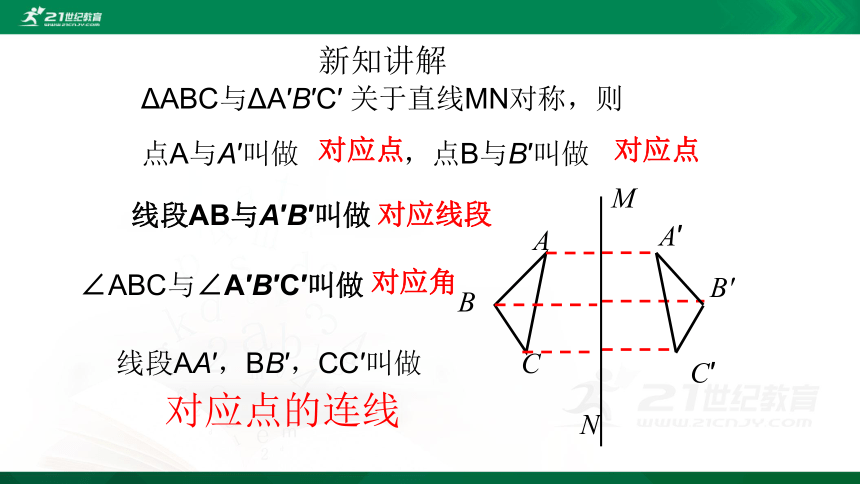
ΔABC与ΔA′B′C′ 关于直线MN对称,则
点A与A′叫做 ,点B与B′叫做
A
A′
C
B
B′
C′
N
M
线段AB与A′B′叫做
对应点
对应点
对应线段
线段AA′,BB′,CC′叫做
对应点的连线
对应角
∠ABC与∠A′B′C′叫做
新知讲解
l
1
2
A
A’
B
B’
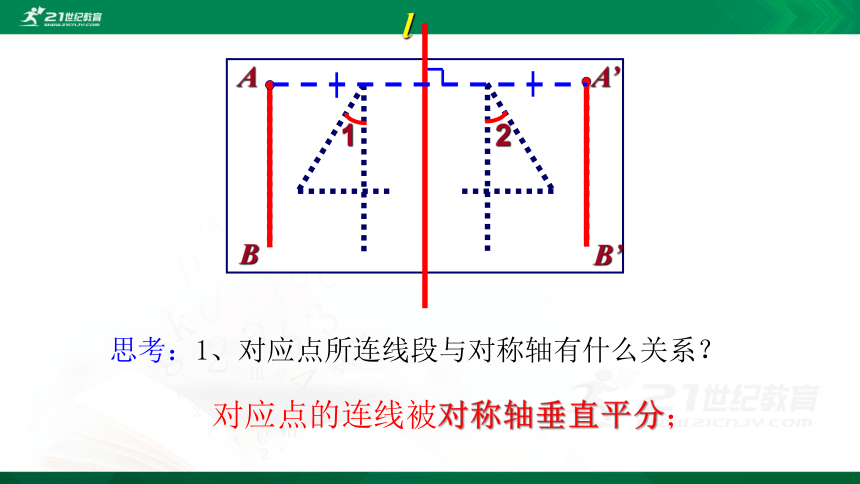
思考:1、对应点所连线段与对称轴有什么关系?
对应点的连线被对称轴垂直平分;
所以 线段OA、OA′重合,
因为 ∠1=∠2 且 ∠1+∠2=180°,
即 O是AA′的中点.
所以 ∠1=∠2=90°.
m
A
A′
●
●
2
o
1
活动
把一张白纸对折,扎一个小孔,记为A,随后展开,另一个点记为A′,连结A和A′两点,观察、分析AA′和折痕m有什么关系?
探究结论:对应点所连接线段被对称轴垂直且平分。
因为 把纸沿折痕 m 折叠时,点A,A′重合,
所以A,Am垂直且平分
l
1
2
A
A’
B
B’
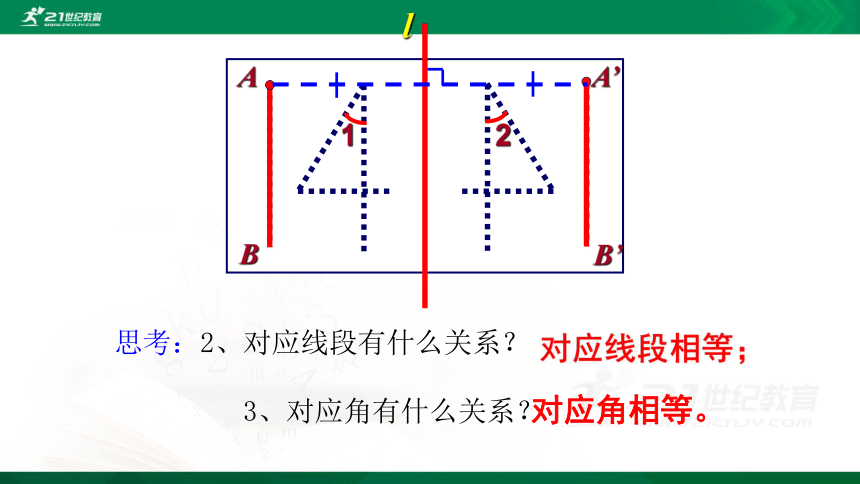
思考:2、对应线段有什么关系?
3、对应角有什么关系?
对应线段相等;
对应角相等。
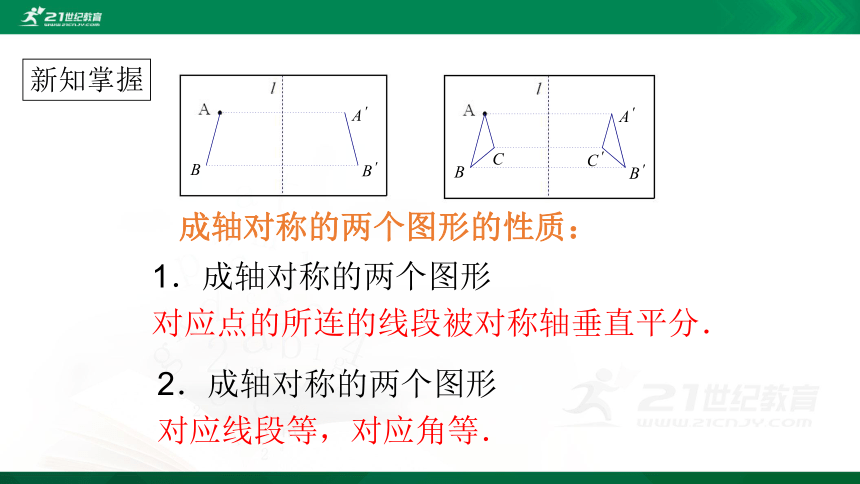
1.成轴对称的两个图形
对应点的所连的线段被对称轴垂直平分.
成轴对称的两个图形的性质:
2.成轴对称的两个图形
对应线段等,对应角等.
新知掌握
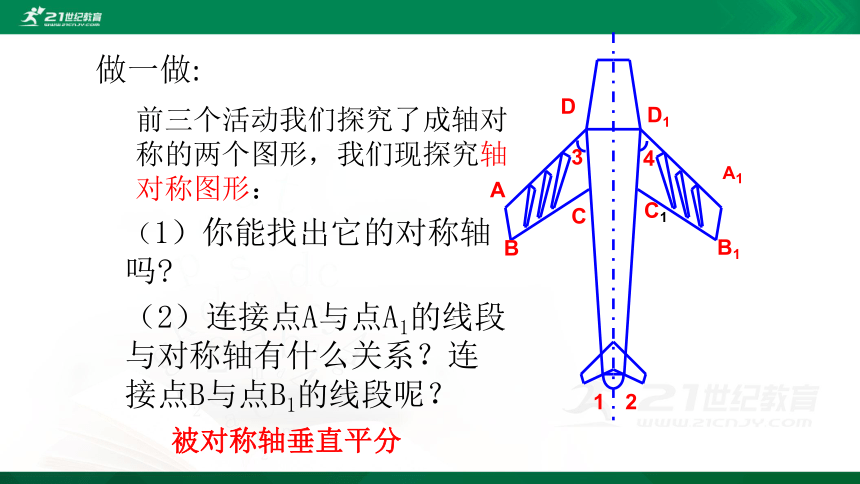
前三个活动我们探究了成轴对称的两个图形,我们现探究轴 对称图形:
(1)你能找出它的对称轴吗?
(2)连接点A与点A1的线段与对称轴有什么关系?连接点B与点B1的线段呢?
B
C
D
D1
C1
B1
3
4
1
2
A
A1
做一做:
被对称轴垂直平分
(3)线段AD与线段A1D1有什么数量关系?线段BC与B1C1呢?为什么?
(4)∠1与∠2有什么关系? ∠ 3与∠4呢?说说你的理由?
B
C
D
D1
C1
B1
3
4
1
2
A
A1
对应线段等,
对应角等
例:已知三角形ABC,作出关于直线a为对称轴的图形
------
------
-----------
-----------
-------
-------
------
------
-----------
-----------
A′
B′
C′
C′
A′
B′
图5-7是一个图案的一半,其中的虚线是这个图案的对称轴,请画出这个图的另一半。
方法:
补全轴对称图形的关键是先找准关键点,过此点作对称轴的垂线段,再延长一倍,得到它的对称点,依此把所有的关键点作出来.再把对应的线段连起来。
做一做:
做一做 图5-7是一个图案的一半,其中的虚线是这个图案的对称轴,画出这个图案的另一半.
方法:
补全轴对称图形的关键是先找准关键点,过此点作对称轴的垂线段,再延长一倍,得到它的对称点,依此把所有的关键点作出来.再把对应的线段连起来。
1.画对称轴
(1)如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.因此,我们只要找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.
(2)对于轴对称图形,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
要点精析:①作对称轴的前提是两个图形成轴对称或一个图形是轴对称图形,否则不能作对称轴;
②对于轴对称图形,由于对称轴不一定唯一,因此要注意选取不同类型的对应点,作出其所有的对称轴.
知识归纳
例1
如图,△ABC和△DEF关于某条直线成轴对称,你能画出这条直线吗?
能.
(1)连接AD;
(2)取AD的中点O,过O作直线MN⊥AD,
则MN即为所求作的直线.如图.
解:
2.画原图关于某直线对称的图形:
(1)依据:如果两个图形关于某一条直线对称,那么连
接任意一组对应点的线段被对称轴垂直平分.
(2)画原图关于某直线对称的图形的步骤:
画原图关于某直线对称的图形要经历一找二作三连
这三个步骤:
①找:在原图形上找特殊点(如线段的端点);
②作:作各个特殊点关于对称轴的对称点;
③连:按原图的顺序连接所作的各对称点.
要点精析:
(1)图形上的特殊点还有角的顶点,图形中边与边的交点等
(2)对称轴上的点的对称点是它本身;
(3)找图形上的特殊点时,要找全,否则画出的对称图形不准确.
(3)画出的新图形与原图形的关系:
①新图形与原图形的形状、大小完全相同;
②新图形上的每一点都是原图形上的某一点关于对
称轴的对称点;
③连接任意一组对应点的线段被对称轴垂直平分.
想想:一次晚会上,主持人出了一道题目:“如何把 变成一个真正的等式?”过了很长时间,也没有人答出。
小兰仅仅拿了一面镜子,就很快解决了这道题目。
你知道她是怎样做的吗?
你知道为什么吗?
1、如图,已知点P 是∠AOB内任意一点,点 P1,P 关于OA对称,点 P2,P 关于OB对称。连接P1P2,分别交OA,OB于C, D。连接PC,PD。若P1P2=10cm,则△PCD的周长为________。
10cm
P
.
.
.
P2
P1
C
D
B
A
O
巩固练习
如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD的大小是( )
A.150° B.300°
C.210° D.330°
例2
B
由轴对称的性质可知:
∠AFC=∠EFC,∠BCF=∠DCF,
∴∠EFC+∠DCF=∠AFC+∠BCF=150°,
∴∠AFE+∠BCD=∠AFC+∠EFC+∠BCF+∠DCF
=150°+150°=300°.
例3
如图,要在公路MN旁修建一个货物中转站,分别向A,B两个开发区运货,若要求货物中转站到A,B两个开发区的距离和最小,那么货物中转站应修建在何处?说明理由.
①作点A关于直线MN的对称点A′;
②连接BA′交MN于点P,则点P就
是货物中转站的位置.如图.
理由:如图,在直线MN上另取一点P′,连接AP,
A′P′,AP′,BP′.因为直线MN是点A,A′的对称轴,
点P,P′在对称轴上,所以PA=PA′,P′A=P′A′.所以
PA+PB=PA′+PB=A′B.在△A′P′B中,因为A′B<
P′A′+P′B,所以PA+PB<P′A′+P′B,即PA+PB<
P′A+P′B,所以PA+PB最小.
解:
练习1:如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)试说明:△FGC≌△EBC;
(2)若AB=8,AD=4,
求四边形ECGF(阴影部分)
的面积.
课外作业
解:(1)由题意知∠BCF=∠ECG=90°,
所以∠GCF+∠FCE=90°,∠FCE+∠BCE=90°,
所以∠GCF=∠BCE.又因为∠G=∠B=90°,
GC=BC,所以△FGC≌△EBC. (2)由(1)知,DF=GF=BE,
所以四边形ECGF的面积=四边形AEFD的面积
=四边形EBCF的面积= 四边形ABCD的面积
= ×8×4=16.
2:如图所示,AD为 △ABC 的高,∠B= 2∠C ,借助于轴对称的性质想一想:CD与AB+BD相等吗?请说明你的理由.
答:相等,理由如下:
在DC上截取DE使DE=DB,连接AE
∵AD⊥BE且DB=DE ∴B、E关于AD对称
∴△ABD与△AED关于直线AD对称
∴ △ABD ≌ △AED ∴AB=AE,∠AED= ∠B
又∵ ∠B=2 ∠C ∴ ∠AED= 2 ∠C
而∠AED= ∠C + ∠CAE ∴ ∠CAE = ∠ C
∴AE=CE ∴AB=CE 故AB+BD=DE+EC
即:AB+BD=CD
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
七年级下
5.2 探索轴对称的性质
复习回顾
轴对称图形:如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形。
这条直线叫这个图形的对称轴。
轴对称:对于两个图形,把一个图形沿着某一条直线对折,如果它能够与另一个图形完全重合,那么就说这两个图形成轴对称。
这条直线就是对称轴。
l
(1)上图中,两个“14”有什么关系?
(成轴对称)
探究新知(P118)
l
A
A’
(2)点A与点A’有什么位置关系?
(成轴对称)
l
(3)线段AB与线段A’B’有什么位置关系?
A
B
A’
B’
线段CD与线段C’D’呢?
C
D
C’
D’
(成轴对称)
l
(4)∠1与∠2有什么位置关系?
∠3与∠4呢?
1
2
3
4
(成轴对称)相等
ΔABC与ΔA′B′C′ 关于直线MN对称,则
点A与A′叫做 ,点B与B′叫做
A
A′
C
B
B′
C′
N
M
线段AB与A′B′叫做
对应点
对应点
对应线段
线段AA′,BB′,CC′叫做
对应点的连线
对应角
∠ABC与∠A′B′C′叫做
新知讲解
l
1
2
A
A’
B
B’
思考:1、对应点所连线段与对称轴有什么关系?
对应点的连线被对称轴垂直平分;
所以 线段OA、OA′重合,
因为 ∠1=∠2 且 ∠1+∠2=180°,
即 O是AA′的中点.
所以 ∠1=∠2=90°.
m
A
A′
●
●
2
o
1
活动
把一张白纸对折,扎一个小孔,记为A,随后展开,另一个点记为A′,连结A和A′两点,观察、分析AA′和折痕m有什么关系?
探究结论:对应点所连接线段被对称轴垂直且平分。
因为 把纸沿折痕 m 折叠时,点A,A′重合,
所以A,Am垂直且平分
l
1
2
A
A’
B
B’
思考:2、对应线段有什么关系?
3、对应角有什么关系?
对应线段相等;
对应角相等。
1.成轴对称的两个图形
对应点的所连的线段被对称轴垂直平分.
成轴对称的两个图形的性质:
2.成轴对称的两个图形
对应线段等,对应角等.
新知掌握
前三个活动我们探究了成轴对称的两个图形,我们现探究轴 对称图形:
(1)你能找出它的对称轴吗?
(2)连接点A与点A1的线段与对称轴有什么关系?连接点B与点B1的线段呢?
B
C
D
D1
C1
B1
3
4
1
2
A
A1
做一做:
被对称轴垂直平分
(3)线段AD与线段A1D1有什么数量关系?线段BC与B1C1呢?为什么?
(4)∠1与∠2有什么关系? ∠ 3与∠4呢?说说你的理由?
B
C
D
D1
C1
B1
3
4
1
2
A
A1
对应线段等,
对应角等
例:已知三角形ABC,作出关于直线a为对称轴的图形
------
------
-----------
-----------
-------
-------
------
------
-----------
-----------
A′
B′
C′
C′
A′
B′
图5-7是一个图案的一半,其中的虚线是这个图案的对称轴,请画出这个图的另一半。
方法:
补全轴对称图形的关键是先找准关键点,过此点作对称轴的垂线段,再延长一倍,得到它的对称点,依此把所有的关键点作出来.再把对应的线段连起来。
做一做:
做一做 图5-7是一个图案的一半,其中的虚线是这个图案的对称轴,画出这个图案的另一半.
方法:
补全轴对称图形的关键是先找准关键点,过此点作对称轴的垂线段,再延长一倍,得到它的对称点,依此把所有的关键点作出来.再把对应的线段连起来。
1.画对称轴
(1)如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.因此,我们只要找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.
(2)对于轴对称图形,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴.
要点精析:①作对称轴的前提是两个图形成轴对称或一个图形是轴对称图形,否则不能作对称轴;
②对于轴对称图形,由于对称轴不一定唯一,因此要注意选取不同类型的对应点,作出其所有的对称轴.
知识归纳
例1
如图,△ABC和△DEF关于某条直线成轴对称,你能画出这条直线吗?
能.
(1)连接AD;
(2)取AD的中点O,过O作直线MN⊥AD,
则MN即为所求作的直线.如图.
解:
2.画原图关于某直线对称的图形:
(1)依据:如果两个图形关于某一条直线对称,那么连
接任意一组对应点的线段被对称轴垂直平分.
(2)画原图关于某直线对称的图形的步骤:
画原图关于某直线对称的图形要经历一找二作三连
这三个步骤:
①找:在原图形上找特殊点(如线段的端点);
②作:作各个特殊点关于对称轴的对称点;
③连:按原图的顺序连接所作的各对称点.
要点精析:
(1)图形上的特殊点还有角的顶点,图形中边与边的交点等
(2)对称轴上的点的对称点是它本身;
(3)找图形上的特殊点时,要找全,否则画出的对称图形不准确.
(3)画出的新图形与原图形的关系:
①新图形与原图形的形状、大小完全相同;
②新图形上的每一点都是原图形上的某一点关于对
称轴的对称点;
③连接任意一组对应点的线段被对称轴垂直平分.
想想:一次晚会上,主持人出了一道题目:“如何把 变成一个真正的等式?”过了很长时间,也没有人答出。
小兰仅仅拿了一面镜子,就很快解决了这道题目。
你知道她是怎样做的吗?
你知道为什么吗?
1、如图,已知点P 是∠AOB内任意一点,点 P1,P 关于OA对称,点 P2,P 关于OB对称。连接P1P2,分别交OA,OB于C, D。连接PC,PD。若P1P2=10cm,则△PCD的周长为________。
10cm
P
.
.
.
P2
P1
C
D
B
A
O
巩固练习
如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD的大小是( )
A.150° B.300°
C.210° D.330°
例2
B
由轴对称的性质可知:
∠AFC=∠EFC,∠BCF=∠DCF,
∴∠EFC+∠DCF=∠AFC+∠BCF=150°,
∴∠AFE+∠BCD=∠AFC+∠EFC+∠BCF+∠DCF
=150°+150°=300°.
例3
如图,要在公路MN旁修建一个货物中转站,分别向A,B两个开发区运货,若要求货物中转站到A,B两个开发区的距离和最小,那么货物中转站应修建在何处?说明理由.
①作点A关于直线MN的对称点A′;
②连接BA′交MN于点P,则点P就
是货物中转站的位置.如图.
理由:如图,在直线MN上另取一点P′,连接AP,
A′P′,AP′,BP′.因为直线MN是点A,A′的对称轴,
点P,P′在对称轴上,所以PA=PA′,P′A=P′A′.所以
PA+PB=PA′+PB=A′B.在△A′P′B中,因为A′B<
P′A′+P′B,所以PA+PB<P′A′+P′B,即PA+PB<
P′A+P′B,所以PA+PB最小.
解:
练习1:如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)试说明:△FGC≌△EBC;
(2)若AB=8,AD=4,
求四边形ECGF(阴影部分)
的面积.
课外作业
解:(1)由题意知∠BCF=∠ECG=90°,
所以∠GCF+∠FCE=90°,∠FCE+∠BCE=90°,
所以∠GCF=∠BCE.又因为∠G=∠B=90°,
GC=BC,所以△FGC≌△EBC. (2)由(1)知,DF=GF=BE,
所以四边形ECGF的面积=四边形AEFD的面积
=四边形EBCF的面积= 四边形ABCD的面积
= ×8×4=16.
2:如图所示,AD为 △ABC 的高,∠B= 2∠C ,借助于轴对称的性质想一想:CD与AB+BD相等吗?请说明你的理由.
答:相等,理由如下:
在DC上截取DE使DE=DB,连接AE
∵AD⊥BE且DB=DE ∴B、E关于AD对称
∴△ABD与△AED关于直线AD对称
∴ △ABD ≌ △AED ∴AB=AE,∠AED= ∠B
又∵ ∠B=2 ∠C ∴ ∠AED= 2 ∠C
而∠AED= ∠C + ∠CAE ∴ ∠CAE = ∠ C
∴AE=CE ∴AB=CE 故AB+BD=DE+EC
即:AB+BD=CD
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
