青岛版数学八年级下册第一次月考测试题(word版含答案)
文档属性
| 名称 | 青岛版数学八年级下册第一次月考测试题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 181.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 17:46:34 | ||
图片预览


文档简介
青岛版数学八年级下册第一次月考测试题及答案解析
(根据第六单元和第七单元编写)
一、选择题
1.已知?ABCD的周长为32,AB=4,则BC等于(??
)
A.?4?????????????????????????????????????????B.?12?????????????????????????????????????????C.?24?????????????????????????????????????????D.?28
2.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.?选①②???????????????????????????????B.?选①③??????????????????????????C.?选②④??????????????????????????????D.?选②③
3.下列条件中,不能判定四边形是平行四边形的是(?
)
A.?两组对边分别平行??????????????????????????????????????????????B.?一组对边平行,另一组对边相等
C.?两组对边分别相等??????????????????????????????????????????????D.?一组对边平行且相等
4.如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( )
①BE=CF
②AE是∠DAB的角平分线
③∠DAE+∠DCF=120°.
?
A.?①????????????????????????????????B.?①②???????????????????????????????C.?①②③?????????????D.?都不正确
5.如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2,
则DC和EF的大小关系是( )
A.?DC>EF???????????????????????????B.?DC<EF????????????????????????????C.?DC=EF????????????????????????????D.?无法比较
6.如图,在梯形ABCD中,∠ABC=90?,AE∥CD交BC于E,O是AC的中点,AB=,AD=2,BC=3,下列结论:
①∠CAE=30?;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正确的是()
?
A.?①②③?????????????????????????B.?②③④???????????????????????C.?①③④?????????????????????D.?①②③④
7.下列说法中,不正确的是(
).
A
3是的算术平方根
B±3是的平方根
C
-3是的算术平方根
D.-3是的立方根
8.
在-1.414,
HYPERLINK
"http://www./"
EMBED
Equation.3
,π,3.14,2+,3.212212221…,这些数中,无理数的个数为(
).
A.5
B.2
C.3
D.4
9.
已知下列结论:①在数轴上的点只能表示无理数;②任何一个无理数都能用数轴上的点表示;③实数与数轴上的点一一对应;④有理数有无限个,无理数有有限个.其中正确的结论是(
).
A.①②
B.②③
C.③④
D.②③④
10.
若,,则(
)
A.8
B.±8
C.±2
D.±8或±2
11.
已知一个直角三角形的两边长分别为3和4,则第三边长是( )
A.5
B.25
C.
D.5或
12.
若a、b为实数,且满足│a-2│+=0,则b-a的值为(
)
A.2
B.0
C.-2
D.以上都不对
二、填空题
13.矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC+BD=16,则该矩形的面积为________
14.如图,剪两张等宽对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是________.
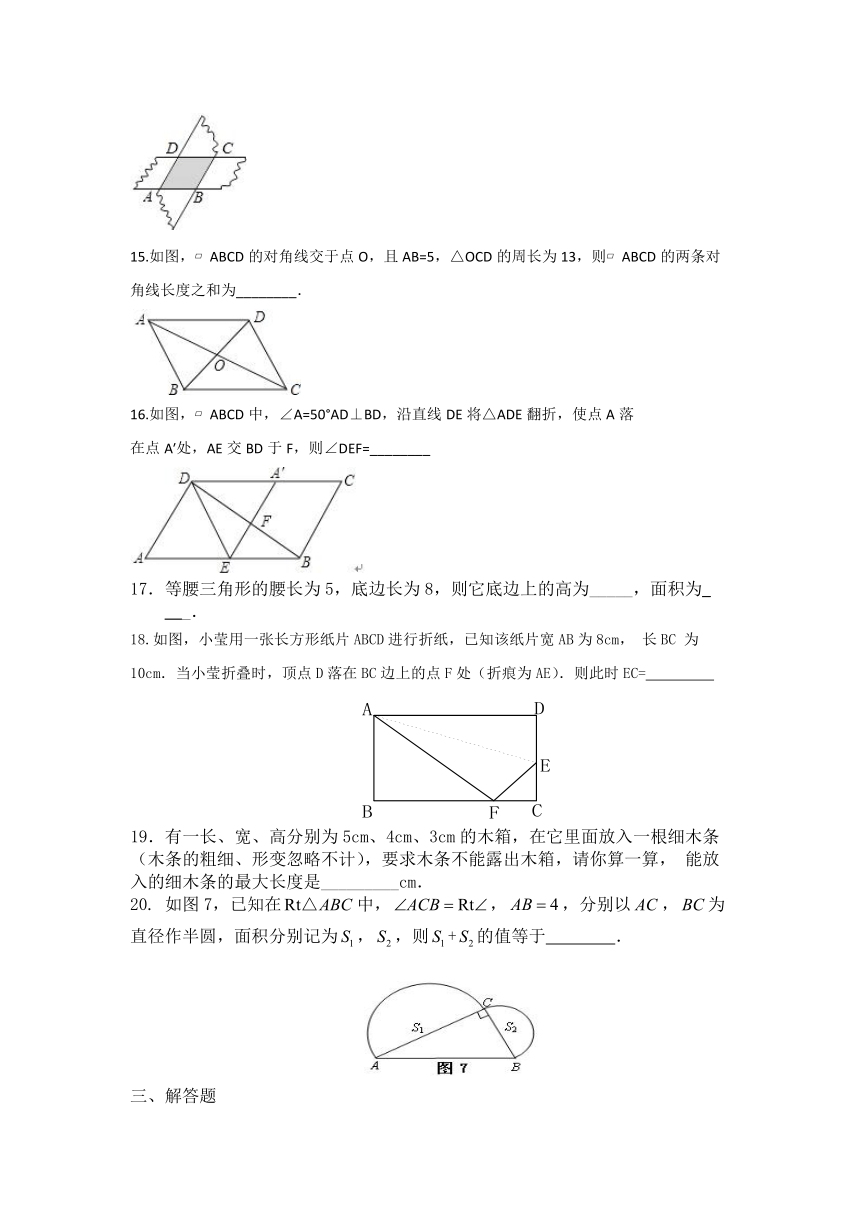
15.如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为13,则?ABCD的两条对角线长度之和为________.
16.如图,?ABCD中,∠A=50°AD⊥BD,沿直线DE将△ADE翻折,使点A落
在点A′处,AE交BD于F,则∠DEF=________?
17.等腰三角形的腰长为5,底边长为8,则它底边上的高为_____,面积为_
___.
18.如图,小莹用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小莹折叠时,顶点D落在BC边上的点F处(折痕为AE).则此时EC=
19.有一长、宽、高分别为5cm、4cm、3cm的木箱,在它里面放入一根细木条(木条的粗细、形变忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是_________cm.
20.
如图7,已知在中,,,分别以,为直径作半圆,面积分别记为,,则+的值等于
.
三、解答题
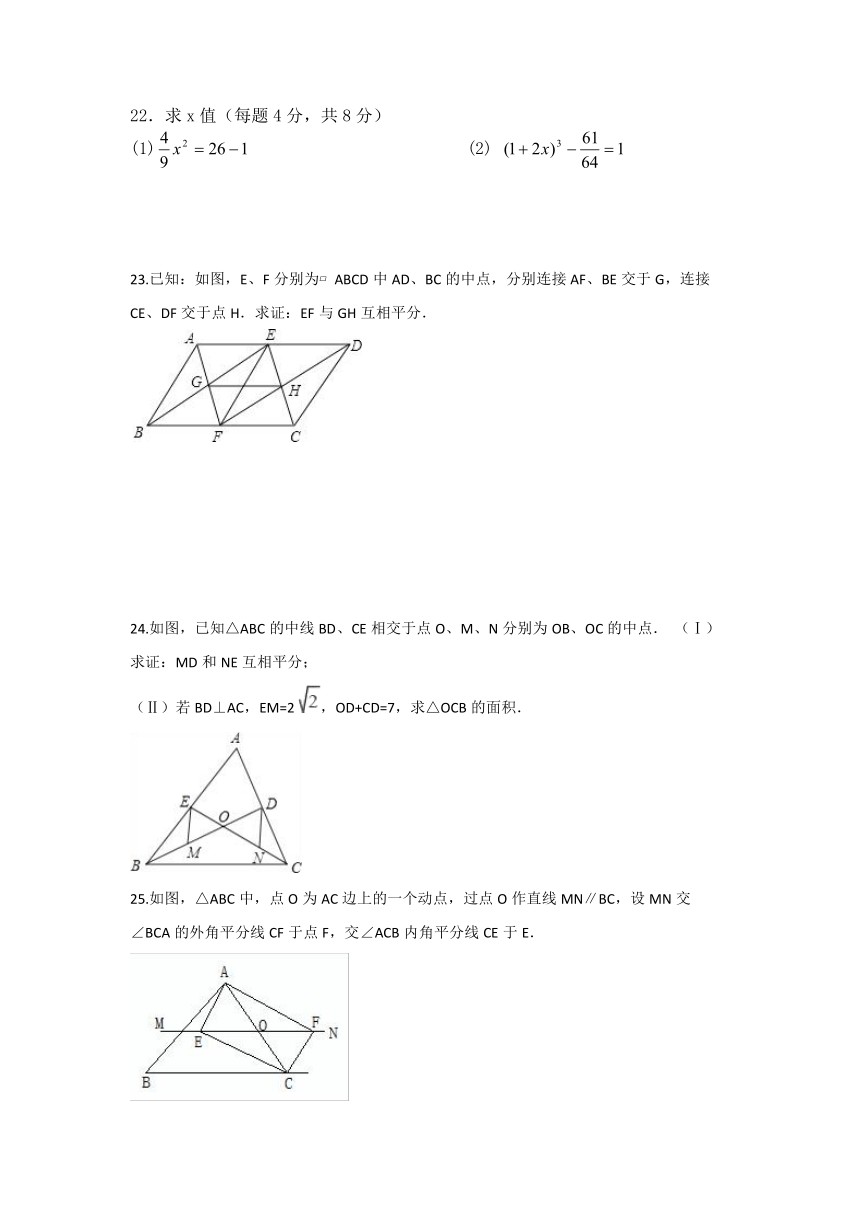
22.求x值(每题4分,共8分)
(1)
(2)
23.已知:如图,E、F分别为?ABCD中AD、BC的中点,分别连接AF、BE交于G,连接CE、DF交于点H.求证:EF与GH互相平分.
24.如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.
(Ⅰ)求证:MD和NE互相平分;
(Ⅱ)若BD⊥AC,EM=2
,OD+CD=7,求△OCB的面积.
25.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论
。
26.请在同一个数轴上用尺规作出
和
的对应的点.
27.一个直角三角形的两边m、n恰好满足等式m-+=8,求第三条边的长.
28.
如图,铁路上A、B两点相距25km,
C、D为两村庄,若DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.
求E应建在距A多远处?
29.
已知正方形ABCD的边长为4,E为AB中点,F为A上的一点,且AF=AD。
试判断△EFC的形状.
并说明理由
答案解析
一、1-
6
B
D
B
C
C
D
7-12
C
D
B
D
C
C
二、13.
16
14.
菱形
15.
16
16.
65°
17.3,12
18.3
cm
19.
5
20.2π
三、22.(1)x=±7.5
(2)x=1/8
23.
证明:∵E为AD的中点,F为BC的中点,
∴AE=
AD,CF=
BC,
∵四边形ABCD是平行四边形,
∴AD∥BC,∴AE∥CF,AE=CF,
∴四边形AFCE是平行四边形,
∴AF∥CE,
同理可证:BE∥DF,
∴四边形GFHE是平行四边形,
∴EF与GH互相平分
24.
(Ⅰ)证明:连接ED、MN,∵CE、BD是△ABC的中线,
∴E、D是AB、AC中点,
∴ED∥BC,ED=
BC,
∵M、N分别为OB、OC的中点,
∴MN∥BC,MN=
BC,
∴ED∥MN,ED=MN,
∴四边形DEMN是平行四边形,
∴MD和NE互相平分;
(Ⅱ)解:由(Ⅰ)可得DN=EM=2
,
∵BD⊥AC,
∴∠ODC=90°,
∵N是OC的中点,
∴OC=2DN=4
(直角三角形斜边中线等于斜边的一半)
∵OD2+CD2=OC2=32,
(OD+CD)2=OD2+CD2+2OD×CD=72=49,
2OD×CD=49﹣32=17,
OD×CD=8.5,
∵OB=2OM=2OD,
∴S△OCB=
OB×CD=OD×CD=8.5.
25.
解:(1)∵CE平分∠ACB,
∴∠ACE=∠BCE,
∵MN∥BC,
∴∠OEC=∠ECB,
∴∠OEC=∠OCE,
∴OE=OC,
同理,OC=OF,
∴OE=OF;
(2)当点O运动到AC中点处时,四边形AECF是矩形.
如图AO=CO,EO=FO,
∴四边形AECF为平行四边形,
∵CE平分∠ACB,
∴∠ACE=∠ACB,
同理,∠ACF=∠ACG,
∴∠ECF=∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°,
∴四边形AECF是矩形;
(3)△ABC是直角三角形
∵四边形AECF是正方形,
∴AC⊥EN,故∠AOM=90°,
∵MN∥BC,
∴∠BCA=∠AOM,
∴∠BCA=90°,
∴△ABC是直角三角形.
26.略
27.由已知,得2n-12=12-2n=0.
∴
n=6
,
m=8
∴第三边的长为10
28.设E应建在距A地x
km,处,根据勾股定理得
102+x2=(25-x)2+152
解得x=15
29.
△EFC为直角三角形。
根据勾股定理计算得:EF2=5,EC2=20,CF2=25
∵EF2+
EC2=
CF2
∴△EFC为直角三角形
C
A
B
D
E
10
15
(根据第六单元和第七单元编写)
一、选择题
1.已知?ABCD的周长为32,AB=4,则BC等于(??
)
A.?4?????????????????????????????????????????B.?12?????????????????????????????????????????C.?24?????????????????????????????????????????D.?28
2.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )
A.?选①②???????????????????????????????B.?选①③??????????????????????????C.?选②④??????????????????????????????D.?选②③
3.下列条件中,不能判定四边形是平行四边形的是(?
)
A.?两组对边分别平行??????????????????????????????????????????????B.?一组对边平行,另一组对边相等
C.?两组对边分别相等??????????????????????????????????????????????D.?一组对边平行且相等
4.如图所示,在平行四边形ABCD中,∠ABE=∠AEB,AE∥DF,DC是∠ADF的角平分线.下列说法正确的是( )
①BE=CF
②AE是∠DAB的角平分线
③∠DAE+∠DCF=120°.
?
A.?①????????????????????????????????B.?①②???????????????????????????????C.?①②③?????????????D.?都不正确
5.如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,AB=2,
则DC和EF的大小关系是( )
A.?DC>EF???????????????????????????B.?DC<EF????????????????????????????C.?DC=EF????????????????????????????D.?无法比较
6.如图,在梯形ABCD中,∠ABC=90?,AE∥CD交BC于E,O是AC的中点,AB=,AD=2,BC=3,下列结论:
①∠CAE=30?;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正确的是()
?
A.?①②③?????????????????????????B.?②③④???????????????????????C.?①③④?????????????????????D.?①②③④
7.下列说法中,不正确的是(
).
A
3是的算术平方根
B±3是的平方根
C
-3是的算术平方根
D.-3是的立方根
8.
在-1.414,
HYPERLINK
"http://www./"
EMBED
Equation.3
,π,3.14,2+,3.212212221…,这些数中,无理数的个数为(
).
A.5
B.2
C.3
D.4
9.
已知下列结论:①在数轴上的点只能表示无理数;②任何一个无理数都能用数轴上的点表示;③实数与数轴上的点一一对应;④有理数有无限个,无理数有有限个.其中正确的结论是(
).
A.①②
B.②③
C.③④
D.②③④
10.
若,,则(
)
A.8
B.±8
C.±2
D.±8或±2
11.
已知一个直角三角形的两边长分别为3和4,则第三边长是( )
A.5
B.25
C.
D.5或
12.
若a、b为实数,且满足│a-2│+=0,则b-a的值为(
)
A.2
B.0
C.-2
D.以上都不对
二、填空题
13.矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AC+BD=16,则该矩形的面积为________
14.如图,剪两张等宽对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是________.
15.如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为13,则?ABCD的两条对角线长度之和为________.
16.如图,?ABCD中,∠A=50°AD⊥BD,沿直线DE将△ADE翻折,使点A落
在点A′处,AE交BD于F,则∠DEF=________?
17.等腰三角形的腰长为5,底边长为8,则它底边上的高为_____,面积为_
___.
18.如图,小莹用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小莹折叠时,顶点D落在BC边上的点F处(折痕为AE).则此时EC=
19.有一长、宽、高分别为5cm、4cm、3cm的木箱,在它里面放入一根细木条(木条的粗细、形变忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是_________cm.
20.
如图7,已知在中,,,分别以,为直径作半圆,面积分别记为,,则+的值等于
.
三、解答题
22.求x值(每题4分,共8分)
(1)
(2)
23.已知:如图,E、F分别为?ABCD中AD、BC的中点,分别连接AF、BE交于G,连接CE、DF交于点H.求证:EF与GH互相平分.
24.如图,已知△ABC的中线BD、CE相交于点O、M、N分别为OB、OC的中点.
(Ⅰ)求证:MD和NE互相平分;
(Ⅱ)若BD⊥AC,EM=2
,OD+CD=7,求△OCB的面积.
25.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论
。
26.请在同一个数轴上用尺规作出
和
的对应的点.
27.一个直角三角形的两边m、n恰好满足等式m-+=8,求第三条边的长.
28.
如图,铁路上A、B两点相距25km,
C、D为两村庄,若DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.
求E应建在距A多远处?
29.
已知正方形ABCD的边长为4,E为AB中点,F为A上的一点,且AF=AD。
试判断△EFC的形状.
并说明理由
答案解析
一、1-
6
B
D
B
C
C
D
7-12
C
D
B
D
C
C
二、13.
16
14.
菱形
15.
16
16.
65°
17.3,12
18.3
cm
19.
5
20.2π
三、22.(1)x=±7.5
(2)x=1/8
23.
证明:∵E为AD的中点,F为BC的中点,
∴AE=
AD,CF=
BC,
∵四边形ABCD是平行四边形,
∴AD∥BC,∴AE∥CF,AE=CF,
∴四边形AFCE是平行四边形,
∴AF∥CE,
同理可证:BE∥DF,
∴四边形GFHE是平行四边形,
∴EF与GH互相平分
24.
(Ⅰ)证明:连接ED、MN,∵CE、BD是△ABC的中线,
∴E、D是AB、AC中点,
∴ED∥BC,ED=
BC,
∵M、N分别为OB、OC的中点,
∴MN∥BC,MN=
BC,
∴ED∥MN,ED=MN,
∴四边形DEMN是平行四边形,
∴MD和NE互相平分;
(Ⅱ)解:由(Ⅰ)可得DN=EM=2
,
∵BD⊥AC,
∴∠ODC=90°,
∵N是OC的中点,
∴OC=2DN=4
(直角三角形斜边中线等于斜边的一半)
∵OD2+CD2=OC2=32,
(OD+CD)2=OD2+CD2+2OD×CD=72=49,
2OD×CD=49﹣32=17,
OD×CD=8.5,
∵OB=2OM=2OD,
∴S△OCB=
OB×CD=OD×CD=8.5.
25.
解:(1)∵CE平分∠ACB,
∴∠ACE=∠BCE,
∵MN∥BC,
∴∠OEC=∠ECB,
∴∠OEC=∠OCE,
∴OE=OC,
同理,OC=OF,
∴OE=OF;
(2)当点O运动到AC中点处时,四边形AECF是矩形.
如图AO=CO,EO=FO,
∴四边形AECF为平行四边形,
∵CE平分∠ACB,
∴∠ACE=∠ACB,
同理,∠ACF=∠ACG,
∴∠ECF=∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°,
∴四边形AECF是矩形;
(3)△ABC是直角三角形
∵四边形AECF是正方形,
∴AC⊥EN,故∠AOM=90°,
∵MN∥BC,
∴∠BCA=∠AOM,
∴∠BCA=90°,
∴△ABC是直角三角形.
26.略
27.由已知,得2n-12=12-2n=0.
∴
n=6
,
m=8
∴第三边的长为10
28.设E应建在距A地x
km,处,根据勾股定理得
102+x2=(25-x)2+152
解得x=15
29.
△EFC为直角三角形。
根据勾股定理计算得:EF2=5,EC2=20,CF2=25
∵EF2+
EC2=
CF2
∴△EFC为直角三角形
C
A
B
D
E
10
15
同课章节目录
