2020-2021学年人教版数 学七年级下册5.3.1平行线的性质 课件(17张)
文档属性
| 名称 | 2020-2021学年人教版数 学七年级下册5.3.1平行线的性质 课件(17张) |  | |
| 格式 | ppt | ||
| 文件大小 | 250.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-13 19:47:05 | ||
图片预览



文档简介
5.3.1 平行线的性质
用直尺和三角板画出两条平行线a、b,再画一条截线c 与直线a、b相交,标出所形成的八个角。
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
测量这些角的度数,把结果填入下表。
再任意画一条截线d,同样度量并比较各对同位角的度数,你的猜想还成立吗?
你还有其他方法验证你的猜想吗?
动手实践,探究新知
c
a
b
a
b
c
如果两直线不平行,上述结论还成立吗?
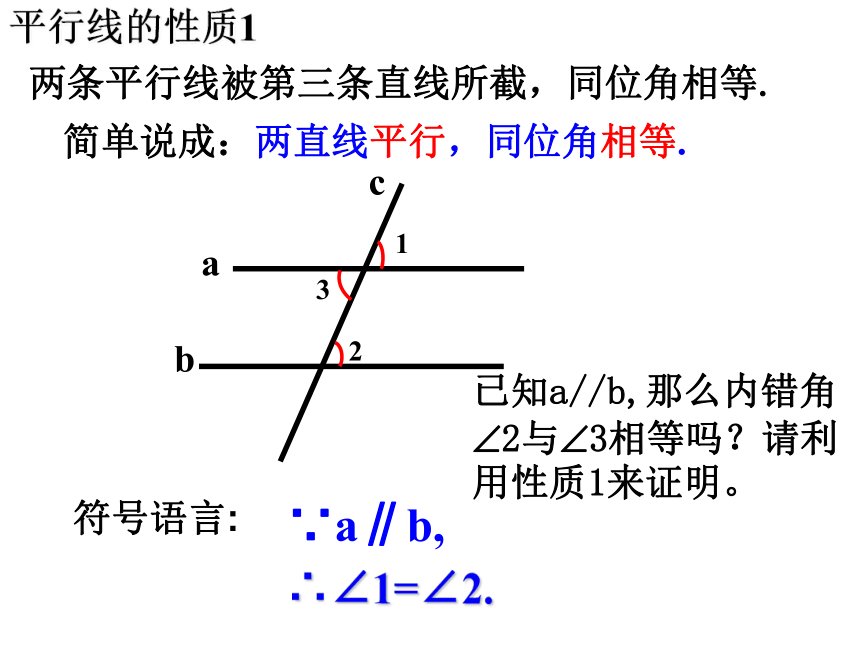
简单说成:两直线平行,同位角相等.
平行线的性质1
两条平行线被第三条直线所截,同位角相等.
∴∠1=∠2.
∵a∥b,
符号语言:
b
1
2
a
c
3
已知a//b,那么内错角
?2与?3相等吗?请利
用性质1来证明。
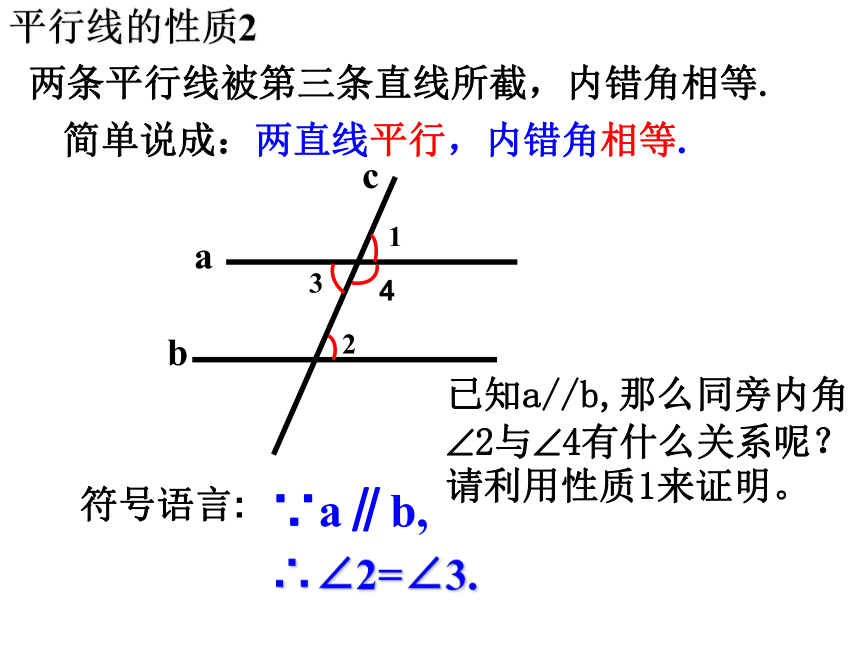
简单说成:两直线平行,内错角相等.
平行线的性质2
两条平行线被第三条直线所截,内错角相等.
∴∠2=∠3.
∵a∥b,
符号语言:
b
1
2
a
c
3
4
已知a//b,那么同旁内角
?2与?4有什么关系呢?
请利用性质1来证明。
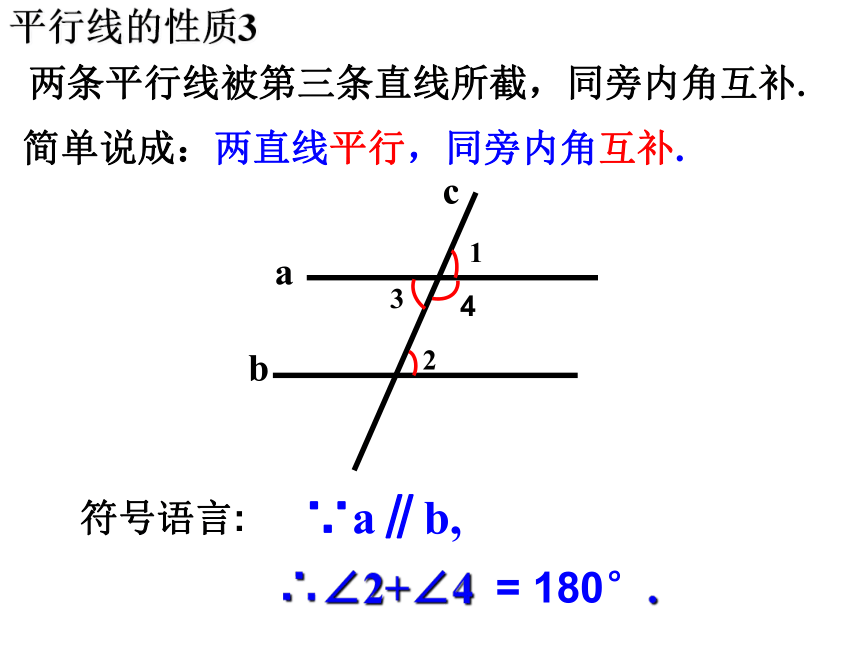
简单说成:两直线平行,同旁内角互补.
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补.
∴∠2+∠4 = 180°.
∵a∥b,
符号语言:
b
1
2
a
c
3
4
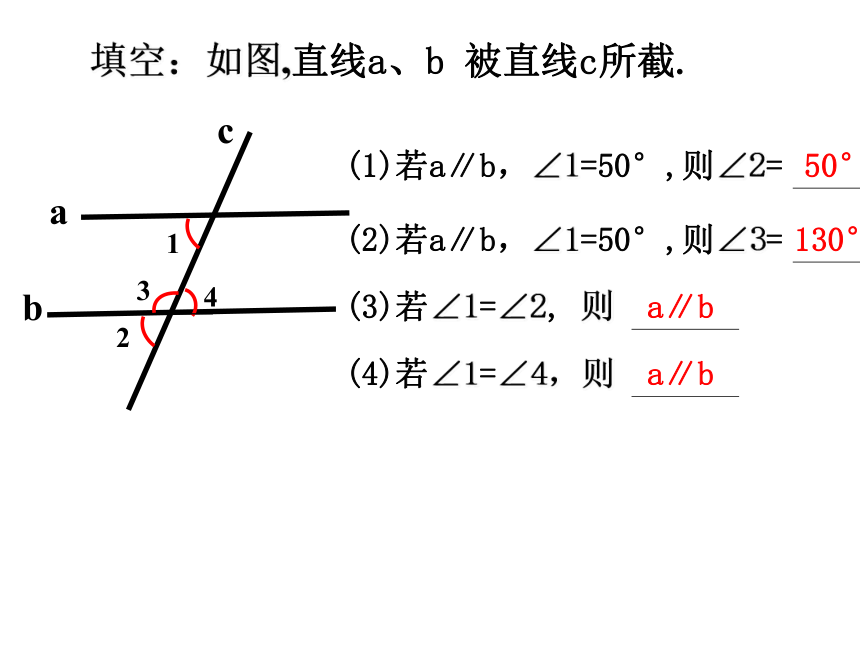
填空:如图,直线a、b 被直线c所截.
b
4
2
a
c
3
1
(1)若a∥b,∠1=50°,则∠2=
(2)若a∥b,∠1=50°,则∠3=
(3)若∠1=∠2, 则
(4)若∠1=∠4,则
50°
a∥b
130°
a∥b
两直线平行
同位角相等
内错角相等
同旁内角互补
两直线的位置关系
两角的数量关系
性质
两角的数量关系
两直线的位置关系
判定
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
例1 如图所示是一块梯形铁片的残余部分,量得∠A=100?,∠B=115°,梯形另外两个角各是多少度?
解:∵梯形上、下两底互相平行,
所以梯形的另外两个角分别是80°, 65°.
由图知 AB∥CD,
∴∠A+∠D=180°,
∠B+∠C=180°(两直线平行,同旁内角互补).
∴ ∠D=180°-∠A=180°-100°= 80°,
∠C=180°-∠B=180°-115°= 65°.
巩固新知,深化理解
1.如图,平行线AB,CD被直线AE所截, 已知∠1=110?,求∠2、 ∠3 、 ∠4的度数。
2. 如图,已知AB∥CD,AE∥CF,∠A=39°,
∠C是多少度?为什么?
巩固新知,深化理解
例2 如图,BCD是一条直线,∠A=75°,∠1=55°,∠2=75°,求∠B的度数.
解:∵ ∠A=∠2=75°(已知)
∴ AB∥CE (内错角相等,两直线平行)
∴ ∠B=∠1(两直线平行,同位角相等)
∵ ∠1=55°(已知)
∴ ∠B=55° (等量代换)
综合运用,熟练技能
解:∵AB//CD (已知)
∴∠C= ( )
又∵∠A=∠C(已知)
∴∠A= ( )
∴ // ( )
∴∠E=∠F ( )
A
D
E
C
B
F
两直线平行,同位角相等
等量代换
内错角相等,两直线平行
两直线平行,内错角相等
3. 完成下面的证明
如图,已知AB//CD,∠A=∠C,求证∠E=∠F .
综合运用,熟练技能
∠ABF
∠ABF
AE
FC
归纳小结
回顾本节课所学主要内容,你有什么收获?
能力拓展:如图,已知∠BAP与∠APD互补,∠1=∠2,求证:∠E=∠F
A
B
C
D
E
F
P
1
2
作业
必做题:课本习题5.3
第1、4、6、14 题
选做题:完成学案上能力拓展题
谢谢各位专家同仁莅临指导!
用直尺和三角板画出两条平行线a、b,再画一条截线c 与直线a、b相交,标出所形成的八个角。
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
测量这些角的度数,把结果填入下表。
再任意画一条截线d,同样度量并比较各对同位角的度数,你的猜想还成立吗?
你还有其他方法验证你的猜想吗?
动手实践,探究新知
c
a
b
a
b
c
如果两直线不平行,上述结论还成立吗?
简单说成:两直线平行,同位角相等.
平行线的性质1
两条平行线被第三条直线所截,同位角相等.
∴∠1=∠2.
∵a∥b,
符号语言:
b
1
2
a
c
3
已知a//b,那么内错角
?2与?3相等吗?请利
用性质1来证明。
简单说成:两直线平行,内错角相等.
平行线的性质2
两条平行线被第三条直线所截,内错角相等.
∴∠2=∠3.
∵a∥b,
符号语言:
b
1
2
a
c
3
4
已知a//b,那么同旁内角
?2与?4有什么关系呢?
请利用性质1来证明。
简单说成:两直线平行,同旁内角互补.
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补.
∴∠2+∠4 = 180°.
∵a∥b,
符号语言:
b
1
2
a
c
3
4
填空:如图,直线a、b 被直线c所截.
b
4
2
a
c
3
1
(1)若a∥b,∠1=50°,则∠2=
(2)若a∥b,∠1=50°,则∠3=
(3)若∠1=∠2, 则
(4)若∠1=∠4,则
50°
a∥b
130°
a∥b
两直线平行
同位角相等
内错角相等
同旁内角互补
两直线的位置关系
两角的数量关系
性质
两角的数量关系
两直线的位置关系
判定
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
例1 如图所示是一块梯形铁片的残余部分,量得∠A=100?,∠B=115°,梯形另外两个角各是多少度?
解:∵梯形上、下两底互相平行,
所以梯形的另外两个角分别是80°, 65°.
由图知 AB∥CD,
∴∠A+∠D=180°,
∠B+∠C=180°(两直线平行,同旁内角互补).
∴ ∠D=180°-∠A=180°-100°= 80°,
∠C=180°-∠B=180°-115°= 65°.
巩固新知,深化理解
1.如图,平行线AB,CD被直线AE所截, 已知∠1=110?,求∠2、 ∠3 、 ∠4的度数。
2. 如图,已知AB∥CD,AE∥CF,∠A=39°,
∠C是多少度?为什么?
巩固新知,深化理解
例2 如图,BCD是一条直线,∠A=75°,∠1=55°,∠2=75°,求∠B的度数.
解:∵ ∠A=∠2=75°(已知)
∴ AB∥CE (内错角相等,两直线平行)
∴ ∠B=∠1(两直线平行,同位角相等)
∵ ∠1=55°(已知)
∴ ∠B=55° (等量代换)
综合运用,熟练技能
解:∵AB//CD (已知)
∴∠C= ( )
又∵∠A=∠C(已知)
∴∠A= ( )
∴ // ( )
∴∠E=∠F ( )
A
D
E
C
B
F
两直线平行,同位角相等
等量代换
内错角相等,两直线平行
两直线平行,内错角相等
3. 完成下面的证明
如图,已知AB//CD,∠A=∠C,求证∠E=∠F .
综合运用,熟练技能
∠ABF
∠ABF
AE
FC
归纳小结
回顾本节课所学主要内容,你有什么收获?
能力拓展:如图,已知∠BAP与∠APD互补,∠1=∠2,求证:∠E=∠F
A
B
C
D
E
F
P
1
2
作业
必做题:课本习题5.3
第1、4、6、14 题
选做题:完成学案上能力拓展题
谢谢各位专家同仁莅临指导!
