内蒙古包头三十三中2012届高三上学期期末考试(数学文)
文档属性
| 名称 | 内蒙古包头三十三中2012届高三上学期期末考试(数学文) |

|
|
| 格式 | zip | ||
| 文件大小 | 212.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-01-14 00:00:00 | ||
图片预览




文档简介
包头三十三中高三年级期末考试试题
数学(文科)
第Ⅰ卷(选择题 共60分)
选择题(本大题共12小题,每小题5分,共计60分,把唯一正确的答案的代码填在答题卡上)
1.已知集合= ( )
A. B.
C. D.
2.已知向量,,,则k= ( )
A.1 B.2 C. 4 D. 8
3.设,则下列不等式中正确的是 ( )
A. B.
C. D.
4.方程在 ( )
A.没有根 B.有且仅有一个根
C.有且仅有两个根 D.有无穷多个根
5.若函数,则的定义域为 ( )
A. B.
C. D.
6.若变量x,y满足条件,则的最大值为 ( )
A.4 B.3 C.2 D.1
7.设偶函数满足,则 ( )
A. B.
C. D.
8.已知圆的方程为,设该圆过点的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为 ( )
A.10 B.20 C.30 D.40
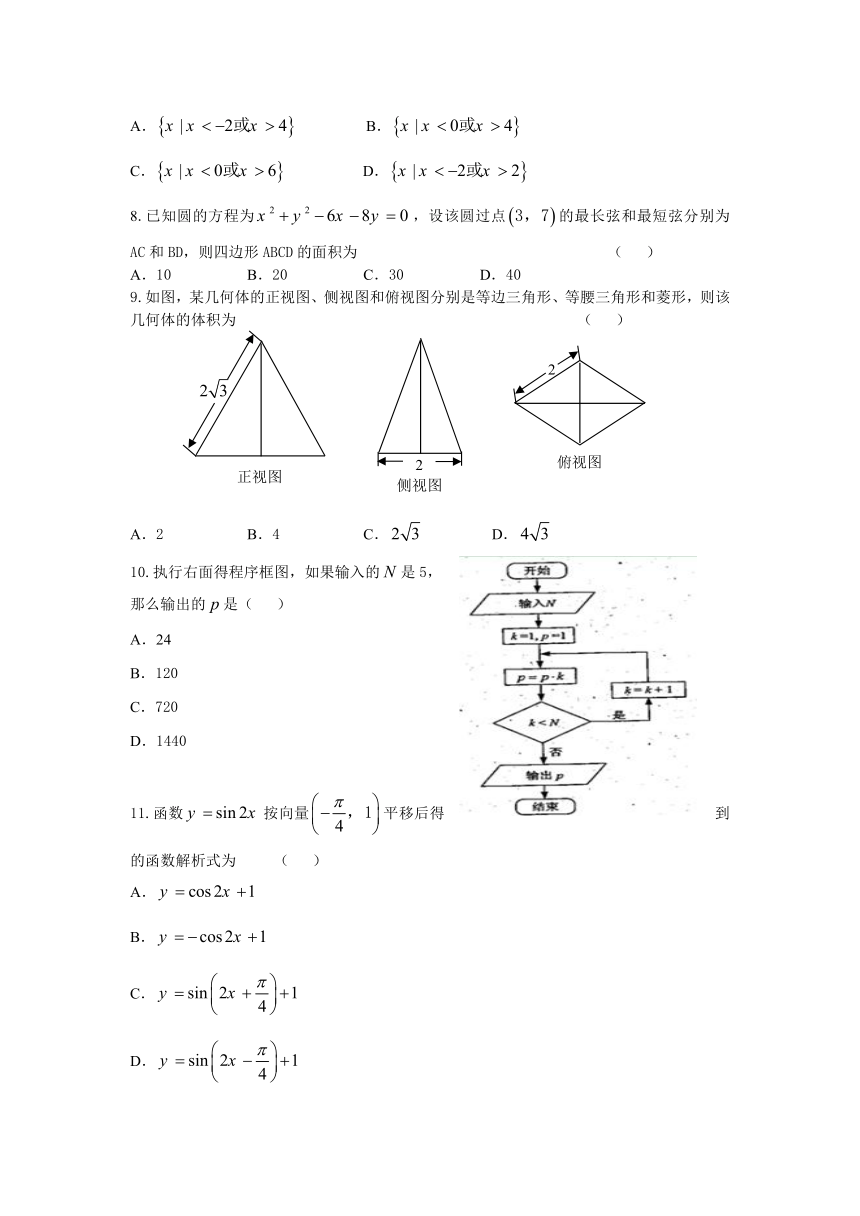
9.如图,某几何体的正视图、侧视图和俯视图分别是等边三角形、等腰三角形和菱形,则该几何体的体积为 ( )
A.2 B.4 C. D.
10.执行右面得程序框图,如果输入的是5,
那么输出的是( )
A.24
B.120
C.720
D.1440
11.函数按向量平移后得到的函数解析式为 ( )
A.
B.
C.
D.
12.设函数,则 ( )
A.在单调递增,其图像关于直线对称
B.在单调递增,其图像关于直线对称
C.在单调递减,其图像关于直线对称
D.在单调递减,其图像关于直线对称
包头三十三中高三年级数学(文科)期末试题
一、选择题答题卡(本大题共12小题,每小题5分,共计60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
选项
第Ⅱ卷 (非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,共计20分,将正确答案写在题中横线上)
13.抛物线的焦点坐标是 .
14.经过点,且在两坐标轴上的截距相等的直线方程是 .
15.设和为不重合的两个平面,给出下列命题:①若内的两条相交直线分别平行于内的两条直线,则∥;②若外的一条直线与内的一条直线平行,则∥;③设,若内有一条直线垂直于,则;④直线的充要条件是与内的两条直线垂直.其中所有的真命题的序号是 .
16.在中,为边上的一点,,,,若,则 .
三、解答题(本大题共6小题,共计70分,解答应写出必要的文字说明和解题步骤)
17.(本小题10分)已知函数.
(Ⅰ)求的最小正周期;
(Ⅱ)求在区间上的最大值和最小值.
18.(本小题12分)在等差数列中,,、、成等比数列,求数列的前n项和.
19.(本小题12分)如图,在四棱锥中,,,,∥,.
(Ⅰ)求证:;
(Ⅱ)求多面体的体积.
20.(本小题12分)设函数
(Ⅰ)求的值;
(Ⅱ)求的最小值.
21.(本小题12分)已知椭圆的中心在坐标原点,焦点在x轴上,且经过点,离心率为.
(Ⅰ)求椭圆P的方程;
(Ⅱ)是否存在过点的直线交椭圆于点、,且满足.若存在,求直线的方程;若不存在,说明理由.
22.(本小题12分) 已知函数.
(Ⅰ)当时,求曲线在点处的切线方程;
(Ⅱ)当时,讨论的单调性.
包头一中2011——2012学年度第一学期期末考试
高三年级文科数学试题答案
一、选择题(本大题共12小题,每小题5分,共计60分,把唯一正确的答案的代码填在答题卡上)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A D B C C B B D C B A B
二、填空题(本大题共4小题,每小题5分,共计20分,将正确答案写在题中横线上)
13. ;14. ;15. ①②;16.
三、解答题(本大题共6小题,共计70分,解答应写出必要的文字说明和解题步骤)
17.(本小题10分)
解:………………3分
(Ⅰ)………………………………5分
(Ⅱ)
…………………………6分
故当即时,取最大值;…………8分
当即时,取最小值0.………………10分
18.(本小题12分)
解:设等差数列的公差为d.
因为、、成等比数列,
所以.…………………………………2分
所以.
所以 ①…………………………4分
因为
所以 ②…………………………5分
由①②得:或……………………7分
若,则;……………………9分
若,则.…………12分
19.(本小题12分)
证明:(Ⅰ)
……………………2分
……………………4分
………………5分
……………………6分
(Ⅱ)解:连接AC
…………9分
∥,.
,
………………12分
20.(本小题12分)
解:(Ⅰ)……………………2分
………………4分
(Ⅱ)时,在上为减函数
…………………………7分
时,
…………8分
…………………………9分
即时,取得最小值.…………11分
因为,所以的最小值是.…………………………12分
21.(本小题12分)
解:(Ⅰ)设椭圆P的方程为.………………1分
由题意得:,……………………………………2分
……………………………………3分
故椭圆P的方程为……………………………………4分
(Ⅱ)假设存在满足题意的直线.易知当直线的斜率不存在时,不符合题意,故直线的斜率存在,设为k,则直线的方程为:.………………5分
由可得:………………6分
则,
设.则……………………7分
…………8分
……………………………………9分
……………………………………11分
直线的方程为:
故存在直线满足题意.…………………………12分
22.(本小题12分)
解:(Ⅰ) 当时,
所以 ,……………………1分
因此,.
即曲线1.…………2分
又 …………………………………………3分
所以曲线
……………………………………4分
(Ⅱ)因为,
所以 ,,…………5分
令
⑴当时,,,
所以,当x∈(0,1)时,,此时,函数单调递减
当时,,此时,,函数单调递增.……6分
⑵当时,由,即,解得, ……7分
① 当时,,恒成立,此时,函数在上单调递减;…………………………………………………………………………8分
② 当时,
时,,此时,函数单调递减
时,,此时,函数单调递增
时,,此时,函数单调递减…………10分
③ 当时,由于
时,,此时,函数单调递减;
时,,此时,函数单调递增.…………11分
综上所述:
当时,函数在上单调递减;函数在上单调递增
当时,函数在上单调递减
当时,函数在上单调递减;
函数 在上单调递增;
函数在上单调递减. ………………………………12分
版权所有:高考资源网(www.)
2
俯视图
侧视图
2
正视图
P
A
B
C
D
P
A
B
C
D
数学(文科)
第Ⅰ卷(选择题 共60分)
选择题(本大题共12小题,每小题5分,共计60分,把唯一正确的答案的代码填在答题卡上)
1.已知集合= ( )
A. B.
C. D.
2.已知向量,,,则k= ( )
A.1 B.2 C. 4 D. 8
3.设,则下列不等式中正确的是 ( )
A. B.
C. D.
4.方程在 ( )
A.没有根 B.有且仅有一个根
C.有且仅有两个根 D.有无穷多个根
5.若函数,则的定义域为 ( )
A. B.
C. D.
6.若变量x,y满足条件,则的最大值为 ( )
A.4 B.3 C.2 D.1
7.设偶函数满足,则 ( )
A. B.
C. D.
8.已知圆的方程为,设该圆过点的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为 ( )
A.10 B.20 C.30 D.40
9.如图,某几何体的正视图、侧视图和俯视图分别是等边三角形、等腰三角形和菱形,则该几何体的体积为 ( )
A.2 B.4 C. D.
10.执行右面得程序框图,如果输入的是5,
那么输出的是( )
A.24
B.120
C.720
D.1440
11.函数按向量平移后得到的函数解析式为 ( )
A.
B.
C.
D.
12.设函数,则 ( )
A.在单调递增,其图像关于直线对称
B.在单调递增,其图像关于直线对称
C.在单调递减,其图像关于直线对称
D.在单调递减,其图像关于直线对称
包头三十三中高三年级数学(文科)期末试题
一、选择题答题卡(本大题共12小题,每小题5分,共计60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
选项
第Ⅱ卷 (非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,共计20分,将正确答案写在题中横线上)
13.抛物线的焦点坐标是 .
14.经过点,且在两坐标轴上的截距相等的直线方程是 .
15.设和为不重合的两个平面,给出下列命题:①若内的两条相交直线分别平行于内的两条直线,则∥;②若外的一条直线与内的一条直线平行,则∥;③设,若内有一条直线垂直于,则;④直线的充要条件是与内的两条直线垂直.其中所有的真命题的序号是 .
16.在中,为边上的一点,,,,若,则 .
三、解答题(本大题共6小题,共计70分,解答应写出必要的文字说明和解题步骤)
17.(本小题10分)已知函数.
(Ⅰ)求的最小正周期;
(Ⅱ)求在区间上的最大值和最小值.
18.(本小题12分)在等差数列中,,、、成等比数列,求数列的前n项和.
19.(本小题12分)如图,在四棱锥中,,,,∥,.
(Ⅰ)求证:;
(Ⅱ)求多面体的体积.
20.(本小题12分)设函数
(Ⅰ)求的值;
(Ⅱ)求的最小值.
21.(本小题12分)已知椭圆的中心在坐标原点,焦点在x轴上,且经过点,离心率为.
(Ⅰ)求椭圆P的方程;
(Ⅱ)是否存在过点的直线交椭圆于点、,且满足.若存在,求直线的方程;若不存在,说明理由.
22.(本小题12分) 已知函数.
(Ⅰ)当时,求曲线在点处的切线方程;
(Ⅱ)当时,讨论的单调性.
包头一中2011——2012学年度第一学期期末考试
高三年级文科数学试题答案
一、选择题(本大题共12小题,每小题5分,共计60分,把唯一正确的答案的代码填在答题卡上)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A D B C C B B D C B A B
二、填空题(本大题共4小题,每小题5分,共计20分,将正确答案写在题中横线上)
13. ;14. ;15. ①②;16.
三、解答题(本大题共6小题,共计70分,解答应写出必要的文字说明和解题步骤)
17.(本小题10分)
解:………………3分
(Ⅰ)………………………………5分
(Ⅱ)
…………………………6分
故当即时,取最大值;…………8分
当即时,取最小值0.………………10分
18.(本小题12分)
解:设等差数列的公差为d.
因为、、成等比数列,
所以.…………………………………2分
所以.
所以 ①…………………………4分
因为
所以 ②…………………………5分
由①②得:或……………………7分
若,则;……………………9分
若,则.…………12分
19.(本小题12分)
证明:(Ⅰ)
……………………2分
……………………4分
………………5分
……………………6分
(Ⅱ)解:连接AC
…………9分
∥,.
,
………………12分
20.(本小题12分)
解:(Ⅰ)……………………2分
………………4分
(Ⅱ)时,在上为减函数
…………………………7分
时,
…………8分
…………………………9分
即时,取得最小值.…………11分
因为,所以的最小值是.…………………………12分
21.(本小题12分)
解:(Ⅰ)设椭圆P的方程为.………………1分
由题意得:,……………………………………2分
……………………………………3分
故椭圆P的方程为……………………………………4分
(Ⅱ)假设存在满足题意的直线.易知当直线的斜率不存在时,不符合题意,故直线的斜率存在,设为k,则直线的方程为:.………………5分
由可得:………………6分
则,
设.则……………………7分
…………8分
……………………………………9分
……………………………………11分
直线的方程为:
故存在直线满足题意.…………………………12分
22.(本小题12分)
解:(Ⅰ) 当时,
所以 ,……………………1分
因此,.
即曲线1.…………2分
又 …………………………………………3分
所以曲线
……………………………………4分
(Ⅱ)因为,
所以 ,,…………5分
令
⑴当时,,,
所以,当x∈(0,1)时,,此时,函数单调递减
当时,,此时,,函数单调递增.……6分
⑵当时,由,即,解得, ……7分
① 当时,,恒成立,此时,函数在上单调递减;…………………………………………………………………………8分
② 当时,
时,,此时,函数单调递减
时,,此时,函数单调递增
时,,此时,函数单调递减…………10分
③ 当时,由于
时,,此时,函数单调递减;
时,,此时,函数单调递增.…………11分
综上所述:
当时,函数在上单调递减;函数在上单调递增
当时,函数在上单调递减
当时,函数在上单调递减;
函数 在上单调递增;
函数在上单调递减. ………………………………12分
版权所有:高考资源网(www.)
2
俯视图
侧视图
2
正视图
P
A
B
C
D
P
A
B
C
D
同课章节目录
