人教版六年级数学下册《 正比例和反比例》同步测试题 (含解析)
文档属性
| 名称 | 人教版六年级数学下册《 正比例和反比例》同步测试题 (含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 203.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-14 13:52:23 | ||
图片预览



文档简介
人教版六年级数学下册《第4章
比例
第2课时
正比例和反比例》同步测试题
一.选择题(共6小题)
1.a与b成反比例关系的条件是( )
A.=c(一定)
B.a×c=b(一定)
C.a×b=c(一定)
2.一袋纯牛奶1.50元,购买纯牛奶的袋数和总钱数( )
A.成正比例
B.成反比例
C.不成比例
3.全班人数一定,出勤人数和出勤率( )
A.成正比例
B.成反比例
C.不成比例
4.表格中,若x和y成正比例,则k的值为( )
x
2
k
y
8
12
A.1.5
B.3
C.6
5.已知,当y一定时,x与z( )
A.成正比例关系
B.成反比例关系
C.不成比例关系
6.长方形的面积一定,长和宽( )
A.成正比例
B.成反比例
C.不成比例
二.填空题(共6小题)
7.小林骑自行车从家到学校,他骑车的速度和所需时间成
比例.
8.优优拿一些钱去买饮料,饮料的单价与购买的瓶数如表.
单价/元
1
2
4
5
6
瓶数
60
30
15
12
10
因为
一定,瓶数随着
的变化而变化.单价提高,瓶数
;单价降低,瓶数
,而且单价和瓶数的
一定,所以单价和瓶数成
比例关系.
9.如果y=5x,那么x和y成
比例.
10.=Y,XY成
比例;=Y,XY成
比例.
11.如图的统计图表示甲、乙两车同时从A地出发驶向B地的行驶时间和路程情况.请根据图回答以下问题:
(1)出发4分钟后,甲、乙两车相距
千米.
(2)甲车的速度是
千米/分.
(3)行驶6千米的路程,甲车比乙车少用
分钟.
(4)如图中表示甲车已经到达B地,那么乙车在速度不变的情况下从A地行驶到B地一共需要
分钟.
(5)如果甲车到达目的地后立即返回,则当乙车到达目的地时,甲、乙两车相距
千米.
12.小明只有10元钱,他买笔的枝数与笔的单价成反比例.
.
三.判断题(共5小题)
13.在同一幅地图上,图上距离越大实际距离就越大.
.(判断对错)
14.六二班的人数一定,每组的人数与组数成反比例.
.(判断对错)
15.分数值一定,它的分子和分母成正比例.
.(判断对错)
16.和一定,加数和另一个加数成正比例.
.(判断对错)
17.正比例与反比例的图象都是一条直线.
(判断对错)
四.应用题(共3小题)
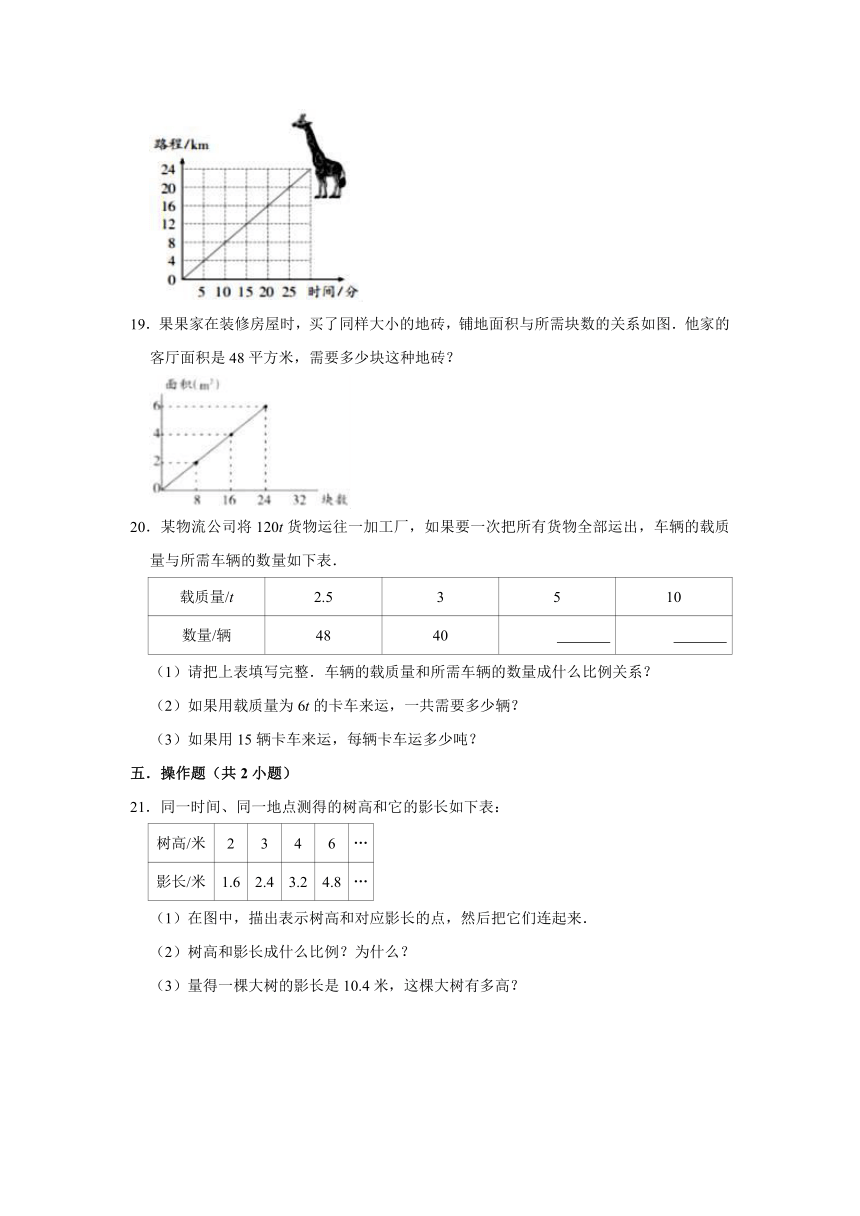
18.如图的图象表示长颈鹿的奔跑情况.
(1)长颈鹿的奔跑路程与奔跑时间成
比例关系.
(2)请你计算一下,长颈鹿16分钟跑多少千米?
19.果果家在装修房屋时,买了同样大小的地砖,铺地面积与所需块数的关系如图.他家的客厅面积是48平方米,需要多少块这种地砖?
20.某物流公司将120t货物运往一加工厂,如果要一次把所有货物全部运出,车辆的载质量与所需车辆的数量如下表.
载质量/t
2.5
3
5
10
数量/辆
48
40
(1)请把上表填写完整.车辆的载质量和所需车辆的数量成什么比例关系?
(2)如果用载质量为6t的卡车来运,一共需要多少辆?
(3)如果用15辆卡车来运,每辆卡车运多少吨?
五.操作题(共2小题)
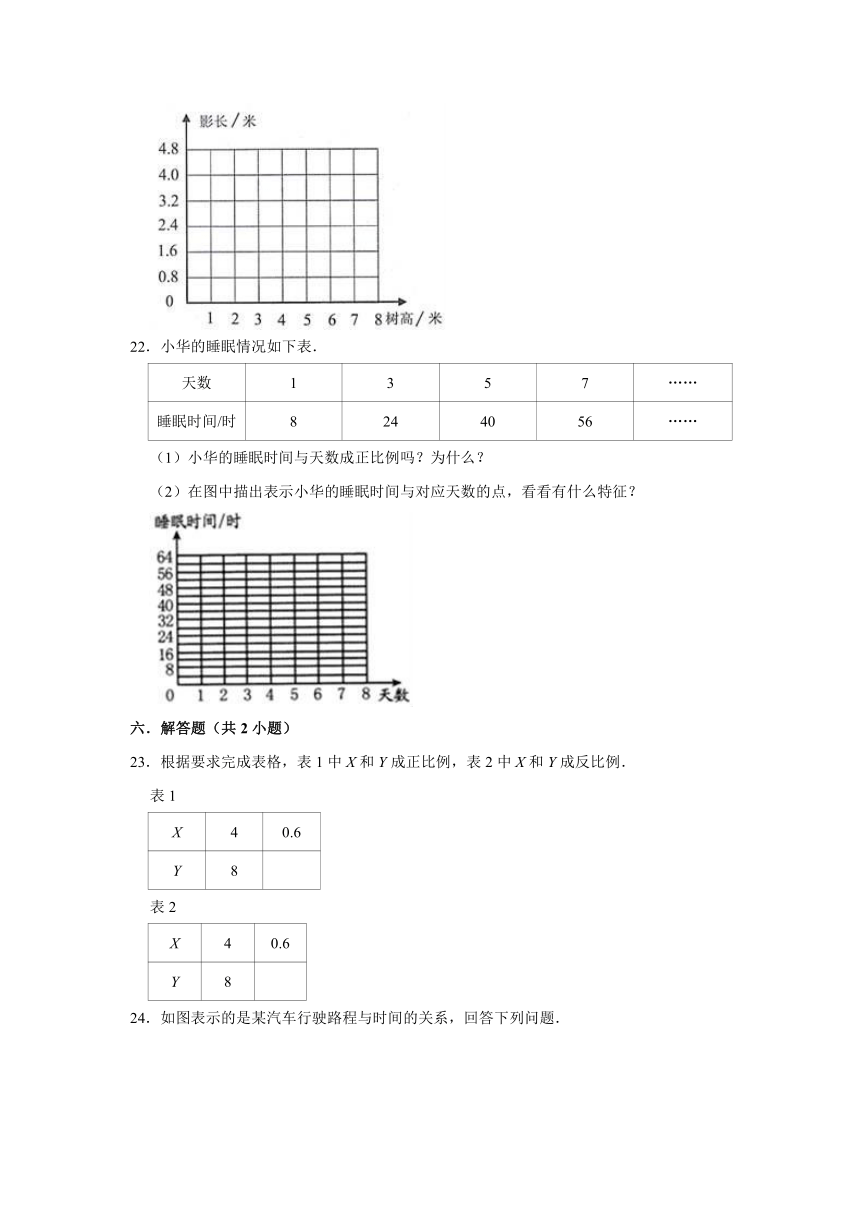
21.同一时间、同一地点测得的树高和它的影长如下表:
树高/米
2
3
4
6
…
影长/米
1.6
2.4
3.2
4.8
…
(1)在图中,描出表示树高和对应影长的点,然后把它们连起来.
(2)树高和影长成什么比例?为什么?
(3)量得一棵大树的影长是10.4米,这棵大树有多高?
22.小华的睡眠情况如下表.
天数
1
3
5
7
……
睡眠时间/时
8
24
40
56
……
(1)小华的睡眠时间与天数成正比例吗?为什么?
(2)在图中描出表示小华的睡眠时间与对应天数的点,看看有什么特征?
六.解答题(共2小题)
23.根据要求完成表格,表1中X和Y成正比例,表2中X和Y成反比例.
表1
X
4
0.6
Y
8
表2
X
4
0.6
Y
8
24.如图表示的是某汽车行驶路程与时间的关系,回答下列问题.
(1)图上的点A表示该汽车已经行驶了多长时间?行驶了多少千米?
(2)该汽车的速度是多少?
(3)看图分析(不计算)该汽车行驶30km需要多长时间,把你的想法写一写.
参考答案与试题解析
一.选择题(共6小题)
1.【分析】根据反比例的意义分析后直接选择即可.
【解答】解:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.只有a×b=c(一定),a与b才成反比例.只有C选项符合反比例的意义.
故选:C.
【点评】此题重点考查反比例的意义,两个变量的乘积一定.
2.【分析】判断购买纯牛奶的袋数和总钱数成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例.
【解答】解:购买电纯牛奶的钱数÷总袋数=每袋纯牛奶的价格(一定),是比值一定,购买纯牛奶袋数和总钱数成正比例.
故选:A.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断.
3.【分析】判断出勤人数和出勤率成不成什么比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例,如果是其它的量一定,就不成比例.
【解答】解;出勤人数=出勤率×全班人数(一定),是比值一定,故出勤人数和出勤率成比例.
故选:A。
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它的量一定,再做选择.
4.【分析】因为x和y成正比例,则x与y的商一定,从而可以得一个比例式,进而求得K的值。
【解答】解:由题意可得:
k=3;
故选:B。
【点评】解答此题的关键是:利用成正比例的量的商一定,得到比例式,求解即可。
5.【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:已知,所以=y(一定),当y一定时,x与z成正比例.
故选:A.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
6.【分析】根据正比例的意义x:y=k(一定)和反比例的意义xy=k(一定),因为长×宽=长方形的面积(一定),符合反比例的意义.
【解答】解:根据长方形的面积公式,长×宽=长方形的面积(一定),符合反比例的意义xy=k(一定),所以长方形的面积一定,长和宽成反比例.
故选:B。
【点评】此题主要考查正、反比例的意义,以及长方形的面积公式.
二.填空题(共6小题)
7.【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系;根据时间、速度、路程之间的关系进行分析.
【解答】解:速度×时间=路程
小林骑车的速度和所需时间是两种相关联的量,时间随速度的变化而变化,小林从家到学校的路程不变,也就是速度与时间的乘积是一定的.所以小林骑车的速度和所需时间是成反比例关系.
故答案为:反.
【点评】此题重点考查辨识成正比例的量与成反比例的量和时间、速度、路程之间的关系.
8.【分析】通过观察表中数量,发现单价和瓶数是相关联的量,单价变化,瓶数也随着变化,通过计算出单价与数量的乘积,发现单价和瓶数的积一定,符合反比例的意义,所以单价和瓶数是反比例的关系.
【解答】解:1×60=60
2×30=60
3×20=60
4×15=60
5×12=60
可得:因为总价一定,瓶数随着单价的变化而变化,单价提高,瓶数减少;单价降低,瓶数增加,而且单价和瓶数的积一定,我所以单价和瓶数成反比例关系.
故答案为:总价,单价,减少,增加,积,反.
【点评】此题主要考查正、反比例的意义,知识点:成反比例关系的两种量必须具备:①相关联;②一种量变化,另一种量也随着变化,且变化方向相反;③这两种量中相对应的两个量的积一定.
9.【分析】判断x和y成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例.
【解答】解:因为y=5x,所以y:x=5(一定),是比值一定,x和y成正比例.
故答案为:正.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断.
10.【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,据此解答.
【解答】解:因为,=Y,则X:Y=5(一定);
所以,XY成正比例;
因为,=Y,则XY=5(一定);
所以,XY成反比例.
故答案为:正,反.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断.
11.【分析】(1)从图中可以看出,甲车4分钟行驶4千米,乙车4分钟行驶2千米,甲、乙两车相距4﹣2=2千米;
(2)从图中可以看出,甲车的速度是1千米/分;
(3)从图中可以看出,甲车行驶6千米,用6分钟;乙车行驶6千米,用12分钟,求甲车比乙车少用多少分钟,用12减去6即可解答;
(4)根据乙车4分钟行驶2千米,求出乙车的速度是多少,再根据时间=路程÷速度即可解答;
(5)分别求出甲乙两车行驶的时间,乙车比甲车多用的时间,就是甲车返回的路程,也就是甲乙两车的距离.
【解答】解:(1)甲车4分钟行驶4千米,乙车4分钟行驶2千米,
4﹣2=2(千米);
答:出发4分钟后,甲、乙两车相距2千米.
(2)从图中可以看出,甲车的速度是1千米/分;
(3)从图中可以看出,甲车行驶6千米,用6分钟;乙车行驶6千米,用12分钟,
12﹣6=6(分钟);
答:甲车比乙车少用6分钟.
(4)根据乙车4分钟行驶2千米,
8÷(2÷4)
=8÷0.5
=16(分钟);
答:乙车在速度不变的情况下从A地行驶到B地一共需要16分钟.
(5)8÷8=1(小时)
12÷6=2(小时)
2﹣1=1(小时)
8×1=8(千米)
答:甲、乙两车相距8千米.
故答案为:2;1;6;16;8.
【点评】认真审题,从统计图中获取信息,掌握路程、速度和时间三者的关系是解题的关键.
12.【分析】判断买笔的枝数与笔的单价是不是成反比例,就看这两种量是不是对应数的乘积一定,如果乘积一定,就成反比例.
【解答】解:笔的枝数×笔的单价=10元钱(一定),是乘积一定,
所以买笔的枝数与笔的单价就成反比例.
故答案为:正确.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应数的比值一定,还是对应数的乘积一定,再做出判断.
三.判断题(共5小题)
13.【分析】对的,因为比例尺相同,实际距离与图上距离成正比.
【解答】解:因为图上距离:实际距离=比例尺一定,
所以在同一幅地图上,图上距离与实际距离成正比例,
故在同一幅地图上,图上距离越大实际距离就越大.
故答案为:√.
【点评】本题结合比例尺考查了正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.
14.【分析】判断每组的人数与组数是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果是乘积不一定,就不成反比例.
【解答】解:每组的人数×组数=六二班的总人数(一定),是乘积一定,每组的人数与组数就成反比例.
故判断为:正确.
【点评】此题属于辨识成反比例的量,就看这两种量是否是对应的乘积一定,再做出判断.
15.【分析】分子除以分母等于分数值,分数值一定,是比值一定,分子和分母成正比例,由此做出判断.
【解答】解:=分数值(一定),是比值一定,分子和分母成正比例.
故判断为:正确.
【点评】判断两种量是否成正反比例,要看这两种量是对应的比值一定,还是乘积一定,再做出判断.
16.【分析】判定两种量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定,就成反比例.
【解答】解:因为:加数+加数=和(一定),是两个数的和一定,不是商一定,也不是积一定,所以一个加数和另一个加数不成比例;
故答案为:×.
【点评】此题属于根据正、反比例的意义,判断两种相关联的成正比例还是成反比例,就看是对应的比值一定,还是对应的乘积一定,再做出解答.
17.【分析】根据正、反比例的意义,正比例是相对应的两个数的比值一定,反比例是相对应的两个数的乘积一定.
【解答】解:正比例的图象的一条直线,而反比例的图象是一条曲线.
因此,正比例与反比例的图象都是一条直线.这种说法是错误的.
故答案为:×.
【点评】此题考查的目的是理解掌握正、反比例的意义及应用.
四.应用题(共3小题)
18.【分析】(1)通过观察图可知,=速度(一定),所以长颈鹿的奔跑路程与奔跑时间成正比例关系.
(2)设16分钟跑x千米,据此列比例解答.
【解答】解:(1)因为=速度(一定),所以长颈鹿的奔跑路程与奔跑时间成正比例关系.
(2)设16分钟跑x千米,
=
5x=4×16
x=
x=12.8
答:长颈鹿16分钟跑12.8千米.
故答案为:正.
【点评】此题考查的目的是理解掌握正比例的意义及应用,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(即两个数的商)一定,这两种就叫做成正比例的量,它们的关系就是正比例关系.
19.【分析】通过观察图象可知,因为正比例图象是一条直线,所以需要地砖的块数和铺地的面积成正比例,设需要x块这种地砖,据此列比例解答.
【解答】解:设需要x块这种地砖,
=
2x=8×48
x=
x=192
答:需要这种地砖192块.
【点评】此题考查的目的是理解掌握正比例的意义及应用.两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(即两个数的商)一定,这两种就叫做成正比例的量,它们的关系就是正比例关系.
20.【分析】2.5×48=3×40=120,得出:运用车辆的载重量×所需车辆的数量=总重量,则用总重量分别除以5,10求出各用的辆数.填写统计表.
(1)由统计表中的数量可以看出,车辆的载重量与所需车辆的数量的乘积一定,所以车辆的载重量与所需车辆的数量成反比例.
(2)运用总重量除以6就是运用卡车的量数.
(3)运用总重量除以卡车的量数15就是每辆卡车运多少吨.
【解答】解:3×40÷5
=120÷5
=24(辆)
3×40÷10
=120÷10
=12(辆)
载质量/t
2.5
3
5
10
数量/辆
48
40
24
12
(1)因为2.5×48=120(吨)
3×40=120(吨)
因为车辆的载重量与所需车辆的数量的乘积一定,
所以车辆的载重量与所需车辆的数量成反比例.
(2)120÷5=24(辆)
答:用载重量6吨的卡车来运,一共需要24辆.
(3)120÷15=8(吨)
答:每辆卡车运8吨.
故答案为:24;12.
【点评】本题考查了学生正反比例的判断情况,能运用统计表提供的信息解决问题.同时考查了学生理解分析问题的能力.
五.操作题(共2小题)
21.【分析】(1)在图中找出(树高,影长)表示的点,描出表示树高和对应影长的图象即可.
(2)首先求出树高和影长的比各是多少,即可判断出树高和影长成比例,然后根据正、反比例的特征,可得树高和影长成正比例,原因是树高和影长的比值一定,据此解答即可.
(3)根据题意,用这棵树的影长乘以树高和影长的比值,求出这棵树的高度为多少米即可.
【解答】解:(1)
(2)因为2:1.6=1.25
3:2.4=1.25
4:3.2=1.25
6:4.8=1.25
因为树高和影长的比值一定,
所以树高和影长成比例,而且成正比例.
(3)10.4×1.25=13(米)
答:这棵树的高度为13米.
【点评】此题主要考查了正、反比例应用题,要熟练掌握,解答此题的关键是要明确正比例、反比例的特征:(1)成正比例关系的这两种量中相对应的两个数的比值(即商)一定.(2)成反比例关系的这两种量中相对应的两个数的积一定.
22.【分析】(1)判断两个相关联的量之间是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例.
(2)根据统计表绘制统计图,然后观察如图,得出特征.
【解答】解:(1)8:1=24:340:5=56:7=8(一定)
答:小华睡眠所用的时间与天数成正比,因为小华的睡眠所用的时间与天数的比值一定.
(2)如图所示;
观察图形发现正比例的图象是一条射线.
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断.
六.解答题(共2小题)
23.【分析】(1)表1中的两个数成正比例,也就是X和Y的比值不变,由此可以得出比例4:8=0.6:Y,再根据比例的基本性质进行解答即可;
(2)表2中的两个数成反比例,也就是X和Y的积不变,由此可以得出0.6Y=4×8,再根据等式的性质进行解答即可.
【解答】解:(1)表1中的两个数成正比例可得:
4:8=0.6:Y
4Y=8×0.6
4Y÷4=8×0.6÷4
y=1.2
X
4
0.6
Y
8
1.2
(2)表2中的两个数成反比例可得:
0.6Y=4×8
0.6Y÷0.6=4×8÷0.6
Y=
X
4
0.6
Y
8
故答案为:1.2,.
【点评】本题主要考查学生对于正.反比例知识的掌握情况.
24.【分析】(1)图中直观显示,点A行驶的时间是3小时,行驶路程是180km.
(2)根据速度=路程÷时间可求得.
(3)先从纵轴上找到30km
的点,过这个点作纵轴的垂线,交图象于一点,再过这个点向横轴作垂线,垂足对应的点所表示的时间就是所求的时间.
【解答】解;(1)由图示可知:点A表示该汽车已经行驶了3小时,行驶了180千米.
(2)180÷3=60(km/h)
答:汽车的速度是60km/h.
(3)
先从纵轴上找到30km
的点,过这个点作纵轴的垂线,交图象于一点,再过这个点向横轴作垂线,垂足对应的点所表示的时间0.5小时就是汽车行驶30km需要的时间.
【点评】此题考查了正比例关系的图象的应用,利用数形结合的思想解决问题是常用的一种数学思想方法.
比例
第2课时
正比例和反比例》同步测试题
一.选择题(共6小题)
1.a与b成反比例关系的条件是( )
A.=c(一定)
B.a×c=b(一定)
C.a×b=c(一定)
2.一袋纯牛奶1.50元,购买纯牛奶的袋数和总钱数( )
A.成正比例
B.成反比例
C.不成比例
3.全班人数一定,出勤人数和出勤率( )
A.成正比例
B.成反比例
C.不成比例
4.表格中,若x和y成正比例,则k的值为( )
x
2
k
y
8
12
A.1.5
B.3
C.6
5.已知,当y一定时,x与z( )
A.成正比例关系
B.成反比例关系
C.不成比例关系
6.长方形的面积一定,长和宽( )
A.成正比例
B.成反比例
C.不成比例
二.填空题(共6小题)
7.小林骑自行车从家到学校,他骑车的速度和所需时间成
比例.
8.优优拿一些钱去买饮料,饮料的单价与购买的瓶数如表.
单价/元
1
2
4
5
6
瓶数
60
30
15
12
10
因为
一定,瓶数随着
的变化而变化.单价提高,瓶数
;单价降低,瓶数
,而且单价和瓶数的
一定,所以单价和瓶数成
比例关系.
9.如果y=5x,那么x和y成
比例.
10.=Y,XY成
比例;=Y,XY成
比例.
11.如图的统计图表示甲、乙两车同时从A地出发驶向B地的行驶时间和路程情况.请根据图回答以下问题:
(1)出发4分钟后,甲、乙两车相距
千米.
(2)甲车的速度是
千米/分.
(3)行驶6千米的路程,甲车比乙车少用
分钟.
(4)如图中表示甲车已经到达B地,那么乙车在速度不变的情况下从A地行驶到B地一共需要
分钟.
(5)如果甲车到达目的地后立即返回,则当乙车到达目的地时,甲、乙两车相距
千米.
12.小明只有10元钱,他买笔的枝数与笔的单价成反比例.
.
三.判断题(共5小题)
13.在同一幅地图上,图上距离越大实际距离就越大.
.(判断对错)
14.六二班的人数一定,每组的人数与组数成反比例.
.(判断对错)
15.分数值一定,它的分子和分母成正比例.
.(判断对错)
16.和一定,加数和另一个加数成正比例.
.(判断对错)
17.正比例与反比例的图象都是一条直线.
(判断对错)
四.应用题(共3小题)
18.如图的图象表示长颈鹿的奔跑情况.
(1)长颈鹿的奔跑路程与奔跑时间成
比例关系.
(2)请你计算一下,长颈鹿16分钟跑多少千米?
19.果果家在装修房屋时,买了同样大小的地砖,铺地面积与所需块数的关系如图.他家的客厅面积是48平方米,需要多少块这种地砖?
20.某物流公司将120t货物运往一加工厂,如果要一次把所有货物全部运出,车辆的载质量与所需车辆的数量如下表.
载质量/t
2.5
3
5
10
数量/辆
48
40
(1)请把上表填写完整.车辆的载质量和所需车辆的数量成什么比例关系?
(2)如果用载质量为6t的卡车来运,一共需要多少辆?
(3)如果用15辆卡车来运,每辆卡车运多少吨?
五.操作题(共2小题)
21.同一时间、同一地点测得的树高和它的影长如下表:
树高/米
2
3
4
6
…
影长/米
1.6
2.4
3.2
4.8
…
(1)在图中,描出表示树高和对应影长的点,然后把它们连起来.
(2)树高和影长成什么比例?为什么?
(3)量得一棵大树的影长是10.4米,这棵大树有多高?
22.小华的睡眠情况如下表.
天数
1
3
5
7
……
睡眠时间/时
8
24
40
56
……
(1)小华的睡眠时间与天数成正比例吗?为什么?
(2)在图中描出表示小华的睡眠时间与对应天数的点,看看有什么特征?
六.解答题(共2小题)
23.根据要求完成表格,表1中X和Y成正比例,表2中X和Y成反比例.
表1
X
4
0.6
Y
8
表2
X
4
0.6
Y
8
24.如图表示的是某汽车行驶路程与时间的关系,回答下列问题.
(1)图上的点A表示该汽车已经行驶了多长时间?行驶了多少千米?
(2)该汽车的速度是多少?
(3)看图分析(不计算)该汽车行驶30km需要多长时间,把你的想法写一写.
参考答案与试题解析
一.选择题(共6小题)
1.【分析】根据反比例的意义分析后直接选择即可.
【解答】解:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.只有a×b=c(一定),a与b才成反比例.只有C选项符合反比例的意义.
故选:C.
【点评】此题重点考查反比例的意义,两个变量的乘积一定.
2.【分析】判断购买纯牛奶的袋数和总钱数成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例.
【解答】解:购买电纯牛奶的钱数÷总袋数=每袋纯牛奶的价格(一定),是比值一定,购买纯牛奶袋数和总钱数成正比例.
故选:A.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断.
3.【分析】判断出勤人数和出勤率成不成什么比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例,如果是其它的量一定,就不成比例.
【解答】解;出勤人数=出勤率×全班人数(一定),是比值一定,故出勤人数和出勤率成比例.
故选:A。
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它的量一定,再做选择.
4.【分析】因为x和y成正比例,则x与y的商一定,从而可以得一个比例式,进而求得K的值。
【解答】解:由题意可得:
k=3;
故选:B。
【点评】解答此题的关键是:利用成正比例的量的商一定,得到比例式,求解即可。
5.【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:已知,所以=y(一定),当y一定时,x与z成正比例.
故选:A.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
6.【分析】根据正比例的意义x:y=k(一定)和反比例的意义xy=k(一定),因为长×宽=长方形的面积(一定),符合反比例的意义.
【解答】解:根据长方形的面积公式,长×宽=长方形的面积(一定),符合反比例的意义xy=k(一定),所以长方形的面积一定,长和宽成反比例.
故选:B。
【点评】此题主要考查正、反比例的意义,以及长方形的面积公式.
二.填空题(共6小题)
7.【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系;根据时间、速度、路程之间的关系进行分析.
【解答】解:速度×时间=路程
小林骑车的速度和所需时间是两种相关联的量,时间随速度的变化而变化,小林从家到学校的路程不变,也就是速度与时间的乘积是一定的.所以小林骑车的速度和所需时间是成反比例关系.
故答案为:反.
【点评】此题重点考查辨识成正比例的量与成反比例的量和时间、速度、路程之间的关系.
8.【分析】通过观察表中数量,发现单价和瓶数是相关联的量,单价变化,瓶数也随着变化,通过计算出单价与数量的乘积,发现单价和瓶数的积一定,符合反比例的意义,所以单价和瓶数是反比例的关系.
【解答】解:1×60=60
2×30=60
3×20=60
4×15=60
5×12=60
可得:因为总价一定,瓶数随着单价的变化而变化,单价提高,瓶数减少;单价降低,瓶数增加,而且单价和瓶数的积一定,我所以单价和瓶数成反比例关系.
故答案为:总价,单价,减少,增加,积,反.
【点评】此题主要考查正、反比例的意义,知识点:成反比例关系的两种量必须具备:①相关联;②一种量变化,另一种量也随着变化,且变化方向相反;③这两种量中相对应的两个量的积一定.
9.【分析】判断x和y成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例.
【解答】解:因为y=5x,所以y:x=5(一定),是比值一定,x和y成正比例.
故答案为:正.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断.
10.【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,据此解答.
【解答】解:因为,=Y,则X:Y=5(一定);
所以,XY成正比例;
因为,=Y,则XY=5(一定);
所以,XY成反比例.
故答案为:正,反.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断.
11.【分析】(1)从图中可以看出,甲车4分钟行驶4千米,乙车4分钟行驶2千米,甲、乙两车相距4﹣2=2千米;
(2)从图中可以看出,甲车的速度是1千米/分;
(3)从图中可以看出,甲车行驶6千米,用6分钟;乙车行驶6千米,用12分钟,求甲车比乙车少用多少分钟,用12减去6即可解答;
(4)根据乙车4分钟行驶2千米,求出乙车的速度是多少,再根据时间=路程÷速度即可解答;
(5)分别求出甲乙两车行驶的时间,乙车比甲车多用的时间,就是甲车返回的路程,也就是甲乙两车的距离.
【解答】解:(1)甲车4分钟行驶4千米,乙车4分钟行驶2千米,
4﹣2=2(千米);
答:出发4分钟后,甲、乙两车相距2千米.
(2)从图中可以看出,甲车的速度是1千米/分;
(3)从图中可以看出,甲车行驶6千米,用6分钟;乙车行驶6千米,用12分钟,
12﹣6=6(分钟);
答:甲车比乙车少用6分钟.
(4)根据乙车4分钟行驶2千米,
8÷(2÷4)
=8÷0.5
=16(分钟);
答:乙车在速度不变的情况下从A地行驶到B地一共需要16分钟.
(5)8÷8=1(小时)
12÷6=2(小时)
2﹣1=1(小时)
8×1=8(千米)
答:甲、乙两车相距8千米.
故答案为:2;1;6;16;8.
【点评】认真审题,从统计图中获取信息,掌握路程、速度和时间三者的关系是解题的关键.
12.【分析】判断买笔的枝数与笔的单价是不是成反比例,就看这两种量是不是对应数的乘积一定,如果乘积一定,就成反比例.
【解答】解:笔的枝数×笔的单价=10元钱(一定),是乘积一定,
所以买笔的枝数与笔的单价就成反比例.
故答案为:正确.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应数的比值一定,还是对应数的乘积一定,再做出判断.
三.判断题(共5小题)
13.【分析】对的,因为比例尺相同,实际距离与图上距离成正比.
【解答】解:因为图上距离:实际距离=比例尺一定,
所以在同一幅地图上,图上距离与实际距离成正比例,
故在同一幅地图上,图上距离越大实际距离就越大.
故答案为:√.
【点评】本题结合比例尺考查了正比例:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.
14.【分析】判断每组的人数与组数是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果是乘积不一定,就不成反比例.
【解答】解:每组的人数×组数=六二班的总人数(一定),是乘积一定,每组的人数与组数就成反比例.
故判断为:正确.
【点评】此题属于辨识成反比例的量,就看这两种量是否是对应的乘积一定,再做出判断.
15.【分析】分子除以分母等于分数值,分数值一定,是比值一定,分子和分母成正比例,由此做出判断.
【解答】解:=分数值(一定),是比值一定,分子和分母成正比例.
故判断为:正确.
【点评】判断两种量是否成正反比例,要看这两种量是对应的比值一定,还是乘积一定,再做出判断.
16.【分析】判定两种量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定,就成反比例.
【解答】解:因为:加数+加数=和(一定),是两个数的和一定,不是商一定,也不是积一定,所以一个加数和另一个加数不成比例;
故答案为:×.
【点评】此题属于根据正、反比例的意义,判断两种相关联的成正比例还是成反比例,就看是对应的比值一定,还是对应的乘积一定,再做出解答.
17.【分析】根据正、反比例的意义,正比例是相对应的两个数的比值一定,反比例是相对应的两个数的乘积一定.
【解答】解:正比例的图象的一条直线,而反比例的图象是一条曲线.
因此,正比例与反比例的图象都是一条直线.这种说法是错误的.
故答案为:×.
【点评】此题考查的目的是理解掌握正、反比例的意义及应用.
四.应用题(共3小题)
18.【分析】(1)通过观察图可知,=速度(一定),所以长颈鹿的奔跑路程与奔跑时间成正比例关系.
(2)设16分钟跑x千米,据此列比例解答.
【解答】解:(1)因为=速度(一定),所以长颈鹿的奔跑路程与奔跑时间成正比例关系.
(2)设16分钟跑x千米,
=
5x=4×16
x=
x=12.8
答:长颈鹿16分钟跑12.8千米.
故答案为:正.
【点评】此题考查的目的是理解掌握正比例的意义及应用,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(即两个数的商)一定,这两种就叫做成正比例的量,它们的关系就是正比例关系.
19.【分析】通过观察图象可知,因为正比例图象是一条直线,所以需要地砖的块数和铺地的面积成正比例,设需要x块这种地砖,据此列比例解答.
【解答】解:设需要x块这种地砖,
=
2x=8×48
x=
x=192
答:需要这种地砖192块.
【点评】此题考查的目的是理解掌握正比例的意义及应用.两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(即两个数的商)一定,这两种就叫做成正比例的量,它们的关系就是正比例关系.
20.【分析】2.5×48=3×40=120,得出:运用车辆的载重量×所需车辆的数量=总重量,则用总重量分别除以5,10求出各用的辆数.填写统计表.
(1)由统计表中的数量可以看出,车辆的载重量与所需车辆的数量的乘积一定,所以车辆的载重量与所需车辆的数量成反比例.
(2)运用总重量除以6就是运用卡车的量数.
(3)运用总重量除以卡车的量数15就是每辆卡车运多少吨.
【解答】解:3×40÷5
=120÷5
=24(辆)
3×40÷10
=120÷10
=12(辆)
载质量/t
2.5
3
5
10
数量/辆
48
40
24
12
(1)因为2.5×48=120(吨)
3×40=120(吨)
因为车辆的载重量与所需车辆的数量的乘积一定,
所以车辆的载重量与所需车辆的数量成反比例.
(2)120÷5=24(辆)
答:用载重量6吨的卡车来运,一共需要24辆.
(3)120÷15=8(吨)
答:每辆卡车运8吨.
故答案为:24;12.
【点评】本题考查了学生正反比例的判断情况,能运用统计表提供的信息解决问题.同时考查了学生理解分析问题的能力.
五.操作题(共2小题)
21.【分析】(1)在图中找出(树高,影长)表示的点,描出表示树高和对应影长的图象即可.
(2)首先求出树高和影长的比各是多少,即可判断出树高和影长成比例,然后根据正、反比例的特征,可得树高和影长成正比例,原因是树高和影长的比值一定,据此解答即可.
(3)根据题意,用这棵树的影长乘以树高和影长的比值,求出这棵树的高度为多少米即可.
【解答】解:(1)
(2)因为2:1.6=1.25
3:2.4=1.25
4:3.2=1.25
6:4.8=1.25
因为树高和影长的比值一定,
所以树高和影长成比例,而且成正比例.
(3)10.4×1.25=13(米)
答:这棵树的高度为13米.
【点评】此题主要考查了正、反比例应用题,要熟练掌握,解答此题的关键是要明确正比例、反比例的特征:(1)成正比例关系的这两种量中相对应的两个数的比值(即商)一定.(2)成反比例关系的这两种量中相对应的两个数的积一定.
22.【分析】(1)判断两个相关联的量之间是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例.
(2)根据统计表绘制统计图,然后观察如图,得出特征.
【解答】解:(1)8:1=24:340:5=56:7=8(一定)
答:小华睡眠所用的时间与天数成正比,因为小华的睡眠所用的时间与天数的比值一定.
(2)如图所示;
观察图形发现正比例的图象是一条射线.
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断.
六.解答题(共2小题)
23.【分析】(1)表1中的两个数成正比例,也就是X和Y的比值不变,由此可以得出比例4:8=0.6:Y,再根据比例的基本性质进行解答即可;
(2)表2中的两个数成反比例,也就是X和Y的积不变,由此可以得出0.6Y=4×8,再根据等式的性质进行解答即可.
【解答】解:(1)表1中的两个数成正比例可得:
4:8=0.6:Y
4Y=8×0.6
4Y÷4=8×0.6÷4
y=1.2
X
4
0.6
Y
8
1.2
(2)表2中的两个数成反比例可得:
0.6Y=4×8
0.6Y÷0.6=4×8÷0.6
Y=
X
4
0.6
Y
8
故答案为:1.2,.
【点评】本题主要考查学生对于正.反比例知识的掌握情况.
24.【分析】(1)图中直观显示,点A行驶的时间是3小时,行驶路程是180km.
(2)根据速度=路程÷时间可求得.
(3)先从纵轴上找到30km
的点,过这个点作纵轴的垂线,交图象于一点,再过这个点向横轴作垂线,垂足对应的点所表示的时间就是所求的时间.
【解答】解;(1)由图示可知:点A表示该汽车已经行驶了3小时,行驶了180千米.
(2)180÷3=60(km/h)
答:汽车的速度是60km/h.
(3)
先从纵轴上找到30km
的点,过这个点作纵轴的垂线,交图象于一点,再过这个点向横轴作垂线,垂足对应的点所表示的时间0.5小时就是汽车行驶30km需要的时间.
【点评】此题考查了正比例关系的图象的应用,利用数形结合的思想解决问题是常用的一种数学思想方法.
