人教版六年级数学下册《 正比例和反比例》同步测试题(含解析)
文档属性
| 名称 | 人教版六年级数学下册《 正比例和反比例》同步测试题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 222.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-14 14:08:31 | ||
图片预览



文档简介
人教版六年级数学下册《第4章
比例
第2课时
正比例和反比例》同步测试题
一.选择题(共6小题)
1.下列等式中,a与b(a、b均不为0)成反比例的是( )
A.2a=5b
B.a×7=
C.a×=1
2.下列两种量的关系成正比例关系的是( )
A.圆的半径和圆的面积
B.写字总数一定,写一个字所用时间和写字总时间
C.写字总数一定,每分钟写字个数和写字总时间
D.两个互相咬合的齿轮,齿轮的齿数和转数
3.圆的周长和直径( )
A.成正比例
B.成反比例
C.不成比例
4.a和b成反比例关系的式子是( )
A.5a=4b
B.=
C.5a=
D.5a=b+4
5.如果ab=3,那么a与b( )
A.不成比例
B.成反比例
C.成正比例
6.总价一定,单价和数量( )
A.成正比例
B.成反比例
C.不成比例
D.以上都不对
二.填空题(共6小题)
7.A、B、C三量的关系时A×B=C中,当C一定时,A和B成
关系.
8.表格中,如果A和B成正比例,x=
,如果A和B成反比例,x=
.
A
2
8
B
0.5
x
9.少先队员每人做好事的件数一定,做好事的总件数与做好事的少先队员人数成正比例.
.
10.表中如果x和y成正比例,那么空格里应填
;如果x和y成反比例,那么空格里应填
.
x
2
6
y
24
11.一种练习本销售的数量与总价的关系如表.
数量/本
1
2
3
4
5
总价/元
5.5
11
16.5
22
27.5
(1)表中有
和
两种相关联的量,总价随着
的变化而变化,且总价与相应数量的比值都是
,实际就是练习本的
.
(2)像这样,两种
的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的
一定,这两种量就叫做
的量,它们的关系叫做
关系.上表中,总价和数量是成
的量,总价与数量成
关系.
12.在比例中,两个外项的积一定,两个两内项成
比例.
三.判断题(共5小题)
13.工作总量一定,工作效率和工作时间成正比例.
(判断对错)
14.在一定的距离内,车轮周长和它转动的圈数成反比例.
.(判断对错)
15.小明应完成的作业量一定,他已完成的作业量和未完成的作业量成反比例.
(判断对错)
16.式子=k(一定)表示的是正比例关系.
.(判断对错)
17.如果a和b成正比例,b和c成反比例,那么a和c一定成反比例.
.(判断对错)
四.应用题(共3小题)
18.淘淘家在装修房屋时,买了同样大小的地板砖,铺地面积与所需块数的关系如图.他家的客厅面积是36m2,需要铺多少块这样的地板砖?(用比例解决问题)
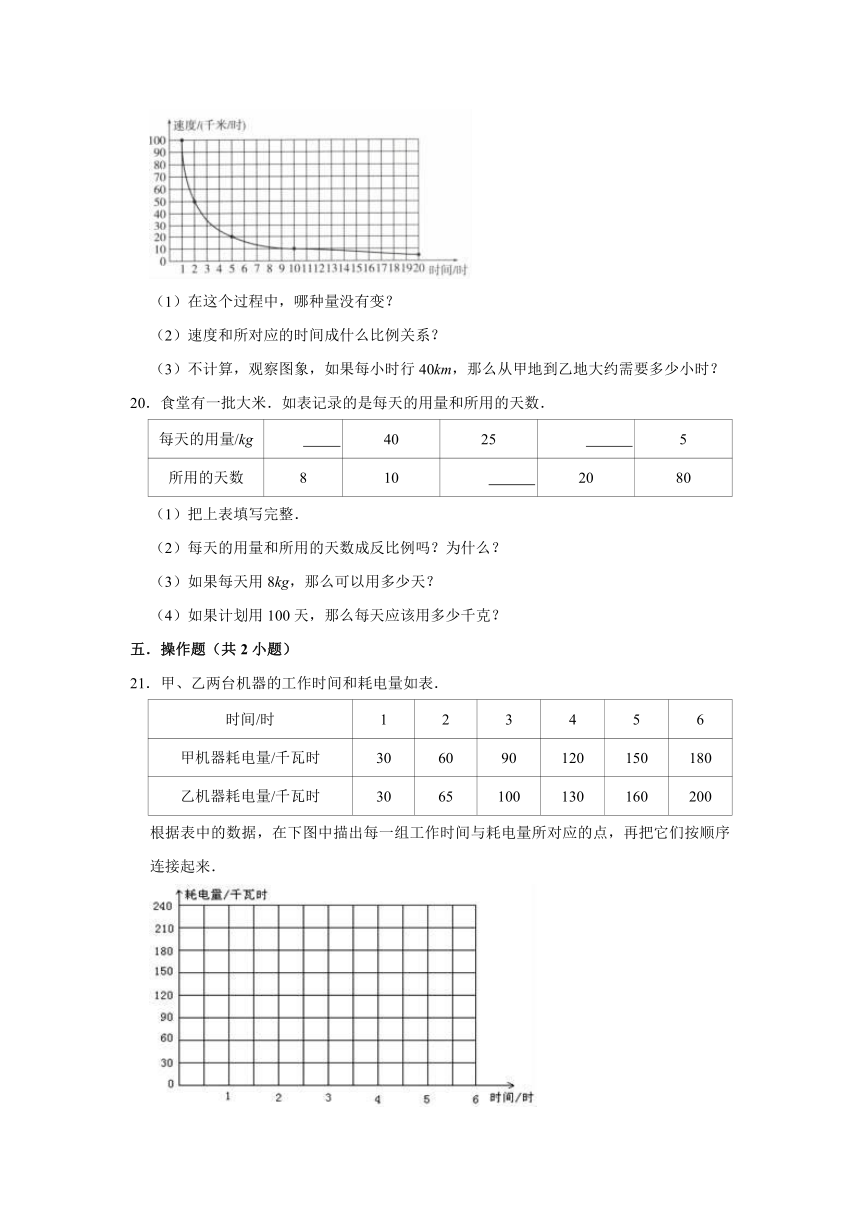
19.下面的图象表示小强从甲地到乙地不同的速度和所对应的时间.
(1)在这个过程中,哪种量没有变?
(2)速度和所对应的时间成什么比例关系?
(3)不计算,观察图象,如果每小时行40km,那么从甲地到乙地大约需要多少小时?
20.食堂有一批大米.如表记录的是每天的用量和所用的天数.
每天的用量/kg
40
25
5
所用的天数
8
10
20
80
(1)把上表填写完整.
(2)每天的用量和所用的天数成反比例吗?为什么?
(3)如果每天用8kg,那么可以用多少天?
(4)如果计划用100天,那么每天应该用多少千克?
五.操作题(共2小题)
21.甲、乙两台机器的工作时间和耗电量如表.
时间/时
1
2
3
4
5
6
甲机器耗电量/千瓦时
30
60
90
120
150
180
乙机器耗电量/千瓦时
30
65
100
130
160
200
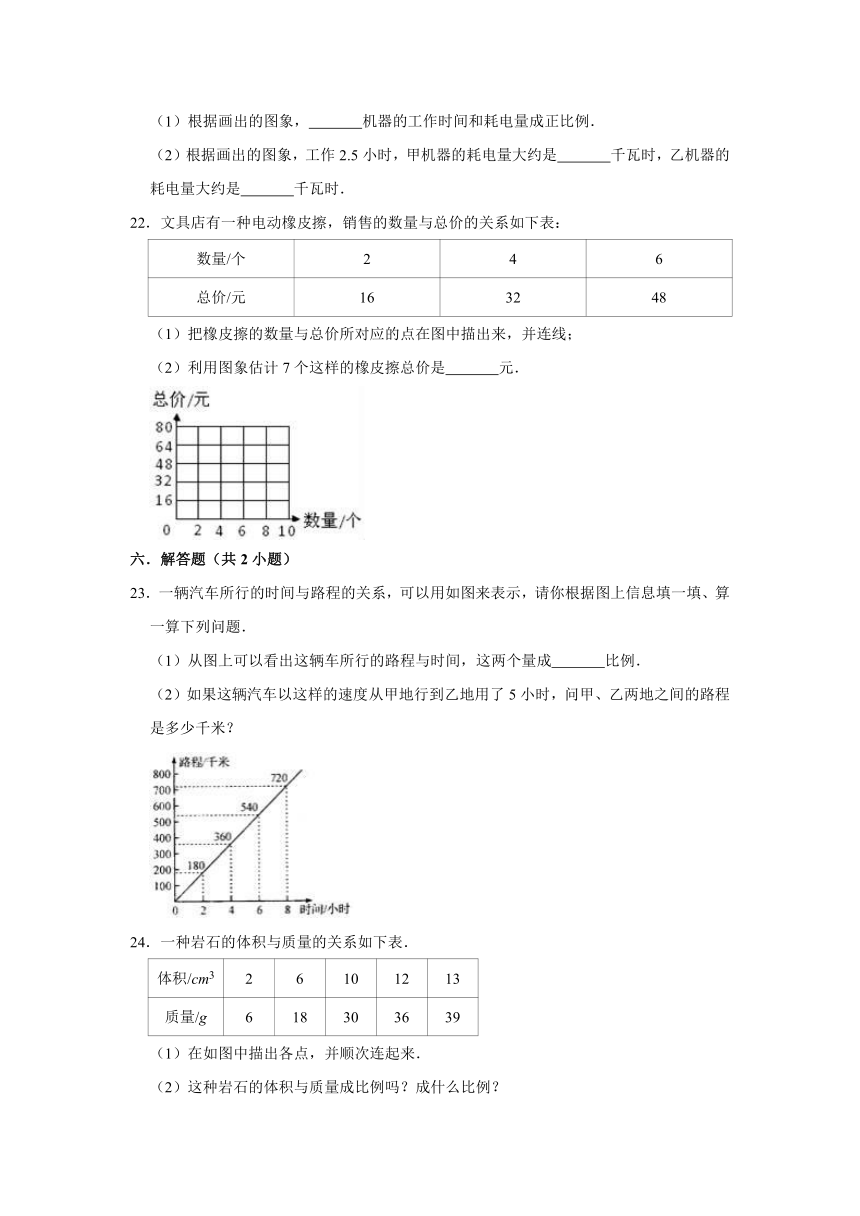
根据表中的数据,在下图中描出每一组工作时间与耗电量所对应的点,再把它们按顺序连接起来.
(1)根据画出的图象,
机器的工作时间和耗电量成正比例.
(2)根据画出的图象,工作2.5小时,甲机器的耗电量大约是
千瓦时,乙机器的耗电量大约是
千瓦时.
22.文具店有一种电动橡皮擦,销售的数量与总价的关系如下表:
数量/个
2
4
6
总价/元
16
32
48
(1)把橡皮擦的数量与总价所对应的点在图中描出来,并连线;
(2)利用图象估计7个这样的橡皮擦总价是
元.
六.解答题(共2小题)
23.一辆汽车所行的时间与路程的关系,可以用如图来表示,请你根据图上信息填一填、算一算下列问题.
(1)从图上可以看出这辆车所行的路程与时间,这两个量成
比例.
(2)如果这辆汽车以这样的速度从甲地行到乙地用了5小时,问甲、乙两地之间的路程是多少千米?
24.一种岩石的体积与质量的关系如下表.
体积/cm3
2
6
10
12
13
质量/g
6
18
30
36
39
(1)在如图中描出各点,并顺次连起来.
(2)这种岩石的体积与质量成比例吗?成什么比例?
(3)如果一块岩石的体积是8cm2,那么这块岩石的质量是多少克?
参考答案与试题解析
一.选择题(共6小题)
1.【分析】判断两个相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,由此逐一分析即可解答.
【解答】解:A,因为2a=5b,所以=(一定),所以a、b成正比例;
B,因为a×7=,所以=14(一定),所以a、b成正比例;
C,因为a×=1,所以ab=3(一定),所以a、b成反比例;
故选:C.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断.
2.【分析】判断两种相关联的量之间是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例.
【解答】解:A.圆的面积=π×圆的半径2,不符合正比例的意义,
所以圆的半径和圆的面积不成正比例关系;
B.因为写字总时间=写字总数×写一个字所用时间,
所以写字总时间÷写一个字所用时间=写字总数(一定)符合正比例的意义,写字总数一定,写一个字所用时间和写字总时间成正比例关系;
C.因为每分钟写字个数×写字总时间=写字总数(一定),符合反比例的意义,不符合正比例的意义,
所以写字总数一定,每分钟写字个数和写字总时间不成正比例关系;
D.两个互相咬合的齿轮,齿轮的齿数是一定的与转数没关系,不符合正比例的意义,
所以两个互相咬合的齿轮,齿轮的齿数和转数不成正比例关系,
故选:B。
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断.
3.【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做成正比例关系.
【解答】解:圆的周长公式:C=πd,
可以推出:C:d=π(一定);
圆的周长和直径是两种相关联的量,圆的周长随直径的变化而变化,π一定,也就是圆的周长和对应的直径的比值一定,所以圆的周长和直径是成正比例关系.
故选:A。
【点评】此题重点考查辨识成正比例的量与成反比例的量、圆的周长和直径的比值为圆周率.
4.【分析】判断a和b是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例.
【解答】解:A、5a=4b,所以a:b=4:5=(一定);不符合反比例的意义,所以a与b不成反比例;
B、=,所以a:b=(一定),不符合反比例的意义,所以a与b不成反比例;
C、5a=,所以ab=(一定),符合反比例的意义,所以a与b成反比例;
D、5a=b+4,5a﹣b=4,不符合反比例的意义,所以a与b不成反比例;
故选:C.
【点评】此题属于辨识成反比例的量,就看这两种量是否是对应的乘积一定,再做出判断.
5.【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例.
【解答】解:因为ab=3(值一定),
则a和b成反比例;
故选:B.
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断.
6.【分析】根据正反比例的意义,分析数量关系,总价是一定的,然后看单价和数量是比值一定还是乘积一定,从而判定成什么比例关系.
【解答】解:从题中可以得到以下数量关系:
单价×数量=总价(一定),
可以看出,单价和数量是两种相关联的量,单价随数量的变化而变化.总价一定,也就是单价与数量相对应数的乘积一定,符合反比例的意义.所以单价与数量成反比例关系.
故选:B。
【点评】此题重点考查正比例和反比例的意义.
二.填空题(共6小题)
7.【分析】判断两种量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,据此解答.
【解答】解:(1)C÷A=B(一定),是比值一定,A和C成正比例;
(2)A×B=C(一定),是乘积一定,A和B成反比例.
故答案为:正比例,反比例.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断.
8.【分析】如果两个相关联的量之间成正比例,那么它们对应的比值一定;如果两个相关联的量之间成反比例,那么它们的乘积一定.
【解答】解:如果A和B成正比例,那么=,根据比例的基本性质,求出x=2;
如果A和B成反比例,那么2×0.5=8x,求出x=0.125.
故答案为:2,0.125.
【点评】本题主要根据成正比例的两个量,它们的比值一定;成反比例的两个量,它们的乘积一定进行解答.
9.【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例.
【解答】解:做好事的总件数÷做好事的少先队员人数=每人做好事的件数(一定),是比值一定,所以成正比例;
故答案为:√.
【点评】此题属于根据正、反比例的意义,判断两种相关联的量是成正比例还是成反比例,就看两种量是对应的比值一定,还是对应的乘积一定,再做出解答.
10.【分析】因为x和y成正比例,所以x:y的比值一定,则2:24=6:y,由此求出y的值;因为x和y成反比例,所以x与y的乘积是一定的,所以2×24=6y,由此求出y的值.
【解答】解:2:24=6:y
2y=24×6
y=24×3
y=72
答:如果x和y成正比例,那么空格里应填72.
2×24=6y
6y=48
y=8
答:如果x和y成反比例,那么空格里应填8.
故答案为:72,8.
【点评】本题主要是根据正、反比例的意义解决问题.
11.【分析】(1)观察表格,发现表中有总价和数量两种相关联的量,总价随着数量的变化而变化,且总价与相应数量的比值都是一定的,实际就是练习本的单价.
(2)像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.上表中,总价和数量是成正比例的量,总价与数量成正比例关系.据此解答.
【解答】解:(1)5.5:1=5.5
11:2=5.5
16.5:3=5.5
22:4=5.5
27.5:5=5.5
表中有总价和数量两种相关联的量,总价随着数量的变化而变化,且总价与相应数量的比值都是一定的,实际就是练习本的单价.
(2)像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.上表中,总价和数量是成正比例的量,总价与数量成正比例关系.
故答案为:总价,数量,数量,一定的,单价,相关联,比值,正比例,正比例,正比例,正比例.
【点评】此题主要考查正比例的意义以及总价、数量和单价之间的关系,正比例的意义是:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系是正比例关系.
12.【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系.
【解答】解:内项×内项=外项×外项(一定),
可以看出,两内项是两种相关联的量,一内项随另一内项的变化而变化,
两外项的积一定,也就是两内项相对应数的乘积一定,所以两内项成反比例关系.
故答案为:反.
【点评】此题重点考查正比例和反比例的意义.
三.判断题(共5小题)
13.【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:因为工作效率×工作时间=工作总量(一定)
乘积一定,工作效率和工作时间成反比例,不成正比例.
故答案为:×.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
14.【分析】判断车轮周长和它转动的圈数是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定,就不成反比例.
【解答】解:车轮周长×它转动的圈数=距离(一定),是乘积一定,车轮周长和它转动的圈数就成反比例.
故判断为:正确.
【点评】此题属于辨识成反比例的量,就看这两种量是否是对应的乘积一定,再做出判断.
15.【分析】根据正反比例的意义,分析数量关系.既然小明应完成的作业量一定,就看那两个变量(他已完成的作业量和未完成的作业量)是比值一定还是乘积一定,从而判定是不是成反比例关系.
【解答】解:已完成的作业量+未完成的作业量=应完成的作业量(一定),
可以看出,已完成的作业量和未完成的作业量是两种相关联的变化的量,但是它们相对应的数是和一定,它们的乘积和比值都不一定,
所以已完成的作业量和未完成的作业量不成任何比例关系.
故答案为:×.
【点评】此题重点考查正比例和反比例的意义.
16.【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:因为=k(一定),所以这是表示x、y成正比例的式子.
故答案为:√.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
17.【分析】根据a和b成正比例,可知a:b=k1(一定),则b=;根据b和c成反比例,可知bc=k2(一定),把b=代入式子bc=k2,即可得出a和c是对应的乘积一定,从而得解.
【解答】解:因为a和b成正比例,所以a:b=k1(一定),则b=,
因为b和c成反比例,所以bc=k2(一定),
把b=代入式子bc=k2(一定),
得:×c=k2(一定),
ac=k1
k2(一定),是a和c对应的乘积一定,所以a和c成反比例.
故答案为:√.
【点评】解决此题关键是根据两种相关联的量成正比例,比值一定,成反比例,乘积一定来解答的.
四.应用题(共3小题)
18.【分析】根据图表可知,铺2平方米用8块地板砖,铺6平方米用24块地板砖,8÷2=24÷6=4(一定),那么铺地面积与所需块数成正比例关系;设需要铺x块这样的地板砖,可得36:x=2:8,然后再根据比例的基本性质进行解答.
【解答】解:根据题意与分析可得:铺地面积与所需块数成正比例关系;
设需要铺x块这样的地板砖,根据题意,可得:
36:x=2:8
2x=36×8
2x÷2=36×8÷2
x=144
答:需要铺144块这样的地板砖.
【点评】本题关键是根据图表得出铺地面积与所需块数成正比例关系,然后再根据比例的意义和性质进行解答.
19.【分析】(1)图中标出5个点:速度是100时时间是1,速度是50时时间是2,速度是20时时间是5,速度是10时时间是10,速度是5时时间是20,由此得出路程没有变化.
(2)观察图象发现速度和时间的关系是反比例关系.
(3)观察图象,如果每小时行40km,那么从甲地到乙地大约需要2.5小时.
【解答】解:(1)图中标出5个点:速度是100时时间是1,速度是50时时间是2,速度是20时时间是5,速度是10时时间是10,速度是5时时间是20,由此得出路程没有变化.
(2)观察图象发现速度和时间的关系是反比例关系.
(3)观察图象,如果每小时行40km,那么从甲地到乙地大约需要2.5小时.
【点评】此题主要考查反比例的意义.解题的关键是掌握反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.
20.【分析】(1)大米总量为40×10=400(kg),分别用每天的用量×所用的天数=大米总量的变形求出每天的用量或所用的天数,计算后填完整表格;
(2)从上表发现每天的用量与所用的天数成反比例关系;因为每天的用量与所用的天数的乘积是一个定值;
(3)因为400÷8=50(天).可以用50天;
(4)因为400÷100=4(kg).每天应该用4千克.
【解答】解:(1)
每天的用量/kg
50
40
25
20
5
所用的天数
8
10
16
20
80
(2)每天的用量与所用的天数成反比例关系;因为每天的用量与所用的天数的乘积是一个定值;
(3)400÷8=50(天);
答:可以用50天;
(4)400÷100=4(kg);
答:每天应该用4千克.
【点评】解答此题的关键是:弄清楚哪两种量成何比例,于是列比例即可求解.
五.操作题(共2小题)
21.【分析】先根据统计表中数据,先分别进行描点,再按图示进行依次连线即可;
(1)根据画出的图象,折线在上升过程中成直线上升的就是机器的工作时间和耗电量成正比例的量.进而判定;
(2)根据画出的图象估计,工作时间在2小时与3小时中间对应的耗电量,就是甲或乙工作2.5小时各自耗电量.
【解答】解:先根据统计表中数据,先分别进行描点,再按图示进行依次连线即可;如图:
(1)根据画出的图象,折线在上升过程中各点的连线成一条直线上升的就是机器的工作时间和耗电量成正比例的量,所以甲机器的工作时间和耗电量成正比例,
(2)根据画出的图象估计,工作时间在2小时与3小时中间对应的耗电量,就是甲或乙工作2.5小时各自耗电量;
所以:甲工作2.5小时耗电量:大约75千瓦时,乙工作2.5小时耗电量:大约82.5千瓦时,
故答案为:甲;75,82.5.
【点评】本题考查的根据统计表中数据画折线统计图的方法的运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.
22.【分析】(1)根据表中的数据,在统计图中描出数量和总价所对应的点,再把它们按顺序连起来;
(2)根据单价×数量=总价进行解答.
【解答】解:(1)连线如下:
(2)16÷2×7
=8×7
=56(元);
答:7个这样的橡皮擦总价是56元.
故答案为:56.
【点评】解答此题的关键利用图中已知的信息,结合给出的条件,求得各部分数据解决问题.
六.解答题(共2小题)
23.【分析】(1)根据正比例的意义和反比例的意义进行解答即可;
(2)先根据“路程÷时间=速度”求出汽车的速度,进而根据“速度×时间=路程”进行解答即可.
【解答】解:(1)表示时间和路程关系的图象是一条直线,是正比例图象,所以这两个量成正比例;
(2)180÷2×5=450(千米);
答:甲、乙两地之间的路程是450千米.
故答案为:正.
【点评】解答此题的关键是:(1)看两种相关联量是比值一定还是乘积一定,如乘积一定,则两种量成反比例;如比值一定,则两种量成正比例;(2)根据路程、时间和速度三者之间的关系,进行解答.
24.【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.用字母表示是=k(一定).
(1)先描出五个点的位置,然后顺次连线即可.
(2)计算出五组数据的比值,看比值是否为定值即可.
(3)利用比值为定值,直接计算岩石的质量即可.
【解答】解:(1)
(2)因为=3;=3;=3;=3;=3
它们的比值一定,都等于3,
所以这种岩石的体积与质量成比例,成正比例.
(3)8×3=24(克)
答:如果一块岩石的体积是8cm3,那么这块岩石的质量是24克.
【点评】此题考查成正比例量的定义、图象及应用,理解成正比例量的含义是解题的关键.
比例
第2课时
正比例和反比例》同步测试题
一.选择题(共6小题)
1.下列等式中,a与b(a、b均不为0)成反比例的是( )
A.2a=5b
B.a×7=
C.a×=1
2.下列两种量的关系成正比例关系的是( )
A.圆的半径和圆的面积
B.写字总数一定,写一个字所用时间和写字总时间
C.写字总数一定,每分钟写字个数和写字总时间
D.两个互相咬合的齿轮,齿轮的齿数和转数
3.圆的周长和直径( )
A.成正比例
B.成反比例
C.不成比例
4.a和b成反比例关系的式子是( )
A.5a=4b
B.=
C.5a=
D.5a=b+4
5.如果ab=3,那么a与b( )
A.不成比例
B.成反比例
C.成正比例
6.总价一定,单价和数量( )
A.成正比例
B.成反比例
C.不成比例
D.以上都不对
二.填空题(共6小题)
7.A、B、C三量的关系时A×B=C中,当C一定时,A和B成
关系.
8.表格中,如果A和B成正比例,x=
,如果A和B成反比例,x=
.
A
2
8
B
0.5
x
9.少先队员每人做好事的件数一定,做好事的总件数与做好事的少先队员人数成正比例.
.
10.表中如果x和y成正比例,那么空格里应填
;如果x和y成反比例,那么空格里应填
.
x
2
6
y
24
11.一种练习本销售的数量与总价的关系如表.
数量/本
1
2
3
4
5
总价/元
5.5
11
16.5
22
27.5
(1)表中有
和
两种相关联的量,总价随着
的变化而变化,且总价与相应数量的比值都是
,实际就是练习本的
.
(2)像这样,两种
的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的
一定,这两种量就叫做
的量,它们的关系叫做
关系.上表中,总价和数量是成
的量,总价与数量成
关系.
12.在比例中,两个外项的积一定,两个两内项成
比例.
三.判断题(共5小题)
13.工作总量一定,工作效率和工作时间成正比例.
(判断对错)
14.在一定的距离内,车轮周长和它转动的圈数成反比例.
.(判断对错)
15.小明应完成的作业量一定,他已完成的作业量和未完成的作业量成反比例.
(判断对错)
16.式子=k(一定)表示的是正比例关系.
.(判断对错)
17.如果a和b成正比例,b和c成反比例,那么a和c一定成反比例.
.(判断对错)
四.应用题(共3小题)
18.淘淘家在装修房屋时,买了同样大小的地板砖,铺地面积与所需块数的关系如图.他家的客厅面积是36m2,需要铺多少块这样的地板砖?(用比例解决问题)
19.下面的图象表示小强从甲地到乙地不同的速度和所对应的时间.
(1)在这个过程中,哪种量没有变?
(2)速度和所对应的时间成什么比例关系?
(3)不计算,观察图象,如果每小时行40km,那么从甲地到乙地大约需要多少小时?
20.食堂有一批大米.如表记录的是每天的用量和所用的天数.
每天的用量/kg
40
25
5
所用的天数
8
10
20
80
(1)把上表填写完整.
(2)每天的用量和所用的天数成反比例吗?为什么?
(3)如果每天用8kg,那么可以用多少天?
(4)如果计划用100天,那么每天应该用多少千克?
五.操作题(共2小题)
21.甲、乙两台机器的工作时间和耗电量如表.
时间/时
1
2
3
4
5
6
甲机器耗电量/千瓦时
30
60
90
120
150
180
乙机器耗电量/千瓦时
30
65
100
130
160
200
根据表中的数据,在下图中描出每一组工作时间与耗电量所对应的点,再把它们按顺序连接起来.
(1)根据画出的图象,
机器的工作时间和耗电量成正比例.
(2)根据画出的图象,工作2.5小时,甲机器的耗电量大约是
千瓦时,乙机器的耗电量大约是
千瓦时.
22.文具店有一种电动橡皮擦,销售的数量与总价的关系如下表:
数量/个
2
4
6
总价/元
16
32
48
(1)把橡皮擦的数量与总价所对应的点在图中描出来,并连线;
(2)利用图象估计7个这样的橡皮擦总价是
元.
六.解答题(共2小题)
23.一辆汽车所行的时间与路程的关系,可以用如图来表示,请你根据图上信息填一填、算一算下列问题.
(1)从图上可以看出这辆车所行的路程与时间,这两个量成
比例.
(2)如果这辆汽车以这样的速度从甲地行到乙地用了5小时,问甲、乙两地之间的路程是多少千米?
24.一种岩石的体积与质量的关系如下表.
体积/cm3
2
6
10
12
13
质量/g
6
18
30
36
39
(1)在如图中描出各点,并顺次连起来.
(2)这种岩石的体积与质量成比例吗?成什么比例?
(3)如果一块岩石的体积是8cm2,那么这块岩石的质量是多少克?
参考答案与试题解析
一.选择题(共6小题)
1.【分析】判断两个相关联的量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,由此逐一分析即可解答.
【解答】解:A,因为2a=5b,所以=(一定),所以a、b成正比例;
B,因为a×7=,所以=14(一定),所以a、b成正比例;
C,因为a×=1,所以ab=3(一定),所以a、b成反比例;
故选:C.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断.
2.【分析】判断两种相关联的量之间是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例.
【解答】解:A.圆的面积=π×圆的半径2,不符合正比例的意义,
所以圆的半径和圆的面积不成正比例关系;
B.因为写字总时间=写字总数×写一个字所用时间,
所以写字总时间÷写一个字所用时间=写字总数(一定)符合正比例的意义,写字总数一定,写一个字所用时间和写字总时间成正比例关系;
C.因为每分钟写字个数×写字总时间=写字总数(一定),符合反比例的意义,不符合正比例的意义,
所以写字总数一定,每分钟写字个数和写字总时间不成正比例关系;
D.两个互相咬合的齿轮,齿轮的齿数是一定的与转数没关系,不符合正比例的意义,
所以两个互相咬合的齿轮,齿轮的齿数和转数不成正比例关系,
故选:B。
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量是否成正比例,就看这两种量是否是对应的比值一定,再做出判断.
3.【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做成正比例关系.
【解答】解:圆的周长公式:C=πd,
可以推出:C:d=π(一定);
圆的周长和直径是两种相关联的量,圆的周长随直径的变化而变化,π一定,也就是圆的周长和对应的直径的比值一定,所以圆的周长和直径是成正比例关系.
故选:A。
【点评】此题重点考查辨识成正比例的量与成反比例的量、圆的周长和直径的比值为圆周率.
4.【分析】判断a和b是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定或乘积不一定,就不成反比例.
【解答】解:A、5a=4b,所以a:b=4:5=(一定);不符合反比例的意义,所以a与b不成反比例;
B、=,所以a:b=(一定),不符合反比例的意义,所以a与b不成反比例;
C、5a=,所以ab=(一定),符合反比例的意义,所以a与b成反比例;
D、5a=b+4,5a﹣b=4,不符合反比例的意义,所以a与b不成反比例;
故选:C.
【点评】此题属于辨识成反比例的量,就看这两种量是否是对应的乘积一定,再做出判断.
5.【分析】判断两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,如果是其它的量一定或乘积、比值不一定,就不成比例.
【解答】解:因为ab=3(值一定),
则a和b成反比例;
故选:B.
【点评】此题属于根据正、反比例的意义,辨识两种相关联的量成不成比例,成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,还是对应的其它量一定,再做出判断.
6.【分析】根据正反比例的意义,分析数量关系,总价是一定的,然后看单价和数量是比值一定还是乘积一定,从而判定成什么比例关系.
【解答】解:从题中可以得到以下数量关系:
单价×数量=总价(一定),
可以看出,单价和数量是两种相关联的量,单价随数量的变化而变化.总价一定,也就是单价与数量相对应数的乘积一定,符合反比例的意义.所以单价与数量成反比例关系.
故选:B。
【点评】此题重点考查正比例和反比例的意义.
二.填空题(共6小题)
7.【分析】判断两种量成什么比例,就看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,就成反比例,据此解答.
【解答】解:(1)C÷A=B(一定),是比值一定,A和C成正比例;
(2)A×B=C(一定),是乘积一定,A和B成反比例.
故答案为:正比例,反比例.
【点评】此题属于辨识成正、反比例的量,就看这两种量是对应的比值一定,还是对应的乘积一定,再做出判断.
8.【分析】如果两个相关联的量之间成正比例,那么它们对应的比值一定;如果两个相关联的量之间成反比例,那么它们的乘积一定.
【解答】解:如果A和B成正比例,那么=,根据比例的基本性质,求出x=2;
如果A和B成反比例,那么2×0.5=8x,求出x=0.125.
故答案为:2,0.125.
【点评】本题主要根据成正比例的两个量,它们的比值一定;成反比例的两个量,它们的乘积一定进行解答.
9.【分析】判定两种相关联的量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定就成反比例.
【解答】解:做好事的总件数÷做好事的少先队员人数=每人做好事的件数(一定),是比值一定,所以成正比例;
故答案为:√.
【点评】此题属于根据正、反比例的意义,判断两种相关联的量是成正比例还是成反比例,就看两种量是对应的比值一定,还是对应的乘积一定,再做出解答.
10.【分析】因为x和y成正比例,所以x:y的比值一定,则2:24=6:y,由此求出y的值;因为x和y成反比例,所以x与y的乘积是一定的,所以2×24=6y,由此求出y的值.
【解答】解:2:24=6:y
2y=24×6
y=24×3
y=72
答:如果x和y成正比例,那么空格里应填72.
2×24=6y
6y=48
y=8
答:如果x和y成反比例,那么空格里应填8.
故答案为:72,8.
【点评】本题主要是根据正、反比例的意义解决问题.
11.【分析】(1)观察表格,发现表中有总价和数量两种相关联的量,总价随着数量的变化而变化,且总价与相应数量的比值都是一定的,实际就是练习本的单价.
(2)像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.上表中,总价和数量是成正比例的量,总价与数量成正比例关系.据此解答.
【解答】解:(1)5.5:1=5.5
11:2=5.5
16.5:3=5.5
22:4=5.5
27.5:5=5.5
表中有总价和数量两种相关联的量,总价随着数量的变化而变化,且总价与相应数量的比值都是一定的,实际就是练习本的单价.
(2)像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.上表中,总价和数量是成正比例的量,总价与数量成正比例关系.
故答案为:总价,数量,数量,一定的,单价,相关联,比值,正比例,正比例,正比例,正比例.
【点评】此题主要考查正比例的意义以及总价、数量和单价之间的关系,正比例的意义是:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系是正比例关系.
12.【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系.
【解答】解:内项×内项=外项×外项(一定),
可以看出,两内项是两种相关联的量,一内项随另一内项的变化而变化,
两外项的积一定,也就是两内项相对应数的乘积一定,所以两内项成反比例关系.
故答案为:反.
【点评】此题重点考查正比例和反比例的意义.
三.判断题(共5小题)
13.【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:因为工作效率×工作时间=工作总量(一定)
乘积一定,工作效率和工作时间成反比例,不成正比例.
故答案为:×.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
14.【分析】判断车轮周长和它转动的圈数是否成反比例,就看这两种量是否是对应的乘积一定,如果是乘积一定,就成反比例,如果不是乘积一定,就不成反比例.
【解答】解:车轮周长×它转动的圈数=距离(一定),是乘积一定,车轮周长和它转动的圈数就成反比例.
故判断为:正确.
【点评】此题属于辨识成反比例的量,就看这两种量是否是对应的乘积一定,再做出判断.
15.【分析】根据正反比例的意义,分析数量关系.既然小明应完成的作业量一定,就看那两个变量(他已完成的作业量和未完成的作业量)是比值一定还是乘积一定,从而判定是不是成反比例关系.
【解答】解:已完成的作业量+未完成的作业量=应完成的作业量(一定),
可以看出,已完成的作业量和未完成的作业量是两种相关联的变化的量,但是它们相对应的数是和一定,它们的乘积和比值都不一定,
所以已完成的作业量和未完成的作业量不成任何比例关系.
故答案为:×.
【点评】此题重点考查正比例和反比例的意义.
16.【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:因为=k(一定),所以这是表示x、y成正比例的式子.
故答案为:√.
【点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
17.【分析】根据a和b成正比例,可知a:b=k1(一定),则b=;根据b和c成反比例,可知bc=k2(一定),把b=代入式子bc=k2,即可得出a和c是对应的乘积一定,从而得解.
【解答】解:因为a和b成正比例,所以a:b=k1(一定),则b=,
因为b和c成反比例,所以bc=k2(一定),
把b=代入式子bc=k2(一定),
得:×c=k2(一定),
ac=k1
k2(一定),是a和c对应的乘积一定,所以a和c成反比例.
故答案为:√.
【点评】解决此题关键是根据两种相关联的量成正比例,比值一定,成反比例,乘积一定来解答的.
四.应用题(共3小题)
18.【分析】根据图表可知,铺2平方米用8块地板砖,铺6平方米用24块地板砖,8÷2=24÷6=4(一定),那么铺地面积与所需块数成正比例关系;设需要铺x块这样的地板砖,可得36:x=2:8,然后再根据比例的基本性质进行解答.
【解答】解:根据题意与分析可得:铺地面积与所需块数成正比例关系;
设需要铺x块这样的地板砖,根据题意,可得:
36:x=2:8
2x=36×8
2x÷2=36×8÷2
x=144
答:需要铺144块这样的地板砖.
【点评】本题关键是根据图表得出铺地面积与所需块数成正比例关系,然后再根据比例的意义和性质进行解答.
19.【分析】(1)图中标出5个点:速度是100时时间是1,速度是50时时间是2,速度是20时时间是5,速度是10时时间是10,速度是5时时间是20,由此得出路程没有变化.
(2)观察图象发现速度和时间的关系是反比例关系.
(3)观察图象,如果每小时行40km,那么从甲地到乙地大约需要2.5小时.
【解答】解:(1)图中标出5个点:速度是100时时间是1,速度是50时时间是2,速度是20时时间是5,速度是10时时间是10,速度是5时时间是20,由此得出路程没有变化.
(2)观察图象发现速度和时间的关系是反比例关系.
(3)观察图象,如果每小时行40km,那么从甲地到乙地大约需要2.5小时.
【点评】此题主要考查反比例的意义.解题的关键是掌握反比例的意义:两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系.
20.【分析】(1)大米总量为40×10=400(kg),分别用每天的用量×所用的天数=大米总量的变形求出每天的用量或所用的天数,计算后填完整表格;
(2)从上表发现每天的用量与所用的天数成反比例关系;因为每天的用量与所用的天数的乘积是一个定值;
(3)因为400÷8=50(天).可以用50天;
(4)因为400÷100=4(kg).每天应该用4千克.
【解答】解:(1)
每天的用量/kg
50
40
25
20
5
所用的天数
8
10
16
20
80
(2)每天的用量与所用的天数成反比例关系;因为每天的用量与所用的天数的乘积是一个定值;
(3)400÷8=50(天);
答:可以用50天;
(4)400÷100=4(kg);
答:每天应该用4千克.
【点评】解答此题的关键是:弄清楚哪两种量成何比例,于是列比例即可求解.
五.操作题(共2小题)
21.【分析】先根据统计表中数据,先分别进行描点,再按图示进行依次连线即可;
(1)根据画出的图象,折线在上升过程中成直线上升的就是机器的工作时间和耗电量成正比例的量.进而判定;
(2)根据画出的图象估计,工作时间在2小时与3小时中间对应的耗电量,就是甲或乙工作2.5小时各自耗电量.
【解答】解:先根据统计表中数据,先分别进行描点,再按图示进行依次连线即可;如图:
(1)根据画出的图象,折线在上升过程中各点的连线成一条直线上升的就是机器的工作时间和耗电量成正比例的量,所以甲机器的工作时间和耗电量成正比例,
(2)根据画出的图象估计,工作时间在2小时与3小时中间对应的耗电量,就是甲或乙工作2.5小时各自耗电量;
所以:甲工作2.5小时耗电量:大约75千瓦时,乙工作2.5小时耗电量:大约82.5千瓦时,
故答案为:甲;75,82.5.
【点评】本题考查的根据统计表中数据画折线统计图的方法的运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.
22.【分析】(1)根据表中的数据,在统计图中描出数量和总价所对应的点,再把它们按顺序连起来;
(2)根据单价×数量=总价进行解答.
【解答】解:(1)连线如下:
(2)16÷2×7
=8×7
=56(元);
答:7个这样的橡皮擦总价是56元.
故答案为:56.
【点评】解答此题的关键利用图中已知的信息,结合给出的条件,求得各部分数据解决问题.
六.解答题(共2小题)
23.【分析】(1)根据正比例的意义和反比例的意义进行解答即可;
(2)先根据“路程÷时间=速度”求出汽车的速度,进而根据“速度×时间=路程”进行解答即可.
【解答】解:(1)表示时间和路程关系的图象是一条直线,是正比例图象,所以这两个量成正比例;
(2)180÷2×5=450(千米);
答:甲、乙两地之间的路程是450千米.
故答案为:正.
【点评】解答此题的关键是:(1)看两种相关联量是比值一定还是乘积一定,如乘积一定,则两种量成反比例;如比值一定,则两种量成正比例;(2)根据路程、时间和速度三者之间的关系,进行解答.
24.【分析】两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系.用字母表示是=k(一定).
(1)先描出五个点的位置,然后顺次连线即可.
(2)计算出五组数据的比值,看比值是否为定值即可.
(3)利用比值为定值,直接计算岩石的质量即可.
【解答】解:(1)
(2)因为=3;=3;=3;=3;=3
它们的比值一定,都等于3,
所以这种岩石的体积与质量成比例,成正比例.
(3)8×3=24(克)
答:如果一块岩石的体积是8cm3,那么这块岩石的质量是24克.
【点评】此题考查成正比例量的定义、图象及应用,理解成正比例量的含义是解题的关键.
