2020-2021学年北师大版八年级数学下册 1.3.2 线段的垂直平分线(二) 同步练习题(word含答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册 1.3.2 线段的垂直平分线(二) 同步练习题(word含答案) | 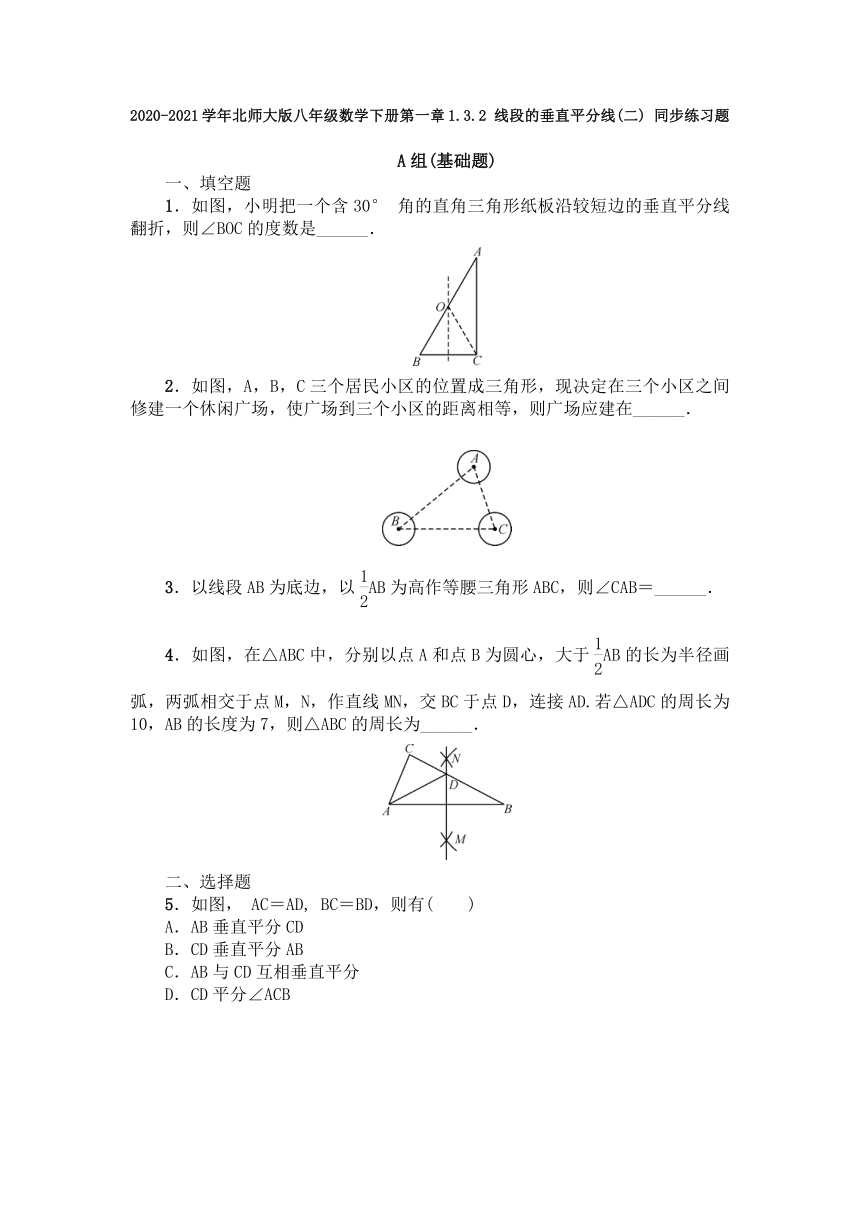 | |
| 格式 | docx | ||
| 文件大小 | 110.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-14 11:23:35 | ||
图片预览


文档简介
2020-2021学年北师大版八年级数学下册第一章1.3.2
线段的垂直平分线(二)
同步练习题
A组(基础题)
一、填空题
1.如图,小明把一个含30°
角的直角三角形纸板沿较短边的垂直平分线翻折,则∠BOC的度数是______.
2.如图,A,B,C三个居民小区的位置成三角形,现决定在三个小区之间修建一个休闲广场,使广场到三个小区的距离相等,则广场应建在______.
3.以线段AB为底边,以AB为高作等腰三角形ABC,则∠CAB=______.
4.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB的长度为7,则△ABC的周长为______.
二、选择题
5.如图,
AC=AD,
BC=BD,则有(
)
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
6.为了丰富学生的课余生活,某校举行联欢晚会,在联欢晚会上,有A,B,C三名同学站在一个三角形三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,凳子应放在△ABC的(
)
A.三边中线的交点处
B.三条角平分线的交点处
C.三边高的交点处
D.三边垂直平分线的交点处
7.过直线l外一点P作l的垂线,先在直线l上取两点A,B,使PA=PB,再作(
)
A.线段AB的垂线
B.∠PAB的平分线
C.∠PBA的平分线
D.∠APB的平分线
8.如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是(
)
A.l是线段EH的垂直平分线
B.l是线段EQ的垂直平分线
C.l是线段FH的垂直平分线
D.EH是l的垂直平分线
三、解答题
9.(1)如图,已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:AD垂直平分EF.
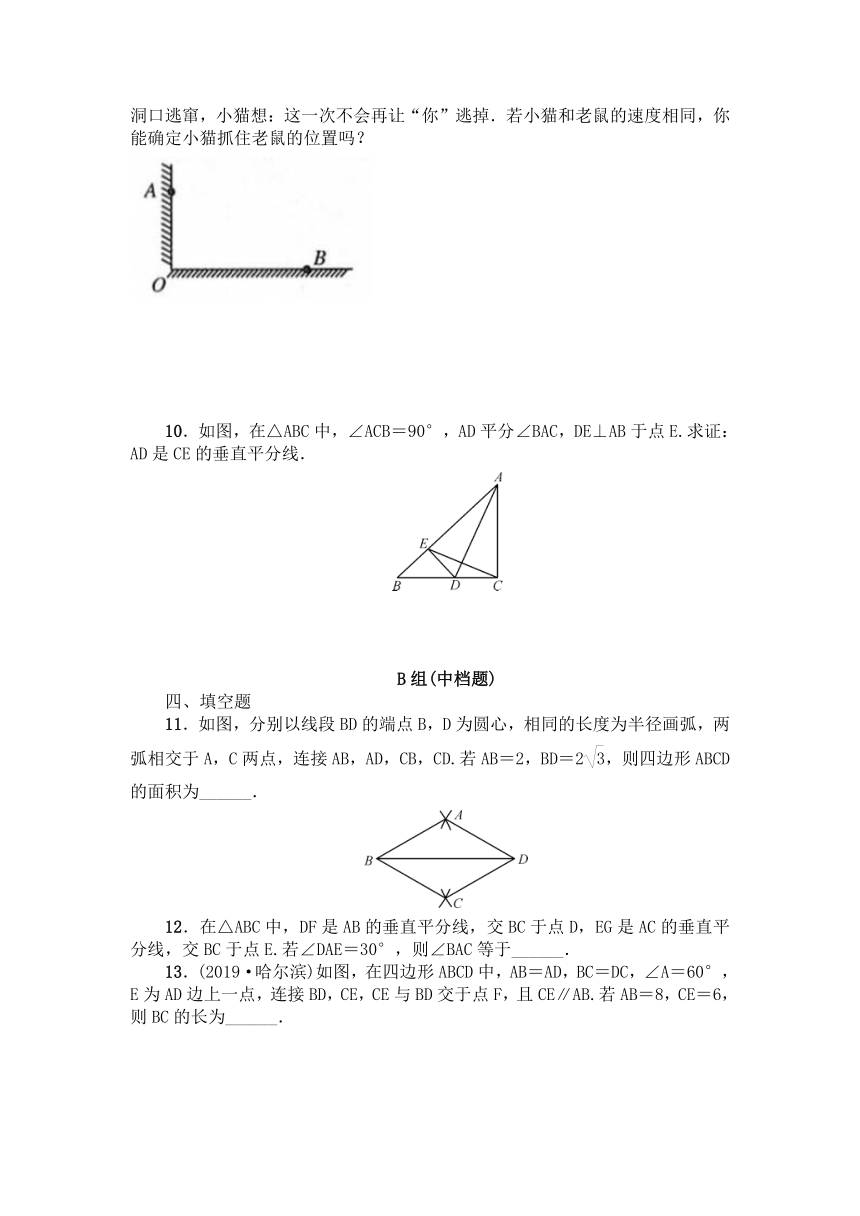
(2)如图,在墙角点O处有一个老鼠洞,小猫在点A处发现老鼠从点B处往洞口逃窜,小猫想:这一次不会再让“你”逃掉.若小猫和老鼠的速度相同,你能确定小猫抓住老鼠的位置吗?
10.如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E.求证:AD是CE的垂直平分线.
B组(中档题)
四、填空题
11.如图,分别以线段BD的端点B,D为圆心,相同的长度为半径画弧,两弧相交于A,C两点,连接AB,AD,CB,CD.若AB=2,BD=2,则四边形ABCD的面积为______.
12.在△ABC中,DF是AB的垂直平分线,交BC于点D,EG是AC的垂直平分线,交BC于点E.若∠DAE=30°,则∠BAC等于______.
13.(2019·哈尔滨)如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,
E为AD边上一点,连接BD,CE,CE与BD交于点F,且CE∥AB.若AB=8,CE=6,则BC的长为______.
五、解答题
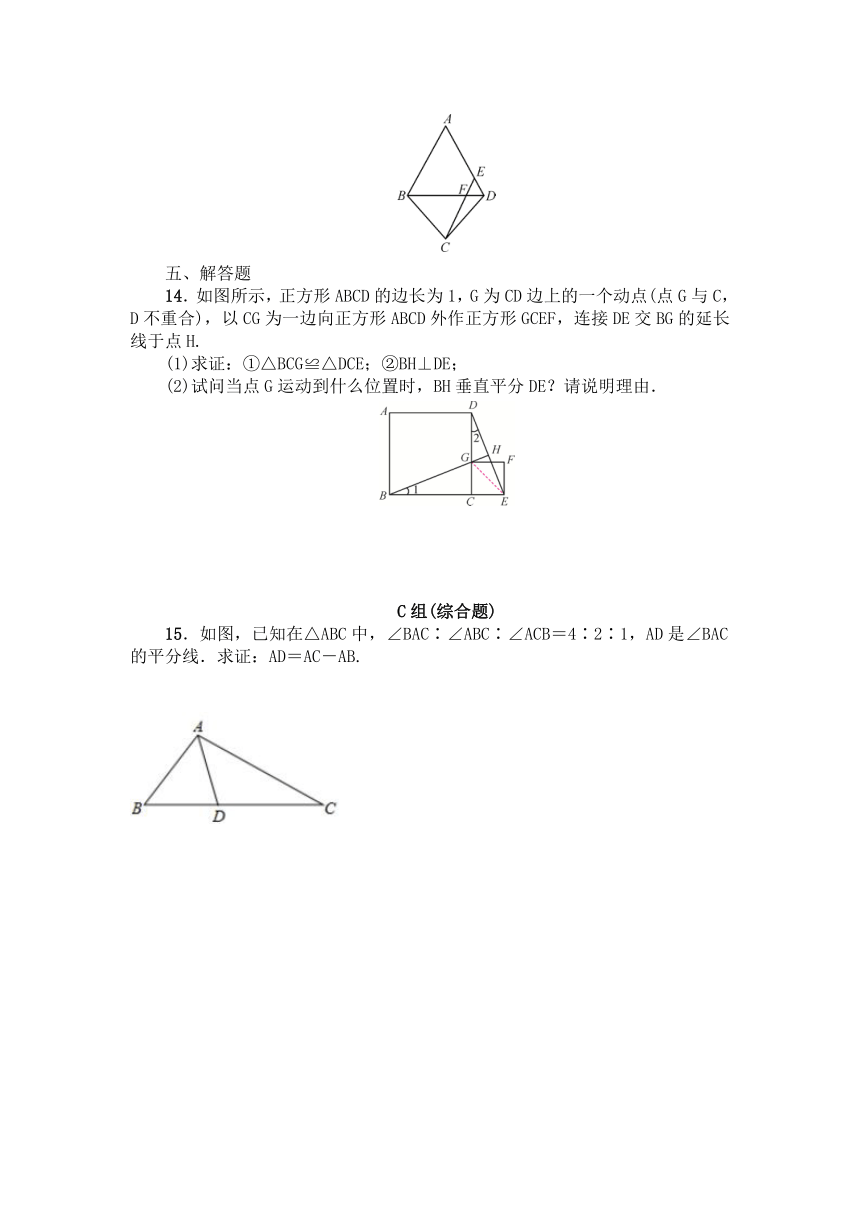
14.如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C,D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.
(1)求证:①△BCG≌△DCE;②BH⊥DE;
(2)试问当点G运动到什么位置时,BH垂直平分DE?请说明理由.
C组(综合题)
15.如图,已知在△ABC中,∠BAC∶∠ABC∶∠ACB=4∶2∶1,AD是∠BAC的平分线.求证:AD=AC-AB.
参考答案
2020-2021学年北师大版八年级数学下册第一章1.3.2
线段的垂直平分线(二)
同步练习题
A组(基础题)
一、填空题
1.如图,小明把一个含30°
角的直角三角形纸板沿较短边的垂直平分线翻折,则∠BOC的度数是60°.
2.如图,A,B,C三个居民小区的位置成三角形,现决定在三个小区之间修建一个休闲广场,使广场到三个小区的距离相等,则广场应建在三边垂直平分线的交点处.
3.以线段AB为底边,以AB为高作等腰三角形ABC,则∠CAB=45°.
4.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB的长度为7,则△ABC的周长为17.
二、选择题
5.如图,
AC=AD,
BC=BD,则有(A)
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
6.为了丰富学生的课余生活,某校举行联欢晚会,在联欢晚会上,有A,B,C三名同学站在一个三角形三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,凳子应放在△ABC的(D)
A.三边中线的交点处
B.三条角平分线的交点处
C.三边高的交点处
D.三边垂直平分线的交点处
7.过直线l外一点P作l的垂线,先在直线l上取两点A,B,使PA=PB,再作(D)
A.线段AB的垂线
B.∠PAB的平分线
C.∠PBA的平分线
D.∠APB的平分线
8.如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是(A)
A.l是线段EH的垂直平分线
B.l是线段EQ的垂直平分线
C.l是线段FH的垂直平分线
D.EH是l的垂直平分线
三、解答题
9.(1)如图,已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:AD垂直平分EF.
证明:∵AD是△ABC的角平分线,
DE⊥AB,DF⊥AC,
∴DE=DF.
∴Rt△AED≌Rt△AFD.∴AE=AF.
∵AD是等腰△AEF的顶角平分线,
∴AD垂直平分EF.
(2)如图,在墙角点O处有一个老鼠洞,小猫在点A处发现老鼠从点B处往洞口逃窜,小猫想:这一次不会再让“你”逃掉.若小猫和老鼠的速度相同,你能确定小猫抓住老鼠的位置吗?
解:如图,连接AB,作线段AB的垂直平分线,交OB于点P,则小猫在点P处抓住老鼠.
10.如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E.求证:AD是CE的垂直平分线.
证明:∵∠ACB=90°,AD平分∠BAC,DE⊥AB,
∴DE=DC.
∴点D在线段CE的垂直平分线上.
∵∠EAD=∠CAD,∠AED=∠ACD=90°,DE=DC,
∴△AED≌△ACD(AAS).∴AE=AC.
∴点A在线段CE的垂直平分线上.
∴直线AD是CE的垂直平分线.
B组(中档题)
四、填空题
11.如图,分别以线段BD的端点B,D为圆心,相同的长度为半径画弧,两弧相交于A,C两点,连接AB,AD,CB,CD.若AB=2,BD=2,则四边形ABCD的面积为2.
12.在△ABC中,DF是AB的垂直平分线,交BC于点D,EG是AC的垂直平分线,交BC于点E.若∠DAE=30°,则∠BAC等于75°或105°.
13.(2019·哈尔滨)如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,
E为AD边上一点,连接BD,CE,CE与BD交于点F,且CE∥AB.若AB=8,CE=6,则BC的长为2.
五、解答题
14.如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C,D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.
(1)求证:①△BCG≌△DCE;②BH⊥DE;
(2)试问当点G运动到什么位置时,BH垂直平分DE?请说明理由.
解:(1)证明:在正方形ABCD中,∠BCG=90°,BC=CD,
在正方形GCEF中,∠DCE=90°,CG=CE,
在△BCG和△DCE中,
∴△BCG≌△DCE(SAS).
∴∠1=∠2.
∵∠2+∠DEC=90°,
∴∠1+∠DEC=90°.
∴∠BHD=90°.
∴BH⊥DE.
(2)当GC=-1时,BH垂直平分DE.理由如下:
连接EG.
∵BH垂直平分DE.
∴EG=DG.
设CG=x,则CE=CG=x.
∵∠DCE=90°,
∴EG=x,DG=x.
∵DG+CG=CD,
∴x+x=1,解得x=-1.
∴当GC=-1时,BH垂直平分DE.
C组(综合题)
15.如图,已知在△ABC中,∠BAC∶∠ABC∶∠ACB=4∶2∶1,AD是∠BAC的平分线.求证:AD=AC-AB.
证明:在AC上截取AE=AB,连接DE,设∠C=x.
∵∠BAC∶∠ABC∶∠ACB=4∶2∶1,
∴∠BAC=4x,∠B=2x.
∵AD是∠BAC的平分线,∴∠BAD=∠DAE=2x.
在△ABD和△AED中,
∴△ABD≌△AED(SAS).∴∠B=∠AED=2x.
∴∠AED=∠DAE.∴DA=DE.
∵∠AED=∠EDC+∠C,∠C=x,
∴∠EDC=2x-x=x,即∠EDC=∠C,
∴ED=EC.∴DA=EC.
∴AC=AE+EC=AB+AD,即AD=AC-AB.
线段的垂直平分线(二)
同步练习题
A组(基础题)
一、填空题
1.如图,小明把一个含30°
角的直角三角形纸板沿较短边的垂直平分线翻折,则∠BOC的度数是______.
2.如图,A,B,C三个居民小区的位置成三角形,现决定在三个小区之间修建一个休闲广场,使广场到三个小区的距离相等,则广场应建在______.
3.以线段AB为底边,以AB为高作等腰三角形ABC,则∠CAB=______.
4.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB的长度为7,则△ABC的周长为______.
二、选择题
5.如图,
AC=AD,
BC=BD,则有(
)
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
6.为了丰富学生的课余生活,某校举行联欢晚会,在联欢晚会上,有A,B,C三名同学站在一个三角形三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,凳子应放在△ABC的(
)
A.三边中线的交点处
B.三条角平分线的交点处
C.三边高的交点处
D.三边垂直平分线的交点处
7.过直线l外一点P作l的垂线,先在直线l上取两点A,B,使PA=PB,再作(
)
A.线段AB的垂线
B.∠PAB的平分线
C.∠PBA的平分线
D.∠APB的平分线
8.如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是(
)
A.l是线段EH的垂直平分线
B.l是线段EQ的垂直平分线
C.l是线段FH的垂直平分线
D.EH是l的垂直平分线
三、解答题
9.(1)如图,已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:AD垂直平分EF.
(2)如图,在墙角点O处有一个老鼠洞,小猫在点A处发现老鼠从点B处往洞口逃窜,小猫想:这一次不会再让“你”逃掉.若小猫和老鼠的速度相同,你能确定小猫抓住老鼠的位置吗?
10.如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E.求证:AD是CE的垂直平分线.
B组(中档题)
四、填空题
11.如图,分别以线段BD的端点B,D为圆心,相同的长度为半径画弧,两弧相交于A,C两点,连接AB,AD,CB,CD.若AB=2,BD=2,则四边形ABCD的面积为______.
12.在△ABC中,DF是AB的垂直平分线,交BC于点D,EG是AC的垂直平分线,交BC于点E.若∠DAE=30°,则∠BAC等于______.
13.(2019·哈尔滨)如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,
E为AD边上一点,连接BD,CE,CE与BD交于点F,且CE∥AB.若AB=8,CE=6,则BC的长为______.
五、解答题
14.如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C,D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.
(1)求证:①△BCG≌△DCE;②BH⊥DE;
(2)试问当点G运动到什么位置时,BH垂直平分DE?请说明理由.
C组(综合题)
15.如图,已知在△ABC中,∠BAC∶∠ABC∶∠ACB=4∶2∶1,AD是∠BAC的平分线.求证:AD=AC-AB.
参考答案
2020-2021学年北师大版八年级数学下册第一章1.3.2
线段的垂直平分线(二)
同步练习题
A组(基础题)
一、填空题
1.如图,小明把一个含30°
角的直角三角形纸板沿较短边的垂直平分线翻折,则∠BOC的度数是60°.
2.如图,A,B,C三个居民小区的位置成三角形,现决定在三个小区之间修建一个休闲广场,使广场到三个小区的距离相等,则广场应建在三边垂直平分线的交点处.
3.以线段AB为底边,以AB为高作等腰三角形ABC,则∠CAB=45°.
4.如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB的长度为7,则△ABC的周长为17.
二、选择题
5.如图,
AC=AD,
BC=BD,则有(A)
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相垂直平分
D.CD平分∠ACB
6.为了丰富学生的课余生活,某校举行联欢晚会,在联欢晚会上,有A,B,C三名同学站在一个三角形三个顶点的位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,凳子应放在△ABC的(D)
A.三边中线的交点处
B.三条角平分线的交点处
C.三边高的交点处
D.三边垂直平分线的交点处
7.过直线l外一点P作l的垂线,先在直线l上取两点A,B,使PA=PB,再作(D)
A.线段AB的垂线
B.∠PAB的平分线
C.∠PBA的平分线
D.∠APB的平分线
8.如图,点E,F,G,Q,H在一条直线上,且EF=GH,我们知道按如图所作的直线l为线段FG的垂直平分线.下列说法正确的是(A)
A.l是线段EH的垂直平分线
B.l是线段EQ的垂直平分线
C.l是线段FH的垂直平分线
D.EH是l的垂直平分线
三、解答题
9.(1)如图,已知AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F.求证:AD垂直平分EF.
证明:∵AD是△ABC的角平分线,
DE⊥AB,DF⊥AC,
∴DE=DF.
∴Rt△AED≌Rt△AFD.∴AE=AF.
∵AD是等腰△AEF的顶角平分线,
∴AD垂直平分EF.
(2)如图,在墙角点O处有一个老鼠洞,小猫在点A处发现老鼠从点B处往洞口逃窜,小猫想:这一次不会再让“你”逃掉.若小猫和老鼠的速度相同,你能确定小猫抓住老鼠的位置吗?
解:如图,连接AB,作线段AB的垂直平分线,交OB于点P,则小猫在点P处抓住老鼠.
10.如图,在△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E.求证:AD是CE的垂直平分线.
证明:∵∠ACB=90°,AD平分∠BAC,DE⊥AB,
∴DE=DC.
∴点D在线段CE的垂直平分线上.
∵∠EAD=∠CAD,∠AED=∠ACD=90°,DE=DC,
∴△AED≌△ACD(AAS).∴AE=AC.
∴点A在线段CE的垂直平分线上.
∴直线AD是CE的垂直平分线.
B组(中档题)
四、填空题
11.如图,分别以线段BD的端点B,D为圆心,相同的长度为半径画弧,两弧相交于A,C两点,连接AB,AD,CB,CD.若AB=2,BD=2,则四边形ABCD的面积为2.
12.在△ABC中,DF是AB的垂直平分线,交BC于点D,EG是AC的垂直平分线,交BC于点E.若∠DAE=30°,则∠BAC等于75°或105°.
13.(2019·哈尔滨)如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,
E为AD边上一点,连接BD,CE,CE与BD交于点F,且CE∥AB.若AB=8,CE=6,则BC的长为2.
五、解答题
14.如图所示,正方形ABCD的边长为1,G为CD边上的一个动点(点G与C,D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.
(1)求证:①△BCG≌△DCE;②BH⊥DE;
(2)试问当点G运动到什么位置时,BH垂直平分DE?请说明理由.
解:(1)证明:在正方形ABCD中,∠BCG=90°,BC=CD,
在正方形GCEF中,∠DCE=90°,CG=CE,
在△BCG和△DCE中,
∴△BCG≌△DCE(SAS).
∴∠1=∠2.
∵∠2+∠DEC=90°,
∴∠1+∠DEC=90°.
∴∠BHD=90°.
∴BH⊥DE.
(2)当GC=-1时,BH垂直平分DE.理由如下:
连接EG.
∵BH垂直平分DE.
∴EG=DG.
设CG=x,则CE=CG=x.
∵∠DCE=90°,
∴EG=x,DG=x.
∵DG+CG=CD,
∴x+x=1,解得x=-1.
∴当GC=-1时,BH垂直平分DE.
C组(综合题)
15.如图,已知在△ABC中,∠BAC∶∠ABC∶∠ACB=4∶2∶1,AD是∠BAC的平分线.求证:AD=AC-AB.
证明:在AC上截取AE=AB,连接DE,设∠C=x.
∵∠BAC∶∠ABC∶∠ACB=4∶2∶1,
∴∠BAC=4x,∠B=2x.
∵AD是∠BAC的平分线,∴∠BAD=∠DAE=2x.
在△ABD和△AED中,
∴△ABD≌△AED(SAS).∴∠B=∠AED=2x.
∴∠AED=∠DAE.∴DA=DE.
∵∠AED=∠EDC+∠C,∠C=x,
∴∠EDC=2x-x=x,即∠EDC=∠C,
∴ED=EC.∴DA=EC.
∴AC=AE+EC=AB+AD,即AD=AC-AB.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
