2020-2021学年苏科版七年级下册9.2 单项式乘多项式 提优训练(word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版七年级下册9.2 单项式乘多项式 提优训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 454.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-14 11:25:21 | ||
图片预览



文档简介
9.2 单项式乘多项式 提优训练
一、单选题
1.(2020·重庆市松树桥中学校七年级月考)计算的结果是( )
A. B. C. D.
2.(2019·南阳市第三中学)等于( )
A. B.
C. D.
3.(2021·山东济宁市·八年级期末)在一次数学课上,学习了单项式乘多项式,小明回家后,拿出课堂笔记本复习,发现这样一道题:﹣3x(﹣2x2+3x﹣1)=6x3﹣9x2+□,“□”的地方被墨水弄污了,你认为“□”内应填写( )
A.1 B.﹣1 C.3x D.﹣3x
4.(2020·保定市乐凯中学七年级期末)某同学在计算﹣3x2乘一个多项式时错误的计算成了加法,得到的答案是x2﹣x+1,由此可以推断该多项式是( )
A.4x2﹣x+1 B.x2﹣x+1 C.﹣2x2﹣x+1 D.无法确定
5.(2020·全国七年级课时练习) ,括号内应填的多项式为( )
A. B. C. D.
6.(2020·全国八年级课时练习)下列计算正确的是( )
A. B.
C. D.
7.(2020·浙江杭州市·七年级其他模拟)已知,则代数式的值为( )
A.2 B.1 C.0 D.-1
8.(2021·全国八年级)若,,则的值为(? ? ? ? )
A. B. C. D.
9.(2020·浙江杭州市·七年级其他模拟)已知,则的值为( )
A.2 B.6 C.10 D.14
10.(2020·江苏镇江市·七年级月考)若,则等于( )
A.2020 B.2019 C.2018 D.-2020
二、填空题
11.(2020·广西贺州市·七年级期中)计算:___________________________________________.
12.(2020·全国八年级课时练习)若的展开式中只含有项,则m的值为________.
13.(2020·南通市东方中学)已知单项式M,N满足,则等于_____________.
14.(2019·江西南昌二中八年级期中)已知,,,求:__________.
15.(2021·全国八年级)已知,那么的值是________.
16.(2020·浙江七年级月考)若a2﹣3a﹣1=0,则a(a﹣3)=_____________.
17.(2016·浙江杭州市·七年级期中)已知,则=__________.
18.(2020·重庆八中七年级课时练习)若一个多项式除以得到的商为,余式为,则这个多项式为______.
19.(2019·浙江杭州市·九年级)____.
20.(2020·湖北恩施土家族苗族自治州·八年级期末)若x=2019567891×2019567861,y=2019567881×2019567871,则x__y(填>,<或=).
三、解答题
21.(2021·广西钦州市·八年级期末)计算:
(1);
(2);
(3).
22.(2020·陕西汉中市·七年级期末)计算:
(1)
(2)
(3)(2m4n3+16m3n-8m2n5)÷(-2m2n)·(-mn)3
23.(2019·东莞市新世纪英才学校七年级月考)已知x、y为有理数,现规定一种新运算,满足.
(1)求的值;
(2)求的值;
(3)探索与的关系,并用等式把它们表达出来.
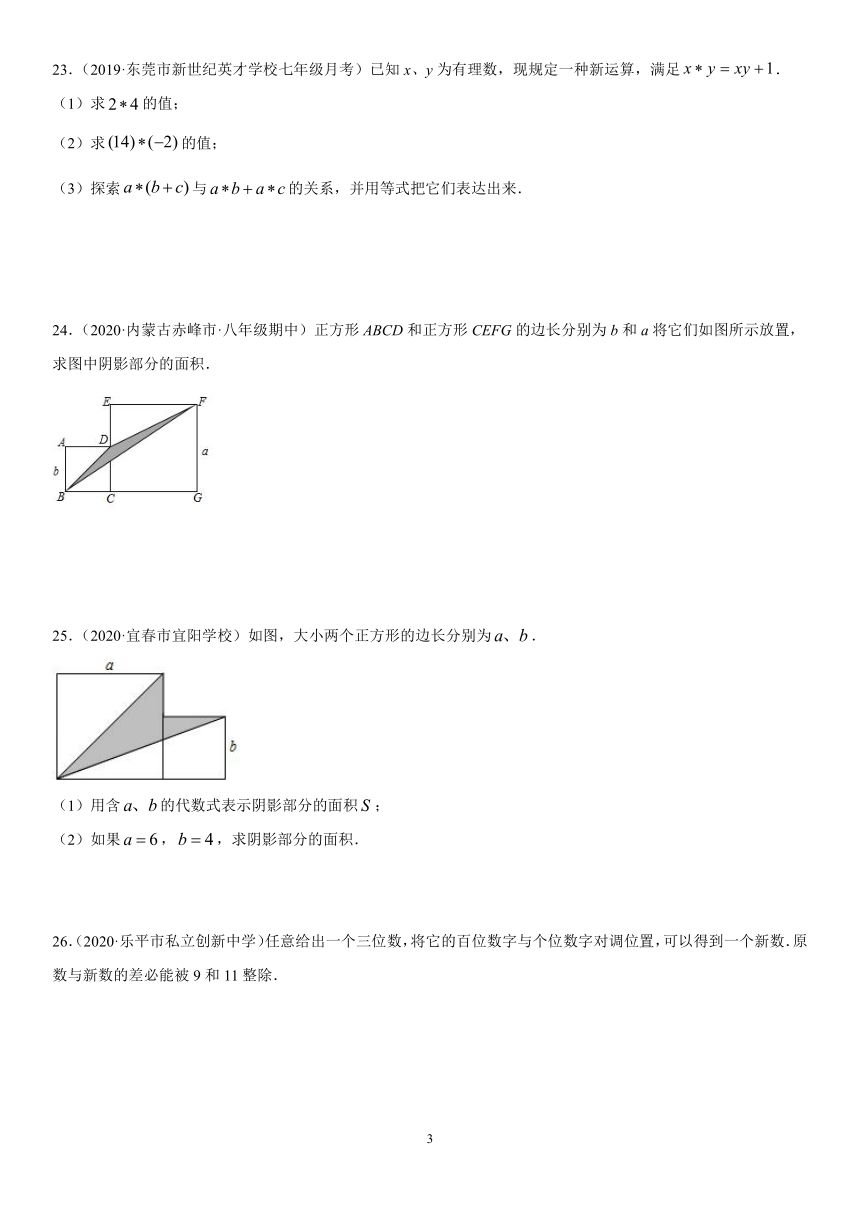
24.(2020·内蒙古赤峰市·八年级期中)正方形ABCD和正方形CEFG的边长分别为b和a将它们如图所示放置,求图中阴影部分的面积.
25.(2020·宜春市宜阳学校)如图,大小两个正方形的边长分别为.
(1)用含的代数式表示阴影部分的面积;
(2)如果,,求阴影部分的面积.
26.(2020·乐平市私立创新中学)任意给出一个三位数,将它的百位数字与个位数字对调位置,可以得到一个新数.原数与新数的差必能被9和11整除.
27.(2020·河南七年级期中)已知为有理数,现规定一种新运算,满足.
求的值;
求的值;
,探索与两个式子是否相等,说明理由.
28.(2020·江苏苏州市·七年级期中)阅读材料:求1+2+22+23+24+…+22013的值.
解:设S=1+2+22+23+24+…+22012+22013,将等式两边同时乘2,
得2S=2+22+23+24+25+…+22013+22014. 将下式减去上式,得2S﹣S=22014-1
即S=22014-1,
即1+2+22+23+24+…+22013=22014-1
仿照此法计算:(1)1+3+32+33+…+3100;(2)1++++…+,
参考答案
1.C 2.B 3.C 4.A 5.C 6.D 7.A 8.D 9.C 10.C
11.. 12.4 13.. 14.. 15. 16.1 17.2018 18. 19. 20.<
21.(1);(2);(3).
【详解】
(1)解:原式
(2)解:原式
(3)解:原式
22.(1);(2);(3).
【详解】
(1)=-8++9=
(2)=
(3)(2m4n3+16m3n-8m2n5)÷(-2m2n)·(-mn)3=(-m2n2-8m+4n4)·(-m3n3)=.
23.(1)9;(2)-27;(3)=+1.
【详解】
解:(1)∵,
∴;
(2),
∴;
(3))∵,
∴
∴=+1.
24.
【详解】
解:由题意得:
25.(1);(2)14.
【详解】
解:(1)大小两个正方形的边长分别为、,
阴影部分的面积为:
;
(2),,
.
所以阴影部分的面积是14.
26.证明见解析
【详解】
证明:设百位数字为x,十位数字为y,个位数字为z,
则原数为(100x+10y+z),新数为(100z+10y+x),
两数相减,得:
(100x+10y+z)﹣(100z+10y+x)
=100x﹣100z+z﹣x
=99x﹣99z
=99(x﹣y),
∵99能被9整除,也能被11整除,
∴原数与新数的差必能被9和11整除.
27.(1)8;(2)240;(3)不相等,理由见解析.
【详解】
(1);
(2);
(3)两个式子不相等,理由如下:
,
,
则,
,
,
,
因为,
所以,
所以与两个式子不相等.
28.(1);(2)
【详解】
(1)设S=1+3+32+33+…+3100,
两边乘以3得:3S=3+32+33+34+35+…+3100+3101,
将下式减去上式,得3S﹣S=3101﹣1
即S=,
即1+3+32+33+34+…+3100=
(2)设S=1++++…+,
两边乘以得:S=+++…+,
将下式减去上式得:-S=﹣1,
解得:S=2﹣,
即1++++…+=.
一、单选题
1.(2020·重庆市松树桥中学校七年级月考)计算的结果是( )
A. B. C. D.
2.(2019·南阳市第三中学)等于( )
A. B.
C. D.
3.(2021·山东济宁市·八年级期末)在一次数学课上,学习了单项式乘多项式,小明回家后,拿出课堂笔记本复习,发现这样一道题:﹣3x(﹣2x2+3x﹣1)=6x3﹣9x2+□,“□”的地方被墨水弄污了,你认为“□”内应填写( )
A.1 B.﹣1 C.3x D.﹣3x
4.(2020·保定市乐凯中学七年级期末)某同学在计算﹣3x2乘一个多项式时错误的计算成了加法,得到的答案是x2﹣x+1,由此可以推断该多项式是( )
A.4x2﹣x+1 B.x2﹣x+1 C.﹣2x2﹣x+1 D.无法确定
5.(2020·全国七年级课时练习) ,括号内应填的多项式为( )
A. B. C. D.
6.(2020·全国八年级课时练习)下列计算正确的是( )
A. B.
C. D.
7.(2020·浙江杭州市·七年级其他模拟)已知,则代数式的值为( )
A.2 B.1 C.0 D.-1
8.(2021·全国八年级)若,,则的值为(? ? ? ? )
A. B. C. D.
9.(2020·浙江杭州市·七年级其他模拟)已知,则的值为( )
A.2 B.6 C.10 D.14
10.(2020·江苏镇江市·七年级月考)若,则等于( )
A.2020 B.2019 C.2018 D.-2020
二、填空题
11.(2020·广西贺州市·七年级期中)计算:___________________________________________.
12.(2020·全国八年级课时练习)若的展开式中只含有项,则m的值为________.
13.(2020·南通市东方中学)已知单项式M,N满足,则等于_____________.
14.(2019·江西南昌二中八年级期中)已知,,,求:__________.
15.(2021·全国八年级)已知,那么的值是________.
16.(2020·浙江七年级月考)若a2﹣3a﹣1=0,则a(a﹣3)=_____________.
17.(2016·浙江杭州市·七年级期中)已知,则=__________.
18.(2020·重庆八中七年级课时练习)若一个多项式除以得到的商为,余式为,则这个多项式为______.
19.(2019·浙江杭州市·九年级)____.
20.(2020·湖北恩施土家族苗族自治州·八年级期末)若x=2019567891×2019567861,y=2019567881×2019567871,则x__y(填>,<或=).
三、解答题
21.(2021·广西钦州市·八年级期末)计算:
(1);
(2);
(3).
22.(2020·陕西汉中市·七年级期末)计算:
(1)
(2)
(3)(2m4n3+16m3n-8m2n5)÷(-2m2n)·(-mn)3
23.(2019·东莞市新世纪英才学校七年级月考)已知x、y为有理数,现规定一种新运算,满足.
(1)求的值;
(2)求的值;
(3)探索与的关系,并用等式把它们表达出来.
24.(2020·内蒙古赤峰市·八年级期中)正方形ABCD和正方形CEFG的边长分别为b和a将它们如图所示放置,求图中阴影部分的面积.
25.(2020·宜春市宜阳学校)如图,大小两个正方形的边长分别为.
(1)用含的代数式表示阴影部分的面积;
(2)如果,,求阴影部分的面积.
26.(2020·乐平市私立创新中学)任意给出一个三位数,将它的百位数字与个位数字对调位置,可以得到一个新数.原数与新数的差必能被9和11整除.
27.(2020·河南七年级期中)已知为有理数,现规定一种新运算,满足.
求的值;
求的值;
,探索与两个式子是否相等,说明理由.
28.(2020·江苏苏州市·七年级期中)阅读材料:求1+2+22+23+24+…+22013的值.
解:设S=1+2+22+23+24+…+22012+22013,将等式两边同时乘2,
得2S=2+22+23+24+25+…+22013+22014. 将下式减去上式,得2S﹣S=22014-1
即S=22014-1,
即1+2+22+23+24+…+22013=22014-1
仿照此法计算:(1)1+3+32+33+…+3100;(2)1++++…+,
参考答案
1.C 2.B 3.C 4.A 5.C 6.D 7.A 8.D 9.C 10.C
11.. 12.4 13.. 14.. 15. 16.1 17.2018 18. 19. 20.<
21.(1);(2);(3).
【详解】
(1)解:原式
(2)解:原式
(3)解:原式
22.(1);(2);(3).
【详解】
(1)=-8++9=
(2)=
(3)(2m4n3+16m3n-8m2n5)÷(-2m2n)·(-mn)3=(-m2n2-8m+4n4)·(-m3n3)=.
23.(1)9;(2)-27;(3)=+1.
【详解】
解:(1)∵,
∴;
(2),
∴;
(3))∵,
∴
∴=+1.
24.
【详解】
解:由题意得:
25.(1);(2)14.
【详解】
解:(1)大小两个正方形的边长分别为、,
阴影部分的面积为:
;
(2),,
.
所以阴影部分的面积是14.
26.证明见解析
【详解】
证明:设百位数字为x,十位数字为y,个位数字为z,
则原数为(100x+10y+z),新数为(100z+10y+x),
两数相减,得:
(100x+10y+z)﹣(100z+10y+x)
=100x﹣100z+z﹣x
=99x﹣99z
=99(x﹣y),
∵99能被9整除,也能被11整除,
∴原数与新数的差必能被9和11整除.
27.(1)8;(2)240;(3)不相等,理由见解析.
【详解】
(1);
(2);
(3)两个式子不相等,理由如下:
,
,
则,
,
,
,
因为,
所以,
所以与两个式子不相等.
28.(1);(2)
【详解】
(1)设S=1+3+32+33+…+3100,
两边乘以3得:3S=3+32+33+34+35+…+3100+3101,
将下式减去上式,得3S﹣S=3101﹣1
即S=,
即1+3+32+33+34+…+3100=
(2)设S=1++++…+,
两边乘以得:S=+++…+,
将下式减去上式得:-S=﹣1,
解得:S=2﹣,
即1++++…+=.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
