六年级下册数学课件-5.3 数与代数数的运算 西师大版 43张
文档属性
| 名称 | 六年级下册数学课件-5.3 数与代数数的运算 西师大版 43张 |  | |
| 格式 | zip | ||
| 文件大小 | 582.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 11:08:43 | ||
图片预览










文档简介
(共43张PPT)
1.
数与代数
数的运算
整理和复习
第一课时
一、提问导入,回顾旧知
(一)回顾复习方法
我们学过哪些运算?
加法、减法、乘法、除法,四种运算叫做四则运算。
出示:(提示)
1.
回忆加法、减法、乘法、除法的知识点
2.
熟悉这些知识的概念
3.
抓住知识点间的关系
4.
整理知识
要求:请根据提示,试着整理这一部分知识。
计算法则可以举例子来说明。
1.举例说明每种运算的意义:
加法的意义——把两个(或几个)数合并成一个数
的运算。
(二)汇报交流
二、整理复习旧识
举例说明每种运算的意义:
减法的意义——已知两个数的和与其中的一个加数,
求另一个加数是多少。
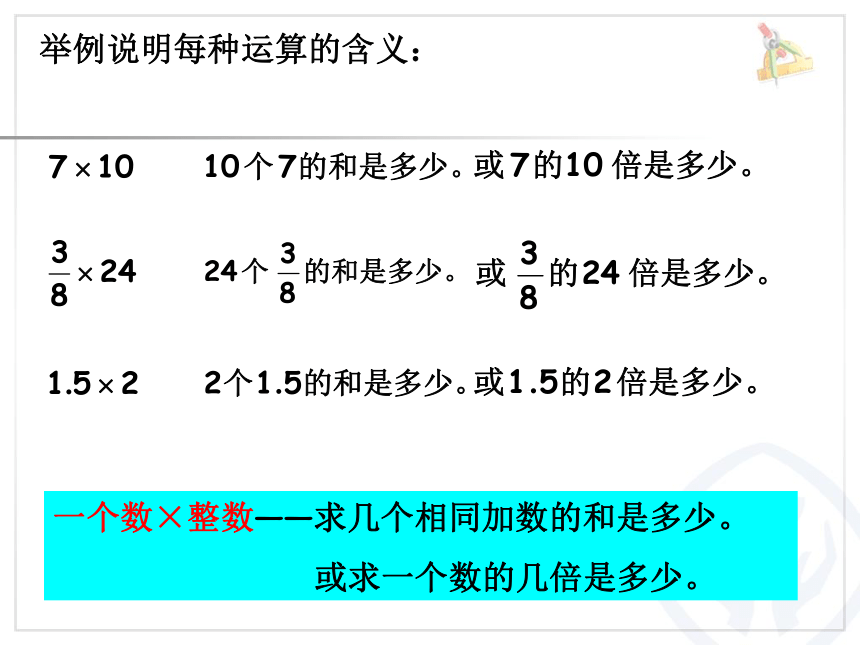
举例说明每种运算的含义:
一个数×整数——求几个相同加数的和是多少。
或求一个数的几倍是多少。
举例说明每种运算的意义:
一个数×小于1的小数——求一个数的十分之几、百分
之几、千分之几……是多少。
举例说明每种运算的意义:
一个数×大于1的小数——求一个数的几倍是多少。
举例说明每种运算的意义:
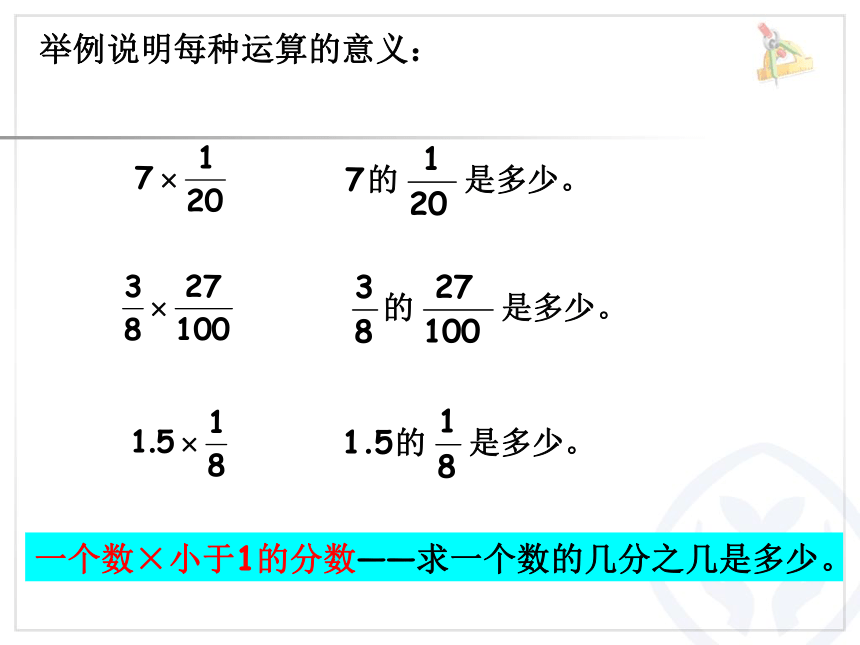
一个数×小于1的分数——求一个数的几分之几是多少。
举例说明每种运算的意义:
一个数×大于1的分数——求一个数的几倍是多少。
举例说明每种运算的意义:
除法的意义——已知两个因数的积和其中的一个因数,
求另一个因数是多少。
二、整理复习旧识
2.
运算的法则
请在小组内交流讨论,整数、小数、分数的运算法则有什么相同点?有什么不同点?可以举例说明。
整数
小数
分数
加减法
①相同数位对齐;
②从低位算起;
③加法中满几十就向前一位进几;减法中不够减时,就从前一位借,借几当几十。
①相同数位对齐(小数点对齐);
②从低位算起;
③按整数加减法的法则进行计算。
①同分母分数相加减,分母不变,分子相加减;
②异分母分数相加减,先通分再计算;
③结果能约分的要约分。
相同点:都是把相同计数单位的数相加减。
二、整理复习旧识
整数
小数
分数
乘法
①从个位乘起,依次用第二
个因数每位上的数字去乘第一个因数;
②用第二个因数哪一位上的数字去乘,得数的末位就和第二个因数的那一位对齐;
③再把几次乘得的数加起来
(整数末尾有0的乘法:可以先把0前面的数相乘,然后看各因数的末尾一共有几个0,就在乘得的数的末尾添写几个0。)
①按整数乘法的法则先求出积;
②看因数中共有几位小数,就从积的右边起数出几位点上小数点。数位不够0补足。
①分数乘分数,用分子相乘的积做分子,分母相乘的积做分母。
②有整数的把整数看作分母是1的假分数。
③有带分数的,通常先把带分数化成假分数。
④能约分的要先约分。
二、整理复习旧识
整数
小数
分数
除法
①从被除数的高位除起,除数是几位数,就先看被除数的前几位,如果不够除,就要多看一位。
②除到哪一位就要把商写到哪一位的上面。
③余数必须比除数小。
①如果除数是小数,先把它变成整数。除数的小数点向右移动几位,被除数的小数点也向右移动相同的位数(位数不够的补"0”),然后按照除数是整数的除法进行计算。
②商的小数点要和被除数的小数点对齐。
甲数除以乙数(0除外),等于甲数乘乙数的倒数。
二、整理复习旧识
小数乘除法和整数乘除法的相同点和不同点:
相同点:
小数乘法先按整数乘法计算法则计算,小数除法把除数转化成整数后,也按整数除法法则计算。
不同点:
小数乘、除法还要在计算结果上确定小数点的位置。
需要理解的计算规律:
一个不为0的数×大于1的数
→积大于原数
一个不为0的数×小于1的数
→积小于原数
一个不为0的数÷大于1的数
→商小于原数
一个不为0的数÷小于1的数
→商大于原数
二、整理复习旧识
乘大则大,乘小则小。
除大则小,除小则大。
二、整理复习旧识
3.
四则运算的关系
观察下列算式,说说四则运算之间的关系。
26+32=58
58-26=32
58-32=26
1.6+2.7=4.3
4.3-1.6=2.7
4.3-2.7=1.6
加数+加数=和
和-一个加数=另一个加数
被减数-减数=差
被减数-差=减数
减数+差=被减数
二、整理复习旧识
3.
四则运算的关系
观察下列算式,说说四则运算之间的关系。
125×8=1000
1000÷125=8
1000÷8=125
2.5×4=10
10÷2.5=4
10÷4=2.5
因数×因数=积
积÷一个因数=另一个因数
被除数÷除数=商
被除数÷商=除数
商×除数=被除数
加、减、乘、除法各部分之间的关系:
被除数÷除数=商……余数
(被除数-余数)÷商=除数
(被除数-余数)÷除数=商
商×除数+余数=被除数
54÷5=10……4
10×5+4=54
(54-4)÷10=5
(54-4)÷5=10
加法可用减法验算,减法可用加法或减法验算。
乘法可用除法验算,除法可用乘法或除法验算。
加法
减法
乘法
除法
逆运算
简便运算
逆运算
四则运算之间的关系:
四则运算中要注意的特殊情况:
a+0=
a-0=
a-a=
a×0=
a×1=
a÷1=
0÷a=
a÷a=
1÷a=
(以下算式中的a
作除数时不等于0)
2a
a
0
a
a
0
0
1
1
a
a+a
=
加法:
减法:
乘法:
除法:
a
a2
a×a
=
二、整理复习旧识
请在小组内讨论,四则混合运算的顺序是什么?可以举例说说。
如果是同一级运算,一般按从左往右依次进行计算。
如果既有加减、又有乘除法,先算乘除法、再算加减。
如果有括号,先算括号里面的。
巩固练习
认真观察每一道计算题,先想想是什么运算。再想想运算方法是什么。
最后想想需要注意些什么。
73.05-3.96
27.5×1.4
3.12÷15+4.71
12.5×28-193
-
+
5
4
3
2
6
1
×
÷5
4
3
3
1
×
÷
+
6
5
9
4
3
10
3
7
第二课时
运算定律和运算性质:
名称
举例
用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
减法的性质1
减法的性质2
除法的性质1
除法的性质2
5×6=6×5
37×25×4=37×(
25×4)
24×36+76×36=(24+76)×36
8+5=5+8
37+46+23=46+(37+23)
72-9-21=72-(9+21)
75-39-25=75-25-39
210÷6÷5=210÷
(6×5)
210÷15÷7=210÷7÷15
a×b=b×a
(a×b)×c=a×(
b×c)
ac±bc=(a±b)×c
a+b=b+a
(a+b)+c=a+(b+c)
a-b-c=a-(b+c)
a-b-c=a-c-b
a÷b÷c=a÷(b×c)
a÷b÷c=a÷c÷b
我们学过哪些运算定律?
一些混合运算也可以用简便方法计算:
121-37+79=121+79-37
a-b+c=a+c-b
121+37-21=121-21+37
a+b-c=a-c+b
60÷25×5=60×5÷25
210×9÷3=210÷3×9
a÷b×c=a×c÷b
a×b÷c=a÷c×b
加减混合,可以任意交换第一个数后面的数的运算次序。
乘除混合,可以任意交换第一个数后面的数的运算次序。
189-(89-47)=189-89+47
a-(b-c)=a-b+c
65+(35-27)=65+35-27
a+(b-c)=a+b-c
括号前面是减号,打开括号要变号,加变减,减变加。
括号前面是加号,打开括号不变号。
90÷(30÷2)=90÷30×2
a÷(b÷c)=a÷b×c
15×(20÷10)=15×20÷10
a×(b÷c)=a×b÷c
括号前面是除号,打开括号要变号,除变乘,乘变除。
括号前面是乘号,打开括号不变号。
64÷(16×2)=90÷30÷2
a÷(b×c)=a÷b÷c
34-(14+17)=34-14-17
a-(b+c)=a-b-c
65+(35+27)=65+35+27
a+(b+c)=a+b+c
25×(4×27)=25×4×27
a×(b×c)=a×b×c
a÷(b+c)=a÷b+a÷c
(a+b)÷c=a÷c+b÷c
下面两个运算性质是否正确?
×
√
练
习
1、287+299
=287+300-1
=587-1
=586
2、858-399
=858-400+1
=458+1
=459
3、125×32×25
=125×(8×4)×25
=(125×8)×(4×25)
=1000×100
=100000
4、(1.25+1.25+1.25+1.25)×25×8
=1.25×4×25×8
=(1.25×8)×(25×4)
=10×100
=1000
5、8.8×125
=(8+0.8)×125
=8×125+0.8×125
=1000+100
=1100
6、8.8×125
=8×1.1×125
=8×125×1.1
=1000×1.1
=1100
你觉得两种做法,哪一种更好?
9、3.46×6.8+65.4×0.68
=3.46×6.8+6.54×6.8
=(3.46+6.54)×6.8
=10×6.8
=68
(1)
45与39的和除以62与58的差,商是多少?
和
÷
差
45
+
39
÷
62—58
(
)
(
)
文字题:
(2)用84与40的差去除160与720的和,商是多少?
和
÷
差
160+720
÷
84-40
(
)
(
)
“除以”与“除”的区别:
“除以”是正叙,前面的是被除数,后面的是除数。
“除”是倒叙,前面的是除数,后面的是被除数。
(3)156除以52的商,再乘8与24的和,积是多少?
商
×
和
156÷52
×
8+24
(
)
(4)7除以0.14的商减去15与21的和,差是多少?
商
-
和
7÷0.14
-
15+21
(
)
解:设这个数为x。
(6)一个数与8的和的2倍是36,这个数是多少?
解:设这个数为x。
(x+8)×2=36
(7)一个数的4倍减去5个3.2的和,差是14,求这个数。
解:设这个数为x。
4x-3.2×5=14
(8)一个数的4倍比0.4除15.6的商少7,求这个数。
解:设这个数为x。
15.6÷0.4
-
4x=7
(9)55.8与4.8的差除以0.51的商比162少多少?
162
-
55.8
-
4.8
÷
0.51
(
)
解答文字题的规律:
规律1:如果问题中有“和是多少?”、“差是多少?”、“积是多少?”或“商是多少?”,那么题目里一定有“加”、“减”、“乘”、“除以”、“除”等相对应的词语。
规律2:题目里有“和”、“差”、“积”、“商”的,要先算出来。
规律3:题目要求“求这个数”或“这个数是多少?”的文字题,一般要用方程解答比较简便。
规律4:注意“……比……多(少)”这样的关键字,这样的问题涉及较大量、较小量和相差量。
规律5:括号是为了改变运算顺序,必要时才能使用,规律是先用小括号,再用中括号。
1.
数与代数
数的运算
整理和复习
第一课时
一、提问导入,回顾旧知
(一)回顾复习方法
我们学过哪些运算?
加法、减法、乘法、除法,四种运算叫做四则运算。
出示:(提示)
1.
回忆加法、减法、乘法、除法的知识点
2.
熟悉这些知识的概念
3.
抓住知识点间的关系
4.
整理知识
要求:请根据提示,试着整理这一部分知识。
计算法则可以举例子来说明。
1.举例说明每种运算的意义:
加法的意义——把两个(或几个)数合并成一个数
的运算。
(二)汇报交流
二、整理复习旧识
举例说明每种运算的意义:
减法的意义——已知两个数的和与其中的一个加数,
求另一个加数是多少。
举例说明每种运算的含义:
一个数×整数——求几个相同加数的和是多少。
或求一个数的几倍是多少。
举例说明每种运算的意义:
一个数×小于1的小数——求一个数的十分之几、百分
之几、千分之几……是多少。
举例说明每种运算的意义:
一个数×大于1的小数——求一个数的几倍是多少。
举例说明每种运算的意义:
一个数×小于1的分数——求一个数的几分之几是多少。
举例说明每种运算的意义:
一个数×大于1的分数——求一个数的几倍是多少。
举例说明每种运算的意义:
除法的意义——已知两个因数的积和其中的一个因数,
求另一个因数是多少。
二、整理复习旧识
2.
运算的法则
请在小组内交流讨论,整数、小数、分数的运算法则有什么相同点?有什么不同点?可以举例说明。
整数
小数
分数
加减法
①相同数位对齐;
②从低位算起;
③加法中满几十就向前一位进几;减法中不够减时,就从前一位借,借几当几十。
①相同数位对齐(小数点对齐);
②从低位算起;
③按整数加减法的法则进行计算。
①同分母分数相加减,分母不变,分子相加减;
②异分母分数相加减,先通分再计算;
③结果能约分的要约分。
相同点:都是把相同计数单位的数相加减。
二、整理复习旧识
整数
小数
分数
乘法
①从个位乘起,依次用第二
个因数每位上的数字去乘第一个因数;
②用第二个因数哪一位上的数字去乘,得数的末位就和第二个因数的那一位对齐;
③再把几次乘得的数加起来
(整数末尾有0的乘法:可以先把0前面的数相乘,然后看各因数的末尾一共有几个0,就在乘得的数的末尾添写几个0。)
①按整数乘法的法则先求出积;
②看因数中共有几位小数,就从积的右边起数出几位点上小数点。数位不够0补足。
①分数乘分数,用分子相乘的积做分子,分母相乘的积做分母。
②有整数的把整数看作分母是1的假分数。
③有带分数的,通常先把带分数化成假分数。
④能约分的要先约分。
二、整理复习旧识
整数
小数
分数
除法
①从被除数的高位除起,除数是几位数,就先看被除数的前几位,如果不够除,就要多看一位。
②除到哪一位就要把商写到哪一位的上面。
③余数必须比除数小。
①如果除数是小数,先把它变成整数。除数的小数点向右移动几位,被除数的小数点也向右移动相同的位数(位数不够的补"0”),然后按照除数是整数的除法进行计算。
②商的小数点要和被除数的小数点对齐。
甲数除以乙数(0除外),等于甲数乘乙数的倒数。
二、整理复习旧识
小数乘除法和整数乘除法的相同点和不同点:
相同点:
小数乘法先按整数乘法计算法则计算,小数除法把除数转化成整数后,也按整数除法法则计算。
不同点:
小数乘、除法还要在计算结果上确定小数点的位置。
需要理解的计算规律:
一个不为0的数×大于1的数
→积大于原数
一个不为0的数×小于1的数
→积小于原数
一个不为0的数÷大于1的数
→商小于原数
一个不为0的数÷小于1的数
→商大于原数
二、整理复习旧识
乘大则大,乘小则小。
除大则小,除小则大。
二、整理复习旧识
3.
四则运算的关系
观察下列算式,说说四则运算之间的关系。
26+32=58
58-26=32
58-32=26
1.6+2.7=4.3
4.3-1.6=2.7
4.3-2.7=1.6
加数+加数=和
和-一个加数=另一个加数
被减数-减数=差
被减数-差=减数
减数+差=被减数
二、整理复习旧识
3.
四则运算的关系
观察下列算式,说说四则运算之间的关系。
125×8=1000
1000÷125=8
1000÷8=125
2.5×4=10
10÷2.5=4
10÷4=2.5
因数×因数=积
积÷一个因数=另一个因数
被除数÷除数=商
被除数÷商=除数
商×除数=被除数
加、减、乘、除法各部分之间的关系:
被除数÷除数=商……余数
(被除数-余数)÷商=除数
(被除数-余数)÷除数=商
商×除数+余数=被除数
54÷5=10……4
10×5+4=54
(54-4)÷10=5
(54-4)÷5=10
加法可用减法验算,减法可用加法或减法验算。
乘法可用除法验算,除法可用乘法或除法验算。
加法
减法
乘法
除法
逆运算
简便运算
逆运算
四则运算之间的关系:
四则运算中要注意的特殊情况:
a+0=
a-0=
a-a=
a×0=
a×1=
a÷1=
0÷a=
a÷a=
1÷a=
(以下算式中的a
作除数时不等于0)
2a
a
0
a
a
0
0
1
1
a
a+a
=
加法:
减法:
乘法:
除法:
a
a2
a×a
=
二、整理复习旧识
请在小组内讨论,四则混合运算的顺序是什么?可以举例说说。
如果是同一级运算,一般按从左往右依次进行计算。
如果既有加减、又有乘除法,先算乘除法、再算加减。
如果有括号,先算括号里面的。
巩固练习
认真观察每一道计算题,先想想是什么运算。再想想运算方法是什么。
最后想想需要注意些什么。
73.05-3.96
27.5×1.4
3.12÷15+4.71
12.5×28-193
-
+
5
4
3
2
6
1
×
÷5
4
3
3
1
×
÷
+
6
5
9
4
3
10
3
7
第二课时
运算定律和运算性质:
名称
举例
用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
减法的性质1
减法的性质2
除法的性质1
除法的性质2
5×6=6×5
37×25×4=37×(
25×4)
24×36+76×36=(24+76)×36
8+5=5+8
37+46+23=46+(37+23)
72-9-21=72-(9+21)
75-39-25=75-25-39
210÷6÷5=210÷
(6×5)
210÷15÷7=210÷7÷15
a×b=b×a
(a×b)×c=a×(
b×c)
ac±bc=(a±b)×c
a+b=b+a
(a+b)+c=a+(b+c)
a-b-c=a-(b+c)
a-b-c=a-c-b
a÷b÷c=a÷(b×c)
a÷b÷c=a÷c÷b
我们学过哪些运算定律?
一些混合运算也可以用简便方法计算:
121-37+79=121+79-37
a-b+c=a+c-b
121+37-21=121-21+37
a+b-c=a-c+b
60÷25×5=60×5÷25
210×9÷3=210÷3×9
a÷b×c=a×c÷b
a×b÷c=a÷c×b
加减混合,可以任意交换第一个数后面的数的运算次序。
乘除混合,可以任意交换第一个数后面的数的运算次序。
189-(89-47)=189-89+47
a-(b-c)=a-b+c
65+(35-27)=65+35-27
a+(b-c)=a+b-c
括号前面是减号,打开括号要变号,加变减,减变加。
括号前面是加号,打开括号不变号。
90÷(30÷2)=90÷30×2
a÷(b÷c)=a÷b×c
15×(20÷10)=15×20÷10
a×(b÷c)=a×b÷c
括号前面是除号,打开括号要变号,除变乘,乘变除。
括号前面是乘号,打开括号不变号。
64÷(16×2)=90÷30÷2
a÷(b×c)=a÷b÷c
34-(14+17)=34-14-17
a-(b+c)=a-b-c
65+(35+27)=65+35+27
a+(b+c)=a+b+c
25×(4×27)=25×4×27
a×(b×c)=a×b×c
a÷(b+c)=a÷b+a÷c
(a+b)÷c=a÷c+b÷c
下面两个运算性质是否正确?
×
√
练
习
1、287+299
=287+300-1
=587-1
=586
2、858-399
=858-400+1
=458+1
=459
3、125×32×25
=125×(8×4)×25
=(125×8)×(4×25)
=1000×100
=100000
4、(1.25+1.25+1.25+1.25)×25×8
=1.25×4×25×8
=(1.25×8)×(25×4)
=10×100
=1000
5、8.8×125
=(8+0.8)×125
=8×125+0.8×125
=1000+100
=1100
6、8.8×125
=8×1.1×125
=8×125×1.1
=1000×1.1
=1100
你觉得两种做法,哪一种更好?
9、3.46×6.8+65.4×0.68
=3.46×6.8+6.54×6.8
=(3.46+6.54)×6.8
=10×6.8
=68
(1)
45与39的和除以62与58的差,商是多少?
和
÷
差
45
+
39
÷
62—58
(
)
(
)
文字题:
(2)用84与40的差去除160与720的和,商是多少?
和
÷
差
160+720
÷
84-40
(
)
(
)
“除以”与“除”的区别:
“除以”是正叙,前面的是被除数,后面的是除数。
“除”是倒叙,前面的是除数,后面的是被除数。
(3)156除以52的商,再乘8与24的和,积是多少?
商
×
和
156÷52
×
8+24
(
)
(4)7除以0.14的商减去15与21的和,差是多少?
商
-
和
7÷0.14
-
15+21
(
)
解:设这个数为x。
(6)一个数与8的和的2倍是36,这个数是多少?
解:设这个数为x。
(x+8)×2=36
(7)一个数的4倍减去5个3.2的和,差是14,求这个数。
解:设这个数为x。
4x-3.2×5=14
(8)一个数的4倍比0.4除15.6的商少7,求这个数。
解:设这个数为x。
15.6÷0.4
-
4x=7
(9)55.8与4.8的差除以0.51的商比162少多少?
162
-
55.8
-
4.8
÷
0.51
(
)
解答文字题的规律:
规律1:如果问题中有“和是多少?”、“差是多少?”、“积是多少?”或“商是多少?”,那么题目里一定有“加”、“减”、“乘”、“除以”、“除”等相对应的词语。
规律2:题目里有“和”、“差”、“积”、“商”的,要先算出来。
规律3:题目要求“求这个数”或“这个数是多少?”的文字题,一般要用方程解答比较简便。
规律4:注意“……比……多(少)”这样的关键字,这样的问题涉及较大量、较小量和相差量。
规律5:括号是为了改变运算顺序,必要时才能使用,规律是先用小括号,再用中括号。
