2020-2021学年九年级数学人教版下册 课件: 28.2.1 解直角三角形(21张)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册 课件: 28.2.1 解直角三角形(21张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 494.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-14 12:33:53 | ||
图片预览








文档简介
第二十八章 锐角三角函数
28.2 解直角三角形及其应用
28.2.1 解直角三角形
目
录
CONTENTS
1 学习目标
2 新课导入
3 新课讲解
4 课堂小结
5 当堂小练
6 拓展与延伸
1. 了解并掌握解直角三角形的概念;
2. 理解直角三角形中的五个元素之间的联系. (重点)
3. 学会解直角三角形. (难点)
学习目标
新课导入
复习引入
A
C
B
c
b
a
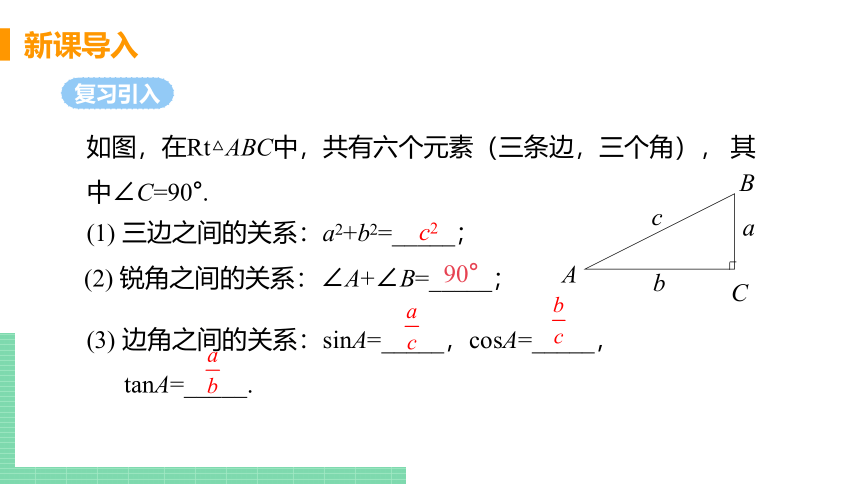
(1) 三边之间的关系:a2+b2=_____;
(2) 锐角之间的关系:∠A+∠B=_____;
(3) 边角之间的关系:sinA=_____,cosA=_____,
tanA=_____.
如图,在Rt△ABC中,共有六个元素(三条边,三个角), 其中∠C=90°.
c2
90°
新课讲解
知识点1 已知两边解直角三角形
合作探究
在图中的Rt△ABC中,
(1) 根据∠A=75°,斜边AB=6,你能求出这个直角三角形的其他元素吗?
A
B
C
6
75°
新课讲解
(2) 根据AC=2.4,斜边AB=6,你能求出这个直角三角形的其他元素吗?
A
B
C
6
2.4
新课讲解
归纳
在直角三角形中,除直角外有5个元素(即3条边、2个锐角),只要知道其中的2个元素(至少有1个是边),就可以求出其余的3个未知元素.
由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
新课讲解
典例精析
A
B
C
解:
例1 如图,在Rt△ABC中,∠C = 90°,AC = , ,解这个直角三角形.
∴∠A=60°
∠B=90°-60°=30°
新课讲解
练一练
在Rt△ABC中,∠C=90°,a = 30,b = 20,根据条件解直角三角形.
解:根据勾股定理
A
B
C
b=20
a=30
c
新课讲解
知识点2 已知一边及一锐角解直角三角形
例2 如图,在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形 (结果保留小数点后一位).
A
B
C
b=20
c
a
35°
解:
新课讲解
2. 如图,已知 AC = 4,求 AB 和 BC 的长.
提示:作CD⊥AB于点D,根据三角函数的定义,在Rt△ACD,Rt△CDB中,即可求出 CD,AD,BD 的长,从而求解.
新课讲解
2. 如图,已知 AC = 4,求 AB 和 BC 的长.
在Rt△CDB中,∵∠DCB=∠ACB-∠ACD=45°,
D
解:如图,作CD⊥AB于点D,
在Rt△ACD中,∵∠A=30°,∴∠ACD=90°-∠A=60°,
∴BD=CD=2.
新课讲解
知识点3 已知一锐角三角函数值解直角三角形
例3 如图,在Rt△ABC 中,∠C=90°,cosA = ,
BC = 5, 试求AB的长.
A
C
B
解:
设
新课讲解
A
C
B
∴ AB的长为
新课讲解
练一练
1. 在Rt△ABC中,∠C=90°,sinA = ,BC=6,则AB的长为 ( )
A.4 B.6 C.8 D.10
D
2. 如图,在菱形ABCD中,AE⊥BC于点E,EC=4,
sinB= ,则菱形的周长是 ( )
A.10 B.20
C.40 D.28
C
课堂小结
解直角三角形
依据
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素
勾股定理
两锐角互余
锐角的三角函数
当堂小练
C
2. 如图,在Rt△ABC中,∠C=90°,∠B=30°, AB=8,则BC的长是( )
D
A
C
B
?
1. 在Rt△ABC中,∠C=90°,a,b,c分别是∠A, ∠B,∠C的对边,则下列各式正确的是 ( )
A. b=a·tanA B. b=c·sinA
C. b=c·cosA D. a=c·cosA
当堂小练
3. 在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC = (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
4. 如图,已知Rt△ABC中,斜边BC上的高AD=3,cosB
= ,则 AC 的长为 .
24
3.75
当堂小练
5. 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,
解这个直角三角形.
解:
∵ AD平分∠BAC,
D
A
B
C
6
拓展与延伸
解:过点 A作 AD⊥BC于点D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD=sinC · AC= 2sin45°= .
在△ABD中,∠B=30°,
∴BD=
∴BC=CD+BD=
6. 如图,在△ABC中,∠B=30°,∠C=45°,AC=2,求BC的长.
D
A
B
C
THANKS
28.2 解直角三角形及其应用
28.2.1 解直角三角形
目
录
CONTENTS
1 学习目标
2 新课导入
3 新课讲解
4 课堂小结
5 当堂小练
6 拓展与延伸
1. 了解并掌握解直角三角形的概念;
2. 理解直角三角形中的五个元素之间的联系. (重点)
3. 学会解直角三角形. (难点)
学习目标
新课导入
复习引入
A
C
B
c
b
a
(1) 三边之间的关系:a2+b2=_____;
(2) 锐角之间的关系:∠A+∠B=_____;
(3) 边角之间的关系:sinA=_____,cosA=_____,
tanA=_____.
如图,在Rt△ABC中,共有六个元素(三条边,三个角), 其中∠C=90°.
c2
90°
新课讲解
知识点1 已知两边解直角三角形
合作探究
在图中的Rt△ABC中,
(1) 根据∠A=75°,斜边AB=6,你能求出这个直角三角形的其他元素吗?
A
B
C
6
75°
新课讲解
(2) 根据AC=2.4,斜边AB=6,你能求出这个直角三角形的其他元素吗?
A
B
C
6
2.4
新课讲解
归纳
在直角三角形中,除直角外有5个元素(即3条边、2个锐角),只要知道其中的2个元素(至少有1个是边),就可以求出其余的3个未知元素.
由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.
新课讲解
典例精析
A
B
C
解:
例1 如图,在Rt△ABC中,∠C = 90°,AC = , ,解这个直角三角形.
∴∠A=60°
∠B=90°-60°=30°
新课讲解
练一练
在Rt△ABC中,∠C=90°,a = 30,b = 20,根据条件解直角三角形.
解:根据勾股定理
A
B
C
b=20
a=30
c
新课讲解
知识点2 已知一边及一锐角解直角三角形
例2 如图,在Rt△ABC中,∠C=90°,∠B=35°,b=20,解这个直角三角形 (结果保留小数点后一位).
A
B
C
b=20
c
a
35°
解:
新课讲解
2. 如图,已知 AC = 4,求 AB 和 BC 的长.
提示:作CD⊥AB于点D,根据三角函数的定义,在Rt△ACD,Rt△CDB中,即可求出 CD,AD,BD 的长,从而求解.
新课讲解
2. 如图,已知 AC = 4,求 AB 和 BC 的长.
在Rt△CDB中,∵∠DCB=∠ACB-∠ACD=45°,
D
解:如图,作CD⊥AB于点D,
在Rt△ACD中,∵∠A=30°,∴∠ACD=90°-∠A=60°,
∴BD=CD=2.
新课讲解
知识点3 已知一锐角三角函数值解直角三角形
例3 如图,在Rt△ABC 中,∠C=90°,cosA = ,
BC = 5, 试求AB的长.
A
C
B
解:
设
新课讲解
A
C
B
∴ AB的长为
新课讲解
练一练
1. 在Rt△ABC中,∠C=90°,sinA = ,BC=6,则AB的长为 ( )
A.4 B.6 C.8 D.10
D
2. 如图,在菱形ABCD中,AE⊥BC于点E,EC=4,
sinB= ,则菱形的周长是 ( )
A.10 B.20
C.40 D.28
C
课堂小结
解直角三角形
依据
解法:只要知道五个元素中的两个元素(至少有一个是边),就可以求出余下的三个未知元素
勾股定理
两锐角互余
锐角的三角函数
当堂小练
C
2. 如图,在Rt△ABC中,∠C=90°,∠B=30°, AB=8,则BC的长是( )
D
A
C
B
?
1. 在Rt△ABC中,∠C=90°,a,b,c分别是∠A, ∠B,∠C的对边,则下列各式正确的是 ( )
A. b=a·tanA B. b=c·sinA
C. b=c·cosA D. a=c·cosA
当堂小练
3. 在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC = (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
4. 如图,已知Rt△ABC中,斜边BC上的高AD=3,cosB
= ,则 AC 的长为 .
24
3.75
当堂小练
5. 如图,在Rt△ABC中,∠C=90°,AC=6, ∠BAC的平分线 ,
解这个直角三角形.
解:
∵ AD平分∠BAC,
D
A
B
C
6
拓展与延伸
解:过点 A作 AD⊥BC于点D.
在△ACD中,∠C=45°,AC=2,
∴CD=AD=sinC · AC= 2sin45°= .
在△ABD中,∠B=30°,
∴BD=
∴BC=CD+BD=
6. 如图,在△ABC中,∠B=30°,∠C=45°,AC=2,求BC的长.
D
A
B
C
THANKS
