2020-2021学年九年级数学人教版下册课件: 27.2.2 相似三角形的性质(27张)
文档属性
| 名称 | 2020-2021学年九年级数学人教版下册课件: 27.2.2 相似三角形的性质(27张) |  | |
| 格式 | pptx | ||
| 文件大小 | 491.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-14 12:46:10 | ||
图片预览








文档简介
第二十七章 相似
27.2 相似三角形
27.2.2 相似三角形的性质
目
录
CONTENTS
1 学习目标
2 新课导入
3 新课讲解
4 课堂小结
5 当堂小练
6 拓展与延伸
1. 理解并掌握相似三角形中对应线段的比等于相似比,并运用其解决问题. (重点、难点)
2. 理解相似三角形面积的比等于相似比的平方,并运用其解决问题. (重点)
学习目标
新课导入
情景导入
三角形除了三个角,三条边外,还有哪些要素?
高
中线
角平分线
周长
面积
如果两个三角形相似,那
么,对应的这些要素
有什么关系呢?
新课讲解
知识点1 相似三角形对应线段的比
合作探究
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
新课讲解
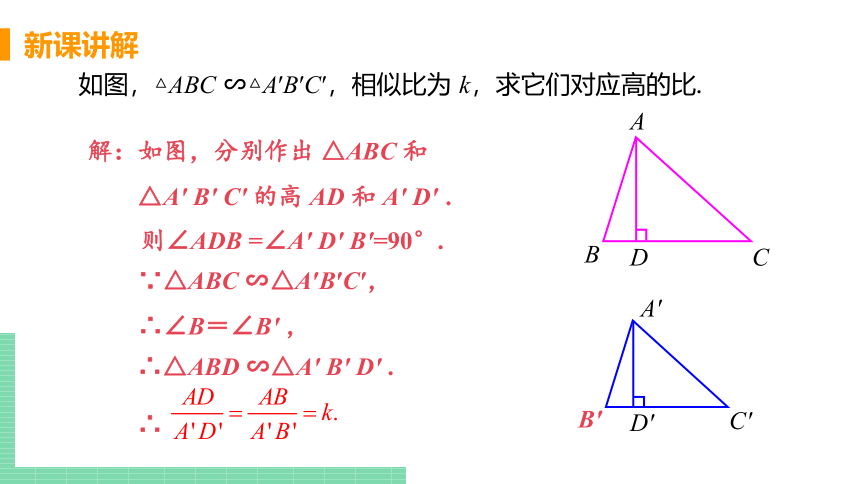
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
解:如图,分别作出 △ABC 和
△A' B' C' 的高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
∴
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应高的比.
新课讲解
试一试
仿照求高的比的过程,当△ABC ∽△A′B′C′,相似比为 k 时,求它们对应中线的比、对应角平分线的比.
新课讲解
结论
由此我们可以得到:
相似三角形对应高的比等于相似比.
类似地,可以证明:
相似三角形对应中线、角平分线的比也等于相似比.
一般地,我们有:
相似三角形对应线段的比等于相似比.
新课讲解
例
典例分析
解:∵ △ABC ∽△DEF,
D
E
F
H
已知 △ABC∽△DEF,BG、EH 分别是 △ABC和 △DEF 的角平分线,BC = 6 cm,EF = 4 cm,BG= 4.8 cm. 求 EH 的长.
∴
(相似三角形对应角平分线的比等于相似比),
∴ ,解得 EH = 3.2.
A
G
B
C
∴ EH 的长为 3.2 cm.
新课讲解
练一练
1. 如果两个相似三角形的对应高的比为 2 : 3,那么对 应角平分线的比是 ,对应边上的中线的比是 ______ .
2. 已知△ABC ∽ △A'B'C' ,相似比为3 : 4,若 BC 边上的高 AD=12 cm,则 B'C' 边上的高 A'D' =______ .
2 : 3
2 : 3
16 cm
新课讲解
想一想:
相似三角形的周长比也等于相似比吗?为什么?
新课讲解
如果 △ABC ∽△A'B'C',相似比为 k,那么
因此
AB=k A'B',BC=kB'C',CA=kC'A',
从而
结论
相似三角形周长的比等于相似比.
新课讲解
知识点2 相似三角形面积的比
合作探究
如图,△ABC ∽△A′B′C′,相似比为 k,它们的面积比是多少?
A
B
C
A'
B'
C'
新课讲解
由前面的结论,我们有
A
B
C
A'
B'
C'
D'
D
新课讲解
结论
相似三角形面积的比等于相似比的平方.
新课讲解
典例分析
1. 已知两个三角形相似,请完成下列表格:
相似比
2
k
……
周长比
……
面积比
10000
……
2
4
100
100
k
k2
新课讲解
练一练
2. 把一个三角形变成和它相似的三角形,
(1) 如果边长扩大为原来的 5 倍,那么面积扩大为 原来的______倍;
(2) 如果面积扩大为原来的 100 倍,那么边长扩大为原来的_____倍.
25
10
新课讲解
练一练
3. 两个相似三角形的一对对应边分别是 35 cm、14 cm,
(1) 它们的周长差为 60 cm,这两个三角形的周长分别________________;
(2) 它们的面积之和是 58 cm2,这两个三角形的面积分别是______________.
100 cm、40 cm
50 cm2、8 cm2
新课讲解
练一练
如图,D,E 分别是 AC,AB 上的点,已知△ABC 的面积为100 cm2,且 ,求四边形 BCDE 的面积.
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5,∴ 面积比为 9 : 25.
B
C
A
D
E
解:∵ ∠BAC = ∠DAE,且
又∵ △ABC 的面积为 100 cm2,
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为100-36 = 64 (cm2).
课堂小结
相似三角形性质的运用
相似三角形面积的比等于相似比的平方
相似三角形的性质
相似三角形对应线段的比等于相似比
当堂小练
1. 判断:
(1) 一个三角形的各边长扩大为原来的 5 倍,这个
三角形的周长也扩大为原来的 5 倍 ( )
(2) 一个四边形的各边长扩大为原来的 9 倍,这个
四边形的面积也扩大为原来的 9 倍 ( )
√
×
当堂小练
3. 连接三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积 比等于_____.
1 : 2
1 : 4
2. 在 △ABC 和 △DEF 中,AB=2 DE,AC=2 DF,∠A=∠D,AP,DQ 是中线,若 AP=2,则 DQ的值为 ( )
A.2 B.4 C.1 D.
C
当堂小练
4. 两个相似三角形对应的中线长分别是 6 cm 和 18 cm,若较大三角形的周长是 42 cm,面积是 12 cm2,则较小三角形的周长____cm,面积为____cm2.
14
当堂小练
5. △ABC 中,DE∥BC,EF∥AB,已知 △ADE 和
△EFC 的面积分别为 4 和 9,求 △ABC 的面积.
A
B
C
D
F
E
解:∵ DE∥BC,EF∥AB,
∴ △ADE ∽△ABC,
∠ADE =∠EFC,∠A =∠CEF,
∴△ADE ∽△EFC.又∵S△ADE : S△EFC = 4 : 9,
∴ AE : EC=2:3,则 AE : AC =2 : 5,
∴ S△ADE : S△ABC = 4 : 25,∴ S△ABC = 25.
拓展与延伸
6. 如图,△ABC 中,DE∥BC,DE 分别交 AB、AC 于
点 D、E,S△ADE=2 S△DCE,求 S△ADE ∶S△ABC.
A
B
C
D
E
【解析】
从题干分析可以得到△ADE∽△ABC,
要证明它们面积的比,直接的就是先求出相似比,
观察得到△ADE与△DCE是同高,
得到AE与CE的比,进而求解.
拓展与延伸
∴
即 S△ADE : S△ABC =4 : 9.
解:过点 D 作 AC 的垂线,交点为 F,则
∴
又∵ DE∥BC,∴ △ADE ∽△ABC.
A
B
C
D
E
F
THANKS
27.2 相似三角形
27.2.2 相似三角形的性质
目
录
CONTENTS
1 学习目标
2 新课导入
3 新课讲解
4 课堂小结
5 当堂小练
6 拓展与延伸
1. 理解并掌握相似三角形中对应线段的比等于相似比,并运用其解决问题. (重点、难点)
2. 理解相似三角形面积的比等于相似比的平方,并运用其解决问题. (重点)
学习目标
新课导入
情景导入
三角形除了三个角,三条边外,还有哪些要素?
高
中线
角平分线
周长
面积
如果两个三角形相似,那
么,对应的这些要素
有什么关系呢?
新课讲解
知识点1 相似三角形对应线段的比
合作探究
如图,△ABC ∽△A′B′C′,相似比为 k,它们对应高、对应中线、对应角平分线的比各是多少?
A
B
C
A'
B'
C'
新课讲解
∵△ABC ∽△A′B′C′,
∴∠B=∠B' ,
解:如图,分别作出 △ABC 和
△A' B' C' 的高 AD 和 A' D' .
则∠ADB =∠A' D' B'=90°.
∴△ABD ∽△A' B' D' .
A
B
C
A'
B'
C'
D'
D
∴
如图,△ABC ∽△A′B′C′,相似比为 k,求它们对应高的比.
新课讲解
试一试
仿照求高的比的过程,当△ABC ∽△A′B′C′,相似比为 k 时,求它们对应中线的比、对应角平分线的比.
新课讲解
结论
由此我们可以得到:
相似三角形对应高的比等于相似比.
类似地,可以证明:
相似三角形对应中线、角平分线的比也等于相似比.
一般地,我们有:
相似三角形对应线段的比等于相似比.
新课讲解
例
典例分析
解:∵ △ABC ∽△DEF,
D
E
F
H
已知 △ABC∽△DEF,BG、EH 分别是 △ABC和 △DEF 的角平分线,BC = 6 cm,EF = 4 cm,BG= 4.8 cm. 求 EH 的长.
∴
(相似三角形对应角平分线的比等于相似比),
∴ ,解得 EH = 3.2.
A
G
B
C
∴ EH 的长为 3.2 cm.
新课讲解
练一练
1. 如果两个相似三角形的对应高的比为 2 : 3,那么对 应角平分线的比是 ,对应边上的中线的比是 ______ .
2. 已知△ABC ∽ △A'B'C' ,相似比为3 : 4,若 BC 边上的高 AD=12 cm,则 B'C' 边上的高 A'D' =______ .
2 : 3
2 : 3
16 cm
新课讲解
想一想:
相似三角形的周长比也等于相似比吗?为什么?
新课讲解
如果 △ABC ∽△A'B'C',相似比为 k,那么
因此
AB=k A'B',BC=kB'C',CA=kC'A',
从而
结论
相似三角形周长的比等于相似比.
新课讲解
知识点2 相似三角形面积的比
合作探究
如图,△ABC ∽△A′B′C′,相似比为 k,它们的面积比是多少?
A
B
C
A'
B'
C'
新课讲解
由前面的结论,我们有
A
B
C
A'
B'
C'
D'
D
新课讲解
结论
相似三角形面积的比等于相似比的平方.
新课讲解
典例分析
1. 已知两个三角形相似,请完成下列表格:
相似比
2
k
……
周长比
……
面积比
10000
……
2
4
100
100
k
k2
新课讲解
练一练
2. 把一个三角形变成和它相似的三角形,
(1) 如果边长扩大为原来的 5 倍,那么面积扩大为 原来的______倍;
(2) 如果面积扩大为原来的 100 倍,那么边长扩大为原来的_____倍.
25
10
新课讲解
练一练
3. 两个相似三角形的一对对应边分别是 35 cm、14 cm,
(1) 它们的周长差为 60 cm,这两个三角形的周长分别________________;
(2) 它们的面积之和是 58 cm2,这两个三角形的面积分别是______________.
100 cm、40 cm
50 cm2、8 cm2
新课讲解
练一练
如图,D,E 分别是 AC,AB 上的点,已知△ABC 的面积为100 cm2,且 ,求四边形 BCDE 的面积.
∴ △ADE ∽△ABC.
∵ 它们的相似比为 3 : 5,∴ 面积比为 9 : 25.
B
C
A
D
E
解:∵ ∠BAC = ∠DAE,且
又∵ △ABC 的面积为 100 cm2,
∴ △ADE 的面积为 36 cm2 .
∴ 四边形 BCDE 的面积为100-36 = 64 (cm2).
课堂小结
相似三角形性质的运用
相似三角形面积的比等于相似比的平方
相似三角形的性质
相似三角形对应线段的比等于相似比
当堂小练
1. 判断:
(1) 一个三角形的各边长扩大为原来的 5 倍,这个
三角形的周长也扩大为原来的 5 倍 ( )
(2) 一个四边形的各边长扩大为原来的 9 倍,这个
四边形的面积也扩大为原来的 9 倍 ( )
√
×
当堂小练
3. 连接三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积 比等于_____.
1 : 2
1 : 4
2. 在 △ABC 和 △DEF 中,AB=2 DE,AC=2 DF,∠A=∠D,AP,DQ 是中线,若 AP=2,则 DQ的值为 ( )
A.2 B.4 C.1 D.
C
当堂小练
4. 两个相似三角形对应的中线长分别是 6 cm 和 18 cm,若较大三角形的周长是 42 cm,面积是 12 cm2,则较小三角形的周长____cm,面积为____cm2.
14
当堂小练
5. △ABC 中,DE∥BC,EF∥AB,已知 △ADE 和
△EFC 的面积分别为 4 和 9,求 △ABC 的面积.
A
B
C
D
F
E
解:∵ DE∥BC,EF∥AB,
∴ △ADE ∽△ABC,
∠ADE =∠EFC,∠A =∠CEF,
∴△ADE ∽△EFC.又∵S△ADE : S△EFC = 4 : 9,
∴ AE : EC=2:3,则 AE : AC =2 : 5,
∴ S△ADE : S△ABC = 4 : 25,∴ S△ABC = 25.
拓展与延伸
6. 如图,△ABC 中,DE∥BC,DE 分别交 AB、AC 于
点 D、E,S△ADE=2 S△DCE,求 S△ADE ∶S△ABC.
A
B
C
D
E
【解析】
从题干分析可以得到△ADE∽△ABC,
要证明它们面积的比,直接的就是先求出相似比,
观察得到△ADE与△DCE是同高,
得到AE与CE的比,进而求解.
拓展与延伸
∴
即 S△ADE : S△ABC =4 : 9.
解:过点 D 作 AC 的垂线,交点为 F,则
∴
又∵ DE∥BC,∴ △ADE ∽△ABC.
A
B
C
D
E
F
THANKS
