北师大版八年级数学下册1.4角平分线专项选择训练(二)(Word版,附答案解析)
文档属性
| 名称 | 北师大版八年级数学下册1.4角平分线专项选择训练(二)(Word版,附答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 208.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-14 00:00:00 | ||
图片预览



文档简介
北师大版八年级数学下册第1章《三角形的证明》
角平分线专项训练(二)
1.如图,在Rt△ABC中,∠A=90°,∠ABC=2∠C,以顶点B为圆心,适当长为半径画弧,分别交边AB,BC于点E,F;再分别以E,F为圆心,以大于EF为半径作弧,两弧在∠ABC内交于点P;作射线BP,交边AC于点G,若AG=,则△GBC的面积为( )
A.3 B.6 C.2 D.
2.如图,∠MON=60°.①以点O为圆心,2cm长为半径画弧,分别交OM、ON于点A、C;②在分别以A、C为圆心,2cm长为半径画弧,两弧交于点B;③连结AB、BC,则四边形OABC的面积为( )
A.4cm2 B.2cm2 C.4cm2 D.2cm2
3.如图,在△ABC中,∠BAC=120°,点E,F分别是△ABC的边AB、AC的中点,边BC分别与DE、DF相交于点H,G,且DE⊥AB,DF⊥AC,连接AD、AG、AH,现在下列四个结论:
①∠EDF=60°,②AD平分∠GAH,③∠B=∠ADF,④GD=GH.
则其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
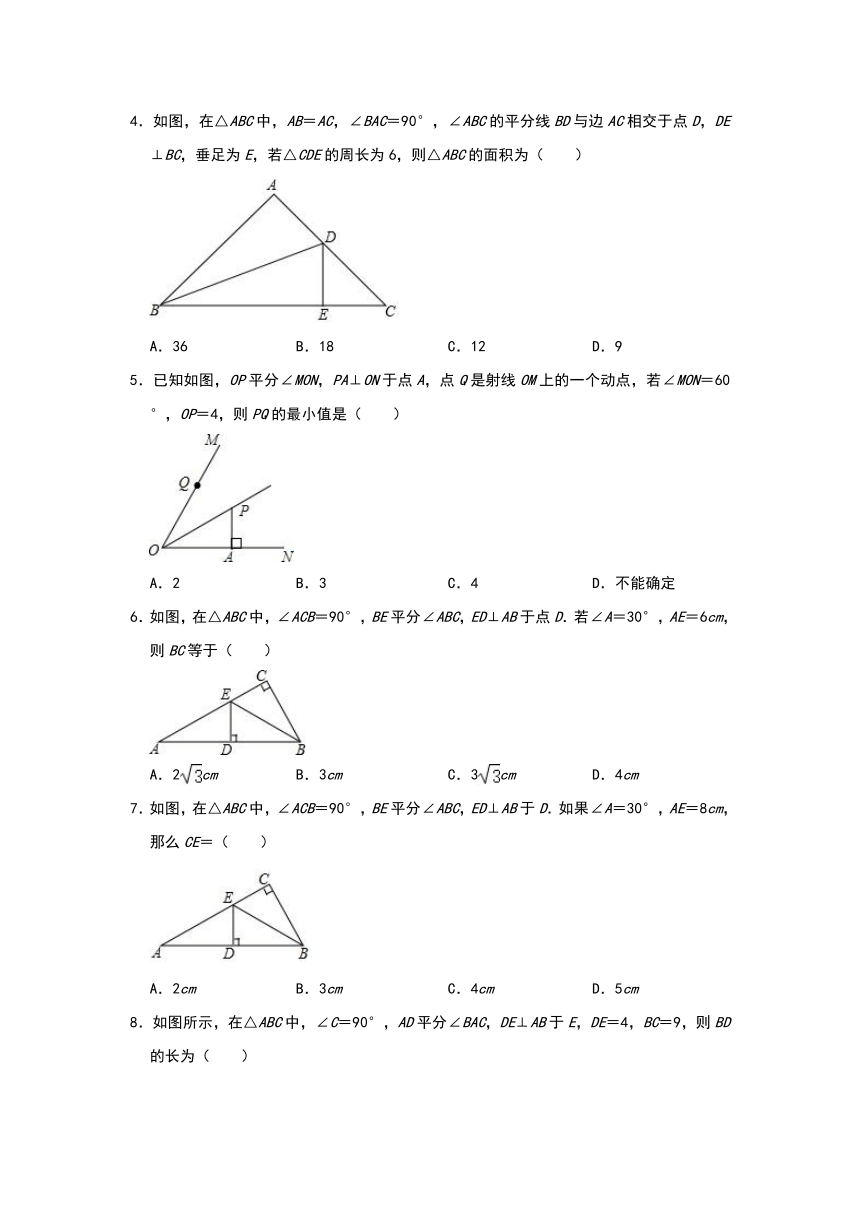
4.如图,在△ABC中,AB=AC,∠BAC=90°,∠ABC的平分线BD与边AC相交于点D,DE⊥BC,垂足为E,若△CDE的周长为6,则△ABC的面积为( )
A.36 B.18 C.12 D.9
5.已知如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若∠MON=60°,OP=4,则PQ的最小值是( )
A.2 B.3 C.4 D.不能确定
6.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于点D.若∠A=30°,AE=6cm,则BC等于( )
A.2cm B.3cm C.3cm D.4cm
7.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=8cm,那么CE=( )
A.2cm B.3cm C.4cm D.5cm
8.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6 B.5 C.4 D.3
9.如图,在Rt△ABC中,其中∠A=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知DC=5,AD=2,则图中长度为的线段有( )
A.1条 B.2条 C.3条 D.4条
10.如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AC=10cm,则△DBE的周长为( )
A.10 B.15 C.10 D.20
11.如图,D为∠BAC的外角平分线上一点并且满足BD=CD,∠DBC=∠DCB,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:
①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
12.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若CD=BD,点D到边AB的距离为6,则BC的长是( )
A.6 B.12 C.18 D.24
13.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④AD平分∠CDE;其中正确的是( )个.
A.1 B.2 C.3 D.4
14.已知△ABC,求作一点P,使点P到∠CAB的两边的距离相等,且P到A、B两点的距离也相等.下列确定点P位置的方法正确的是( )
A.P为∠CAB、∠CBA两角平分线的交点
B.P为AC、AB两边的垂直平分线的交点
C.P为∠CAB的平分线与AB的垂直平分线的交点
D.P为AC、AB两边上的高的交点
15.如图,直线l1,l2,l3表示三条公路.现要建造一个中转站P,使P到三条公路的距离都相等,则中转站P可选择的点有( )
A.一处 B.二处 C.三处 D.四处
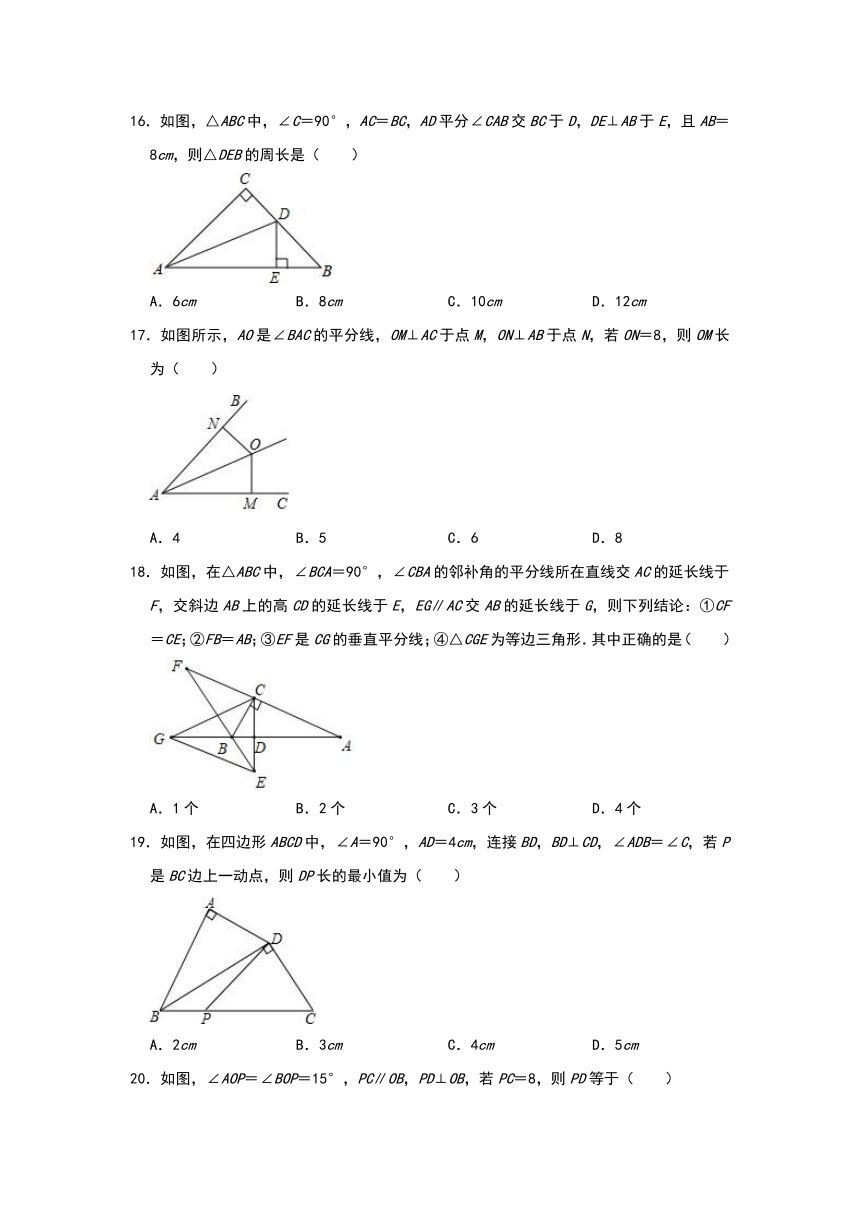
16.如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=8cm,则△DEB的周长是( )
A.6cm B.8cm C.10cm D.12cm
17.如图所示,AO是∠BAC的平分线,OM⊥AC于点M,ON⊥AB于点N,若ON=8,则OM长为( )
A.4 B.5 C.6 D.8
18.如图,在△ABC中,∠BCA=90°,∠CBA的邻补角的平分线所在直线交AC的延长线于F,交斜边AB上的高CD的延长线于E,EG∥AC交AB的延长线于G,则下列结论:①CF=CE;②FB=AB;③EF是CG的垂直平分线;④△CGE为等边三角形.其中正确的是( )
A.1个 B.2个 C.3个 D.4个
19.如图,在四边形ABCD中,∠A=90°,AD=4cm,连接BD,BD⊥CD,∠ADB=∠C,若P是BC边上一动点,则DP长的最小值为( )
A.2cm B.3cm C.4cm D.5cm
20.如图,∠AOP=∠BOP=15°,PC∥OB,PD⊥OB,若PC=8,则PD等于( )
A.4 B.3 C.2 D.1
参考答案
1.解:作GH⊥BC于H,如图,
由作法得BP平分∠ABC,
∴GA=GH=,
∵∠A=90°,∠ABC=2∠C,
∴∠ABC=60°,∠C=30°,
在Rt△ABG,∵∠ABG=∠ABC=30°,
∴AB=AG=3,
在Rt△ABC中,BC=2AB=6,
∴S△BCG=×6×=3.
故选:A.
2.解:由题意可知OB是∠MON的角平分线,
∵∠MON=60°,
∴∠BON=30°,
作BD⊥ON于D,
∵OC=BC=2,
∴∠BOC=∠OBC=30°,
∴∠BCN=60°,
∴BD=BC=,
∴S△BOC=OC×BD==,
∴四边形OABC的面积=2S△BOC=2,
故选:B.
3.解:①∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
∵∠BAC=120°,
∴∠EDF=360°﹣∠AED﹣∠AFD﹣∠BAC=60°,
∴①的结论正确;
②连接BD、CD,如图1,
∵点E,F分别是△ABC的边AB、AC的中点,且DE⊥AB,DF⊥AC,
∴HB=HA,GA=GC,DB=DA=DC,
∴∠ABH=∠BAH,∠ACG=∠CAG,∠DBA=∠DAB,∠DCA=∠DAC,∠DCB=∠DBC,
∴∠DAH=∠DBH=∠DCG=∠DAG
∴AD平分∠HAG,
∴②的结论正确;
③∵点E,F分别是△ABC的边AB、AC的中点,DE⊥AB,DF⊥AC,
∴HB=HA,GA=GC,
∴∠HBA=∠HAB,∠GAC=∠C,
∵∠BAC=120°,
∴∠B+∠C=∠HAB+∠GAC=60°,
∴∠HAG=60°,
∵AD平分∠GAH,
∴∠DAH=∠DAG=30°,
∴∠BAH+∠DAF=90°,
∵∠ADF+∠DAF=90°,
∴∠BAH=∠ADF,
∴∠B=∠ADF,
∴③的结论正确;
④∵DE⊥AB,DF⊥AC,
∴∠DHG=∠BHE=90°﹣∠B,
∠DGH=∠CGF=90°﹣∠C,
当AB≠AC时,用∠B≠∠C,
∴∠DHG≠∠DGH,
∴DH≠DG,
∵∠HDG=60°,
∴△DHG不是等边三角形,
∴GD≠GH,
∴④的结论不正确.
故选:C.
4.解:∵在△ABC中,AB=AC,∠BAC=90°,
∴∠C=∠ABC=45°,
∵DE⊥BC,
∴∠DEC=90°,
∴∠EDC=∠C=45°,
∴DE=EC,
∵BD平分∠BAC,∠A=90°,DE⊥BC,
∴AD=DE,
设DE=AD=CE=x,
由勾股定理得:DC=x,
∵△CDE的周长为6,
∴DE+EC+DC=6,
即x+x+x=6,
解得:x=6﹣3,
即AB=AC=AD+DC=6﹣3+(6﹣3)=3,
∴△ABC的面积为==9,
故选:D.
5.解:作PQ′⊥OM于Q′,
∵∠MON=60°,OP平分∠MON,
∴∠POQ′=30°,
∴PQ′=OP=2,
由垂线段最短可知,PQ的最小值是2,
故选:A.
6.解:在Rt△ADE中,∠A=30°,
∴DE=AE=3,∠ABC=60°,
∵BE平分∠ABC,ED⊥AB,∠ACB=90°,
∴CE=DE=3,∠EBC=30°,
在Rt△CBE中,BC==3(cm),
故选:C.
7.解:∵BE平分∠ABC,ED⊥AB,EC⊥AC,
∴ED=EC,
在Rt△ADE中,∵∠A=30°,
∴ED=AE=×8=4,
∴CE=4cm.
故选:C.
8.解:∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DC=DE=4,
∴BD=BC﹣CD=9﹣4=5.
故选:B.
9.解:∵∠ABC的平分线BD交AC于点D,DE⊥BC,
∴DE=DA=2,
∵DE是BC的垂直平分线,
∴DB=DC=5,BE=CE,
在Rt△ABD中,AB==;
在Rt△BDE中,BE==;
∴CE=.
故选:C.
10.解:∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC,
∴△DBE的周长=DE+DC+BD=DC+DB+BE=BC+BE,
在Rt△ACD和Rt△AED中
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∵∠C=90°,AC=BC,
∴AB=AC=10cm.
∴△DBE的周长=AE+BE=AB=10cm.
故选:C.
11.解:∵AD平分∠CAF,DE⊥AC,DF⊥AB,
∴DE=DF,
在Rt△CDE和Rt△BDF中,
,
∴Rt△CDE≌Rt△BDF(HL),故①正确;
∴CE=AF,
在Rt△ADE和Rt△ADF中,
,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,
∴CE=AB+AF=AB+AE,故②正确;
∵Rt△CDE≌Rt△BDF,
∴∠DBF=∠DCE,
∵∠AOB=∠COD,(设AC交BD于O),
∴∠BDC=∠BAC,故③正确;
∵△CDE≌△BDF,
∴∠ABO=∠DCO,
∴A,B,C,D四点共圆,
∴∠DAE=∠CBD,
∵Rt△ADE≌Rt△ADF,
∴∠DAE=∠DAF,
∴∠DAF=∠CBD,故④正确;
综上所述,正确的结论有①②③④共4个.
故选:D.
12.解:
过D作DE⊥AB于E,
∵点D到边AB的距离为6,
∴DE=6,
∵∠C=90°,AD平分∠BAC,DE⊥AB,
∴CD=DE=6,
∵CD=DB,
∴DB=12,
∴BC=6+12=18,
故选:C.
13.解:∵∠C=90°,AD平分∠BAC,DE⊥AB,
∴CD=DE,故①正确;
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,∠ADC=∠ADE,
∴AC+BE=AE+BE=AB,故②正确;
AD平分∠CDE,故④正确;
∵∠B+∠BAC=90°,
∠B+∠BDE=90°,
∴∠BDE=∠BAC,故③正确;
综上所述,结论正确的是①②③④共4个.
故选:D.
14.解:∵点P到∠CAB的两边的距离相等,
∴点P在∠CAB的平分线上,
∵点P到A、B两点的距离也相等,
∴点P在A线段B的垂直平分线上,
∴P为∠CAB的平分线与AB的垂直平分线的交点.
故选:C.
15.解:满足条件的有:
(1)三角形两个内角平分线的交点,共一处;
(2)三个外角两两平分线的交点,共三处.
故选:D.
16.解:∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴CD=DE,
∴AC=AE,
∴△DEB的周长=BD+DE+BE,
=BD+CD+BE,
=BC+BE,
=AC+BE,
=AE+BE,
=AB,
∵AB=8cm,
∴△DEB的周长是8cm.
故选:B.
17.解:∵AO是∠BAC的平分线,OM⊥AC,ON⊥AB,
∴OM=ON=8,
故选:D.
18.解:∵BF平分∠GBC,
∴∠GBF=∠CBF,
而∠GBF=∠EBD,
∴∠CBF=∠EBD,
∵∠BCA=90°,CD为高,
∴∠F=∠BED,
∴CF=CE,所以①正确
在△EGC中,
EC=EG,BE平分∠CEG,
∴EB垂直平分GC,所以③正确;
而选项②④由题干条件不能证明得出,所以①③正确;
故选:B.
19.解:根据垂线段最短,当DP⊥BC的时候,DP的长度最小,
∵BD⊥CD,即∠BDC=90°,又∠A=90°,
∴∠A=∠BDC,又∠ADB=∠C,
∴∠ABD=∠CBD,又DA⊥BA,BD⊥DC,
∴AD=DP,又AD=4cm,
∴DP=4cm.
故选:C.
20.解:作PE⊥OA于E,
∵∠AOP=∠BOP=15°,
∴∠AOB=30°,
∵PC∥OB,
∴∠ACP=∠AOB=30°,
∴PE=PC=4,
∵OP是∠AOB的平分线,PD⊥OB,PE⊥OA,
∴PD=PE=4,
故选:A.
角平分线专项训练(二)
1.如图,在Rt△ABC中,∠A=90°,∠ABC=2∠C,以顶点B为圆心,适当长为半径画弧,分别交边AB,BC于点E,F;再分别以E,F为圆心,以大于EF为半径作弧,两弧在∠ABC内交于点P;作射线BP,交边AC于点G,若AG=,则△GBC的面积为( )
A.3 B.6 C.2 D.
2.如图,∠MON=60°.①以点O为圆心,2cm长为半径画弧,分别交OM、ON于点A、C;②在分别以A、C为圆心,2cm长为半径画弧,两弧交于点B;③连结AB、BC,则四边形OABC的面积为( )
A.4cm2 B.2cm2 C.4cm2 D.2cm2
3.如图,在△ABC中,∠BAC=120°,点E,F分别是△ABC的边AB、AC的中点,边BC分别与DE、DF相交于点H,G,且DE⊥AB,DF⊥AC,连接AD、AG、AH,现在下列四个结论:
①∠EDF=60°,②AD平分∠GAH,③∠B=∠ADF,④GD=GH.
则其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
4.如图,在△ABC中,AB=AC,∠BAC=90°,∠ABC的平分线BD与边AC相交于点D,DE⊥BC,垂足为E,若△CDE的周长为6,则△ABC的面积为( )
A.36 B.18 C.12 D.9
5.已知如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若∠MON=60°,OP=4,则PQ的最小值是( )
A.2 B.3 C.4 D.不能确定
6.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于点D.若∠A=30°,AE=6cm,则BC等于( )
A.2cm B.3cm C.3cm D.4cm
7.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=8cm,那么CE=( )
A.2cm B.3cm C.4cm D.5cm
8.如图所示,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,DE=4,BC=9,则BD的长为( )
A.6 B.5 C.4 D.3
9.如图,在Rt△ABC中,其中∠A=90°,∠ABC的平分线BD交AC于点D,DE是BC的垂直平分线,点E是垂足.已知DC=5,AD=2,则图中长度为的线段有( )
A.1条 B.2条 C.3条 D.4条
10.如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E,若AC=10cm,则△DBE的周长为( )
A.10 B.15 C.10 D.20
11.如图,D为∠BAC的外角平分线上一点并且满足BD=CD,∠DBC=∠DCB,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:
①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
12.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若CD=BD,点D到边AB的距离为6,则BC的长是( )
A.6 B.12 C.18 D.24
13.如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④AD平分∠CDE;其中正确的是( )个.
A.1 B.2 C.3 D.4
14.已知△ABC,求作一点P,使点P到∠CAB的两边的距离相等,且P到A、B两点的距离也相等.下列确定点P位置的方法正确的是( )
A.P为∠CAB、∠CBA两角平分线的交点
B.P为AC、AB两边的垂直平分线的交点
C.P为∠CAB的平分线与AB的垂直平分线的交点
D.P为AC、AB两边上的高的交点
15.如图,直线l1,l2,l3表示三条公路.现要建造一个中转站P,使P到三条公路的距离都相等,则中转站P可选择的点有( )
A.一处 B.二处 C.三处 D.四处
16.如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=8cm,则△DEB的周长是( )
A.6cm B.8cm C.10cm D.12cm
17.如图所示,AO是∠BAC的平分线,OM⊥AC于点M,ON⊥AB于点N,若ON=8,则OM长为( )
A.4 B.5 C.6 D.8
18.如图,在△ABC中,∠BCA=90°,∠CBA的邻补角的平分线所在直线交AC的延长线于F,交斜边AB上的高CD的延长线于E,EG∥AC交AB的延长线于G,则下列结论:①CF=CE;②FB=AB;③EF是CG的垂直平分线;④△CGE为等边三角形.其中正确的是( )
A.1个 B.2个 C.3个 D.4个
19.如图,在四边形ABCD中,∠A=90°,AD=4cm,连接BD,BD⊥CD,∠ADB=∠C,若P是BC边上一动点,则DP长的最小值为( )
A.2cm B.3cm C.4cm D.5cm
20.如图,∠AOP=∠BOP=15°,PC∥OB,PD⊥OB,若PC=8,则PD等于( )
A.4 B.3 C.2 D.1
参考答案
1.解:作GH⊥BC于H,如图,
由作法得BP平分∠ABC,
∴GA=GH=,
∵∠A=90°,∠ABC=2∠C,
∴∠ABC=60°,∠C=30°,
在Rt△ABG,∵∠ABG=∠ABC=30°,
∴AB=AG=3,
在Rt△ABC中,BC=2AB=6,
∴S△BCG=×6×=3.
故选:A.
2.解:由题意可知OB是∠MON的角平分线,
∵∠MON=60°,
∴∠BON=30°,
作BD⊥ON于D,
∵OC=BC=2,
∴∠BOC=∠OBC=30°,
∴∠BCN=60°,
∴BD=BC=,
∴S△BOC=OC×BD==,
∴四边形OABC的面积=2S△BOC=2,
故选:B.
3.解:①∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
∵∠BAC=120°,
∴∠EDF=360°﹣∠AED﹣∠AFD﹣∠BAC=60°,
∴①的结论正确;
②连接BD、CD,如图1,
∵点E,F分别是△ABC的边AB、AC的中点,且DE⊥AB,DF⊥AC,
∴HB=HA,GA=GC,DB=DA=DC,
∴∠ABH=∠BAH,∠ACG=∠CAG,∠DBA=∠DAB,∠DCA=∠DAC,∠DCB=∠DBC,
∴∠DAH=∠DBH=∠DCG=∠DAG
∴AD平分∠HAG,
∴②的结论正确;
③∵点E,F分别是△ABC的边AB、AC的中点,DE⊥AB,DF⊥AC,
∴HB=HA,GA=GC,
∴∠HBA=∠HAB,∠GAC=∠C,
∵∠BAC=120°,
∴∠B+∠C=∠HAB+∠GAC=60°,
∴∠HAG=60°,
∵AD平分∠GAH,
∴∠DAH=∠DAG=30°,
∴∠BAH+∠DAF=90°,
∵∠ADF+∠DAF=90°,
∴∠BAH=∠ADF,
∴∠B=∠ADF,
∴③的结论正确;
④∵DE⊥AB,DF⊥AC,
∴∠DHG=∠BHE=90°﹣∠B,
∠DGH=∠CGF=90°﹣∠C,
当AB≠AC时,用∠B≠∠C,
∴∠DHG≠∠DGH,
∴DH≠DG,
∵∠HDG=60°,
∴△DHG不是等边三角形,
∴GD≠GH,
∴④的结论不正确.
故选:C.
4.解:∵在△ABC中,AB=AC,∠BAC=90°,
∴∠C=∠ABC=45°,
∵DE⊥BC,
∴∠DEC=90°,
∴∠EDC=∠C=45°,
∴DE=EC,
∵BD平分∠BAC,∠A=90°,DE⊥BC,
∴AD=DE,
设DE=AD=CE=x,
由勾股定理得:DC=x,
∵△CDE的周长为6,
∴DE+EC+DC=6,
即x+x+x=6,
解得:x=6﹣3,
即AB=AC=AD+DC=6﹣3+(6﹣3)=3,
∴△ABC的面积为==9,
故选:D.
5.解:作PQ′⊥OM于Q′,
∵∠MON=60°,OP平分∠MON,
∴∠POQ′=30°,
∴PQ′=OP=2,
由垂线段最短可知,PQ的最小值是2,
故选:A.
6.解:在Rt△ADE中,∠A=30°,
∴DE=AE=3,∠ABC=60°,
∵BE平分∠ABC,ED⊥AB,∠ACB=90°,
∴CE=DE=3,∠EBC=30°,
在Rt△CBE中,BC==3(cm),
故选:C.
7.解:∵BE平分∠ABC,ED⊥AB,EC⊥AC,
∴ED=EC,
在Rt△ADE中,∵∠A=30°,
∴ED=AE=×8=4,
∴CE=4cm.
故选:C.
8.解:∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DC=DE=4,
∴BD=BC﹣CD=9﹣4=5.
故选:B.
9.解:∵∠ABC的平分线BD交AC于点D,DE⊥BC,
∴DE=DA=2,
∵DE是BC的垂直平分线,
∴DB=DC=5,BE=CE,
在Rt△ABD中,AB==;
在Rt△BDE中,BE==;
∴CE=.
故选:C.
10.解:∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC,
∴△DBE的周长=DE+DC+BD=DC+DB+BE=BC+BE,
在Rt△ACD和Rt△AED中
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,
∵∠C=90°,AC=BC,
∴AB=AC=10cm.
∴△DBE的周长=AE+BE=AB=10cm.
故选:C.
11.解:∵AD平分∠CAF,DE⊥AC,DF⊥AB,
∴DE=DF,
在Rt△CDE和Rt△BDF中,
,
∴Rt△CDE≌Rt△BDF(HL),故①正确;
∴CE=AF,
在Rt△ADE和Rt△ADF中,
,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,
∴CE=AB+AF=AB+AE,故②正确;
∵Rt△CDE≌Rt△BDF,
∴∠DBF=∠DCE,
∵∠AOB=∠COD,(设AC交BD于O),
∴∠BDC=∠BAC,故③正确;
∵△CDE≌△BDF,
∴∠ABO=∠DCO,
∴A,B,C,D四点共圆,
∴∠DAE=∠CBD,
∵Rt△ADE≌Rt△ADF,
∴∠DAE=∠DAF,
∴∠DAF=∠CBD,故④正确;
综上所述,正确的结论有①②③④共4个.
故选:D.
12.解:
过D作DE⊥AB于E,
∵点D到边AB的距离为6,
∴DE=6,
∵∠C=90°,AD平分∠BAC,DE⊥AB,
∴CD=DE=6,
∵CD=DB,
∴DB=12,
∴BC=6+12=18,
故选:C.
13.解:∵∠C=90°,AD平分∠BAC,DE⊥AB,
∴CD=DE,故①正确;
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,∠ADC=∠ADE,
∴AC+BE=AE+BE=AB,故②正确;
AD平分∠CDE,故④正确;
∵∠B+∠BAC=90°,
∠B+∠BDE=90°,
∴∠BDE=∠BAC,故③正确;
综上所述,结论正确的是①②③④共4个.
故选:D.
14.解:∵点P到∠CAB的两边的距离相等,
∴点P在∠CAB的平分线上,
∵点P到A、B两点的距离也相等,
∴点P在A线段B的垂直平分线上,
∴P为∠CAB的平分线与AB的垂直平分线的交点.
故选:C.
15.解:满足条件的有:
(1)三角形两个内角平分线的交点,共一处;
(2)三个外角两两平分线的交点,共三处.
故选:D.
16.解:∵AD平分∠CAB,∠C=90°,DE⊥AB,
∴CD=DE,
∴AC=AE,
∴△DEB的周长=BD+DE+BE,
=BD+CD+BE,
=BC+BE,
=AC+BE,
=AE+BE,
=AB,
∵AB=8cm,
∴△DEB的周长是8cm.
故选:B.
17.解:∵AO是∠BAC的平分线,OM⊥AC,ON⊥AB,
∴OM=ON=8,
故选:D.
18.解:∵BF平分∠GBC,
∴∠GBF=∠CBF,
而∠GBF=∠EBD,
∴∠CBF=∠EBD,
∵∠BCA=90°,CD为高,
∴∠F=∠BED,
∴CF=CE,所以①正确
在△EGC中,
EC=EG,BE平分∠CEG,
∴EB垂直平分GC,所以③正确;
而选项②④由题干条件不能证明得出,所以①③正确;
故选:B.
19.解:根据垂线段最短,当DP⊥BC的时候,DP的长度最小,
∵BD⊥CD,即∠BDC=90°,又∠A=90°,
∴∠A=∠BDC,又∠ADB=∠C,
∴∠ABD=∠CBD,又DA⊥BA,BD⊥DC,
∴AD=DP,又AD=4cm,
∴DP=4cm.
故选:C.
20.解:作PE⊥OA于E,
∵∠AOP=∠BOP=15°,
∴∠AOB=30°,
∵PC∥OB,
∴∠ACP=∠AOB=30°,
∴PE=PC=4,
∵OP是∠AOB的平分线,PD⊥OB,PE⊥OA,
∴PD=PE=4,
故选:A.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
