等式的性质
图片预览






文档简介
(共21张PPT)
①4+x=7, ② 2x, ③ 3x+1,
④ a+b=b+a, ⑤ a2+b2 ⑥ c=2πr
2
3
⑦ 1+2=3, ⑧ ab, ⑨ S= ah,
⑩ 2x-3y
1
2
上述这组式子中,( )是等式, ( ) 不是等式,为什么?
①④⑥⑦⑨
②③⑤⑧⑩
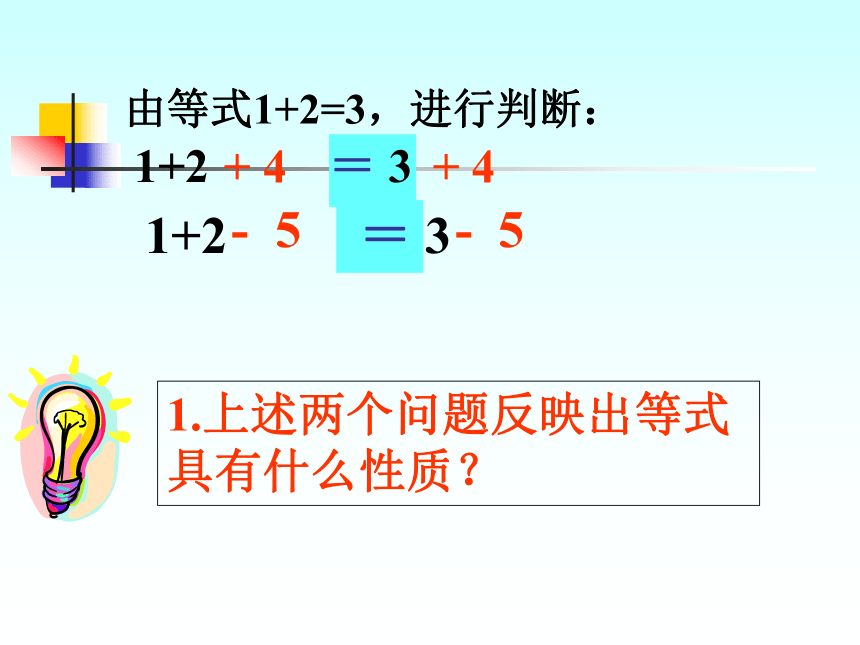
由等式1+2=3,进行判断:
+ 4
+ 4
1+2 = 3
- 5
- 5
1.上述两个问题反映出等式具有什么性质?
1+2 = 3
等式的两边都加上(或减去)同
一个数所得的结果仍是等式.
由等式2x+3x=5x,进行判断:
+ 4x
+ 4x
2x+3x = 5x
- x
- x
2x+3x = 5x
1.上述两个问题反映出等式具有什么性质?
等式的两边都加上(或减去)同一个数或同一个式子,所得的结果仍是等式.
等式性质1
用式子的
形式怎样
表示
由等式3m+5m=8m ,进行判断:
2×( )
2×
( )÷2
÷2
2.上述两个问题反映出等式具有什么性质?
3m+5m = 8m
3m+5m = 8m
等式两边都乘以(或除以)同一个数(除数不为零),所得的结果仍是等式.
等式性质2
用式子的
形式怎样
表示
等 式 的 性 质
注意
1、等式两边都要参加运算,并且是作同一种运算。 2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子。
3、等式两边不能都除以0,即0不能作除数或分母.
用等式的性质解方程
解:(1)两边减7得
(2)两边同时除以-5得
(3)两边加5,得
化简得:
两边同乘-3,得
经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的形式:
x = a(常数)
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项.
(6)
(5)
两边同时除以5,得
两边同时减2,得
两边同时乘2,得
两边同除以0.3,得
(4)
8
=
x
两边同时减4,得
2
三、我会应用
根据 。
根据 。
.
(3)、如果4x=-12y,那么x= ,
根据 。
(4)、如果-0.2x=6,那么x= ,
根据 。
(2)、如果x-3=2,那么x-3+3= ,
2x0.5
等式性质2,在等式两边同时乘2
等式性质1,在等式两边同加3
2+3
-3y
等式性质2,在等式两边同时除以4
-30
等式性质2,在等式两边同除以-0.2或乘-5
1 、
2、下列变形符合等式性质的是( )
A、如果2x-3=7,那么2x=7-3
B、如果3x-2=1,那么3x=1-2
C、如果-2x=5,那么x=5+2
3、依据等式性质进行变形,用得不正确的是( )
D
D
4、判断下列说法是否成立,并说明理由
( )
( )
( )
.
(因为x可能等于0)
(等量代换)
(对称性)
6、在学习了等式的性质后,小红发现运用等式的性质可以使复杂的等式变得简洁,这使她异常兴奋,于是她随手写了一个等式:3a+b-2=7a+b-2,并开始运用等式性质对这个等式进行变形,其过程如下:
3a+b=7a+b(等式两边同时加上2)
3a=7a(等式两边同时减去b)
3=7(等式两边同时除以a)
变形到此,小红顿时就傻了:居然得出如此等式!于是小红开始检查自己的变形过程,但怎么也找不出错误来。
聪明的同学,你能让小红的愁眉在恍然大悟中舒展开来吗?
对自己说,你有什么收获?
对老师说,你还有什么困惑?
【等式性质 2】
【等式性质1】
注意
1、等式两边都要参加运算,并且是作同一种运算。 2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子。
3、等式两边不能都除以0,即0不能作除数或分母.
下课了!
①4+x=7, ② 2x, ③ 3x+1,
④ a+b=b+a, ⑤ a2+b2 ⑥ c=2πr
2
3
⑦ 1+2=3, ⑧ ab, ⑨ S= ah,
⑩ 2x-3y
1
2
上述这组式子中,( )是等式, ( ) 不是等式,为什么?
①④⑥⑦⑨
②③⑤⑧⑩
由等式1+2=3,进行判断:
+ 4
+ 4
1+2 = 3
- 5
- 5
1.上述两个问题反映出等式具有什么性质?
1+2 = 3
等式的两边都加上(或减去)同
一个数所得的结果仍是等式.
由等式2x+3x=5x,进行判断:
+ 4x
+ 4x
2x+3x = 5x
- x
- x
2x+3x = 5x
1.上述两个问题反映出等式具有什么性质?
等式的两边都加上(或减去)同一个数或同一个式子,所得的结果仍是等式.
等式性质1
用式子的
形式怎样
表示
由等式3m+5m=8m ,进行判断:
2×( )
2×
( )÷2
÷2
2.上述两个问题反映出等式具有什么性质?
3m+5m = 8m
3m+5m = 8m
等式两边都乘以(或除以)同一个数(除数不为零),所得的结果仍是等式.
等式性质2
用式子的
形式怎样
表示
等 式 的 性 质
注意
1、等式两边都要参加运算,并且是作同一种运算。 2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子。
3、等式两边不能都除以0,即0不能作除数或分母.
用等式的性质解方程
解:(1)两边减7得
(2)两边同时除以-5得
(3)两边加5,得
化简得:
两边同乘-3,得
经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的形式:
x = a(常数)
即方程左边只一个未知数项、且未知数项的系数是 1,右边只一个常数项.
(6)
(5)
两边同时除以5,得
两边同时减2,得
两边同时乘2,得
两边同除以0.3,得
(4)
8
=
x
两边同时减4,得
2
三、我会应用
根据 。
根据 。
.
(3)、如果4x=-12y,那么x= ,
根据 。
(4)、如果-0.2x=6,那么x= ,
根据 。
(2)、如果x-3=2,那么x-3+3= ,
2x0.5
等式性质2,在等式两边同时乘2
等式性质1,在等式两边同加3
2+3
-3y
等式性质2,在等式两边同时除以4
-30
等式性质2,在等式两边同除以-0.2或乘-5
1 、
2、下列变形符合等式性质的是( )
A、如果2x-3=7,那么2x=7-3
B、如果3x-2=1,那么3x=1-2
C、如果-2x=5,那么x=5+2
3、依据等式性质进行变形,用得不正确的是( )
D
D
4、判断下列说法是否成立,并说明理由
( )
( )
( )
.
(因为x可能等于0)
(等量代换)
(对称性)
6、在学习了等式的性质后,小红发现运用等式的性质可以使复杂的等式变得简洁,这使她异常兴奋,于是她随手写了一个等式:3a+b-2=7a+b-2,并开始运用等式性质对这个等式进行变形,其过程如下:
3a+b=7a+b(等式两边同时加上2)
3a=7a(等式两边同时减去b)
3=7(等式两边同时除以a)
变形到此,小红顿时就傻了:居然得出如此等式!于是小红开始检查自己的变形过程,但怎么也找不出错误来。
聪明的同学,你能让小红的愁眉在恍然大悟中舒展开来吗?
对自己说,你有什么收获?
对老师说,你还有什么困惑?
【等式性质 2】
【等式性质1】
注意
1、等式两边都要参加运算,并且是作同一种运算。 2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子。
3、等式两边不能都除以0,即0不能作除数或分母.
下课了!
