北师大版七年级数学下册第一章整式的乘除复习课件(共21张PPT)
文档属性
| 名称 | 北师大版七年级数学下册第一章整式的乘除复习课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 165.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-14 22:43:49 | ||
图片预览


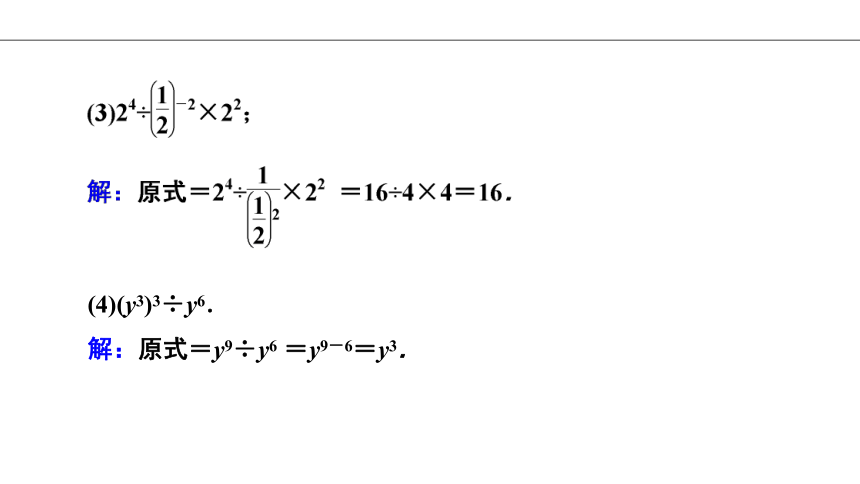




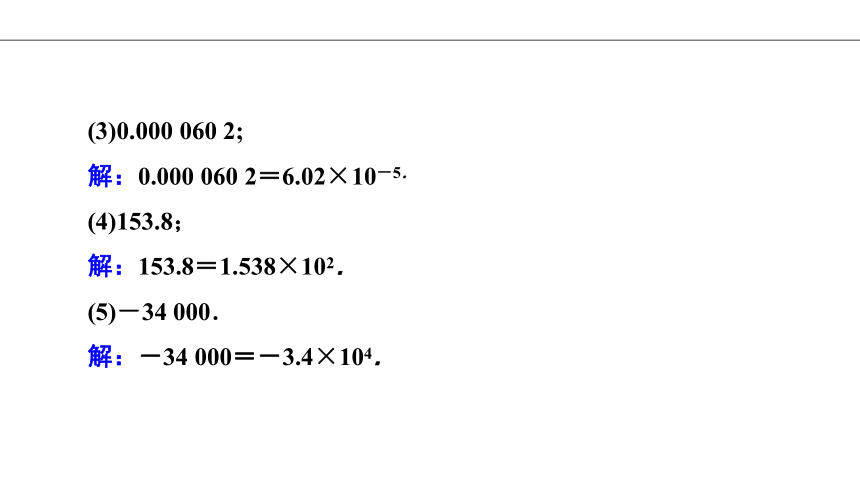

文档简介
第一章 整式的乘除
阶段复习——整式的乘法
知识点1 幂的运算
例1 计算:
(1)(3m)2;
解:原式=32·m2=9m2.
(2)(-2a3b2c)2;
解:原式=(-2)2·(a3)2·(b2)2·c2=4a6b4c2.
(4)(y3)3÷y6.
解:原式=y9÷y6 =y9-6=y3.
1.(2020年贵港港南区期末)下面的计算不正确的是 ( )
A.5a3-a3=4a3 B.2m·3n=6m+n
C.2m·2n=2m+n D.-a2·(-a3)=a5
2.(2020年重庆渝中区期中)计算(-2ab2)3,结果正确的是 ( )
A.-2a3b6 B.-6a3b6
C.-8a3b5 D.-8a3b6
3.已知am=3,an=6,则am+2n的值是_______.
B
D
108
知识点2 用科学记数法表示绝对值较小的数
例2 用科学记数法表示下列各数:
(1)0.000 03;
解:0.000 03=3×10-5.
(2)-0.000 006 4;
解:-0.000 006 4=-6.4×10-6.
(3)0.000 031 4;
解:(3)0.000 031 4=3.14×10-5.
(4)2 013 000.
解:2 013 000 =2.013×106.
4.用科学记数法表示下列各数:
(1)0.060 2;
解:0.060 2 =6.02×10-2.
(2)-0.006 02;
解:-0.006 02 =-6.02×10-3.
(3)0.000 060 2;
解:0.000 060 2=6.02×10-5.
(4)153.8;
解:153.8=1.538×102.
(5)-34 000.
解:-34 000=-3.4×104.
知识点3 整式的乘法
例3 (2020年成都青羊区期末)以下关于x的各个多项式中,a,b,c,m,n均为常数.
(1)根据计算结果填写表格:
项目
二次项系数
一次项系数
常数项
(x+1)(x+2)
1
3
2
(2x-1)(3x+2)
6
1
-2
(ax+b)(mx+n)
am
an+bm
bn
(2)若关于x的代数式(x+2)·(x2+mx+n)化简后,既不含二次项,也不含一次项,求m,n的值.
解:(x+2)(x2+mx+n)=x3+mx2+nx+2x2+2mx+2n=x3+(m+2)x2+(2m+n)x+2n,
∵这个多项式既不含二次项,也不含一次项,
∴m+2=0,2m+n=0.
解得m=-2,n=4.
5.下列各式中,结果等于x2-5x-6的是 ( )
A.(x-6)(x+1) B.(x-2)(x+3)
C.(x+6)(x-1) D.(x-2)(x-3)
A
方法点拨:本题求解的关键是得到二次项与一次项,因此在解题时可以不展开这个乘积式的全部,而只计算x·mx+2·x2=(m+2)x2,x·n+2·mx=(2m+n)x,由此也能求得答案,从而避免了一些不必要的计算.
【第一关】
1.(2020年大同期末)石墨烯是已知强度最高的材料之一,同时还具有很好的韧性,石墨烯的理论厚度为0.000 000 000 34米,这个数据用科学记数法可表示为 ( )
A.0.34×10-9 B.3.4×10-11
C.3.4×10-10 D.3.4×10-9
C
2.下列运算正确的是 ( )
A.3x2+4x2=7x4 B.(-x)-9÷(-x)-3=x-6
C.x2-x2=1 D.-x(x2-x+1)=-x3-x2-x
3.化简:(-a2)·a5=________.
4.(2020年淮安期末)若a·a3·am=a8,则m=_____.
B
-a7
4
5.下面的计算对不对?如果不对,应怎样改正?
(1)(a3b)3=a3b3;
解:原式计算错误,应为(a3b)3=a9b3.
(2)(6xy)2=12x2y2;
解:原式计算错误,应为(6xy)2=36x2y2.
(3)-(3x3)2=9x6;
解:原式计算错误,应为-(3x3)2=-9x6.
(4)(-2ax2)2=-4a2x4.
解:原式计算错误,应为(-2ax2)2=4a2x4.
【第二关】
6.(2020年西安雁塔区期末)下列计算正确的是 ( )
A.(2m2)3=2m5 B.a2+a2+a2=a6
C.-(n2)2=n4 D.2x·5y=10xy
7.(2020年杭州江干区期末)若2x+y-2=0,则52x·5y=______.
D
25
(2)(3m-n)(m+2n);
解:原式=3m2+6mn-mn-2n2=3m2+5mn-2n2.
(4)(-2ab)3-(-ab3)·(3a)2.
解:原式=-8a3b3+ab3·9a2=-8a3b3+9a3b3=a3b3.
9.(2020年常德期中)若(x2+mx-8)(x2-3x+n)的展开式中不含x2和x3项,求m+n的值.
解:原式=x4-3x3+nx2+mx3-3mx2+mnx-8x2+24x-8n=x4+(m-3)x3+(n-3m-8)x2+(mn+24)x-8n,
∵展开式中不含x2和x3项,
∴m-3=0,n-3m-8=0,
解得m=3,n=17.
故m+n=20.
【第三关】
10.若am=an(a>0且a≠1,m,n是正整数),则m=n.利用上面结论解决下面的问题:
(1)若3x·9x·27x=312,求x的值;
(2)若x=3m+2,y=9m+3m,用含x的代数式表示y.
解:(1)原式=3x·(32)x·(33)x=3x·32x·33x=36x.
∵36x=312,∴6x=12,
解得x=2.
(2)∵x=3m+2,∴3m=x-2.
∵y=9m+3m=32m+3m=(3m)2+3m=(x-2)2+x-2=x2-3x+2,
∴y=x2-3x+2.
阶段复习——整式的乘法
知识点1 幂的运算
例1 计算:
(1)(3m)2;
解:原式=32·m2=9m2.
(2)(-2a3b2c)2;
解:原式=(-2)2·(a3)2·(b2)2·c2=4a6b4c2.
(4)(y3)3÷y6.
解:原式=y9÷y6 =y9-6=y3.
1.(2020年贵港港南区期末)下面的计算不正确的是 ( )
A.5a3-a3=4a3 B.2m·3n=6m+n
C.2m·2n=2m+n D.-a2·(-a3)=a5
2.(2020年重庆渝中区期中)计算(-2ab2)3,结果正确的是 ( )
A.-2a3b6 B.-6a3b6
C.-8a3b5 D.-8a3b6
3.已知am=3,an=6,则am+2n的值是_______.
B
D
108
知识点2 用科学记数法表示绝对值较小的数
例2 用科学记数法表示下列各数:
(1)0.000 03;
解:0.000 03=3×10-5.
(2)-0.000 006 4;
解:-0.000 006 4=-6.4×10-6.
(3)0.000 031 4;
解:(3)0.000 031 4=3.14×10-5.
(4)2 013 000.
解:2 013 000 =2.013×106.
4.用科学记数法表示下列各数:
(1)0.060 2;
解:0.060 2 =6.02×10-2.
(2)-0.006 02;
解:-0.006 02 =-6.02×10-3.
(3)0.000 060 2;
解:0.000 060 2=6.02×10-5.
(4)153.8;
解:153.8=1.538×102.
(5)-34 000.
解:-34 000=-3.4×104.
知识点3 整式的乘法
例3 (2020年成都青羊区期末)以下关于x的各个多项式中,a,b,c,m,n均为常数.
(1)根据计算结果填写表格:
项目
二次项系数
一次项系数
常数项
(x+1)(x+2)
1
3
2
(2x-1)(3x+2)
6
1
-2
(ax+b)(mx+n)
am
an+bm
bn
(2)若关于x的代数式(x+2)·(x2+mx+n)化简后,既不含二次项,也不含一次项,求m,n的值.
解:(x+2)(x2+mx+n)=x3+mx2+nx+2x2+2mx+2n=x3+(m+2)x2+(2m+n)x+2n,
∵这个多项式既不含二次项,也不含一次项,
∴m+2=0,2m+n=0.
解得m=-2,n=4.
5.下列各式中,结果等于x2-5x-6的是 ( )
A.(x-6)(x+1) B.(x-2)(x+3)
C.(x+6)(x-1) D.(x-2)(x-3)
A
方法点拨:本题求解的关键是得到二次项与一次项,因此在解题时可以不展开这个乘积式的全部,而只计算x·mx+2·x2=(m+2)x2,x·n+2·mx=(2m+n)x,由此也能求得答案,从而避免了一些不必要的计算.
【第一关】
1.(2020年大同期末)石墨烯是已知强度最高的材料之一,同时还具有很好的韧性,石墨烯的理论厚度为0.000 000 000 34米,这个数据用科学记数法可表示为 ( )
A.0.34×10-9 B.3.4×10-11
C.3.4×10-10 D.3.4×10-9
C
2.下列运算正确的是 ( )
A.3x2+4x2=7x4 B.(-x)-9÷(-x)-3=x-6
C.x2-x2=1 D.-x(x2-x+1)=-x3-x2-x
3.化简:(-a2)·a5=________.
4.(2020年淮安期末)若a·a3·am=a8,则m=_____.
B
-a7
4
5.下面的计算对不对?如果不对,应怎样改正?
(1)(a3b)3=a3b3;
解:原式计算错误,应为(a3b)3=a9b3.
(2)(6xy)2=12x2y2;
解:原式计算错误,应为(6xy)2=36x2y2.
(3)-(3x3)2=9x6;
解:原式计算错误,应为-(3x3)2=-9x6.
(4)(-2ax2)2=-4a2x4.
解:原式计算错误,应为(-2ax2)2=4a2x4.
【第二关】
6.(2020年西安雁塔区期末)下列计算正确的是 ( )
A.(2m2)3=2m5 B.a2+a2+a2=a6
C.-(n2)2=n4 D.2x·5y=10xy
7.(2020年杭州江干区期末)若2x+y-2=0,则52x·5y=______.
D
25
(2)(3m-n)(m+2n);
解:原式=3m2+6mn-mn-2n2=3m2+5mn-2n2.
(4)(-2ab)3-(-ab3)·(3a)2.
解:原式=-8a3b3+ab3·9a2=-8a3b3+9a3b3=a3b3.
9.(2020年常德期中)若(x2+mx-8)(x2-3x+n)的展开式中不含x2和x3项,求m+n的值.
解:原式=x4-3x3+nx2+mx3-3mx2+mnx-8x2+24x-8n=x4+(m-3)x3+(n-3m-8)x2+(mn+24)x-8n,
∵展开式中不含x2和x3项,
∴m-3=0,n-3m-8=0,
解得m=3,n=17.
故m+n=20.
【第三关】
10.若am=an(a>0且a≠1,m,n是正整数),则m=n.利用上面结论解决下面的问题:
(1)若3x·9x·27x=312,求x的值;
(2)若x=3m+2,y=9m+3m,用含x的代数式表示y.
解:(1)原式=3x·(32)x·(33)x=3x·32x·33x=36x.
∵36x=312,∴6x=12,
解得x=2.
(2)∵x=3m+2,∴3m=x-2.
∵y=9m+3m=32m+3m=(3m)2+3m=(x-2)2+x-2=x2-3x+2,
∴y=x2-3x+2.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
