北师大版七年级数学下册第二章相交线与平行线阶段复习习题课件(共30张PPT)
文档属性
| 名称 | 北师大版七年级数学下册第二章相交线与平行线阶段复习习题课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 368.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-14 22:47:25 | ||
图片预览


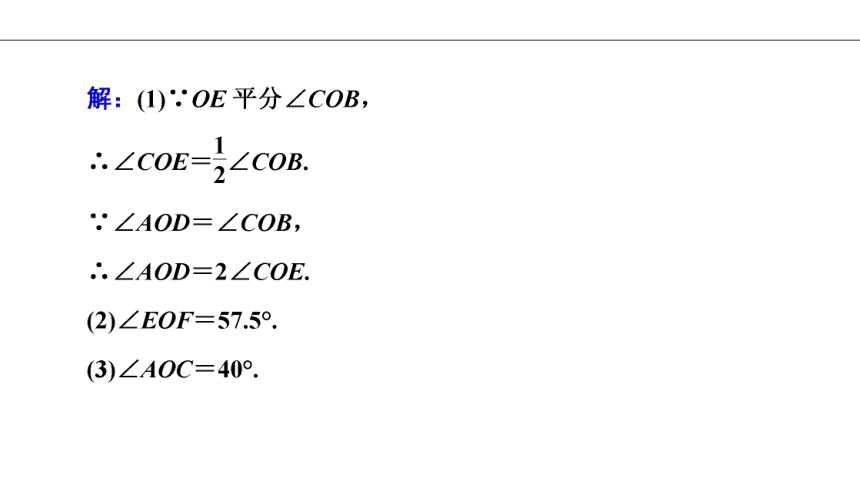




文档简介
第二章 相交线与平行线
阶段复习——直线的相交与平行
知识点1 直线的相交
例1 (2020年苏州姑苏区期末)如图,直线AB,CD交于点O,OE平分∠COB,OF是∠EOD的平分线.
(1)说明:∠AOD=2∠COE;
(2)若∠AOC=50°,求∠EOF的度数;
(3)若∠BOF=15°,求∠AOC的度数.
1.(2020年北京东城区期末)如图,O是直线AB上的一点,∠COD=90°,OC平分∠AOE,∠BOD=30°,求∠DOE的度数.
?解:∵∠BOD=30°,∠COD=90°,
∴∠AOC=90°-∠BOD=60°.
∵OC平分∠AOE,
∴∠COE=∠AOC=60°.
∴∠DOE=∠COD-∠COE=30°.
知识点2 识别同位角、内错角、同旁内角
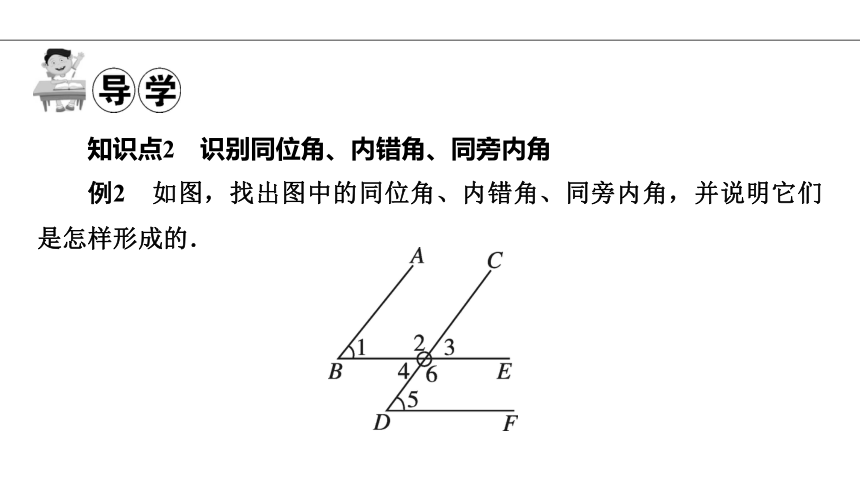
例2 如图,找出图中的同位角、内错角、同旁内角,并说明它们是怎样形成的.
解:同位角为∠1与∠3,∠3与∠5.其中∠1与∠3是直线AB,CD被直线BE所截得到的,∠3与∠5是直线BE,DF被直线CD所截得到的;
内错角为∠1与∠4,∠4与∠5.其中∠1与∠4是直线AB,CD被直线BE所截得到的,∠4与∠5是直线BE,DF被直线CD所截得到的;
同旁内角为∠1与∠2,∠6与∠5.其中∠1与∠2是直线AB,CD被直线BE所截得到的,∠6与∠5是直线BE,DF被直线CD所截得到的.
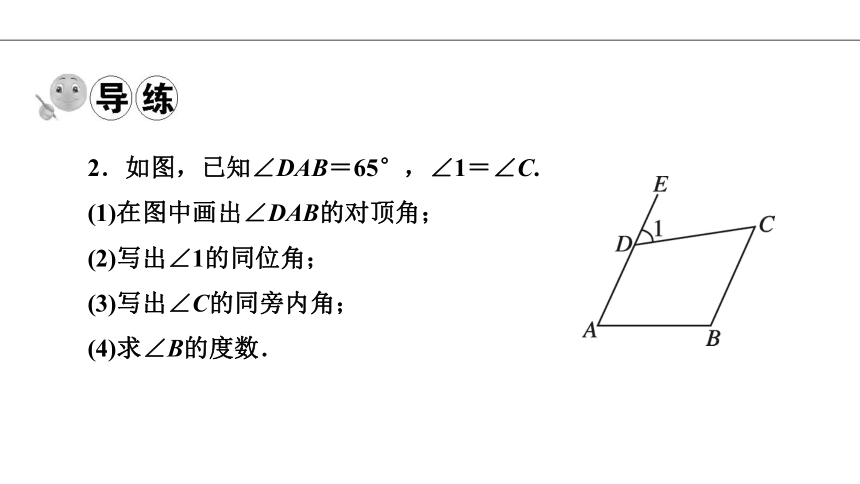
2.如图,已知∠DAB=65°,∠1=∠C.
(1)在图中画出∠DAB的对顶角;
(2)写出∠1的同位角;
(3)写出∠C的同旁内角;
(4)求∠B的度数.
解:如图,∠GAH即为所求.
(2)∠1的同位角是∠DAB.
(3)∠C的同旁内角是∠B和∠ADC.
(4)∵∠1=∠C,∴AE∥BC.
∴∠DAB+∠B=180°.
又∵∠DAB=65°,∴∠B=115°.
知识点3 平行线的判定
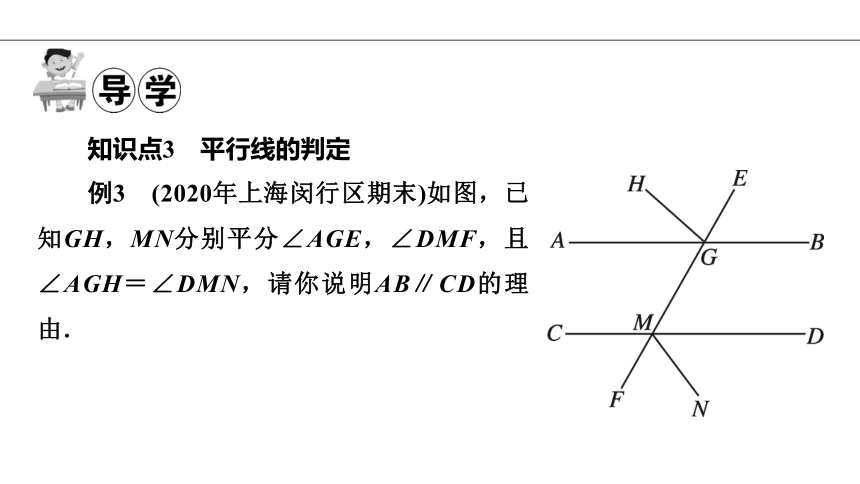
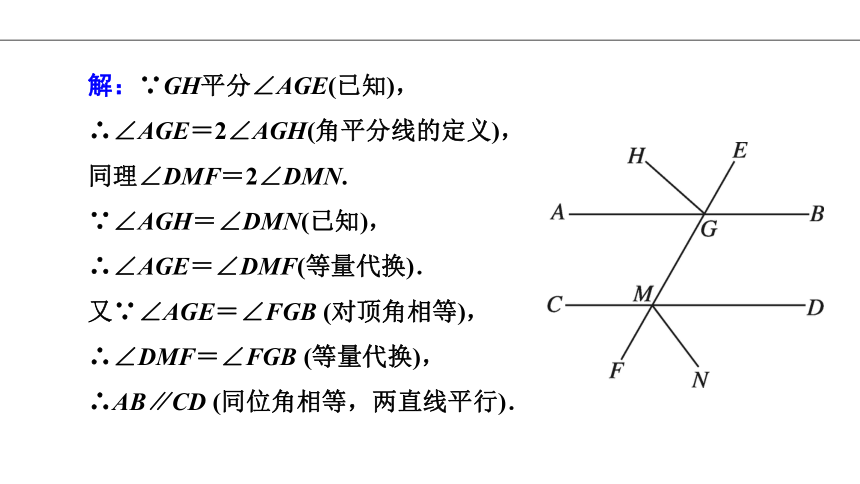
例3 (2020年上海闵行区期末)如图,已知GH,MN分别平分∠AGE,∠DMF,且∠AGH=∠DMN,请你说明AB∥CD的理由.
解:∵GH平分∠AGE(已知),
∴∠AGE=2∠AGH(角平分线的定义),
同理∠DMF=2∠DMN.
∵∠AGH=∠DMN(已知),
∴∠AGE=∠DMF(等量代换).
又∵∠AGE=∠FGB (对顶角相等),
∴∠DMF=∠FGB (等量代换),
∴AB∥CD (同位角相等,两直线平行).
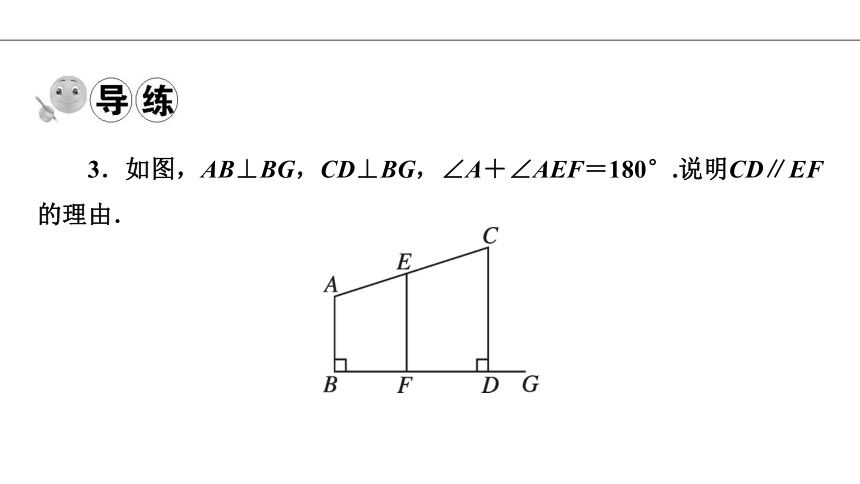
3.如图,AB⊥BG,CD⊥BG,∠A+∠AEF=180°.说明CD∥EF的理由.
?
解:∵ AB⊥BG,CD⊥BG,
∴∠B=90°,∠CDG=90°.
∴∠B=∠CDG,
∴AB∥CD(同位角相等,两直线平行).
∵∠A+∠AEF=180°,
∴AB∥EF(同旁内角互补,两直线平行).
∴ CD∥EF(平行线的传递性).
知识点4 平行线的性质
例4 如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,求:
(1)∠B的度数;
(2)∠AED的度数.
解:(1)∵AB∥CD,
∴∠B+∠C=180°.
∵∠C=120°,
∴∠B=180°-∠C=180°-120°=60°.
(2)如图,过点A作AF∥BC.
∴∠BAF=180°-∠B=180°-60°=120°.
∵∠BAE=20°,
∴∠EAF=∠BAF-∠BAE=120°-20°=100°.
∵BC∥DE,∴AF∥DE.
∴∠AED=180°-∠EAF=180°-100°=80°.
4.如图,∠ABD和∠BDC的平分线交于点E,BE交CD于点F,∠1+∠2=90°.
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFD的度数.
解:∵∠ABD和∠BDC的平分线交于点E,
∴∠ABD=2∠1,∠BDC=2∠2.
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°.
∴AB∥CD.
(2)∵∠2=25°,
∴∠1=90°-∠2=90°-25°=65°.
∵BF平分∠ABD,
∴∠ABF=∠1=65°.
∵AB∥CD,
∴∠BFD=∠ABF=65°.
?
方法点拨:本题(2)求解的技巧是做辅助线“过点A作AF∥BC”,由此构造出满足平行线性质的基本图形,需要注意的是,本题的这种方法,也是解决这类问题的常用方法.
【第一关】
1.(2020年普宁期末)下列说法错误的是 ( )
A.对顶角一定相等
B.在同一平面内,有且只有一条直线和已知直线垂直
C.同位角相等,两直线平行
D.如果两个角的和是90°,那么称这两个角互为余角
B
2.(2020年肇庆期末)如图,下列不能判断AD∥BC的是 ( )
A.∠2=∠3
B.∠1=∠4
C.∠ADC+∠C=180°
D.∠A+∠ABC=180°
B
3.(2020年北京东城区校级期末)已知∠1与∠2互余,∠3与∠4互余,如果∠1=∠3,则∠2________∠4(填“>”“=”或“<”).
4.(2020年北京顺义区期末)如图,与∠1是同旁内角的是_______,与∠1是内错角的是_______.
=
∠5
∠4
5.(2020年北京海淀区校级期末)如图,∠A=∠CEF,∠1=∠B.求证:DE∥BC.
解:∵∠A=∠CEF,∴EF∥AB,
∴∠EFC=∠B.∵∠1=∠B,
∴∠EFC=∠1,∴DE∥BC.
【第二关】
6.(2020年福州期末)如图,在三角形ABC中,若∠ACB=90°,CD⊥AB于点D,则下列线段的长度可以表示为点A到直线CD距离的是 ( )
A.AD B.AC
C.AB D.CD
A
7.在同一平面内有三条直线,如果使其中有且只有两条直线平行,那么这三条直线有且只有______个交点.
2
8.(2020年卫辉期末)如图,将一张长方形纸片ABCD沿AE折叠,若∠BAD′=26°,求∠AED′的度数.
9.(2020年重庆南岸区期末)如图,AC平分∠MAE,AE交DB于点F.
(1)若AB∥CE,∠BAE=50°,求∠ACE的度数;
(2)若∠AFB=∠CAM,说明∠ACE=∠BDE的理由.
解:(1)∵AC平分∠MAE,∴∠MAC=∠EAC.
∵∠BAE=50°,∴∠MAC=∠EAC=65°.
∵AB∥CE,∴∠ACE=∠MAC=65°.
(2)∵∠AFB=∠CAM,∴∠AFB=∠EAC.
∴AC∥BD.∴∠ACE=∠BDE.
【第三关】
10.如图是一种躺椅及其简化结构示意图,扶手AB与底座CD都平行于地面,靠背DM与支架OE平行,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,当∠EOF=90°,∠ODC=30°时,人躺着最舒服,求此时扶手AB与支架OE的夹角∠AOE和扶手AB与靠背DM的夹角∠ANM的度数.
解:∵扶手AB与底座CD都平行于地面,
∴AB∥CD.
∴∠ODC=∠BOD=30°.
又∵∠EOF=90°,
∴∠AOE=60°.
∵DM∥OE,
∴∠AND=∠AOE=60°,
∴∠ANM=180°-∠AND=120°.
阶段复习——直线的相交与平行
知识点1 直线的相交
例1 (2020年苏州姑苏区期末)如图,直线AB,CD交于点O,OE平分∠COB,OF是∠EOD的平分线.
(1)说明:∠AOD=2∠COE;
(2)若∠AOC=50°,求∠EOF的度数;
(3)若∠BOF=15°,求∠AOC的度数.
1.(2020年北京东城区期末)如图,O是直线AB上的一点,∠COD=90°,OC平分∠AOE,∠BOD=30°,求∠DOE的度数.
?解:∵∠BOD=30°,∠COD=90°,
∴∠AOC=90°-∠BOD=60°.
∵OC平分∠AOE,
∴∠COE=∠AOC=60°.
∴∠DOE=∠COD-∠COE=30°.
知识点2 识别同位角、内错角、同旁内角
例2 如图,找出图中的同位角、内错角、同旁内角,并说明它们是怎样形成的.
解:同位角为∠1与∠3,∠3与∠5.其中∠1与∠3是直线AB,CD被直线BE所截得到的,∠3与∠5是直线BE,DF被直线CD所截得到的;
内错角为∠1与∠4,∠4与∠5.其中∠1与∠4是直线AB,CD被直线BE所截得到的,∠4与∠5是直线BE,DF被直线CD所截得到的;
同旁内角为∠1与∠2,∠6与∠5.其中∠1与∠2是直线AB,CD被直线BE所截得到的,∠6与∠5是直线BE,DF被直线CD所截得到的.
2.如图,已知∠DAB=65°,∠1=∠C.
(1)在图中画出∠DAB的对顶角;
(2)写出∠1的同位角;
(3)写出∠C的同旁内角;
(4)求∠B的度数.
解:如图,∠GAH即为所求.
(2)∠1的同位角是∠DAB.
(3)∠C的同旁内角是∠B和∠ADC.
(4)∵∠1=∠C,∴AE∥BC.
∴∠DAB+∠B=180°.
又∵∠DAB=65°,∴∠B=115°.
知识点3 平行线的判定
例3 (2020年上海闵行区期末)如图,已知GH,MN分别平分∠AGE,∠DMF,且∠AGH=∠DMN,请你说明AB∥CD的理由.
解:∵GH平分∠AGE(已知),
∴∠AGE=2∠AGH(角平分线的定义),
同理∠DMF=2∠DMN.
∵∠AGH=∠DMN(已知),
∴∠AGE=∠DMF(等量代换).
又∵∠AGE=∠FGB (对顶角相等),
∴∠DMF=∠FGB (等量代换),
∴AB∥CD (同位角相等,两直线平行).
3.如图,AB⊥BG,CD⊥BG,∠A+∠AEF=180°.说明CD∥EF的理由.
?
解:∵ AB⊥BG,CD⊥BG,
∴∠B=90°,∠CDG=90°.
∴∠B=∠CDG,
∴AB∥CD(同位角相等,两直线平行).
∵∠A+∠AEF=180°,
∴AB∥EF(同旁内角互补,两直线平行).
∴ CD∥EF(平行线的传递性).
知识点4 平行线的性质
例4 如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,求:
(1)∠B的度数;
(2)∠AED的度数.
解:(1)∵AB∥CD,
∴∠B+∠C=180°.
∵∠C=120°,
∴∠B=180°-∠C=180°-120°=60°.
(2)如图,过点A作AF∥BC.
∴∠BAF=180°-∠B=180°-60°=120°.
∵∠BAE=20°,
∴∠EAF=∠BAF-∠BAE=120°-20°=100°.
∵BC∥DE,∴AF∥DE.
∴∠AED=180°-∠EAF=180°-100°=80°.
4.如图,∠ABD和∠BDC的平分线交于点E,BE交CD于点F,∠1+∠2=90°.
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFD的度数.
解:∵∠ABD和∠BDC的平分线交于点E,
∴∠ABD=2∠1,∠BDC=2∠2.
∵∠1+∠2=90°,
∴∠ABD+∠BDC=180°.
∴AB∥CD.
(2)∵∠2=25°,
∴∠1=90°-∠2=90°-25°=65°.
∵BF平分∠ABD,
∴∠ABF=∠1=65°.
∵AB∥CD,
∴∠BFD=∠ABF=65°.
?
方法点拨:本题(2)求解的技巧是做辅助线“过点A作AF∥BC”,由此构造出满足平行线性质的基本图形,需要注意的是,本题的这种方法,也是解决这类问题的常用方法.
【第一关】
1.(2020年普宁期末)下列说法错误的是 ( )
A.对顶角一定相等
B.在同一平面内,有且只有一条直线和已知直线垂直
C.同位角相等,两直线平行
D.如果两个角的和是90°,那么称这两个角互为余角
B
2.(2020年肇庆期末)如图,下列不能判断AD∥BC的是 ( )
A.∠2=∠3
B.∠1=∠4
C.∠ADC+∠C=180°
D.∠A+∠ABC=180°
B
3.(2020年北京东城区校级期末)已知∠1与∠2互余,∠3与∠4互余,如果∠1=∠3,则∠2________∠4(填“>”“=”或“<”).
4.(2020年北京顺义区期末)如图,与∠1是同旁内角的是_______,与∠1是内错角的是_______.
=
∠5
∠4
5.(2020年北京海淀区校级期末)如图,∠A=∠CEF,∠1=∠B.求证:DE∥BC.
解:∵∠A=∠CEF,∴EF∥AB,
∴∠EFC=∠B.∵∠1=∠B,
∴∠EFC=∠1,∴DE∥BC.
【第二关】
6.(2020年福州期末)如图,在三角形ABC中,若∠ACB=90°,CD⊥AB于点D,则下列线段的长度可以表示为点A到直线CD距离的是 ( )
A.AD B.AC
C.AB D.CD
A
7.在同一平面内有三条直线,如果使其中有且只有两条直线平行,那么这三条直线有且只有______个交点.
2
8.(2020年卫辉期末)如图,将一张长方形纸片ABCD沿AE折叠,若∠BAD′=26°,求∠AED′的度数.
9.(2020年重庆南岸区期末)如图,AC平分∠MAE,AE交DB于点F.
(1)若AB∥CE,∠BAE=50°,求∠ACE的度数;
(2)若∠AFB=∠CAM,说明∠ACE=∠BDE的理由.
解:(1)∵AC平分∠MAE,∴∠MAC=∠EAC.
∵∠BAE=50°,∴∠MAC=∠EAC=65°.
∵AB∥CE,∴∠ACE=∠MAC=65°.
(2)∵∠AFB=∠CAM,∴∠AFB=∠EAC.
∴AC∥BD.∴∠ACE=∠BDE.
【第三关】
10.如图是一种躺椅及其简化结构示意图,扶手AB与底座CD都平行于地面,靠背DM与支架OE平行,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,当∠EOF=90°,∠ODC=30°时,人躺着最舒服,求此时扶手AB与支架OE的夹角∠AOE和扶手AB与靠背DM的夹角∠ANM的度数.
解:∵扶手AB与底座CD都平行于地面,
∴AB∥CD.
∴∠ODC=∠BOD=30°.
又∵∠EOF=90°,
∴∠AOE=60°.
∵DM∥OE,
∴∠AND=∠AOE=60°,
∴∠ANM=180°-∠AND=120°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
