2020-2021学年北师大版小学六年级数学下册《第三单元 图形的运动》单元测试题(解析版)
文档属性
| 名称 | 2020-2021学年北师大版小学六年级数学下册《第三单元 图形的运动》单元测试题(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 397.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-14 21:22:04 | ||
图片预览


文档简介
2020-2021学年北师大版小学六年级数学下册《第三单元
图形的运动》单元测试题
一.选择题(共8小题)
1.如图,将三角形A绕点O( ),可以得到三角形B.
A.按逆时针方向旋转90°
B.按顺时针方向旋转60°
C.按顺时针方向旋转90°
2.下列4个图形中,有( )几个图形旋转180度后和原来的图形是一样的.
A.1个
B.2个
C.3个
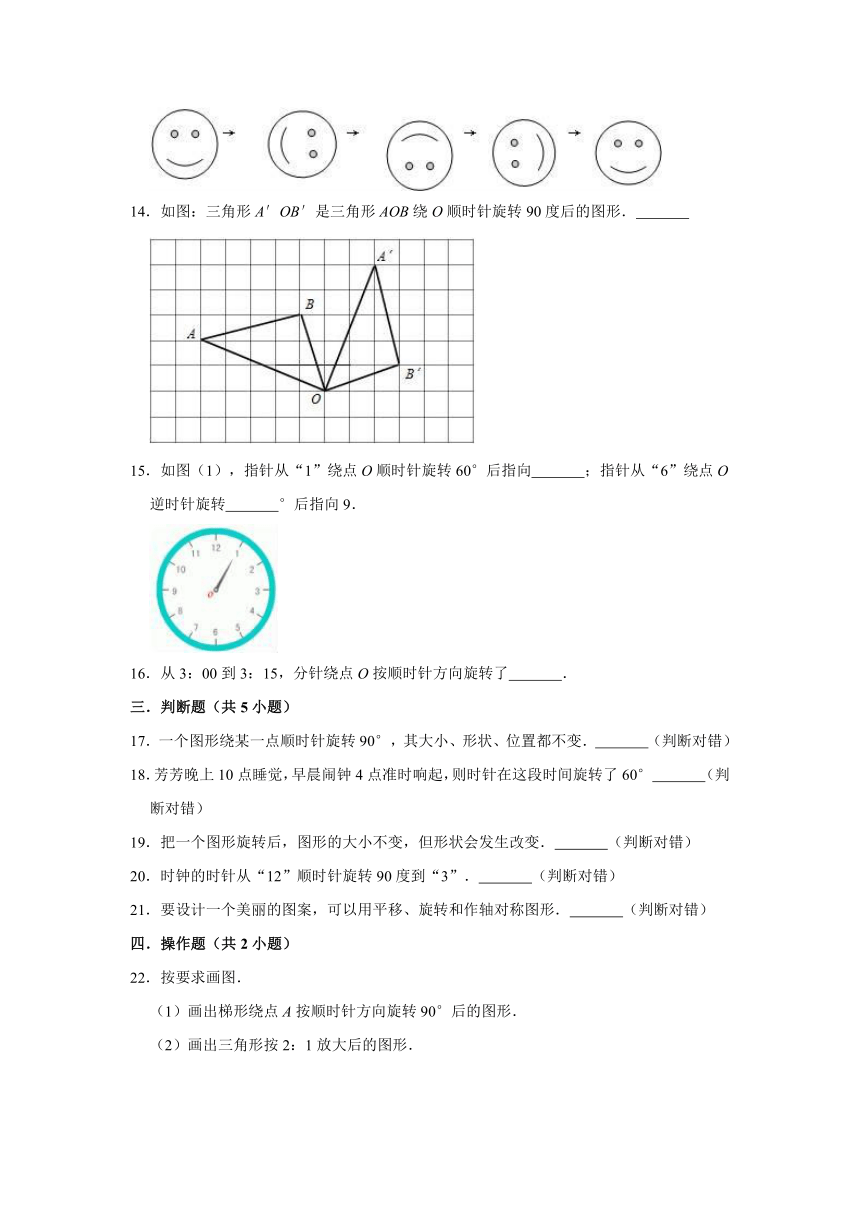
D.4个
3.将逆时针旋转90度得到的图形是( )
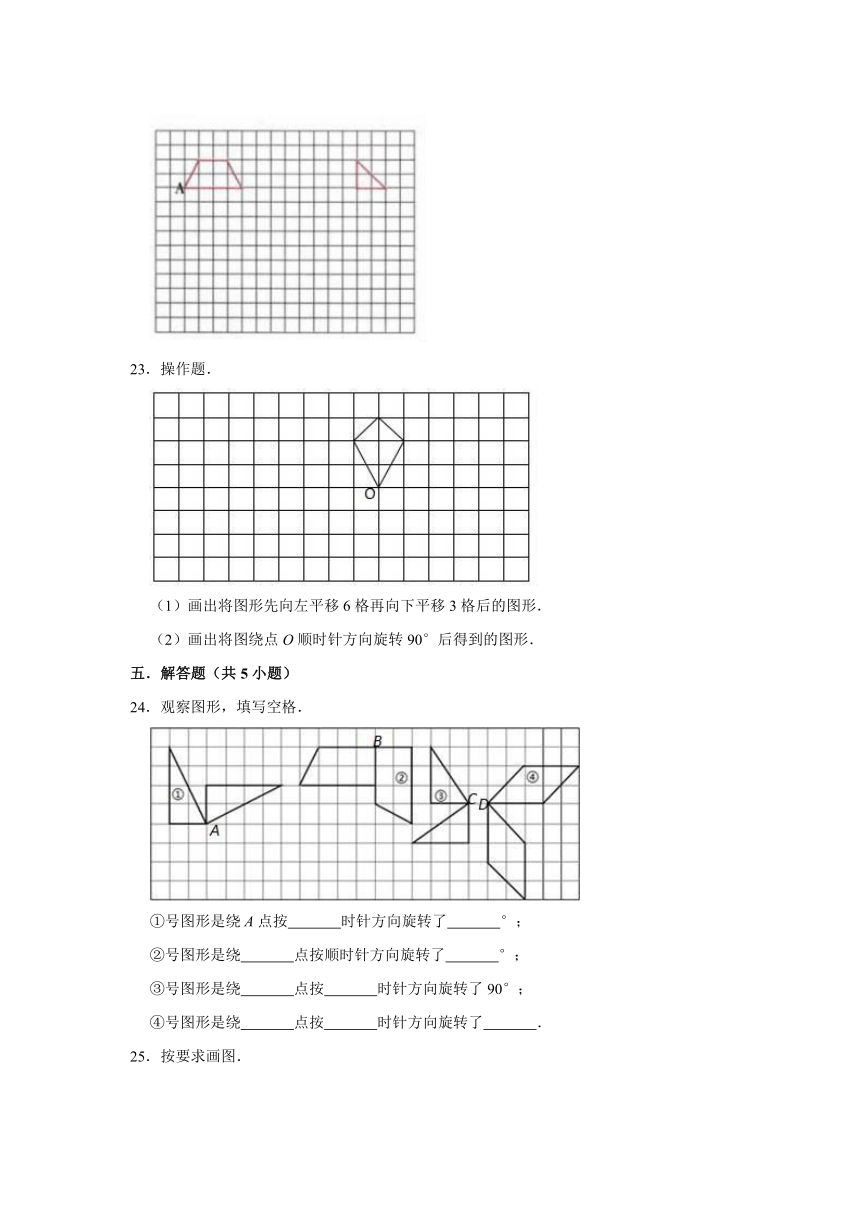
A.
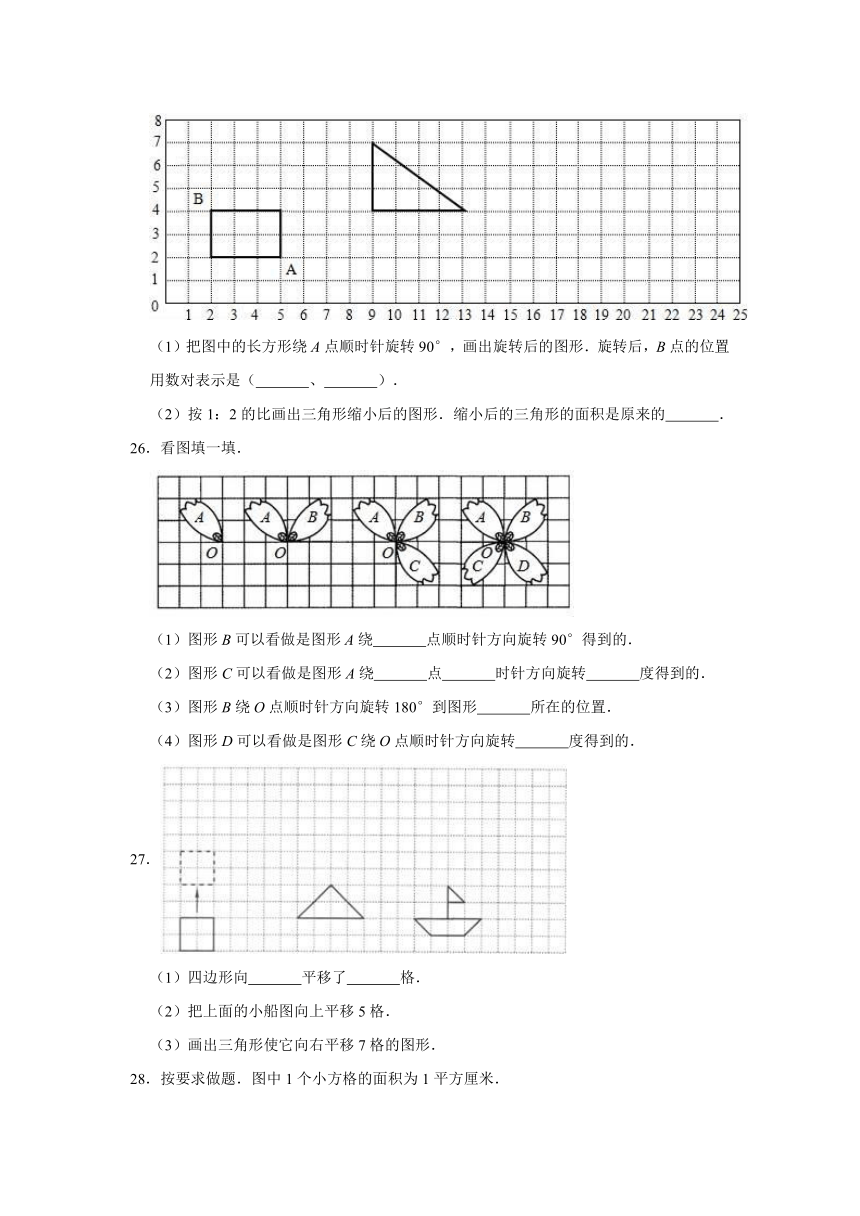
B.
C.
4.将图形按顺时针方向旋转90°后的图形是( )
A.
B.
C.
D.
5.把正方形的右边剪去一块补到上面(如图),得到的图形是( )
A.
B.
C.
D.
6.下面每组中的两个图形经过平移后,可以互相重合的是( )
A.
B.
C.
D.
7.下面的图案可以通过平移得到的是( )
A.
B.
C.
8.钟面上时针从6逆时针旋转90°后,应该指着( )
A.3
B.9
C.12
二.填空题(共8小题)
9.汽车在笔直的公路上行驶,车身的运动是
现象.
10.如图中,以直线为轴旋转,可以得出圆柱体的是
,得出圆锥体的是
A.
B.
C.
D.
11.如图是一个直角三角形(单位:厘米)
(1)以三角形较长的直角边为轴旋转一周,形成的图形是
,这个图形的体积是
立方厘米.
(2)以三角形较短的直角边为轴旋转一周,形成的图形是
,这个图形的体积是
立方厘米.
12.生活中利用图形的
、
和
来对图形进行变换设计.
13.如图所示,小笑脸按
时针方向旋转,每次旋转
度.
14.如图:三角形A′OB′是三角形AOB绕O顺时针旋转90度后的图形.
15.如图(1),指针从“1”绕点O顺时针旋转60°后指向
;指针从“6”绕点O逆时针旋转
°后指向9.
16.从3:00到3:15,分针绕点O按顺时针方向旋转了
.
三.判断题(共5小题)
17.一个图形绕某一点顺时针旋转90°,其大小、形状、位置都不变.
(判断对错)
18.芳芳晚上10点睡觉,早晨闹钟4点准时响起,则时针在这段时间旋转了60°
(判断对错)
19.把一个图形旋转后,图形的大小不变,但形状会发生改变.
(判断对错)
20.时钟的时针从“12”顺时针旋转90度到“3”.
(判断对错)
21.要设计一个美丽的图案,可以用平移、旋转和作轴对称图形.
(判断对错)
四.操作题(共2小题)
22.按要求画图.
(1)画出梯形绕点A按顺时针方向旋转90°后的图形.
(2)画出三角形按2:1放大后的图形.
23.操作题.
(1)画出将图形先向左平移6格再向下平移3格后的图形.
(2)画出将图绕点O顺时针方向旋转90°后得到的图形.
五.解答题(共5小题)
24.观察图形,填写空格.
①号图形是绕A点按
时针方向旋转了
°;
②号图形是绕
点按顺时针方向旋转了
°;
③号图形是绕
点按
时针方向旋转了90°;
④号图形是绕
点按
时针方向旋转了
.
25.按要求画图.
(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形.旋转后,B点的位置用数对表示是(
、
).
(2)按1:2的比画出三角形缩小后的图形.缩小后的三角形的面积是原来的
.
26.看图填一填.
(1)图形B可以看做是图形A绕
点顺时针方向旋转90°得到的.
(2)图形C可以看做是图形A绕
点
时针方向旋转
度得到的.
(3)图形B绕O点顺时针方向旋转180°到图形
所在的位置.
(4)图形D可以看做是图形C绕O点顺时针方向旋转
度得到的.
27.
(1)四边形向
平移了
格.
(2)把上面的小船图向上平移5格.
(3)画出三角形使它向右平移7格的图形.
28.按要求做题.图中1个小方格的面积为1平方厘米.
(1)把三角形绕点B逆时针旋转90o,画出旋转后的图形.
(2)标出点D(2,2)和点E(6,2)的位置.
(3)以DE为下底,画一个上底为2厘米,高为3厘米的等腰梯形.
(4)画出的梯形的面积是
平方厘米.
参考答案与试题解析
一.选择题(共8小题)
1.【分析】根据旋转的特征,图形A绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,即可到达图形B的位置.
【解答】解:如图,
将三角形A绕点O按顺时针方向旋转90°,可以得到三角形B.
故选:C.
【点评】经过旋转,图形上的每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.(旋转前后两个图形的对应线段相等、对应角相等).关键是看对应线段之间的夹角是多少度.
2.【分析】图1可以看作由一部分绕中心旋转5个60°,或由一部分绕中心旋转2个60°,再旋转180°而成;图2由4个图案组成,这4个图案可分为左、右两部分或上、下两部分,因此,可看作是由一部分旋转180°而成;图2是由一部分经过平移后而得到的,上、下为轴对称图形,因此,旋转180°后也能与原来的图形重合;图4可看作是由中间一个小圆,外边一个较大圆绕小圆圆心旋转4个70°而成,旋转180°不会与原图重合.
【解答】解:根据旋转的特征,图1、图2和图3旋转180°后都能和原来的图形重合,即旋转180°后与原来的图形一样,图形4则不能.
故选:C.
【点评】此题是考查作旋转一定度数后的图形,根据各图形的特征及旋转的特征即可判定.
3.【分析】观察图形,箭头原来指向上,逆时针旋转90度后,箭头应该指向左,据此即可选择.
【解答】解:根据题干分析可得,将逆时针旋转90度得到的图形是.
故选:A.
【点评】此题考查了图形的旋转方法的灵活应用.
4.【分析】根据旋转的性质,图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动,其中对应点到旋转中心的距离相等,旋转前后图形的大小和形状没有改变;图片按顺时针方向旋转90°,分析可得答案.
【解答】解:根据旋转的意义,图片按顺时针方向旋转90°,分析可得D符合.
故选:D.
【点评】本题考查了图形的旋转变化,要看清是顺时针还是逆时针旋转,旋转多少度,难度不大,但易错.
5.【分析】把正方形的右边剪去一块,正方形缺失是右边,据此排除答案A和C.又因为剪去的部分是补到上面,答案D补到了下面,排除D,所以选B.
【解答】解:把正方形的右边剪去一块补到上面,只有C符合题意.
故选:B.
【点评】解答此题最好的办法是动手操作一下,即可以解决问题,又锻炼动手操作能力.
6.【分析】平移后可以重合的两个图形,必须是完全一样,方向一致据此可解答.
【解答】解:下面每组中的两个图形经过平移后,可以互相重合的是;
故选:C.
【点评】本题考查了对平移后图形与平移前图形的比较.
7.【分析】平移:把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。平移后图形的位置改变,形状、大小、方向不变。
【解答】解:平移是物体运动时,物体任意两点间,从一点到另一点的方向的距离都不变的的运动;结合图形可知:A图形可以通过平移得到。
故选:A。
【点评】本题主要考查平移的意义,明确平移的意义,是解答此题的关键。
8.【分析】钟面上有12个数字,这12个数字把一个周角平均分成了12份,一个周角是360°,每份是360°÷12=30°,即两个相邻数字间的度数是30°,时针从“6”绕中心点O逆时针旋转90°,90°÷30°=3,就是旋转了3个数字,6﹣3=3,此时时针指向“3”,
【解答】解:时针从“6”绕中心点O逆时针旋转90°,90°÷30°=3,就是旋转了3个数字,6﹣3=3,此时时针指向“3”;
故选:A.
【点评】解答本题主要掌握钟面上的12个数字把一个周角平均分成了12份,每份是360°÷12=30°,即个相邻数字间的度数是30°.
二.填空题(共8小题)
9.【分析】平移是物体运动时,物体上任意两点间,从一点到另一点的方向与距离都不变的运动;
旋转是物体运动时,每一个点离同一个点(可以在物体外)的距离不变的运动,称为绕这个点的转动,这个点称为物体的转动中心.所以,它并不一定是绕某个轴的.
根据平移与旋转定义判断即可.
【解答】解:汽车在笔直的公路上行驶,车身的运动是平移现象.
故答案为:平移.
【点评】平移与旋转的区别在于看方向是否发生改变,平移不改变图形方向,旋转改变图形方向.
10.【分析】根据点动成线,线动成面,面动成体.以长方形或正方形的一边为轴,旋转一周,长方形或正方形的另外两个顶点绕轴旋转构成两个等圆,这两个圆面是圆柱的两个底,与轴平行的一边构成一个曲面,这就是圆柱的侧面,就是说正方形或长方形绕一边旋转一周会得到一个圆柱;同理以直角三角形角边为轴旋转一周会得到一个以旋转轴变高,另一直角边为底面半径的圆锥.
【解答】解:如图中,以直线为轴旋转,可以得出圆柱体的是长方形或正方形,得出圆锥体的是直角三角形.
故选:B,C.
【点评】此题主要考查立体图形中旋转体,也就是把一个图形绕一条直线旋转得到的图形,要基本的图形特征,才能正确判定.
11.【分析】(1)以三角形较长的直角边为轴旋转一周,形成的图形是高为4厘米底面半径为3厘米的圆锥,根据圆锥的体积公式“V=πr2h”即可求出它的体积.
(2)以三角形较短的直角边为轴旋转一周,形成的图形是高为3厘米底面半径为4厘米的圆锥,根据圆锥的体积公式“V=πr2h”即可求出它的体积.
【解答】解:(1)×3.14×32×4
=×3.14×9×4
=37.68(立方厘米)
答:以三角形较长的直角边为轴旋转一周,形成的图形是高为4厘米底面半径为3厘米的圆锥,这个图形的体积是37.68立方厘米.
(2)×3.14×42×3
=×3.14×16×3
=50.24(立方厘米)
答:以三角形较短的直角边为轴旋转一周,形成的图形是高为3厘米底面半径为4厘米的圆锥,这个图形的体积是50.24立方厘米.
故答案为:高为4厘米底面半径为3厘米的圆锥,37.68;高为3厘米底面半径为4厘米的圆锥,50.24.
【点评】以直角三形一直角边为轴旋转一周可形成以旋转轴为高另一直角边为底面半径的圆锥;求圆锥的体积关键记住公式.
12.【分析】生活中经常先设计一个单一图形或图形的一部分,通过平移、旋转即可形成一幅完整的图案,或设计一个图案的一半,能轴对称画出它的另一半.
【解答】解:生活中利用图形的平移、旋转和轴对称来对图形进行变换设计.
故答案为:平移、旋转、轴对称.
【点评】利用图形的平移、旋转、轴对称,设计图案是常用的方法.
13.【分析】根据旋转的意义,找出图中相邻两个笑脸的眼睛和嘴巴,两个关键处是沿什么方向旋转的,然后再确定旋转的度数即可.
【解答】解:如图所示,小笑脸按
顺时针方向旋转,每次旋转
90度.
故答案为:顺,90.
【点评】本题考查的是图形旋转的变化,解答时关键理清是顺时针还是逆时针旋转,然后再找出旋转度数即可.
14.【分析】因为上图在旋转时,O点保持不动,将底边OA向上移动了,因此三角形A′OB′是三角形AOB绕O点顺时针旋转90度后的图形.
【解答】解:由以上分析:
上图三角形A′OB′是三角形AOB绕O顺时针旋转90度后的图形.
故答案为:√.
【点评】掌握旋转以及顺时针、逆时针的概念,是解答此题的关键.
15.【分析】
根据图示可得,每个大格对应的度数是30°,用60除以30可得指针从“1”绕点O顺时针旋转60°的格子数,进一步可得对着数字几;数出指针从“6”绕点O逆时针旋转到“9”的格子数,然后再乘30即可.
【解答】解:如图所示:
60÷30=2(个)
1+2=3
即,指针从“1”绕点O顺时针旋转60°后指向“3”;
30×9=270(度)
即,指针从“6”绕点O逆时针旋转
270°后指向9.
故答案为:“3”,270.
【点评】本题考查了图形的旋转变化,学生主要看清是顺时针还是逆时针旋转,旋转多少度,和旋转的格子数.
16.【分析】钟面上12个数字把钟面平均分成12份,每份所对应的圆心角是360°÷12=30°,每两个相邻数字间的夹角是30°,即指针从一个数字走到下一个数字时,绕中心轴旋转了30°.3:00分针指向12,3:15分针指向3,分针绕点O按顺时针方向旋转了3个30°,即90°
【解答】解:从3:00到3:15,分针绕点O按顺时针方向旋转了90°.
故答案为:90°.
【点评】关键明白,在钟面上,指针从一个数字旋转到另一个数字,旋转了30°.
三.判断题(共5小题)
17.【分析】根据旋转的特征,一个图形绕某点顺时针旋转90°,某点的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形,即旋转后形状、大小不变,只是位置发生变化.
【解答】解:一个图形绕某一点顺时针旋转90°,其大小、形状不变,位置发生变化,原题的说法是错误的.
故答案为:×.
【点评】此题是考查旋转的特征.图形平移、旋转后形状、大小不变,只是位置发生变化.
18.【分析】钟面上12个数字把钟面平均分成12份,每份所对应的圆心角是360°÷12=30°,即每两个相邻数字间的夹角是30°,即指针从一个数字走到下一个数字时,绕中心轴旋转了30°,从晚上10点到早晨闹钟4点,时针从数字10走到数字12,再走到数字4,走了(12﹣10)+4=6(个)数字,30°×6=180°.
【解答】解:(12﹣10)+4=6
30°×6=180°.
即芳芳晚上10点睡觉,早晨闹钟4点准时响起,则时针在这段时间旋转了180°.
故答案为:×.
【点评】此题是考查钟表的认识与时间的推算.关键明白即指针从一个数字走到下一个数字时绕中心轴旋转多少度,这期间走了几个数字.
19.【分析】旋转:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫作图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。
据此解答即可。
【解答】解:把一个图形旋转后,图形的形状、大小不变。
故原题说法错误。
故答案为:×。
【点评】此题考查了旋转的意义及在实际当中的运用。
20.【分析】钟面上12个数字,以表芯为旋转点,表针转一圈是360°,被12个数字平均分成12份,每一份也就是两数之间夹角是30°;时钟的时针从“12”顺时针旋转30×3=90度到“3”,据此解答即可。
【解答】解:时钟的时针从“12”顺时针旋转90度到“3”,说法正确。
故答案为:√。
【点评】此题考查了旋转的意义及在实际当中的运用。
21.【分析】通常对一个简单的图案通过平移、旋转、或者做轴对称图形的方法,产生多个相似的图形,从而变成一个美丽的图案.
【解答】解:可以用平移、旋转和作轴对称图形等方法,设计出美丽的图案.
故答案为:√.
【点评】利用平移、旋转、对称设计图形,都要选准基本图案.平移定好平移的格数;对称定好对称轴,选好对称点;旋转选好旋转点,依次沿每次旋转后的基本图的边缘旋转图案.
四.操作题(共2小题)
22.【分析】(1)根据旋转的意义,找出图中梯形的4个关键处,再画出绕A点按顺时针方向旋转90度后的形状即可.
(2)按2:1的比例画出梯形放大后的图形,就是把原三角形的底和高分别扩大到原来的2倍,原三角形的底和高分别是2格和2格,扩大后的三角形的底和高分别是4格和4格.
【解答】解:(1)梯形绕点A按顺时针方向旋转90°后的图形
(2)三角形按2:1放大后的图形
如图所示:
【点评】本题考查了图形的旋转和放大与缩小变化,学生主要看清是顺时针还是逆时针旋转,旋转多少度,以及放大或缩小的倍数.
23.【分析】(1)根据平移的特征,把此图的各顶点先分别向左平移6格,再向下平移3格,依次连结即可得到平移后的图形。
(2)根据旋转的特征,把此图绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
【解答】解:(1)画出将图形先向左平移6格再向下平移3格后的图形(下图红色部分)。
(2)画出将图绕点O顺时针方向旋转90°后得到的图形(下图绿色部分)。
【点评】图形平移注意三要素:即原位置、平移方向、平移距离。图形旋转注意四要素:即原位置、旋转中心、旋转方向、旋转角。
五.解答题(共5小题)
24.【分析】根据旋转的特征,一个图形绕某点按一定的方向旋转一定的度数,某占的位置不动,其余各部分均绕某点按相同的方向旋转相同的度数.据此即可得知:①号图形是绕A点按顺时针方向旋转了90°;②号图形是绕B点按顺时针方向旋转了90°;③号图形是绕C点按逆时针方向旋转了90°;④号图形是绕D点按顺时针方向旋转了90°.
【解答】解:①号图形是绕A点按顺时针方向旋转了90°;②号图形是绕B点按顺时针方向旋转了90°;
③号图形是绕C点按逆时针方向旋转了90°;
④号图形是绕D点按顺时针方向旋转了90°.
故答案为:顺,90,B,90,C,逆,D,顺,90°.
【点评】旋转作图要注意:①旋转方向;②旋转角度.整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动.
25.【分析】(1)根据旋转的特征,把长方形绕点A顺时针旋转90°后,点A的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;根据旋转后点B的位置及用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即要用数对表示出点B的位置.
(2)图中三角形是一两直角边分别为3格,4格的直角三角形,根据图形放大与缩小的意义,按1:2缩小后的三角形是一两直角边分别为1.5格,2格的直角三角形;分别求原三角形和缩小后三角形的面积,用缩小后三角形的面积除以原三角形的面积(用最简分数表示).
【解答】解:(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形(下图红色部分).旋转后,B点的位置用数对表示是(7、5).
(2)按1:2的比画出三角形缩小后的图形(下图绿色部分).
缩小后的三角形面积:1.5×2÷2=1.5
原三角形面积:3×4÷2=6
1.5÷6=
即缩小后的三角形的面积是原来的.
故答案为:7,5;.
【点评】此题考查的知识点有作旋转一定度数后的图形、点与数对、图形的放大与缩小、三角形面积的计算、分数的意义等.
26.【分析】旋转的要素是旋转方向,旋转中心,旋转角,据此即可解决问题.
【解答】解:根据观察,(1)图形B可以看作是图形A绕点O顺时针旋转90°得到的;
(2)图形C可以看做是图形A绕点O顺时针方向旋转180°所得到的;
(3)图形B绕点O顺时针旋转180°到图形D所在的位置;
(4)图形D可以看作图形C绕点O顺时针方向旋转90°得到的.
故答案为:(1)O;(2)O;顺;180;(3)D;(4)90.
【点评】本题主要考查了旋转的要素,是需要熟记的内容.
27.【分析】根据平移的特征,
(1)图(1)向上平移了4格,
(2)把图(2)中的小船图顶点分别向上平移了5格,
(3)把图(3)中的三角形顶点分别向右平移了7格.
【解答】解:(1)图(1)向上平移了4格,
(2)把图(2)中的小船图顶点分别向上平移了5格,
(3)把图(3)中的三角形顶点分别向右平移了7格.
故答案为:上,4.
【点评】本题主要考查了图形的平移,图形平移后形状、大小不变,只是位置变化.
28.【分析】(1)根据旋转的特征,三角形ABC绕点B逆时针旋转90°,点B的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形.
(2)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可标出点D(2,2)和点E(6,2)的位置.
(3)根据等腰梯形的特征,即可以DE为下底,画一个上底为2厘米,高为3厘米的等腰梯形.
(4)根据梯形的面积计算公式“S=(a+b)h”即可解答.
【解答】解:(1)把三角形绕点B逆时针旋转90o,画出旋转后的图形(三角形A′BC′).
(2)标出点D(2,2)和点E(6,2)的位置(下图).
(3)以DE为下底,画一个上底为2厘米,高为3厘米的等腰梯形(等腰梯形DEFG).
(4)画出的梯形的面积是:
(2+4)×3×
=6×3×
=9(平方厘米).
故答案为:9.
【点评】此题考查的知识有:作旋转一定度数后的图形、数对与位置,等腰梯形的意义、梯形面积的计算等.
图形的运动》单元测试题
一.选择题(共8小题)
1.如图,将三角形A绕点O( ),可以得到三角形B.
A.按逆时针方向旋转90°
B.按顺时针方向旋转60°
C.按顺时针方向旋转90°
2.下列4个图形中,有( )几个图形旋转180度后和原来的图形是一样的.
A.1个
B.2个
C.3个
D.4个
3.将逆时针旋转90度得到的图形是( )
A.
B.
C.
4.将图形按顺时针方向旋转90°后的图形是( )
A.
B.
C.
D.
5.把正方形的右边剪去一块补到上面(如图),得到的图形是( )
A.
B.
C.
D.
6.下面每组中的两个图形经过平移后,可以互相重合的是( )
A.
B.
C.
D.
7.下面的图案可以通过平移得到的是( )
A.
B.
C.
8.钟面上时针从6逆时针旋转90°后,应该指着( )
A.3
B.9
C.12
二.填空题(共8小题)
9.汽车在笔直的公路上行驶,车身的运动是
现象.
10.如图中,以直线为轴旋转,可以得出圆柱体的是
,得出圆锥体的是
A.
B.
C.
D.
11.如图是一个直角三角形(单位:厘米)
(1)以三角形较长的直角边为轴旋转一周,形成的图形是
,这个图形的体积是
立方厘米.
(2)以三角形较短的直角边为轴旋转一周,形成的图形是
,这个图形的体积是
立方厘米.
12.生活中利用图形的
、
和
来对图形进行变换设计.
13.如图所示,小笑脸按
时针方向旋转,每次旋转
度.
14.如图:三角形A′OB′是三角形AOB绕O顺时针旋转90度后的图形.
15.如图(1),指针从“1”绕点O顺时针旋转60°后指向
;指针从“6”绕点O逆时针旋转
°后指向9.
16.从3:00到3:15,分针绕点O按顺时针方向旋转了
.
三.判断题(共5小题)
17.一个图形绕某一点顺时针旋转90°,其大小、形状、位置都不变.
(判断对错)
18.芳芳晚上10点睡觉,早晨闹钟4点准时响起,则时针在这段时间旋转了60°
(判断对错)
19.把一个图形旋转后,图形的大小不变,但形状会发生改变.
(判断对错)
20.时钟的时针从“12”顺时针旋转90度到“3”.
(判断对错)
21.要设计一个美丽的图案,可以用平移、旋转和作轴对称图形.
(判断对错)
四.操作题(共2小题)
22.按要求画图.
(1)画出梯形绕点A按顺时针方向旋转90°后的图形.
(2)画出三角形按2:1放大后的图形.
23.操作题.
(1)画出将图形先向左平移6格再向下平移3格后的图形.
(2)画出将图绕点O顺时针方向旋转90°后得到的图形.
五.解答题(共5小题)
24.观察图形,填写空格.
①号图形是绕A点按
时针方向旋转了
°;
②号图形是绕
点按顺时针方向旋转了
°;
③号图形是绕
点按
时针方向旋转了90°;
④号图形是绕
点按
时针方向旋转了
.
25.按要求画图.
(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形.旋转后,B点的位置用数对表示是(
、
).
(2)按1:2的比画出三角形缩小后的图形.缩小后的三角形的面积是原来的
.
26.看图填一填.
(1)图形B可以看做是图形A绕
点顺时针方向旋转90°得到的.
(2)图形C可以看做是图形A绕
点
时针方向旋转
度得到的.
(3)图形B绕O点顺时针方向旋转180°到图形
所在的位置.
(4)图形D可以看做是图形C绕O点顺时针方向旋转
度得到的.
27.
(1)四边形向
平移了
格.
(2)把上面的小船图向上平移5格.
(3)画出三角形使它向右平移7格的图形.
28.按要求做题.图中1个小方格的面积为1平方厘米.
(1)把三角形绕点B逆时针旋转90o,画出旋转后的图形.
(2)标出点D(2,2)和点E(6,2)的位置.
(3)以DE为下底,画一个上底为2厘米,高为3厘米的等腰梯形.
(4)画出的梯形的面积是
平方厘米.
参考答案与试题解析
一.选择题(共8小题)
1.【分析】根据旋转的特征,图形A绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数,即可到达图形B的位置.
【解答】解:如图,
将三角形A绕点O按顺时针方向旋转90°,可以得到三角形B.
故选:C.
【点评】经过旋转,图形上的每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.(旋转前后两个图形的对应线段相等、对应角相等).关键是看对应线段之间的夹角是多少度.
2.【分析】图1可以看作由一部分绕中心旋转5个60°,或由一部分绕中心旋转2个60°,再旋转180°而成;图2由4个图案组成,这4个图案可分为左、右两部分或上、下两部分,因此,可看作是由一部分旋转180°而成;图2是由一部分经过平移后而得到的,上、下为轴对称图形,因此,旋转180°后也能与原来的图形重合;图4可看作是由中间一个小圆,外边一个较大圆绕小圆圆心旋转4个70°而成,旋转180°不会与原图重合.
【解答】解:根据旋转的特征,图1、图2和图3旋转180°后都能和原来的图形重合,即旋转180°后与原来的图形一样,图形4则不能.
故选:C.
【点评】此题是考查作旋转一定度数后的图形,根据各图形的特征及旋转的特征即可判定.
3.【分析】观察图形,箭头原来指向上,逆时针旋转90度后,箭头应该指向左,据此即可选择.
【解答】解:根据题干分析可得,将逆时针旋转90度得到的图形是.
故选:A.
【点评】此题考查了图形的旋转方法的灵活应用.
4.【分析】根据旋转的性质,图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动,其中对应点到旋转中心的距离相等,旋转前后图形的大小和形状没有改变;图片按顺时针方向旋转90°,分析可得答案.
【解答】解:根据旋转的意义,图片按顺时针方向旋转90°,分析可得D符合.
故选:D.
【点评】本题考查了图形的旋转变化,要看清是顺时针还是逆时针旋转,旋转多少度,难度不大,但易错.
5.【分析】把正方形的右边剪去一块,正方形缺失是右边,据此排除答案A和C.又因为剪去的部分是补到上面,答案D补到了下面,排除D,所以选B.
【解答】解:把正方形的右边剪去一块补到上面,只有C符合题意.
故选:B.
【点评】解答此题最好的办法是动手操作一下,即可以解决问题,又锻炼动手操作能力.
6.【分析】平移后可以重合的两个图形,必须是完全一样,方向一致据此可解答.
【解答】解:下面每组中的两个图形经过平移后,可以互相重合的是;
故选:C.
【点评】本题考查了对平移后图形与平移前图形的比较.
7.【分析】平移:把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移。平移后图形的位置改变,形状、大小、方向不变。
【解答】解:平移是物体运动时,物体任意两点间,从一点到另一点的方向的距离都不变的的运动;结合图形可知:A图形可以通过平移得到。
故选:A。
【点评】本题主要考查平移的意义,明确平移的意义,是解答此题的关键。
8.【分析】钟面上有12个数字,这12个数字把一个周角平均分成了12份,一个周角是360°,每份是360°÷12=30°,即两个相邻数字间的度数是30°,时针从“6”绕中心点O逆时针旋转90°,90°÷30°=3,就是旋转了3个数字,6﹣3=3,此时时针指向“3”,
【解答】解:时针从“6”绕中心点O逆时针旋转90°,90°÷30°=3,就是旋转了3个数字,6﹣3=3,此时时针指向“3”;
故选:A.
【点评】解答本题主要掌握钟面上的12个数字把一个周角平均分成了12份,每份是360°÷12=30°,即个相邻数字间的度数是30°.
二.填空题(共8小题)
9.【分析】平移是物体运动时,物体上任意两点间,从一点到另一点的方向与距离都不变的运动;
旋转是物体运动时,每一个点离同一个点(可以在物体外)的距离不变的运动,称为绕这个点的转动,这个点称为物体的转动中心.所以,它并不一定是绕某个轴的.
根据平移与旋转定义判断即可.
【解答】解:汽车在笔直的公路上行驶,车身的运动是平移现象.
故答案为:平移.
【点评】平移与旋转的区别在于看方向是否发生改变,平移不改变图形方向,旋转改变图形方向.
10.【分析】根据点动成线,线动成面,面动成体.以长方形或正方形的一边为轴,旋转一周,长方形或正方形的另外两个顶点绕轴旋转构成两个等圆,这两个圆面是圆柱的两个底,与轴平行的一边构成一个曲面,这就是圆柱的侧面,就是说正方形或长方形绕一边旋转一周会得到一个圆柱;同理以直角三角形角边为轴旋转一周会得到一个以旋转轴变高,另一直角边为底面半径的圆锥.
【解答】解:如图中,以直线为轴旋转,可以得出圆柱体的是长方形或正方形,得出圆锥体的是直角三角形.
故选:B,C.
【点评】此题主要考查立体图形中旋转体,也就是把一个图形绕一条直线旋转得到的图形,要基本的图形特征,才能正确判定.
11.【分析】(1)以三角形较长的直角边为轴旋转一周,形成的图形是高为4厘米底面半径为3厘米的圆锥,根据圆锥的体积公式“V=πr2h”即可求出它的体积.
(2)以三角形较短的直角边为轴旋转一周,形成的图形是高为3厘米底面半径为4厘米的圆锥,根据圆锥的体积公式“V=πr2h”即可求出它的体积.
【解答】解:(1)×3.14×32×4
=×3.14×9×4
=37.68(立方厘米)
答:以三角形较长的直角边为轴旋转一周,形成的图形是高为4厘米底面半径为3厘米的圆锥,这个图形的体积是37.68立方厘米.
(2)×3.14×42×3
=×3.14×16×3
=50.24(立方厘米)
答:以三角形较短的直角边为轴旋转一周,形成的图形是高为3厘米底面半径为4厘米的圆锥,这个图形的体积是50.24立方厘米.
故答案为:高为4厘米底面半径为3厘米的圆锥,37.68;高为3厘米底面半径为4厘米的圆锥,50.24.
【点评】以直角三形一直角边为轴旋转一周可形成以旋转轴为高另一直角边为底面半径的圆锥;求圆锥的体积关键记住公式.
12.【分析】生活中经常先设计一个单一图形或图形的一部分,通过平移、旋转即可形成一幅完整的图案,或设计一个图案的一半,能轴对称画出它的另一半.
【解答】解:生活中利用图形的平移、旋转和轴对称来对图形进行变换设计.
故答案为:平移、旋转、轴对称.
【点评】利用图形的平移、旋转、轴对称,设计图案是常用的方法.
13.【分析】根据旋转的意义,找出图中相邻两个笑脸的眼睛和嘴巴,两个关键处是沿什么方向旋转的,然后再确定旋转的度数即可.
【解答】解:如图所示,小笑脸按
顺时针方向旋转,每次旋转
90度.
故答案为:顺,90.
【点评】本题考查的是图形旋转的变化,解答时关键理清是顺时针还是逆时针旋转,然后再找出旋转度数即可.
14.【分析】因为上图在旋转时,O点保持不动,将底边OA向上移动了,因此三角形A′OB′是三角形AOB绕O点顺时针旋转90度后的图形.
【解答】解:由以上分析:
上图三角形A′OB′是三角形AOB绕O顺时针旋转90度后的图形.
故答案为:√.
【点评】掌握旋转以及顺时针、逆时针的概念,是解答此题的关键.
15.【分析】
根据图示可得,每个大格对应的度数是30°,用60除以30可得指针从“1”绕点O顺时针旋转60°的格子数,进一步可得对着数字几;数出指针从“6”绕点O逆时针旋转到“9”的格子数,然后再乘30即可.
【解答】解:如图所示:
60÷30=2(个)
1+2=3
即,指针从“1”绕点O顺时针旋转60°后指向“3”;
30×9=270(度)
即,指针从“6”绕点O逆时针旋转
270°后指向9.
故答案为:“3”,270.
【点评】本题考查了图形的旋转变化,学生主要看清是顺时针还是逆时针旋转,旋转多少度,和旋转的格子数.
16.【分析】钟面上12个数字把钟面平均分成12份,每份所对应的圆心角是360°÷12=30°,每两个相邻数字间的夹角是30°,即指针从一个数字走到下一个数字时,绕中心轴旋转了30°.3:00分针指向12,3:15分针指向3,分针绕点O按顺时针方向旋转了3个30°,即90°
【解答】解:从3:00到3:15,分针绕点O按顺时针方向旋转了90°.
故答案为:90°.
【点评】关键明白,在钟面上,指针从一个数字旋转到另一个数字,旋转了30°.
三.判断题(共5小题)
17.【分析】根据旋转的特征,一个图形绕某点顺时针旋转90°,某点的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形,即旋转后形状、大小不变,只是位置发生变化.
【解答】解:一个图形绕某一点顺时针旋转90°,其大小、形状不变,位置发生变化,原题的说法是错误的.
故答案为:×.
【点评】此题是考查旋转的特征.图形平移、旋转后形状、大小不变,只是位置发生变化.
18.【分析】钟面上12个数字把钟面平均分成12份,每份所对应的圆心角是360°÷12=30°,即每两个相邻数字间的夹角是30°,即指针从一个数字走到下一个数字时,绕中心轴旋转了30°,从晚上10点到早晨闹钟4点,时针从数字10走到数字12,再走到数字4,走了(12﹣10)+4=6(个)数字,30°×6=180°.
【解答】解:(12﹣10)+4=6
30°×6=180°.
即芳芳晚上10点睡觉,早晨闹钟4点准时响起,则时针在这段时间旋转了180°.
故答案为:×.
【点评】此题是考查钟表的认识与时间的推算.关键明白即指针从一个数字走到下一个数字时绕中心轴旋转多少度,这期间走了几个数字.
19.【分析】旋转:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫作图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变。
据此解答即可。
【解答】解:把一个图形旋转后,图形的形状、大小不变。
故原题说法错误。
故答案为:×。
【点评】此题考查了旋转的意义及在实际当中的运用。
20.【分析】钟面上12个数字,以表芯为旋转点,表针转一圈是360°,被12个数字平均分成12份,每一份也就是两数之间夹角是30°;时钟的时针从“12”顺时针旋转30×3=90度到“3”,据此解答即可。
【解答】解:时钟的时针从“12”顺时针旋转90度到“3”,说法正确。
故答案为:√。
【点评】此题考查了旋转的意义及在实际当中的运用。
21.【分析】通常对一个简单的图案通过平移、旋转、或者做轴对称图形的方法,产生多个相似的图形,从而变成一个美丽的图案.
【解答】解:可以用平移、旋转和作轴对称图形等方法,设计出美丽的图案.
故答案为:√.
【点评】利用平移、旋转、对称设计图形,都要选准基本图案.平移定好平移的格数;对称定好对称轴,选好对称点;旋转选好旋转点,依次沿每次旋转后的基本图的边缘旋转图案.
四.操作题(共2小题)
22.【分析】(1)根据旋转的意义,找出图中梯形的4个关键处,再画出绕A点按顺时针方向旋转90度后的形状即可.
(2)按2:1的比例画出梯形放大后的图形,就是把原三角形的底和高分别扩大到原来的2倍,原三角形的底和高分别是2格和2格,扩大后的三角形的底和高分别是4格和4格.
【解答】解:(1)梯形绕点A按顺时针方向旋转90°后的图形
(2)三角形按2:1放大后的图形
如图所示:
【点评】本题考查了图形的旋转和放大与缩小变化,学生主要看清是顺时针还是逆时针旋转,旋转多少度,以及放大或缩小的倍数.
23.【分析】(1)根据平移的特征,把此图的各顶点先分别向左平移6格,再向下平移3格,依次连结即可得到平移后的图形。
(2)根据旋转的特征,把此图绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
【解答】解:(1)画出将图形先向左平移6格再向下平移3格后的图形(下图红色部分)。
(2)画出将图绕点O顺时针方向旋转90°后得到的图形(下图绿色部分)。
【点评】图形平移注意三要素:即原位置、平移方向、平移距离。图形旋转注意四要素:即原位置、旋转中心、旋转方向、旋转角。
五.解答题(共5小题)
24.【分析】根据旋转的特征,一个图形绕某点按一定的方向旋转一定的度数,某占的位置不动,其余各部分均绕某点按相同的方向旋转相同的度数.据此即可得知:①号图形是绕A点按顺时针方向旋转了90°;②号图形是绕B点按顺时针方向旋转了90°;③号图形是绕C点按逆时针方向旋转了90°;④号图形是绕D点按顺时针方向旋转了90°.
【解答】解:①号图形是绕A点按顺时针方向旋转了90°;②号图形是绕B点按顺时针方向旋转了90°;
③号图形是绕C点按逆时针方向旋转了90°;
④号图形是绕D点按顺时针方向旋转了90°.
故答案为:顺,90,B,90,C,逆,D,顺,90°.
【点评】旋转作图要注意:①旋转方向;②旋转角度.整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动.
25.【分析】(1)根据旋转的特征,把长方形绕点A顺时针旋转90°后,点A的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形;根据旋转后点B的位置及用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即要用数对表示出点B的位置.
(2)图中三角形是一两直角边分别为3格,4格的直角三角形,根据图形放大与缩小的意义,按1:2缩小后的三角形是一两直角边分别为1.5格,2格的直角三角形;分别求原三角形和缩小后三角形的面积,用缩小后三角形的面积除以原三角形的面积(用最简分数表示).
【解答】解:(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形(下图红色部分).旋转后,B点的位置用数对表示是(7、5).
(2)按1:2的比画出三角形缩小后的图形(下图绿色部分).
缩小后的三角形面积:1.5×2÷2=1.5
原三角形面积:3×4÷2=6
1.5÷6=
即缩小后的三角形的面积是原来的.
故答案为:7,5;.
【点评】此题考查的知识点有作旋转一定度数后的图形、点与数对、图形的放大与缩小、三角形面积的计算、分数的意义等.
26.【分析】旋转的要素是旋转方向,旋转中心,旋转角,据此即可解决问题.
【解答】解:根据观察,(1)图形B可以看作是图形A绕点O顺时针旋转90°得到的;
(2)图形C可以看做是图形A绕点O顺时针方向旋转180°所得到的;
(3)图形B绕点O顺时针旋转180°到图形D所在的位置;
(4)图形D可以看作图形C绕点O顺时针方向旋转90°得到的.
故答案为:(1)O;(2)O;顺;180;(3)D;(4)90.
【点评】本题主要考查了旋转的要素,是需要熟记的内容.
27.【分析】根据平移的特征,
(1)图(1)向上平移了4格,
(2)把图(2)中的小船图顶点分别向上平移了5格,
(3)把图(3)中的三角形顶点分别向右平移了7格.
【解答】解:(1)图(1)向上平移了4格,
(2)把图(2)中的小船图顶点分别向上平移了5格,
(3)把图(3)中的三角形顶点分别向右平移了7格.
故答案为:上,4.
【点评】本题主要考查了图形的平移,图形平移后形状、大小不变,只是位置变化.
28.【分析】(1)根据旋转的特征,三角形ABC绕点B逆时针旋转90°,点B的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形.
(2)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可标出点D(2,2)和点E(6,2)的位置.
(3)根据等腰梯形的特征,即可以DE为下底,画一个上底为2厘米,高为3厘米的等腰梯形.
(4)根据梯形的面积计算公式“S=(a+b)h”即可解答.
【解答】解:(1)把三角形绕点B逆时针旋转90o,画出旋转后的图形(三角形A′BC′).
(2)标出点D(2,2)和点E(6,2)的位置(下图).
(3)以DE为下底,画一个上底为2厘米,高为3厘米的等腰梯形(等腰梯形DEFG).
(4)画出的梯形的面积是:
(2+4)×3×
=6×3×
=9(平方厘米).
故答案为:9.
【点评】此题考查的知识有:作旋转一定度数后的图形、数对与位置,等腰梯形的意义、梯形面积的计算等.
