9.2 频率的稳定性 课件(共18张PPT)
文档属性
| 名称 | 9.2 频率的稳定性 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 00:00:00 | ||
图片预览





文档简介
第九章 概率初步
2 频率的稳定性
知识点一 频率及其稳定性
项目
内容
频率的
定义
频率的
稳定性
温馨提示
知识点一 频率及其稳定性
项目
内容
频率的
定义
在n次重复试验中,不确定事件A发生了m次,则比值 一称为事件A发生的频率
频率的
稳定性
在试验次数很大时,事件发生的频率会在一个常数附近摆动,这个性质称为频率的稳定性
温馨提示
频率在一定程度上可以反映随机事件发生的可能性的大小,但频率本身是随机的,在试验前不能确定,无法从根本上来刻画事件发生的可能性的大小
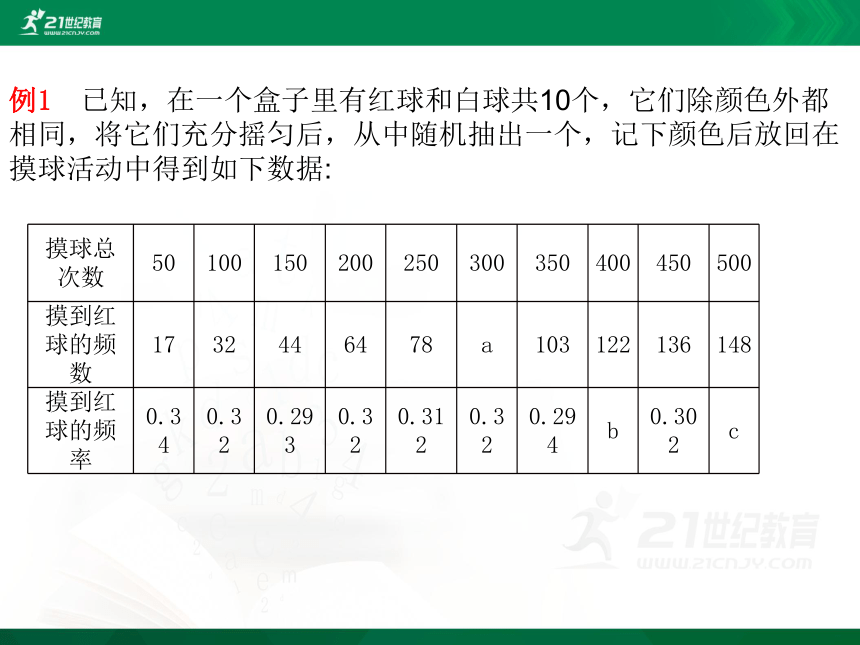
例1 已知,在一个盒子里有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回在摸球活动中得到如下数据:
摸球总次数
50
100
150
200
250
300
350
400
450
500
摸到红球的频数
17
32
44
64
78
a
103
122
136
148
摸到红球的频率
0.34
0.32
0.293
0.32
0.312
0.32
0.294
b
0.302
c
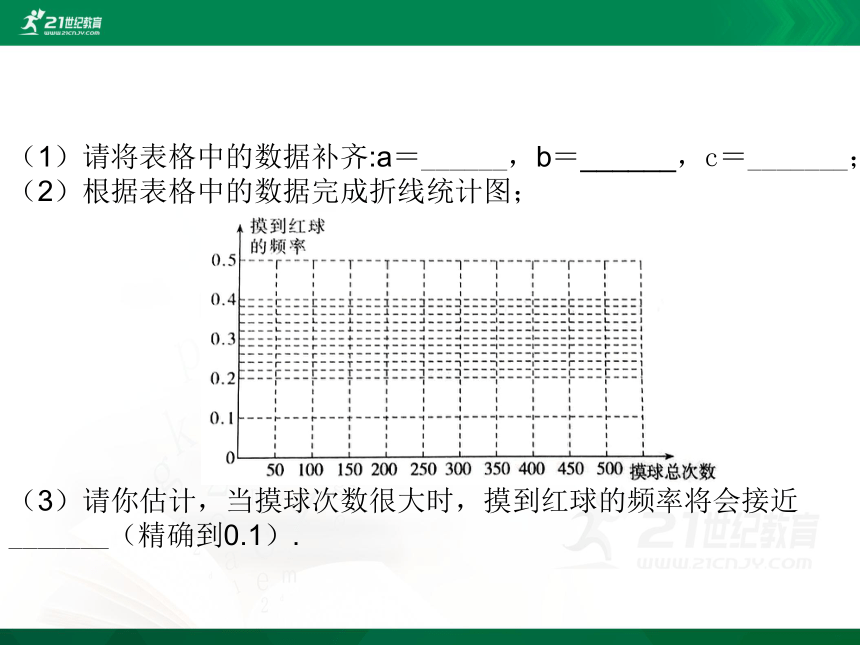
(1)请将表格中的数据补齐:a=______,b=______,c=_______;
(2)根据表格中的数据完成折线统计图;
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近_______(精确到0.1).
解析 (1)a=300×0.32=96,b= =0.305,
c= =0.296.
(2)折线统计图如图所示:
(3)当摸球次数很大时,摸到红球的频率将会接近0.3.
知识点二 用频率来估计某一事件的概率
概率的定义
必然事件的概率
不可能事件的概率
不确定事件的概率
注意
知识点二 用频率来估计某一事件的概率
概率的定义
必然事件的概率
不可能事件的概率
不确定事件的概率
我们把刻画事件A发生的可能性大小的数值,叫做事件A发生的概率,记为P(A)
必然事件发生的概率为1
不可能事件发生的概率为0
不确定事件发生的概率是0与1之间的一个常数
注意
一般地,大量重复的试验中,我们常用不确定事件A发生的频率来估计事件A发生的概率
例2 某种油菜籽在相同条件下的发芽试验结果如下表:
(1)a=________,b=________;
(2)这种油菜籽发芽的概率估计值是多少?请简要说明理由;
(3)如果该种油菜籽发芽后的成秧率为90%,则在相同条件下用10000粒该种油菜籽可得到油菜秧苗约多少棵?
每批粒数n
100
150
200
500
800
1000
发芽的粒数m
65
111
136
345
560
700
发芽的频率
0.65
0.74
0.68
0.69
a
b
解析
(1)a= =0.70,b= =0.70.
(2)这种油菜籽发芽的概率估计值是0.70.理由:在相同条件下,多次试验,某一事件的发生频率近似等于概率.
(3)10000×0.70×90%=6300(棵).
答:10000粒该种油菜籽可得到油菜秧苗约6300棵.
经典例题
题型 利用概率解决实际问题
例 王强与李刚两位同学在学习“概率”时,做抛骰子试验,他们共抛了54次,出现向上点数的次数如下表:
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率;
(2)王强说:“根据试验可知,一次试验中出现向上点数为5的概率最大”李刚分析说:“如果抛540次,那么出现向上点数为6的次数正好是100.”请判断王强和李刚的说法的对错.
向上点数
1
2
3
4
5
6
出现次数
6
9
5
8
16
10
题型 利用概率解决实际问题
解析 (1)出现向上点数为3的频率为 .
出现向上点数为5的频率为= .
(2)王强和李刚的说法都不对.
易错易混
易错点 不能正确理解频率稳定性的含义
在大量重复试验的情况下,一般事件发生的频率都会在一个常数附近摆动,因此,可以用这个常数估计该事件的概率.
易错点 不能正确理解频率稳定性的含义
在大量重复试验的情况下,一般事件发生的频率都会在一个常数附近摆动,因此,可以用这个常数估计该事件的概率.
例 小明在抛啤酒瓶瓶盖(规定带字的一面为正)时,共抛了10次,结果有7次是正面朝上,于是他说:“在抛啤酒瓶瓶盖时,正面朝上的概率是 .”你认为他的说法正确吗?为什么?
易错点 不能正确理解频率稳定性的含义
在大量重复试验的情况下,一般事件发生的频率都会在一个常数附近摆动,因此,可以用这个常数估计该事件的概率.
例 小明在抛啤酒瓶瓶盖(规定带字的一面为正)时,共抛了10次,结果有7次是正面朝上,于是他说:“在抛啤酒瓶瓶盖时,正面朝上的概率是 .”你认为他的说法正确吗?为什么?
解析 不正确理由如下:
他做的试验次数太少,不能用事件的频率估计概率,只有试验次数足够多时,事件的频率值才大约与其概率值相近.
易错点 不能正确理解频率稳定性的含义
在大量重复试验的情况下,一般事件发生的频率都会在一个常数附近摆动,因此,可以用这个常数估计该事件的概率.
例 小明在抛啤酒瓶瓶盖(规定带字的一面为正)时,共抛了10次,结果有7次是正面朝上,于是他说:“在抛啤酒瓶瓶盖时,正面朝上的概率是 .”你认为他的说法正确吗?为什么?
解析 不正确理由如下:
他做的试验次数太少,不能用事件的频率估计概率,只有试验次数足够多时,事件的频率值才大约与其概率值相近.
易错分析 用频率估计概率,试验次数必须足够多.本题不仅试验次数太少,而且本题中的瓶盖的质地也不是均匀的,从而偶然性因素起了作用本题易错认为小明的说法是正确的.
2 频率的稳定性
知识点一 频率及其稳定性
项目
内容
频率的
定义
频率的
稳定性
温馨提示
知识点一 频率及其稳定性
项目
内容
频率的
定义
在n次重复试验中,不确定事件A发生了m次,则比值 一称为事件A发生的频率
频率的
稳定性
在试验次数很大时,事件发生的频率会在一个常数附近摆动,这个性质称为频率的稳定性
温馨提示
频率在一定程度上可以反映随机事件发生的可能性的大小,但频率本身是随机的,在试验前不能确定,无法从根本上来刻画事件发生的可能性的大小
例1 已知,在一个盒子里有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回在摸球活动中得到如下数据:
摸球总次数
50
100
150
200
250
300
350
400
450
500
摸到红球的频数
17
32
44
64
78
a
103
122
136
148
摸到红球的频率
0.34
0.32
0.293
0.32
0.312
0.32
0.294
b
0.302
c
(1)请将表格中的数据补齐:a=______,b=______,c=_______;
(2)根据表格中的数据完成折线统计图;
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近_______(精确到0.1).
解析 (1)a=300×0.32=96,b= =0.305,
c= =0.296.
(2)折线统计图如图所示:
(3)当摸球次数很大时,摸到红球的频率将会接近0.3.
知识点二 用频率来估计某一事件的概率
概率的定义
必然事件的概率
不可能事件的概率
不确定事件的概率
注意
知识点二 用频率来估计某一事件的概率
概率的定义
必然事件的概率
不可能事件的概率
不确定事件的概率
我们把刻画事件A发生的可能性大小的数值,叫做事件A发生的概率,记为P(A)
必然事件发生的概率为1
不可能事件发生的概率为0
不确定事件发生的概率是0与1之间的一个常数
注意
一般地,大量重复的试验中,我们常用不确定事件A发生的频率来估计事件A发生的概率
例2 某种油菜籽在相同条件下的发芽试验结果如下表:
(1)a=________,b=________;
(2)这种油菜籽发芽的概率估计值是多少?请简要说明理由;
(3)如果该种油菜籽发芽后的成秧率为90%,则在相同条件下用10000粒该种油菜籽可得到油菜秧苗约多少棵?
每批粒数n
100
150
200
500
800
1000
发芽的粒数m
65
111
136
345
560
700
发芽的频率
0.65
0.74
0.68
0.69
a
b
解析
(1)a= =0.70,b= =0.70.
(2)这种油菜籽发芽的概率估计值是0.70.理由:在相同条件下,多次试验,某一事件的发生频率近似等于概率.
(3)10000×0.70×90%=6300(棵).
答:10000粒该种油菜籽可得到油菜秧苗约6300棵.
经典例题
题型 利用概率解决实际问题
例 王强与李刚两位同学在学习“概率”时,做抛骰子试验,他们共抛了54次,出现向上点数的次数如下表:
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率;
(2)王强说:“根据试验可知,一次试验中出现向上点数为5的概率最大”李刚分析说:“如果抛540次,那么出现向上点数为6的次数正好是100.”请判断王强和李刚的说法的对错.
向上点数
1
2
3
4
5
6
出现次数
6
9
5
8
16
10
题型 利用概率解决实际问题
解析 (1)出现向上点数为3的频率为 .
出现向上点数为5的频率为= .
(2)王强和李刚的说法都不对.
易错易混
易错点 不能正确理解频率稳定性的含义
在大量重复试验的情况下,一般事件发生的频率都会在一个常数附近摆动,因此,可以用这个常数估计该事件的概率.
易错点 不能正确理解频率稳定性的含义
在大量重复试验的情况下,一般事件发生的频率都会在一个常数附近摆动,因此,可以用这个常数估计该事件的概率.
例 小明在抛啤酒瓶瓶盖(规定带字的一面为正)时,共抛了10次,结果有7次是正面朝上,于是他说:“在抛啤酒瓶瓶盖时,正面朝上的概率是 .”你认为他的说法正确吗?为什么?
易错点 不能正确理解频率稳定性的含义
在大量重复试验的情况下,一般事件发生的频率都会在一个常数附近摆动,因此,可以用这个常数估计该事件的概率.
例 小明在抛啤酒瓶瓶盖(规定带字的一面为正)时,共抛了10次,结果有7次是正面朝上,于是他说:“在抛啤酒瓶瓶盖时,正面朝上的概率是 .”你认为他的说法正确吗?为什么?
解析 不正确理由如下:
他做的试验次数太少,不能用事件的频率估计概率,只有试验次数足够多时,事件的频率值才大约与其概率值相近.
易错点 不能正确理解频率稳定性的含义
在大量重复试验的情况下,一般事件发生的频率都会在一个常数附近摆动,因此,可以用这个常数估计该事件的概率.
例 小明在抛啤酒瓶瓶盖(规定带字的一面为正)时,共抛了10次,结果有7次是正面朝上,于是他说:“在抛啤酒瓶瓶盖时,正面朝上的概率是 .”你认为他的说法正确吗?为什么?
解析 不正确理由如下:
他做的试验次数太少,不能用事件的频率估计概率,只有试验次数足够多时,事件的频率值才大约与其概率值相近.
易错分析 用频率估计概率,试验次数必须足够多.本题不仅试验次数太少,而且本题中的瓶盖的质地也不是均匀的,从而偶然性因素起了作用本题易错认为小明的说法是正确的.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
