1.1.2空间向量的数量积运算(共23张PPT)-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第一册课件
文档属性
| 名称 | 1.1.2空间向量的数量积运算(共23张PPT)-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第一册课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-16 11:23:21 | ||
图片预览





文档简介
1.1.2空间向量的数量积运算
在空间任取一点O,作???????? =????,
???????? =???? ,则∠AOB叫做向量????, ????夹角,记作.
?
复习引入
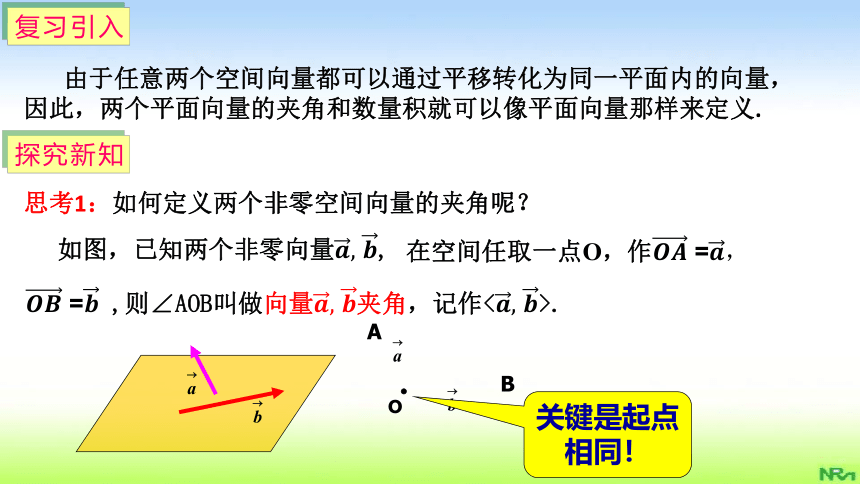
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个平面向量的夹角和数量积就可以像平面向量那样来定义.
探究新知
思考1:如何定义两个非零空间向量的夹角呢?
如图,已知两个非零向量????, ????,
?
o
B
A
关键是起点相同!
解惑提高
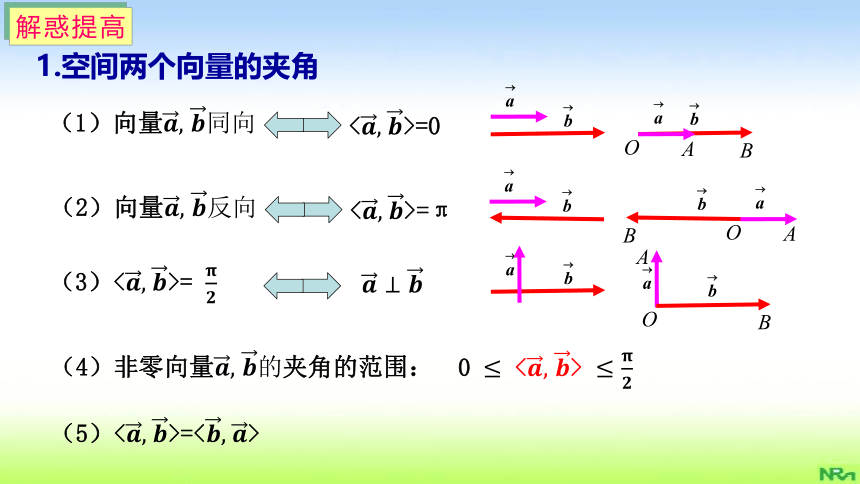
1.空间两个向量的夹角
(1)向量????, ????同向
?
O
A
B
=0
?
O
A
B
O
A
B
(2)向量????, ????反向
?
=π
?
(3)= ????????
?
????⊥ ????
?
(4)非零向量????, ????的夹角的范围:
?
0?≤ ≤????????
?
(5)=
?
探究新知
思考2:如何定义两个非零空间向量的数量积呢?
2. 两个向量的数量积
(1)定义:已知两个非零向量????, ????,则 |????|·|????|cos叫做????, ????的数量积,记作????·????.即
????·????= |????|·|????|cos .
?
注意①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于0.即
0·????=0
?
两个向量数量积的性质
①若a,b是非零向量,则a⊥b?_______
②若a与b同向,则a·b=______;若反向,则a·b=________.
③特别地,a·a=____或|a|=
④若〈a,b〉为a,b的夹角,则cos〈a,b〉=_______
⑤|a·b|≤|a|·|b|
3. 空间向量的数量积的性质
a·b=0
|a|·|b|
-|a|·|b|
|a|2
????·????= |????|·|????|cos
?
解惑提高
向量数量积的运算不满足消去律、作商和乘法的结合律 ,即a·b=a·c?b=c,a·b=k?b=????????,(a·b)·c=a·(b·c)都不成立.
?
解惑提高
4. 空间向量数量积运算律
(1)a·b=
(2)(λa)·b=
(3) a·(b+c)=
λ(a·b)
=a·(λb)
b·a
a·b+a·c
(交换律)
(数乘结合律)
(分配律)
思考3:对应向量a,b,c,(a·b ) · c= a · (b·c)成立吗?
探究新知
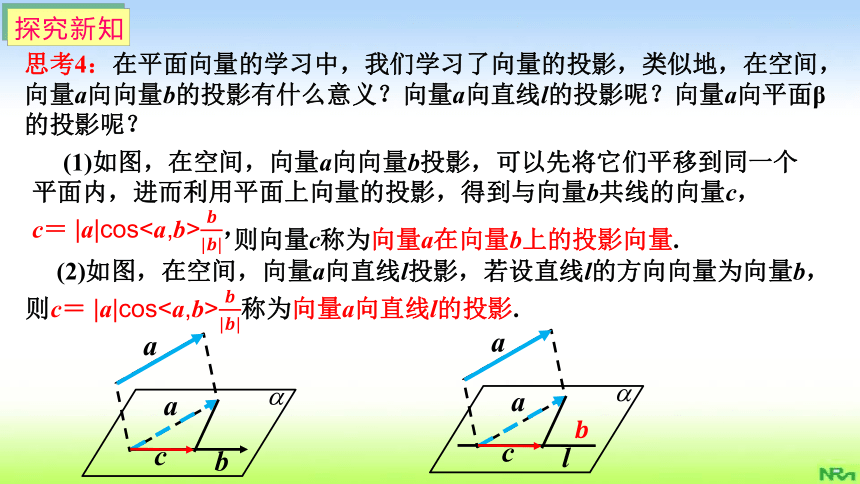
思考4:在平面向量的学习中,我们学习了向量的投影,类似地,在空间,向量a向向量b的投影有什么意义?向量a向直线l的投影呢?向量a向平面β的投影呢?
(1)如图,在空间,向量a向向量b投影,可以先将它们平移到同一个平面内,进而利用平面上向量的投影,得到与向量b共线的向量c,
c= |a|cos????|????|,
?
a
a
c
b
则向量c称为向量a在向量b上的投影向量.
(2)如图,在空间,向量a向直线l投影,若设直线l的方向向量为向量b,
a
a
c
l
????
?
则c= |a|cos????|????|称为向量a向直线l的投影.
?
则向量????′????′称为向量a在平面β上的投影向量.
?
探究新知
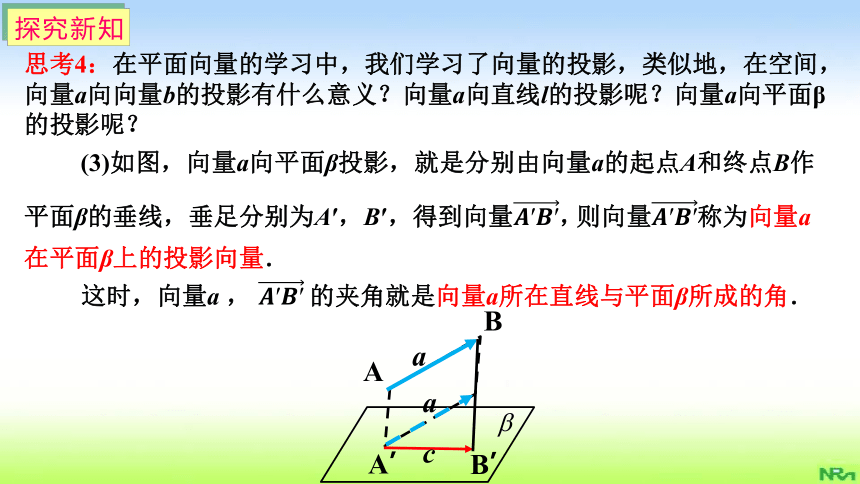
思考4:在平面向量的学习中,我们学习了向量的投影,类似地,在空间,向量a向向量b的投影有什么意义?向量a向直线l的投影呢?向量a向平面β的投影呢?
(3)如图,向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A′,B′,得到向量????′????′,
?
这时,向量a , ????′????′?的夹角就是向量a所在直线与平面β所成的角.
?
a
a
c
A
B
A’
B’
小试牛刀
小试牛刀
2.已知向量????, ????,满足|????|=????,|????|=????,?????????=????,则????+????=_____.
?
解:由?????????????=??????????????????????+????????=????,代入|????|=????,|????|=????,得
?
?????????=-2
?
∴????+????????=????????+?????????????+????????=1
?
∴?????+????=?????.
?
典型例题
空间向量数量积的运算
????′
?
????′
?
????′
?
????′
?
????
?
????
?
????
?
????
?
例1 如图,在平行六面体?????????????????????′????′????′????′中,
????????=????,????????=????,????????′=????,∠????????????=????????°,∠????????????′=∠????????????′=????????°,求
(1) ?????????????????;(2) ????????′的长(精确到0.1).
?
解: (1) ?????????????????=|????????||????????|????????????
?
=5×????×????????????????????°
?
=7.5
?
(2) ∵????????′=????????+????????+????????′
?
∴|????????′|2=(????????+????????+????????′) 2
?
=|????????|2+ |????????|2+ |????????′|2+2(?????????????????+?????????????????′+?????????????????′)
?
=????2+ ????2+ ????2+2(????×????×??????????????????°+????×????×????????????????????°+????×????×????????????????????°)
?
=98+562
?
∴?????????′≈????????.????
?
总结提升
在几何体中求空间向量的数量积的步骤
(1)首先将各向量分解成已知模和夹角的向量的组合形式.
(2)利用向量的运算律将数量积展开,转化成已知模和夹角的向量的数量积.
(3)根据向量的方向,正确求出向量的夹角及向量的模.
(4)代入公式a·b=|a||b|cos〈a,b〉求解.
O
A
B
C
小试牛刀
O
A
B
C
已知正四面体OABC的棱长为1,求:
小试牛刀
典型例题
利用空间向量数量积证明垂直关系
例2 如图,????,????是平面????内的两条相交直线.如果????⊥????, ????⊥?????,求证: ????⊥????.
?
????
?
????
?
????
?
?????
?
????
?
分析:要证明????⊥????,就是要证明????垂直于????内的任意一条直线????
直线与平面平行的定义.如果我们能在????和????,????之间建立某种联系,并由????⊥????, ????⊥?????, 得到????⊥????,那么就能解决问题.
?
????
?
????
?
????
?
????
?
典型例题
利用空间向量数量积证明垂直关系
例2 如图,????,????是平面????内的两条相交直线.如果????⊥????, ????⊥?????,求证: ????⊥????.
?
????
?
????
?
????
?
?????
?
????
?
????
?
????
?
????
?
????
?
证明:在平面????内作任意一条直线????,分别在直线????, ????, ????, ????上取非零向量????,????,????,????.
?
因为直线????与????相交,所以向量????,????不平行.由向量共面的充要条件可知,存在唯一的有序实数对(????,????),使
?
????=????????+????????.
?
将上式两边分别与向量????作数量积运算,得
?
??????????=??????????????+??????????????.
?
因为??????????=????,??????????=0,所以??????????=0.
?
所以????⊥?????.
?
这就证明了直线????垂直于平面????内的任意一条直线,所以????⊥????.
?
总结提升
用向量法证明空间中垂直关系的一般步骤:
(1)把几何问题转化为向量问题;
(2)用已知向量表示所证向量;
(3)结合数量积公式和运算律证明数量积为0;
(4)将向量问题回归到几何问题.
已知:PO、PA分别是平面α的垂线、斜线,AO是PA在平面α内的射影,l?α,且l⊥OA.求证:l⊥PA.
因为l⊥OA,
所以l⊥PA.
小试牛刀
利用数量积求夹角
例3 BB1⊥平面ABC,且△ABC是∠B=90°的等腰直角三角形,?ABB1A1、?BB1C1C的对角线都分别相互垂直且相等,若AB=a,求异面直线BA1与AC所成的角.
因为AB⊥BC,BB1⊥AB,BB1⊥BC,
典型例题
总结提升
用向量法求异面直线夹角的方法:
课堂小结
在空间任取一点O,作???????? =????,
???????? =???? ,则∠AOB叫做向量????, ????夹角,记作.
?
复习引入
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个平面向量的夹角和数量积就可以像平面向量那样来定义.
探究新知
思考1:如何定义两个非零空间向量的夹角呢?
如图,已知两个非零向量????, ????,
?
o
B
A
关键是起点相同!
解惑提高
1.空间两个向量的夹角
(1)向量????, ????同向
?
O
A
B
=0
?
O
A
B
O
A
B
(2)向量????, ????反向
?
=π
?
(3)= ????????
?
????⊥ ????
?
(4)非零向量????, ????的夹角的范围:
?
0?≤ ≤????????
?
(5)=
?
探究新知
思考2:如何定义两个非零空间向量的数量积呢?
2. 两个向量的数量积
(1)定义:已知两个非零向量????, ????,则 |????|·|????|cos叫做????, ????的数量积,记作????·????.即
????·????= |????|·|????|cos .
?
注意①两个向量的数量积是数量,而不是向量.
②零向量与任意向量的数量积等于0.即
0·????=0
?
两个向量数量积的性质
①若a,b是非零向量,则a⊥b?_______
②若a与b同向,则a·b=______;若反向,则a·b=________.
③特别地,a·a=____或|a|=
④若〈a,b〉为a,b的夹角,则cos〈a,b〉=_______
⑤|a·b|≤|a|·|b|
3. 空间向量的数量积的性质
a·b=0
|a|·|b|
-|a|·|b|
|a|2
????·????= |????|·|????|cos
?
解惑提高
向量数量积的运算不满足消去律、作商和乘法的结合律 ,即a·b=a·c?b=c,a·b=k?b=????????,(a·b)·c=a·(b·c)都不成立.
?
解惑提高
4. 空间向量数量积运算律
(1)a·b=
(2)(λa)·b=
(3) a·(b+c)=
λ(a·b)
=a·(λb)
b·a
a·b+a·c
(交换律)
(数乘结合律)
(分配律)
思考3:对应向量a,b,c,(a·b ) · c= a · (b·c)成立吗?
探究新知
思考4:在平面向量的学习中,我们学习了向量的投影,类似地,在空间,向量a向向量b的投影有什么意义?向量a向直线l的投影呢?向量a向平面β的投影呢?
(1)如图,在空间,向量a向向量b投影,可以先将它们平移到同一个平面内,进而利用平面上向量的投影,得到与向量b共线的向量c,
c= |a|cos
?
a
a
c
b
则向量c称为向量a在向量b上的投影向量.
(2)如图,在空间,向量a向直线l投影,若设直线l的方向向量为向量b,
a
a
c
l
????
?
则c= |a|cos
?
则向量????′????′称为向量a在平面β上的投影向量.
?
探究新知
思考4:在平面向量的学习中,我们学习了向量的投影,类似地,在空间,向量a向向量b的投影有什么意义?向量a向直线l的投影呢?向量a向平面β的投影呢?
(3)如图,向量a向平面β投影,就是分别由向量a的起点A和终点B作平面β的垂线,垂足分别为A′,B′,得到向量????′????′,
?
这时,向量a , ????′????′?的夹角就是向量a所在直线与平面β所成的角.
?
a
a
c
A
B
A’
B’
小试牛刀
小试牛刀
2.已知向量????, ????,满足|????|=????,|????|=????,?????????=????,则????+????=_____.
?
解:由?????????????=??????????????????????+????????=????,代入|????|=????,|????|=????,得
?
?????????=-2
?
∴????+????????=????????+?????????????+????????=1
?
∴?????+????=?????.
?
典型例题
空间向量数量积的运算
????′
?
????′
?
????′
?
????′
?
????
?
????
?
????
?
????
?
例1 如图,在平行六面体?????????????????????′????′????′????′中,
????????=????,????????=????,????????′=????,∠????????????=????????°,∠????????????′=∠????????????′=????????°,求
(1) ?????????????????;(2) ????????′的长(精确到0.1).
?
解: (1) ?????????????????=|????????||????????|????????????
?
=5×????×????????????????????°
?
=7.5
?
(2) ∵????????′=????????+????????+????????′
?
∴|????????′|2=(????????+????????+????????′) 2
?
=|????????|2+ |????????|2+ |????????′|2+2(?????????????????+?????????????????′+?????????????????′)
?
=????2+ ????2+ ????2+2(????×????×??????????????????°+????×????×????????????????????°+????×????×????????????????????°)
?
=98+562
?
∴?????????′≈????????.????
?
总结提升
在几何体中求空间向量的数量积的步骤
(1)首先将各向量分解成已知模和夹角的向量的组合形式.
(2)利用向量的运算律将数量积展开,转化成已知模和夹角的向量的数量积.
(3)根据向量的方向,正确求出向量的夹角及向量的模.
(4)代入公式a·b=|a||b|cos〈a,b〉求解.
O
A
B
C
小试牛刀
O
A
B
C
已知正四面体OABC的棱长为1,求:
小试牛刀
典型例题
利用空间向量数量积证明垂直关系
例2 如图,????,????是平面????内的两条相交直线.如果????⊥????, ????⊥?????,求证: ????⊥????.
?
????
?
????
?
????
?
?????
?
????
?
分析:要证明????⊥????,就是要证明????垂直于????内的任意一条直线????
直线与平面平行的定义.如果我们能在????和????,????之间建立某种联系,并由????⊥????, ????⊥?????, 得到????⊥????,那么就能解决问题.
?
????
?
????
?
????
?
????
?
典型例题
利用空间向量数量积证明垂直关系
例2 如图,????,????是平面????内的两条相交直线.如果????⊥????, ????⊥?????,求证: ????⊥????.
?
????
?
????
?
????
?
?????
?
????
?
????
?
????
?
????
?
????
?
证明:在平面????内作任意一条直线????,分别在直线????, ????, ????, ????上取非零向量????,????,????,????.
?
因为直线????与????相交,所以向量????,????不平行.由向量共面的充要条件可知,存在唯一的有序实数对(????,????),使
?
????=????????+????????.
?
将上式两边分别与向量????作数量积运算,得
?
??????????=??????????????+??????????????.
?
因为??????????=????,??????????=0,所以??????????=0.
?
所以????⊥?????.
?
这就证明了直线????垂直于平面????内的任意一条直线,所以????⊥????.
?
总结提升
用向量法证明空间中垂直关系的一般步骤:
(1)把几何问题转化为向量问题;
(2)用已知向量表示所证向量;
(3)结合数量积公式和运算律证明数量积为0;
(4)将向量问题回归到几何问题.
已知:PO、PA分别是平面α的垂线、斜线,AO是PA在平面α内的射影,l?α,且l⊥OA.求证:l⊥PA.
因为l⊥OA,
所以l⊥PA.
小试牛刀
利用数量积求夹角
例3 BB1⊥平面ABC,且△ABC是∠B=90°的等腰直角三角形,?ABB1A1、?BB1C1C的对角线都分别相互垂直且相等,若AB=a,求异面直线BA1与AC所成的角.
因为AB⊥BC,BB1⊥AB,BB1⊥BC,
典型例题
总结提升
用向量法求异面直线夹角的方法:
课堂小结
