圆周角
图片预览






文档简介
(共22张PPT)
圆 周 角
观察
下图是一个圆柱形的海洋馆的横截面示意图,人们可以通过玻璃窗AB观看窗内的海洋动物 , 同学甲站在圆心O的位置,同学乙站在位置C, 同学丙站在位置D,同学丁站在位置E,他们都说自己的位置好,如果你是海洋馆的工作人员,你怎么评价他们的意见?
乙(C)
B
A
甲(0)
丙(D)
(
丁(E)
1
2
3
4
6
5
.
0
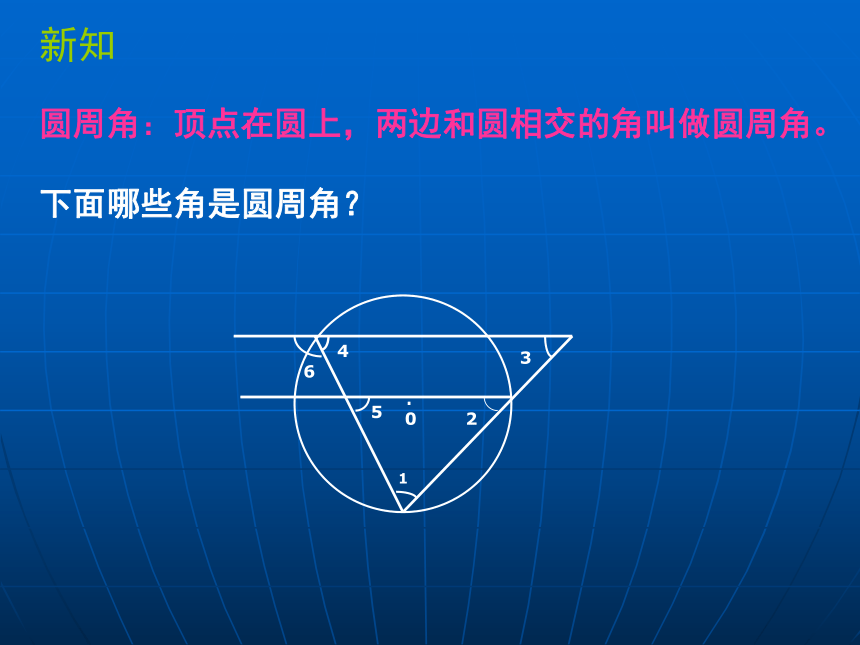
圆周角:顶点在圆上,两边和圆相交的角叫做圆周角。
下面哪些角是圆周角?
新知
乙(C)
B
A
甲(0)
丙(D)
丁(E)
实验
∠ C = ∠ D = ∠E = ∠AOB
实验 猜想
通过测量我们发现:
2
1
AB所对圆周角相等
AB所对圆心角
同一条弧所对的圆周角相等,都等于该弧所对的圆心角的一半。
(
(
等于
一半
在你的圆形纸片上任意取一段弧,画出这段弧所对的圆心角和任意的一个圆周角,然后根据你所画的图形分小组试着探索说明该弧所对的圆周角等于圆心角的一半成立的理由。
动手实践 验证猜想
O
A
B
O
C
A
B
C
O
A
B
C
O
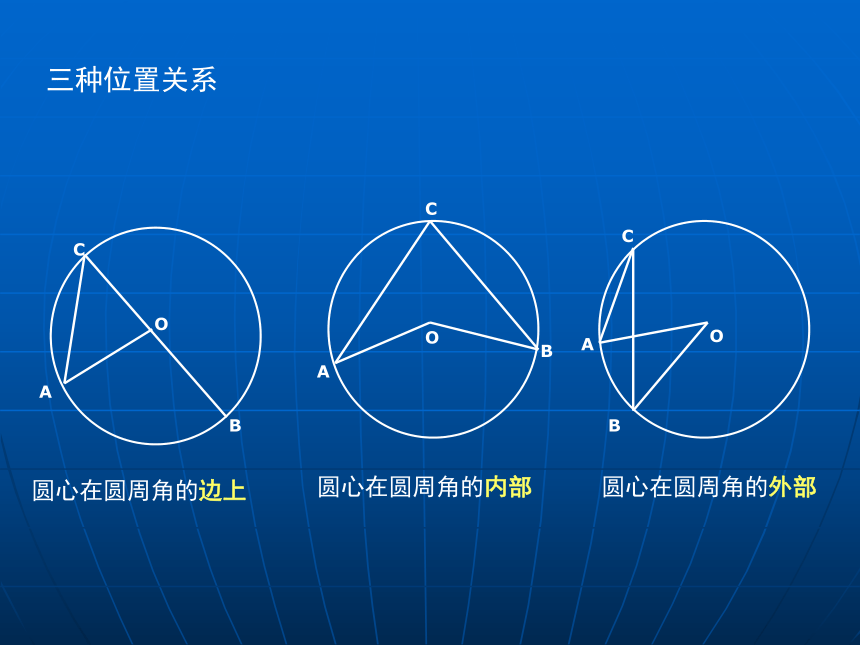
圆心在圆周角的边上
圆心在圆周角的内部
圆心在圆周角的外部
三种位置关系
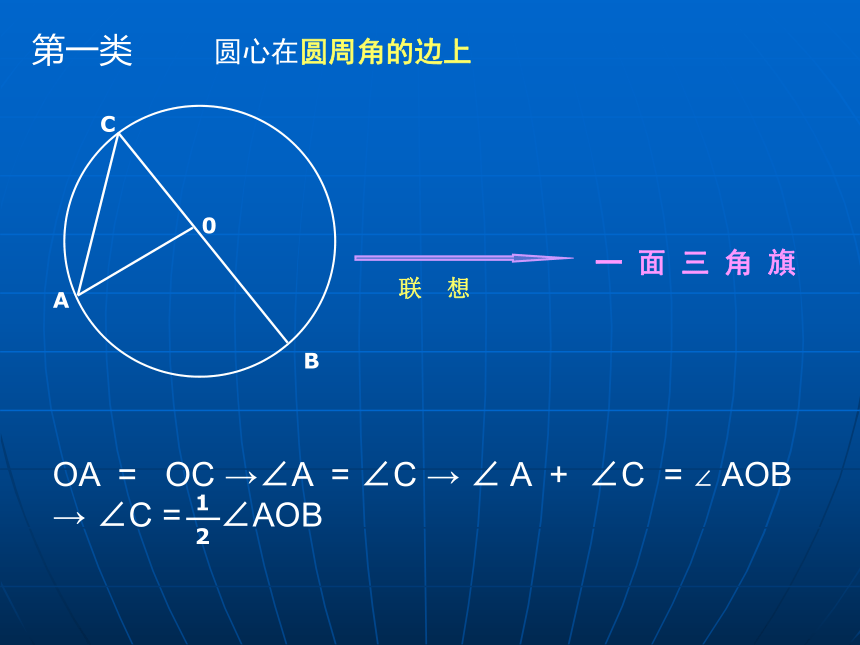
OA = OC →∠A = ∠C → ∠ A + ∠C = ∠ AOB → ∠C = ∠AOB
A
C
0
B
联 想
一 面 三 角 旗
2
1
第一类 圆心在圆周角的边上
第二类 圆心在圆周角的内部
A
C
B
0
D
联 想
作 直 径
两面合并的三角旗
∠ ACB =∠ACD+∠ BCD →∠ ACD= ∠AOD ,∠ BCD = ∠ BOD
(∠AOD+ ∠ BOD ) → ∠AOB
2
1
2
1
2
1
2
1
第三类:圆心在圆周角外部
A
B
C
0
作 直 径
联 想
两面三角旗叠合
D
∠ACB =∠ACD -∠BCD →∠ACD= ∠AOD,∠BCD= ∠BOD
(∠AOD - ∠BOD) ∠AOB
2
1
2
1
2
1
2
1
同弧所对的圆周角相等,都等于该弧所对的圆心角的一半。
猜想成立
阅读材料 消化新知 思维拓展
1.阅读教材第92页内容,理解掌握圆周角定理:在同圆或者等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;半圆(或直径)所对的圆周角是直角,90度的圆周角所对的弦是直径;
2.自我解决教材92页的“思考”;
3.阅读教材93页的“例2”,注意其格式和原理。
1.判断
①同弧或等弧所对的圆周角一定相等
②在同圆或等圆中等弦所对的圆周角相等
③相等的圆周角所对的弧相等
④90度的圆周角所对的弦是圆内最大的弦
2.思考:
同一圆内若两条弧相等,则你可以得到哪些结论?
在等圆中是否有同样结论?
试一试
对
对
对
错
弦 圆心角 圆周角都相等
所对的:
在同圆或者等圆中,如果以上有一组量相等,则其他的三组量也是相等的
解:由题意可得:
OA ⊥ BC
AC =AB
∠ ADC = ∠ AOB
∠AOB = 50O
∠ADC = 25O
0
C
B
A
D
(
)
例2:
如图,在⊙O中AO⊥ BC , ∠AOB=50O试确定∠ADC大小
∟
1
2
1. 如图1找出图中所有相等的圆周角。
2. 在圆中一条弧所对的圆心角和圆周角分别为(2x + 100)0和(5x – 30)0则这条弧所对的圆心角的度数为 ,圆周角的度数为 。
3.如图2,⊙O中弦AB,CD相交于点P,∠A=400,∠APD=750求∠B的度数
巩 固 提 高
1
2
3
4
5
6
7
8
1
A
P
C
B
D
2
.
0
.
0
1400
700
350
∠B= ∠C → ∠A+ ∠C=750 →C=350 →B=35O
400
750
解决问题
好了, 现在你如果是海洋馆的工作人员,你怎么评价他们的意见?
乙(C)
丙(D)
甲(0)
A
B
丁(E)
如图 :“世界杯”赛场上李铁、邵佳一、 郝海东三名队员互相配合向对方球门进攻,当李带球冲到如图C点时,邵、郝也分别跟随冲到图中的D点、E点,从射门的角度大小考虑,李应把球传给谁好?请你从数学角度帮忙合情说理、分析说明。
A
E
C
B
D
课外延拓
.
O
在同圆或者等圆中,同弧或等弧所对的圆周 角相等,都等于这条弧所对的圆心角的一半。
推论 :半圆(或直径)所对的圆周角是直角,90度的圆周角所对的弦是直径。
数学思想:
特殊
一般
实验
观察
猜想
验证
我的收获:
圆周角定理:
A
D
B
C
A
A
B
C
0
B
.
0
作业
1.在⊙O中,∠BOC=100o,则弦BC所对的圆周角是 度.
2.已知如图A ,在⊙O中AB=AC=2cm. ∠BDC=60O。求△ABC的周长
3.如图B,在⊙O中∠ACB,∠AOB分别是弦AB所对的圆周角和圆心角,
求∠ ACB+∠OAB的度数。
∟
再 见
常宁五中 何炜频
圆 周 角
观察
下图是一个圆柱形的海洋馆的横截面示意图,人们可以通过玻璃窗AB观看窗内的海洋动物 , 同学甲站在圆心O的位置,同学乙站在位置C, 同学丙站在位置D,同学丁站在位置E,他们都说自己的位置好,如果你是海洋馆的工作人员,你怎么评价他们的意见?
乙(C)
B
A
甲(0)
丙(D)
(
丁(E)
1
2
3
4
6
5
.
0
圆周角:顶点在圆上,两边和圆相交的角叫做圆周角。
下面哪些角是圆周角?
新知
乙(C)
B
A
甲(0)
丙(D)
丁(E)
实验
∠ C = ∠ D = ∠E = ∠AOB
实验 猜想
通过测量我们发现:
2
1
AB所对圆周角相等
AB所对圆心角
同一条弧所对的圆周角相等,都等于该弧所对的圆心角的一半。
(
(
等于
一半
在你的圆形纸片上任意取一段弧,画出这段弧所对的圆心角和任意的一个圆周角,然后根据你所画的图形分小组试着探索说明该弧所对的圆周角等于圆心角的一半成立的理由。
动手实践 验证猜想
O
A
B
O
C
A
B
C
O
A
B
C
O
圆心在圆周角的边上
圆心在圆周角的内部
圆心在圆周角的外部
三种位置关系
OA = OC →∠A = ∠C → ∠ A + ∠C = ∠ AOB → ∠C = ∠AOB
A
C
0
B
联 想
一 面 三 角 旗
2
1
第一类 圆心在圆周角的边上
第二类 圆心在圆周角的内部
A
C
B
0
D
联 想
作 直 径
两面合并的三角旗
∠ ACB =∠ACD+∠ BCD →∠ ACD= ∠AOD ,∠ BCD = ∠ BOD
(∠AOD+ ∠ BOD ) → ∠AOB
2
1
2
1
2
1
2
1
第三类:圆心在圆周角外部
A
B
C
0
作 直 径
联 想
两面三角旗叠合
D
∠ACB =∠ACD -∠BCD →∠ACD= ∠AOD,∠BCD= ∠BOD
(∠AOD - ∠BOD) ∠AOB
2
1
2
1
2
1
2
1
同弧所对的圆周角相等,都等于该弧所对的圆心角的一半。
猜想成立
阅读材料 消化新知 思维拓展
1.阅读教材第92页内容,理解掌握圆周角定理:在同圆或者等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;半圆(或直径)所对的圆周角是直角,90度的圆周角所对的弦是直径;
2.自我解决教材92页的“思考”;
3.阅读教材93页的“例2”,注意其格式和原理。
1.判断
①同弧或等弧所对的圆周角一定相等
②在同圆或等圆中等弦所对的圆周角相等
③相等的圆周角所对的弧相等
④90度的圆周角所对的弦是圆内最大的弦
2.思考:
同一圆内若两条弧相等,则你可以得到哪些结论?
在等圆中是否有同样结论?
试一试
对
对
对
错
弦 圆心角 圆周角都相等
所对的:
在同圆或者等圆中,如果以上有一组量相等,则其他的三组量也是相等的
解:由题意可得:
OA ⊥ BC
AC =AB
∠ ADC = ∠ AOB
∠AOB = 50O
∠ADC = 25O
0
C
B
A
D
(
)
例2:
如图,在⊙O中AO⊥ BC , ∠AOB=50O试确定∠ADC大小
∟
1
2
1. 如图1找出图中所有相等的圆周角。
2. 在圆中一条弧所对的圆心角和圆周角分别为(2x + 100)0和(5x – 30)0则这条弧所对的圆心角的度数为 ,圆周角的度数为 。
3.如图2,⊙O中弦AB,CD相交于点P,∠A=400,∠APD=750求∠B的度数
巩 固 提 高
1
2
3
4
5
6
7
8
1
A
P
C
B
D
2
.
0
.
0
1400
700
350
∠B= ∠C → ∠A+ ∠C=750 →C=350 →B=35O
400
750
解决问题
好了, 现在你如果是海洋馆的工作人员,你怎么评价他们的意见?
乙(C)
丙(D)
甲(0)
A
B
丁(E)
如图 :“世界杯”赛场上李铁、邵佳一、 郝海东三名队员互相配合向对方球门进攻,当李带球冲到如图C点时,邵、郝也分别跟随冲到图中的D点、E点,从射门的角度大小考虑,李应把球传给谁好?请你从数学角度帮忙合情说理、分析说明。
A
E
C
B
D
课外延拓
.
O
在同圆或者等圆中,同弧或等弧所对的圆周 角相等,都等于这条弧所对的圆心角的一半。
推论 :半圆(或直径)所对的圆周角是直角,90度的圆周角所对的弦是直径。
数学思想:
特殊
一般
实验
观察
猜想
验证
我的收获:
圆周角定理:
A
D
B
C
A
A
B
C
0
B
.
0
作业
1.在⊙O中,∠BOC=100o,则弦BC所对的圆周角是 度.
2.已知如图A ,在⊙O中AB=AC=2cm. ∠BDC=60O。求△ABC的周长
3.如图B,在⊙O中∠ACB,∠AOB分别是弦AB所对的圆周角和圆心角,
求∠ ACB+∠OAB的度数。
∟
再 见
常宁五中 何炜频
同课章节目录
