2020-2021学年北师大版八年级数学下册第一章 1.1等腰三角形 同步测试题(word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册第一章 1.1等腰三角形 同步测试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 101.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 14:47:52 | ||
图片预览

文档简介
2020-2021学年北师大版八年级数学下册第一章
1.1等腰三角形
同步测试题
(时间:100分钟 满分:100分)
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案填在下面的答题框内)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
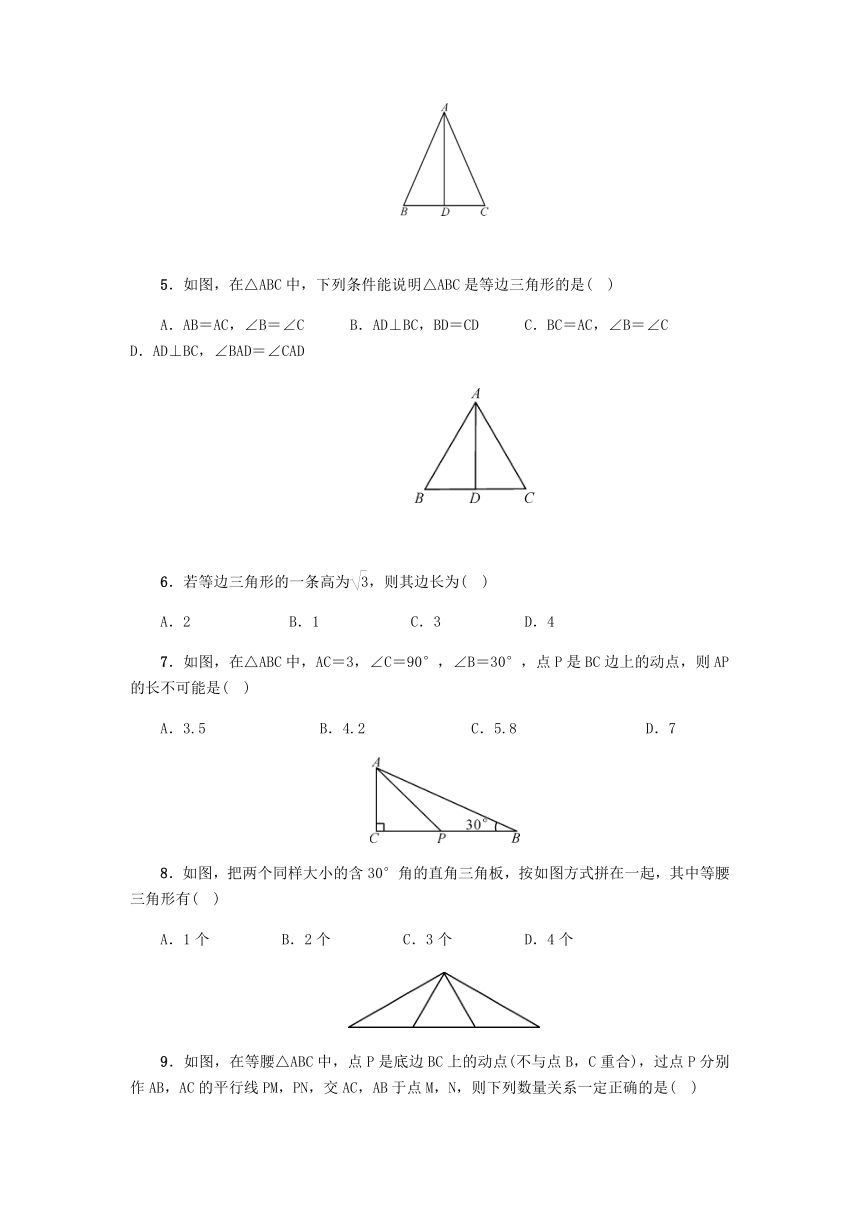
1.如图,在△ABC中,AB=AC,∠B=65°,则∠A的度数是(
)
A.70°
B.55°
C.50°
D.40°
2.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是(
)
A.76°
B.62°
C.42°
D.76°,62°或42°都可以
3.如图,直线l∥m∥n,等边△ABC的顶点B,C分别在直线n和m上,边BC与直线n所夹锐角为28°,则∠α的度数为(
)
A.28°
B.30°
C.32°
D.45°
4.如图,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是(
)
A.∠B=∠C
B.AD⊥BC
C.AD平分∠BAC
D.AB=2BD
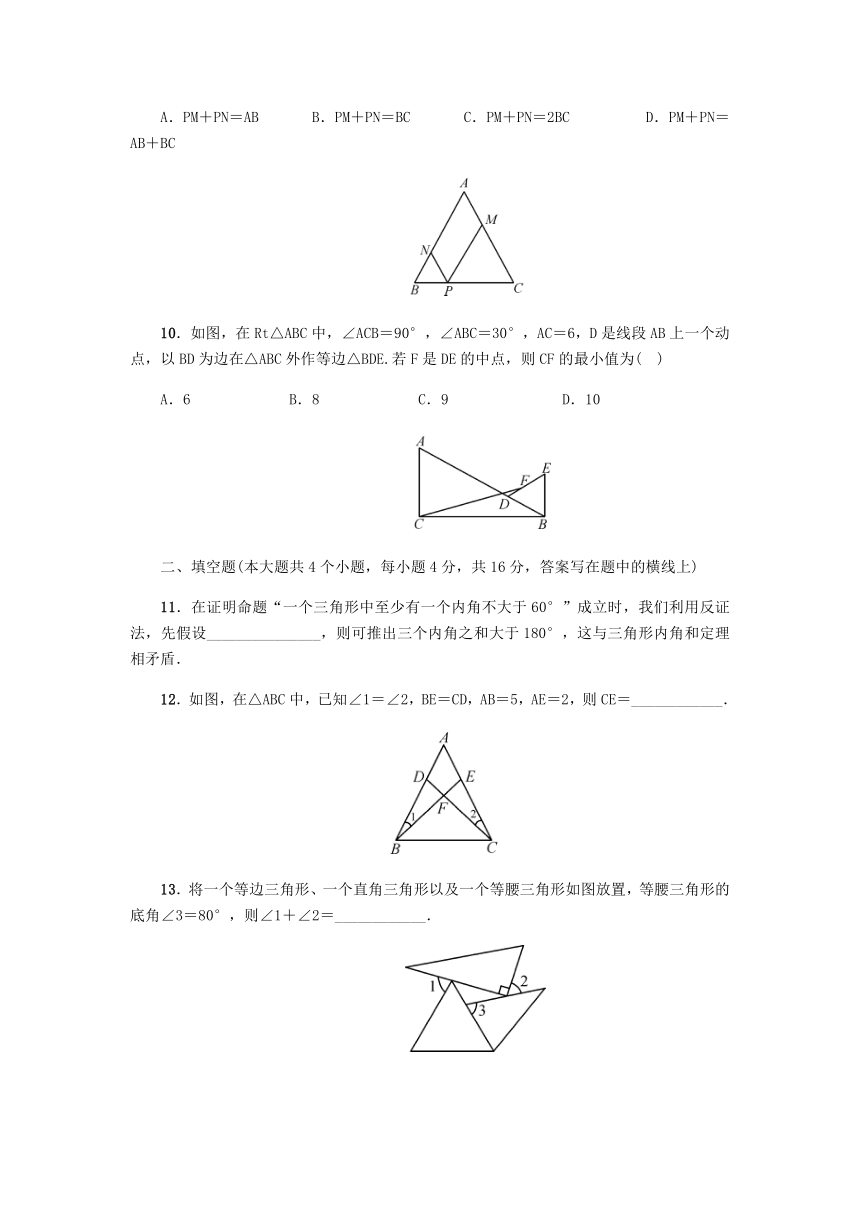
5.如图,在△ABC中,下列条件能说明△ABC是等边三角形的是(
)
A.AB=AC,∠B=∠C
B.AD⊥BC,BD=CD
C.BC=AC,∠B=∠C
D.AD⊥BC,∠BAD=∠CAD
6.若等边三角形的一条高为,则其边长为(
)
A.2
B.1
C.3
D.4
7.如图,在△ABC中,AC=3,∠C=90°,∠B=30°,点P是BC边上的动点,则AP的长不可能是(
)
A.3.5
B.4.2
C.5.8
D.7
8.如图,把两个同样大小的含30°角的直角三角板,按如图方式拼在一起,其中等腰三角形有(
)
A.1个
B.2个
C.3个
D.4个
9.如图,在等腰△ABC中,点P是底边BC上的动点(不与点B,C重合),过点P分别作AB,AC的平行线PM,PN,交AC,AB于点M,N,则下列数量关系一定正确的是(
)
A.PM+PN=AB
B.PM+PN=BC
C.PM+PN=2BC
D.PM+PN=AB+BC
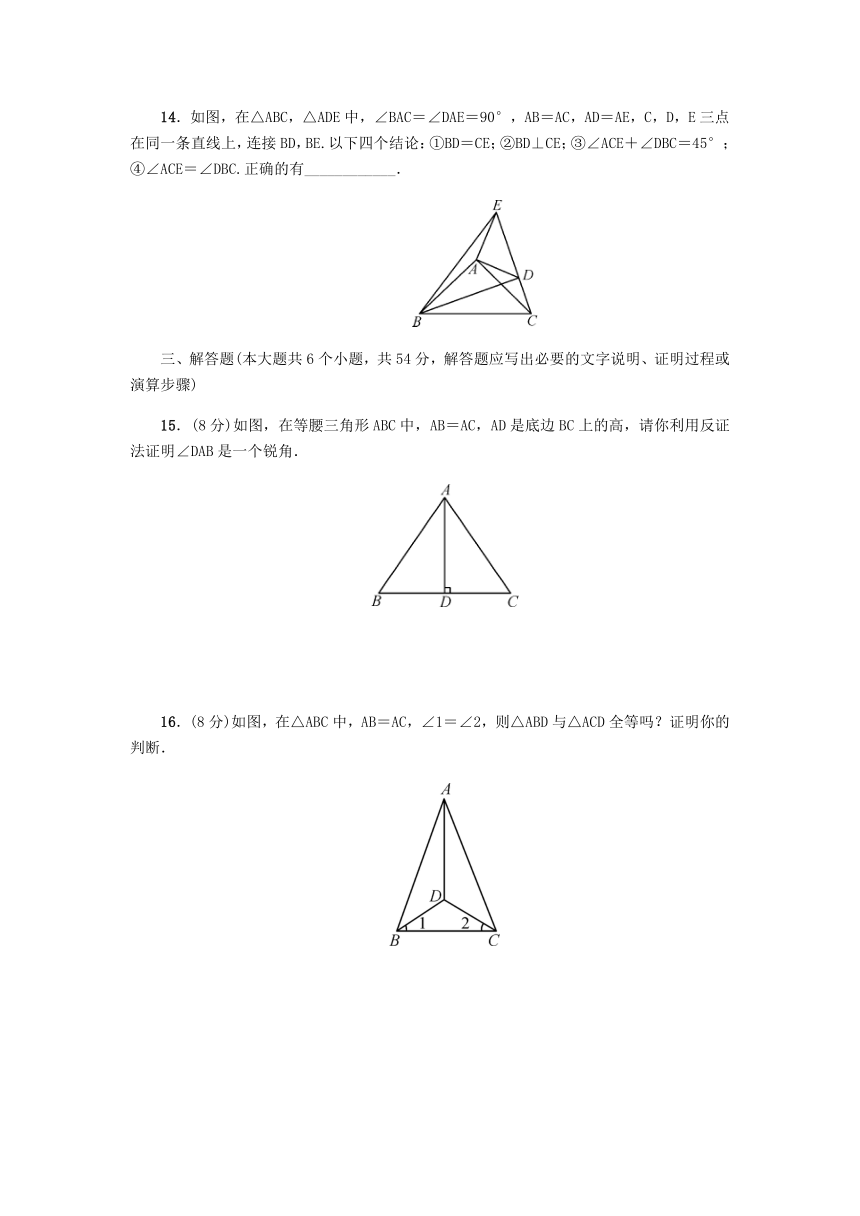
10.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=6,D是线段AB上一个动点,以BD为边在△ABC外作等边△BDE.若F是DE的中点,则CF的最小值为(
)
A.6
B.8
C.9
D.10
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.在证明命题“一个三角形中至少有一个内角不大于60°”成立时,我们利用反证法,先假设_______________,则可推出三个内角之和大于180°,这与三角形内角和定理相矛盾.
12.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE=____________.
13.将一个等边三角形、一个直角三角形以及一个等腰三角形如图放置,等腰三角形的底角∠3=80°,则∠1+∠2=____________.
14.如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠ACE=∠DBC.正确的有____________.
三、解答题(本大题共6个小题,共54分,解答题应写出必要的文字说明、证明过程或演算步骤)
15.(8分)如图,在等腰三角形ABC中,AB=AC,AD是底边BC上的高,请你利用反证法证明∠DAB是一个锐角.
16.(8分)如图,在△ABC中,AB=AC,∠1=∠2,则△ABD与△ACD全等吗?证明你的判断.
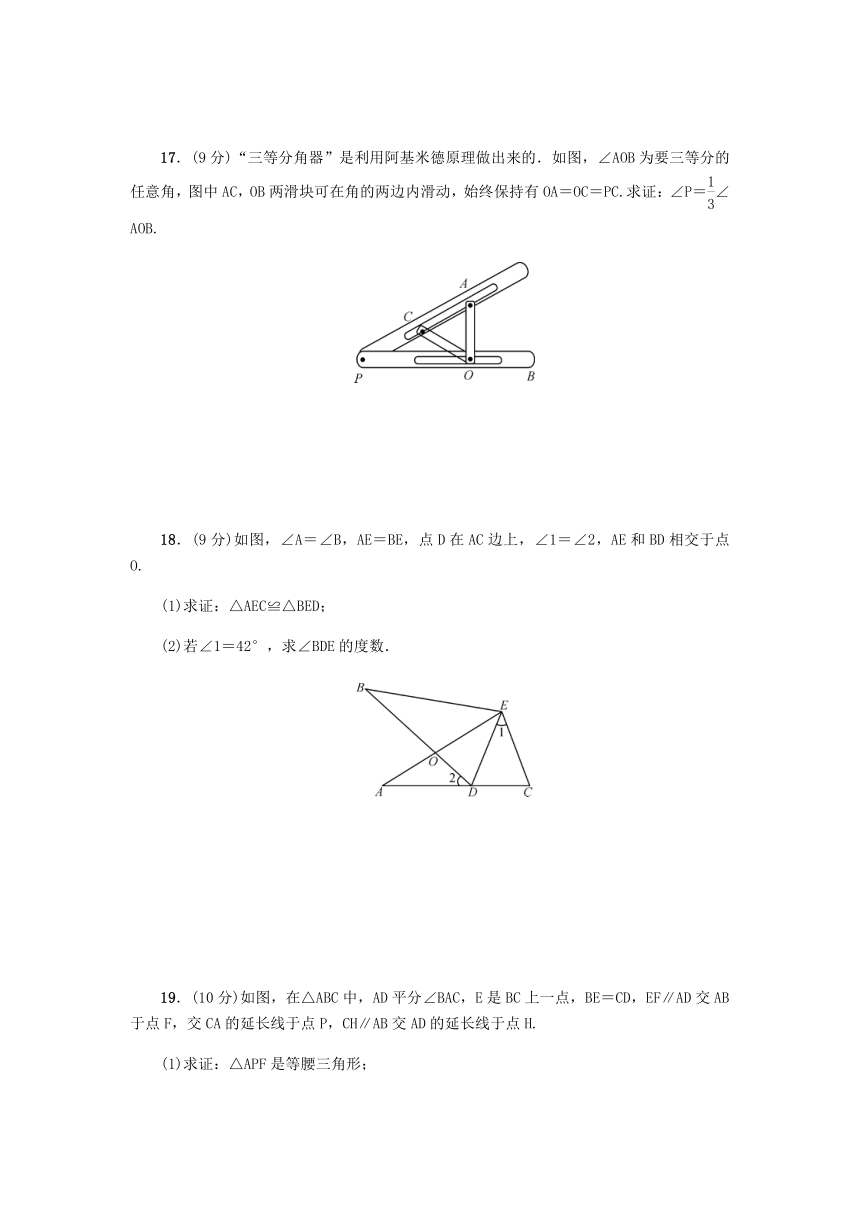
17.(9分)“三等分角器”是利用阿基米德原理做出来的.如图,∠AOB为要三等分的任意角,图中AC,OB两滑块可在角的两边内滑动,始终保持有OA=OC=PC.求证:∠P=∠AOB.
18.(9分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
19.(10分)如图,在△ABC中,AD平分∠BAC,E是BC上一点,BE=CD,EF∥AD交AB于点F,交CA的延长线于点P,CH∥AB交AD的延长线于点H.
(1)求证:△APF是等腰三角形;
(2)猜想AB与PC的大小有什么关系?证明你的猜想.
20.(10分)如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)求证:△ODE是等边三角形;
(2)线段BD,DE,EC三者有什么数量关系?写出你的判断过程;
(3)数学学习不但要能解决问题,还要善于提出问题.结合本题,在现有的图形上,请提出两个与“直角三角形”有关的问题.(只要提出问题,不需要解答)
参考答案
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案填在下面的答题框内)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
C
D
C
A
D
D
A
C
1.如图,在△ABC中,AB=AC,∠B=65°,则∠A的度数是(C)
A.70°
B.55°
C.50°
D.40°
2.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是(B)
A.76°
B.62°
C.42°
D.76°,62°或42°都可以
3.如图,直线l∥m∥n,等边△ABC的顶点B,C分别在直线n和m上,边BC与直线n所夹锐角为28°,则∠α的度数为(C)
A.28°
B.30°
C.32°
D.45°
4.如图,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是(D)
A.∠B=∠C
B.AD⊥BC
C.AD平分∠BAC
D.AB=2BD
5.如图,在△ABC中,下列条件能说明△ABC是等边三角形的是(C)
A.AB=AC,∠B=∠C
B.AD⊥BC,BD=CD
C.BC=AC,∠B=∠C
D.AD⊥BC,∠BAD=∠CAD
6.若等边三角形的一条高为,则其边长为(A)
A.2
B.1
C.3
D.4
7.如图,在△ABC中,AC=3,∠C=90°,∠B=30°,点P是BC边上的动点,则AP的长不可能是(D)
A.3.5
B.4.2
C.5.8
D.7
8.如图,把两个同样大小的含30°角的直角三角板,按如图方式拼在一起,其中等腰三角形有(D)
A.1个
B.2个
C.3个
D.4个
9.如图,在等腰△ABC中,点P是底边BC上的动点(不与点B,C重合),过点P分别作AB,AC的平行线PM,PN,交AC,AB于点M,N,则下列数量关系一定正确的是(A)
A.PM+PN=AB
B.PM+PN=BC
C.PM+PN=2BC
D.PM+PN=AB+BC
10.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=6,D是线段AB上一个动点,以BD为边在△ABC外作等边△BDE.若F是DE的中点,则CF的最小值为(C)
A.6
B.8
C.9
D.10
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.在证明命题“一个三角形中至少有一个内角不大于60°”成立时,我们利用反证法,先假设三角形的三个内角都大于60°,则可推出三个内角之和大于180°,这与三角形内角和定理相矛盾.
12.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE=3.
13.将一个等边三角形、一个直角三角形以及一个等腰三角形如图放置,等腰三角形的底角∠3=80°,则∠1+∠2=130°.
14.如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠ACE=∠DBC.正确的有①②③.
三、解答题(本大题共6个小题,共54分,解答题应写出必要的文字说明、证明过程或演算步骤)
15.(8分)如图,在等腰三角形ABC中,AB=AC,AD是底边BC上的高,请你利用反证法证明∠DAB是一个锐角.
解:假设∠DAB是钝角或直角,
∵AB=AC,AD是底边BC上的高,
∴∠BAC=2∠DAB.
∵∠DAB是钝角或直角,
∴2∠DAB≥180°,不符合三角形内角和定理.
∴假设不成立.
∴∠DAB是一个锐角.
16.(8分)如图,在△ABC中,AB=AC,∠1=∠2,则△ABD与△ACD全等吗?证明你的判断.
解:△ABD≌△ACD.证明如下:
∵AB=AC,∴∠ABC=∠ACB.
∵∠1=∠2,
∴BD=CD,∠ABC-∠1=∠ACB-∠2,即∠ABD=∠ACD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SAS).
17.(9分)“三等分角器”是利用阿基米德原理做出来的.如图,∠AOB为要三等分的任意角,图中AC,OB两滑块可在角的两边内滑动,始终保持有OA=OC=PC.求证:∠P=∠AOB.
证明:∵OC=PC,
∴∠P=∠COP.
∵OA=OC,
∴∠ACO=∠CAO.
∵∠ACO是△PCO的一个外角,
∴∠ACO=∠P+∠COP=2∠P.
∴∠CAO=∠ACO=2∠P.
∵∠AOB是△PAO的一个外角,
∴∠AOB=∠CAO+∠P=3∠P.
∴∠P=∠AOB.
18.(9分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
解:(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
∵∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO.
∴∠1+∠AED=∠BEO+∠AED,
即∠AEC=∠BED.
在△AEC和△BED中,
∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,∵EC=ED,∠1=42°,
∴∠C=∠EDC=69°.
∴∠BDE=∠C=69°.
19.(10分)如图,在△ABC中,AD平分∠BAC,E是BC上一点,BE=CD,EF∥AD交AB于点F,交CA的延长线于点P,CH∥AB交AD的延长线于点H.
(1)求证:△APF是等腰三角形;
(2)猜想AB与PC的大小有什么关系?证明你的猜想.
解:(1)证明:∵EF∥AD,∴∠BAD=∠AFP,∠CAD=∠P.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∴∠AFP=∠P.
∴AF=AP,即△APF是等腰三角形.
(2)AB=PC.
证明:∵CH∥AB,∴∠BCH=∠B,∠H=∠BAD,
∵EF∥AD,
∴∠BAD=∠BFE.
∴∠H=∠BFE.
在△CDH和△BEF中,
∴△CDH≌△BEF(AAS).
∴BF=CH.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∴∠CAD=∠H.
∴AC=CH.
∴AC=BF.
∵AB=AF+BF,PC=AP+AC,
∴AB=PC.
20.(10分)如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)求证:△ODE是等边三角形;
(2)线段BD,DE,EC三者有什么数量关系?写出你的判断过程;
(3)数学学习不但要能解决问题,还要善于提出问题.结合本题,在现有的图形上,请提出两个与“直角三角形”有关的问题.(只要提出问题,不需要解答)
解:(1)证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°.
∴△ODE是等边三角形.
(2)BD=DE=EC.
理由:∵OB平分∠ABC,且∠ABC=60°,
∴∠ABO=∠OBD=30°.
∵OD∥AB,
∴∠BOD=∠ABO=30°.
∴∠OBD=∠BOD.
∴DB=DO.
同理,EC=EO.
由(1)知,△ODE是等边三角形,
∴DE=OD=OE.
∴BD=DE=EC.
(3)答案不唯一,如:①连接AO,并延长交BC于点F,求证:△ABF是直角三角形;
②若等边△ABC的边长为1,求BC边上的高.
1.1等腰三角形
同步测试题
(时间:100分钟 满分:100分)
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案填在下面的答题框内)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
1.如图,在△ABC中,AB=AC,∠B=65°,则∠A的度数是(
)
A.70°
B.55°
C.50°
D.40°
2.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是(
)
A.76°
B.62°
C.42°
D.76°,62°或42°都可以
3.如图,直线l∥m∥n,等边△ABC的顶点B,C分别在直线n和m上,边BC与直线n所夹锐角为28°,则∠α的度数为(
)
A.28°
B.30°
C.32°
D.45°
4.如图,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是(
)
A.∠B=∠C
B.AD⊥BC
C.AD平分∠BAC
D.AB=2BD
5.如图,在△ABC中,下列条件能说明△ABC是等边三角形的是(
)
A.AB=AC,∠B=∠C
B.AD⊥BC,BD=CD
C.BC=AC,∠B=∠C
D.AD⊥BC,∠BAD=∠CAD
6.若等边三角形的一条高为,则其边长为(
)
A.2
B.1
C.3
D.4
7.如图,在△ABC中,AC=3,∠C=90°,∠B=30°,点P是BC边上的动点,则AP的长不可能是(
)
A.3.5
B.4.2
C.5.8
D.7
8.如图,把两个同样大小的含30°角的直角三角板,按如图方式拼在一起,其中等腰三角形有(
)
A.1个
B.2个
C.3个
D.4个
9.如图,在等腰△ABC中,点P是底边BC上的动点(不与点B,C重合),过点P分别作AB,AC的平行线PM,PN,交AC,AB于点M,N,则下列数量关系一定正确的是(
)
A.PM+PN=AB
B.PM+PN=BC
C.PM+PN=2BC
D.PM+PN=AB+BC
10.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=6,D是线段AB上一个动点,以BD为边在△ABC外作等边△BDE.若F是DE的中点,则CF的最小值为(
)
A.6
B.8
C.9
D.10
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.在证明命题“一个三角形中至少有一个内角不大于60°”成立时,我们利用反证法,先假设_______________,则可推出三个内角之和大于180°,这与三角形内角和定理相矛盾.
12.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE=____________.
13.将一个等边三角形、一个直角三角形以及一个等腰三角形如图放置,等腰三角形的底角∠3=80°,则∠1+∠2=____________.
14.如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠ACE=∠DBC.正确的有____________.
三、解答题(本大题共6个小题,共54分,解答题应写出必要的文字说明、证明过程或演算步骤)
15.(8分)如图,在等腰三角形ABC中,AB=AC,AD是底边BC上的高,请你利用反证法证明∠DAB是一个锐角.
16.(8分)如图,在△ABC中,AB=AC,∠1=∠2,则△ABD与△ACD全等吗?证明你的判断.
17.(9分)“三等分角器”是利用阿基米德原理做出来的.如图,∠AOB为要三等分的任意角,图中AC,OB两滑块可在角的两边内滑动,始终保持有OA=OC=PC.求证:∠P=∠AOB.
18.(9分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
19.(10分)如图,在△ABC中,AD平分∠BAC,E是BC上一点,BE=CD,EF∥AD交AB于点F,交CA的延长线于点P,CH∥AB交AD的延长线于点H.
(1)求证:△APF是等腰三角形;
(2)猜想AB与PC的大小有什么关系?证明你的猜想.
20.(10分)如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)求证:△ODE是等边三角形;
(2)线段BD,DE,EC三者有什么数量关系?写出你的判断过程;
(3)数学学习不但要能解决问题,还要善于提出问题.结合本题,在现有的图形上,请提出两个与“直角三角形”有关的问题.(只要提出问题,不需要解答)
参考答案
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案填在下面的答题框内)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
C
D
C
A
D
D
A
C
1.如图,在△ABC中,AB=AC,∠B=65°,则∠A的度数是(C)
A.70°
B.55°
C.50°
D.40°
2.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是(B)
A.76°
B.62°
C.42°
D.76°,62°或42°都可以
3.如图,直线l∥m∥n,等边△ABC的顶点B,C分别在直线n和m上,边BC与直线n所夹锐角为28°,则∠α的度数为(C)
A.28°
B.30°
C.32°
D.45°
4.如图,在△ABC中,AB=AC,D是BC的中点,下列结论中不正确的是(D)
A.∠B=∠C
B.AD⊥BC
C.AD平分∠BAC
D.AB=2BD
5.如图,在△ABC中,下列条件能说明△ABC是等边三角形的是(C)
A.AB=AC,∠B=∠C
B.AD⊥BC,BD=CD
C.BC=AC,∠B=∠C
D.AD⊥BC,∠BAD=∠CAD
6.若等边三角形的一条高为,则其边长为(A)
A.2
B.1
C.3
D.4
7.如图,在△ABC中,AC=3,∠C=90°,∠B=30°,点P是BC边上的动点,则AP的长不可能是(D)
A.3.5
B.4.2
C.5.8
D.7
8.如图,把两个同样大小的含30°角的直角三角板,按如图方式拼在一起,其中等腰三角形有(D)
A.1个
B.2个
C.3个
D.4个
9.如图,在等腰△ABC中,点P是底边BC上的动点(不与点B,C重合),过点P分别作AB,AC的平行线PM,PN,交AC,AB于点M,N,则下列数量关系一定正确的是(A)
A.PM+PN=AB
B.PM+PN=BC
C.PM+PN=2BC
D.PM+PN=AB+BC
10.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=6,D是线段AB上一个动点,以BD为边在△ABC外作等边△BDE.若F是DE的中点,则CF的最小值为(C)
A.6
B.8
C.9
D.10
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.在证明命题“一个三角形中至少有一个内角不大于60°”成立时,我们利用反证法,先假设三角形的三个内角都大于60°,则可推出三个内角之和大于180°,这与三角形内角和定理相矛盾.
12.如图,在△ABC中,已知∠1=∠2,BE=CD,AB=5,AE=2,则CE=3.
13.将一个等边三角形、一个直角三角形以及一个等腰三角形如图放置,等腰三角形的底角∠3=80°,则∠1+∠2=130°.
14.如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠ACE=∠DBC.正确的有①②③.
三、解答题(本大题共6个小题,共54分,解答题应写出必要的文字说明、证明过程或演算步骤)
15.(8分)如图,在等腰三角形ABC中,AB=AC,AD是底边BC上的高,请你利用反证法证明∠DAB是一个锐角.
解:假设∠DAB是钝角或直角,
∵AB=AC,AD是底边BC上的高,
∴∠BAC=2∠DAB.
∵∠DAB是钝角或直角,
∴2∠DAB≥180°,不符合三角形内角和定理.
∴假设不成立.
∴∠DAB是一个锐角.
16.(8分)如图,在△ABC中,AB=AC,∠1=∠2,则△ABD与△ACD全等吗?证明你的判断.
解:△ABD≌△ACD.证明如下:
∵AB=AC,∴∠ABC=∠ACB.
∵∠1=∠2,
∴BD=CD,∠ABC-∠1=∠ACB-∠2,即∠ABD=∠ACD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SAS).
17.(9分)“三等分角器”是利用阿基米德原理做出来的.如图,∠AOB为要三等分的任意角,图中AC,OB两滑块可在角的两边内滑动,始终保持有OA=OC=PC.求证:∠P=∠AOB.
证明:∵OC=PC,
∴∠P=∠COP.
∵OA=OC,
∴∠ACO=∠CAO.
∵∠ACO是△PCO的一个外角,
∴∠ACO=∠P+∠COP=2∠P.
∴∠CAO=∠ACO=2∠P.
∵∠AOB是△PAO的一个外角,
∴∠AOB=∠CAO+∠P=3∠P.
∴∠P=∠AOB.
18.(9分)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
解:(1)证明:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
∵∠A=∠B,
∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO.
∴∠1+∠AED=∠BEO+∠AED,
即∠AEC=∠BED.
在△AEC和△BED中,
∴△AEC≌△BED(ASA).
(2)∵△AEC≌△BED,
∴EC=ED,∠C=∠BDE.
在△EDC中,∵EC=ED,∠1=42°,
∴∠C=∠EDC=69°.
∴∠BDE=∠C=69°.
19.(10分)如图,在△ABC中,AD平分∠BAC,E是BC上一点,BE=CD,EF∥AD交AB于点F,交CA的延长线于点P,CH∥AB交AD的延长线于点H.
(1)求证:△APF是等腰三角形;
(2)猜想AB与PC的大小有什么关系?证明你的猜想.
解:(1)证明:∵EF∥AD,∴∠BAD=∠AFP,∠CAD=∠P.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∴∠AFP=∠P.
∴AF=AP,即△APF是等腰三角形.
(2)AB=PC.
证明:∵CH∥AB,∴∠BCH=∠B,∠H=∠BAD,
∵EF∥AD,
∴∠BAD=∠BFE.
∴∠H=∠BFE.
在△CDH和△BEF中,
∴△CDH≌△BEF(AAS).
∴BF=CH.
∵AD平分∠BAC,∴∠BAD=∠CAD.
∴∠CAD=∠H.
∴AC=CH.
∴AC=BF.
∵AB=AF+BF,PC=AP+AC,
∴AB=PC.
20.(10分)如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)求证:△ODE是等边三角形;
(2)线段BD,DE,EC三者有什么数量关系?写出你的判断过程;
(3)数学学习不但要能解决问题,还要善于提出问题.结合本题,在现有的图形上,请提出两个与“直角三角形”有关的问题.(只要提出问题,不需要解答)
解:(1)证明:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵OD∥AB,OE∥AC,
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°.
∴△ODE是等边三角形.
(2)BD=DE=EC.
理由:∵OB平分∠ABC,且∠ABC=60°,
∴∠ABO=∠OBD=30°.
∵OD∥AB,
∴∠BOD=∠ABO=30°.
∴∠OBD=∠BOD.
∴DB=DO.
同理,EC=EO.
由(1)知,△ODE是等边三角形,
∴DE=OD=OE.
∴BD=DE=EC.
(3)答案不唯一,如:①连接AO,并延长交BC于点F,求证:△ABF是直角三角形;
②若等边△ABC的边长为1,求BC边上的高.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
