3.5 洛伦兹力 期末复习学案Word版含解析
文档属性
| 名称 | 3.5 洛伦兹力 期末复习学案Word版含解析 |  | |
| 格式 | doc | ||
| 文件大小 | 807.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-15 14:56:12 | ||
图片预览


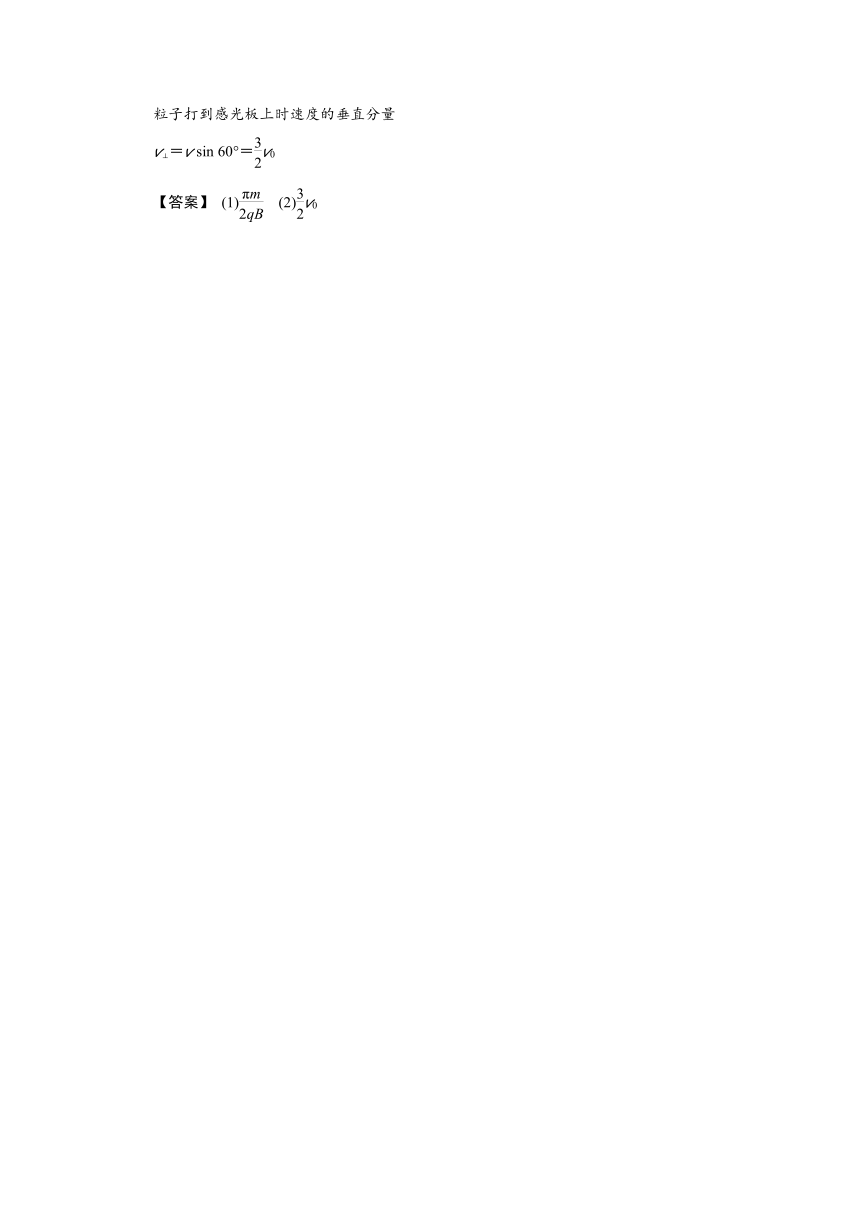


文档简介
洛伦兹力
1.洛伦兹力是指磁场对运动电荷的作用力。
2.如果一个电荷的电量为q,速度为v且与磁场方向垂直,则该电荷受到的洛伦兹力F洛=qvB,如果v的方向与B的方向成θ角,则F洛=qvB sinθ(当B// v时:电荷不受洛伦兹力;当B⊥v时:电荷所受的洛伦兹力最大)。
3.洛伦兹力始终与电荷运动方向垂直,只改变速度的方向,而不改变速度的大小,所以洛伦兹力对运动的电荷不做功。
4.运动方向与磁场方向平行时,不受洛伦兹力作用,做匀速直线运动。
5. 运动方向与磁场方向垂直时,做匀速圆周运动,洛伦兹力提供向心力,运动半径 r=,运动周期: T=。
6.运动方向与磁场方向既不平行也不垂直时,做半径相等、螺距相等的螺旋运动 。
例1 两块金属板a、b平行放置,板间存在与匀强电场正交的匀强磁场,假设电场、磁场只存在于两板间的空间区域。一束电子以一定的初速度v0从两极板中间,沿垂直于电场、磁场的方向射入场中,无偏转地通过场区,如图所示,已知板长l=10 cm,两板间距d=3.0 cm,两板间电势差U=150 V,v0=2.0×107 m/s。
(1)求磁感应强度B的大小;
(2)若撤去磁场,求电子穿过电场时偏离入射方向的距离,以及电子通过场区后动能的增加量(电子所带电荷量的大小与其质量之比=1.76×1011 C/kg,电子带电荷量的大小e=1.60×10-19 C)。
【解析】 (1)电子进入正交的电、磁场不发生偏转,则满足
Bev0=e,B==2.5×10-4 T
(2)设电子通过场区偏转的距离为y1
y1=at2=··=1.1×10-2 m
ΔEk=eEy1=ey1=8.8×10-18 J=55 eV
【答案】 (1)2.5×10-4 T (2)55 eV
例2 如图所示,在半径R=的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度为B,圆形区域右侧有一竖直感光板,圆弧顶点P有一速率为v0的带正电的粒子平行于纸面进入磁场,已知粒子的质量为m,电荷量为q,粒子重力不计。
(1)若粒子对准圆心射入,求它在磁场中运动的时间;
(2)若粒子对准圆心射入,且速率为v0,求它打到感光板上时速度的垂直分量。
【解析】 (1)设带电粒子进入磁场中做匀速圆周运动的轨迹半径为r,由牛顿第二定律得
Bqv0=m
所以r==R
带电粒子在磁场中的运动轨迹为四分之一圆周,轨迹对应的圆心角为。
则它在磁场中运动的时间t==
(2)由(1)知,当v=v0时,带电粒子在磁场中运动的轨迹半径为R,其运动轨迹如图所示。
由几何关系可知∠PO2O=∠OO2A=30°
所以带电粒子离开磁场时偏转角为60°
粒子打到感光板上时速度的垂直分量
v⊥=v sin 60°=v0
【答案】 (1) (2)v0
1.下列关于洛伦兹力的说法中,正确的是( )
A.只要速度大小相同,所受洛伦兹力就相同
B.如果把+q改为-q,且速度反向,大小不变,则洛伦兹力的大小、方向均不变
C.洛伦兹力方向一定与电荷速度方向垂直,磁场方向一定与电荷运动方向垂直
D.粒子在只受到洛伦兹力作用下运动的动能、速度均不变
2.如图所示,在竖直绝缘的平台上,一个带正电的小球以水平速度v0抛出,落在地面上的A点,若加一垂直纸面向里的匀强磁场,则小球的落点( )
A.仍在A点 B.在A点左侧
C.在A点右侧 D.无法确定
3.如图,半径为R的圆是一圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B,方向垂直于纸面向外。一电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域,射入点与ab的距离为。已知粒子射出磁场与射入磁场时运动方向间的夹角为60°,则粒子的速率为(不计重力)( )
A. B.
C. D.
4.(多选)如图两个初速度大小相同的同种离子a和b,从O点沿垂直磁场方向进入匀强磁场,最后打到屏P上,不计重力,下列说法正确的有( )
A.a、b均带正电
B.a在磁场中飞行的时间比b的短
C.a在磁场中飞行的路程比b的短
D.a在P上的落点与O点的距离比b的近
5.(多选)一个带正电的小球沿光滑绝缘的水平桌面向右运动,小球离开桌面后进入一水平向里的匀强磁场,已知速度方向垂直于磁场方向,如图所示,小球飞离桌面后落到地板上,设飞行时间为t1,水平射程为x1,着地速度为v1,撤去磁场,其余的条件不变,小球飞行时间为t2,水平射程为x2,着地速度为v2,则下列论述正确的是( )
A.x1>x2
B.t1>t2
C.v1和v2大小相等
D.v1和v2方向相同
6.质量和电荷量都相等的带电粒子M和N,以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,下列表述正确的是( )
A.M带负电,N带正电
B. M的速度率小于N的速率
C.洛伦兹力对M、N做正功
D.M的运行时间大于N的运行时间
7.如图所示,一轨道由两等长的光滑斜面AB和BC组成,两斜面在B处用一光滑小圆弧相连接,BA、BC关于竖直线BD对称且BD右侧存在垂直纸面向里的匀强磁场,B处可认为处在磁场中,P是BC的中点,一带电小球从A点由静止释放后能沿轨道来回运动,C点为小球在BD右侧运动的最高点,则下列说法正确的是( )
A.C点与A点不在同一水平线上
B.小球向右或向左滑过B点时,对轨道压力相等
C.小球向上或向下滑过P点时,其所受洛伦兹力相同
D.小球从A到B的时间是从C到P时间的倍
8.如图所示,在加有匀强磁场的区域中,一垂直于磁场方向射入的带电粒子轨迹如图所示,由于带电粒子与沿途的气体分子发生碰撞,带电粒子的能量逐渐减小,从图中可以看出( )
A.带电粒子带正电,是从B点射入的
B.带电粒子带负电,是从B点射入的
C.带电粒子带负电,是从A点射入的
D.带电粒子带正电,是从A点射入的
9.如图,空间有一圆柱形匀强磁场区域,该区域的横截面的半径为R,磁场方向垂直于横截面。一质量为m、电荷量为q(q>0)的粒子以速率v0沿横截面的某直径射入磁场,离开磁场时速度方向偏离入射方向60°。不计重力,该磁场的磁感应强度大小为( )
A. B.
C. D.
10.(多选)如图所示,ABC为竖直平面内的光滑绝缘轨道,其中AB为倾斜直轨道,BC为与AB相切的圆形轨道,并且圆形轨道处在匀强磁场中,磁场方向垂直纸面向里,质量相同的甲、乙、丙三个小球中,甲球带正电,乙球带负电,丙球不带电,现将三个小球在轨道AB上分别从不同高度处由静止释放,都恰好通过圆形轨道的最高点,则( )
A.经过最高点时,三个小球的速度相等
B.经过最高点时,甲球的速度最小
C.甲球的释放位置比乙球的高
D.运动过程中三个小球的机械能均保持不变
11.如图所示,在x轴上方有匀强磁场B,一个质量为m,带电荷量为-q的粒子,以速度v从O点射入磁场,θ角已知,粒子重力不计,求:
(1)粒子在磁场中运动时间为多少?
(2)粒子离开磁场时的位置到O点的距离为多少?
12.如图所示,分布在半径为r的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里,电荷量为q、质量为m的带正电的粒子从磁场边缘A点沿圆的半径AO方向射入磁场,离开磁场时速度方向偏转了60°角(重力忽略不计)。试确定:
(1)粒子做圆周运动的半径;
(2)粒子的入射速度;
(3)粒子在磁场中运动的时间。
13.如图所示,以MN为界的两匀强磁场,磁感应强度B1=2B2,方向垂直纸面向里,现有一质量为m、带电荷量为q的正粒子,从O点沿图示方向进入B1中。
(1)试画出此粒子的运动轨迹;
(2)求经过多长时间粒子重新回到O点?
1.带电粒子垂直于匀强磁场方向运动时,会受到洛伦兹力的作用。下列表述正确的是( )
A.洛伦兹力对带电粒子做功
B.洛伦兹力不改变带电粒子的动能
C.洛伦兹力的大小与速度无关
D.洛伦兹力不改变带电粒子的速度方向
2.(2015·新课标)两相邻匀强磁场区域的磁感应强度大小不同、方向平行。一速度方向与磁感应强度方向垂直的带电粒子(不计重力),从较强磁场区域进入到较弱磁场区域后,粒子的( )
A.轨道半径减小,角速度增大
B.轨道半径减小,角速度减小
C.轨道半径增大,角速度增大
D.轨道半径增大,角速度减小
3.两个质量相同、所带电荷量相等的带电粒子a、b,以不同的速率对准圆心O沿着AO方向射入圆形匀强磁场区域,其运动轨迹如图。若不计粒子的重力,则下列说法正确的是( )
A.a粒子带正电,b粒子带负电
B.a粒子在磁场中所受洛伦兹力较大
C.b粒子动能较大
D.b粒子在磁场中运动时间较长
4.(多选)如图所示,在圆形区域里,有匀强磁场,方向如图所示。有一束速率各不相同的质子自A点沿半径方向射入磁场,这些质子在磁场中( )
A.运动时间越长的,其轨迹所对应的圆心角越大
B.运动时间越长的,其轨迹越长
C.运动时间越短的射出磁场时,速率越小
D.运动时间越短时,射出磁场时,速度方向偏转越小
5.如右图所示,带负电的粒子以速度v从粒子源P处射出,若图中匀强磁场范围足够大(方向垂直纸面),则带电粒子的可能轨迹是( )
A.a B.b
C.c D.d
6.(多选)如图所示,空间存在水平向右的匀强电场和垂直于纸面向外的匀强磁场。一个带正电的小球套在竖直绝缘细杆上,与细杆间的动摩擦因数为μ,由静止释放后小球将向下运动,设细杆足够长,则( )
A.小球将做匀加速直线运动
B.小球的加速度先增大后减小
C.小球最终将做匀速运动
D.小球将做加速度一直减小的加速运动
7.(多选)如图所示是粒子速度选择器的原理图,如果粒子所具有的速率v = ,那么( )
A.带正电粒子必须沿ab方向从左侧进入场区,才能沿直线通过
B.带负电粒子必须沿ba方向从右侧进入场区,才能沿直线通过
C.不论粒子电性如何,沿ab方向从左侧进入场区,都能沿直线通过
D.不论粒子电性如何,沿ba方向从右侧进入场区,都能沿直线通过
8.长为L的水平板间,有垂直纸面向内的匀强磁场,如图所示,磁感应强度为B,板间距离也为L,板不带电,现有质量为m,电荷量为q的带正电粒子(不计重力),从左边极板间中点处垂直磁感线以速度v水平射入磁场,欲使粒子打在极板上,可采用的办法是( )
A.使粒子的速度v<
B.使粒子的速度v>
C.使粒子的速度v>
D.使粒子的速度9.在图中虚线所围的区域内,存在电场强度为E的匀强电场和磁感应强度为B的匀强磁场。已知从左方水平射入的电子,穿过这区域时未发生偏转,设重力可以忽略不计,则在这区域中的E和B的方向不可能是( )
A.E和B都沿水平方向,并与电子运动的方向相同
B.E和B都沿水平方向,并与电子运动的方向相反
C.E竖直向上,B垂直纸面向外
D.E竖直向上,B垂直纸面向里
10.如图所示,带正电的小球用丝线悬挂着,在水平匀强磁场中摆动,摆动平面与磁场垂直,如图所示,图中C点为小球运动的最低点,小球向右运动和向左运动通过C点时,以下说法中正确
的是( )
A.受到的洛伦兹力相同
B.悬线对摆球的拉力相等
C.具有相同的动能
D.具有相同的速度
11.如图所示,质量为m的带正电小球能沿着竖直的绝缘墙竖直下滑,磁感应强度为B的匀强磁场方向水平,并与小球运动方向垂直。若小球带电荷量为q,球与墙间的动摩擦因数为μ,求小球下滑的最大速度和最大加速度。
12.质量为m,电荷量为q的粒子,以初速度v0垂直进入磁感应强度为B、宽度为L的匀强磁场区域,如图所示。求:
(1)带电粒子的运动轨迹及运动性质;
(2)带电粒子运动的轨道半径;
(3)带电粒子离开磁场电的速率;
(4)带电粒子离开磁场时的偏转角θ;
(5)带电粒子在磁场中的运动时间t;
(6)带电粒子离开磁场时偏转的侧位移。
13.如图所示,在x轴的上方(y>0的空间内)存在着垂直于纸面向里、磁感应强度为B的匀强磁场,一个不计重力的带正电粒子从坐标原点O处以速度v进入磁场,粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成45°角,若粒子的质量为m,电荷量为q,求:
(1)该粒子在磁场中做圆周运动的轨道半径;
(2)该粒子在磁场中运动的时间;
(3)该粒子射出磁场的位置坐标。
洛伦兹力
课堂练习
1.B 2.C 3.B 4.AD 5.ABC 6.A 7.D 8.B 9.A 10.CD
11.【答案】(1)t= (2)s=
【解析】(1)粒子做圆周运动的圆心一定在过O点且与速度v垂直的一条直线上,则有 r=,T=,粒子做圆周运动的圆心角(2π-2θ),所用时间t=T=。
(2)粒子离开磁场的位置与入射点的距离即为弦长:s=2rsin θ=。
12.【答案】(1)R=r (2)v= (3)t=
【解析】(1)设粒子做匀速圆周运动的半径为R,如图所示。sin ∠AOD==,所以∠AOD=120°,则三角形ADO′是等边三角形,故R=r。
(2)设洛伦兹力提供向心力:F洛=, 即qvB=,所以v=。
(3)由图知,粒子在磁场中的运动方向偏转了60°角,所以粒子完成了T个圆周运动,根据线速度与周期的关系v=,得T=。 粒子在磁场中的运动时间t=T=。
13.【答案】(1) (2)
【解析】(1)设粒子在磁场B1和B2中做圆周运动的半径为r1、r2,则r1=,r2=,由题意B1=2B2,得r1∶r2=1∶2,根据左手定则判断可以知道,粒子在磁场B1中沿逆时针方向旋转,在磁场B2中沿顺时针方向旋转,则轨迹图如上图。
(2)粒子在磁场B1中运动的时间t1=T1=, 粒子在磁场B2中运动的时间t2=T2=, 则t=t1+t2=。
课后练习
1.B 2.D 3.C 4.AD 5.B 6.BC 7.AC 8.D
9.D 10.C
11.【答案】,g
【解析】小球静止时只受重力,则加速度为g,下滑后,小球受到洛伦兹力、重力、支持力及摩擦力的作用,洛伦兹力水平向左,摩擦力竖直向上,小球向下做加速运动,速度越大,洛伦兹力越大,则摩擦力越大,加速度越小,当加速度等于零时,速度最大,则mg=μqvB,得v=。 此后小球做匀速直线运动,加速度为0,故开始时小球的加速度最大:a=g。
12.【答案】(1)见解析 (2) (2)v0
(3)arcsin (5) (6)(1-cos θ)
【解析】(1)粒子在磁场中受到洛伦兹力作用,力与速度始终垂直,故粒子做匀速圆周运动,轨迹是圆周。如图:
(2)由qv0B=m 得R=。
(3)粒子在磁场中只受到洛伦兹力作用,只改变速度方向,不改变大小,故离开磁场时速率仍为初速度大小v0。
(4)由几何关系可知:sin θ==。
(5)在磁场中的运动时间t==。
(6)y=R(1-cos θ)=(1-cos θ)。
13.【答案】(1) (2) (3)
【解析】(1)设粒子在磁场中做圆周运动的半径为R,由洛伦兹力和牛顿第二定律,有:qvB=,所以R=。
(2)粒子在磁场中运动对应的圆心角为270°, 又T=,所以t=T=。
(3)粒子离开磁场的位置,由几何关系得x=R,又R=,所以x=。 所以粒子射出磁场的位置坐标为。
1.洛伦兹力是指磁场对运动电荷的作用力。
2.如果一个电荷的电量为q,速度为v且与磁场方向垂直,则该电荷受到的洛伦兹力F洛=qvB,如果v的方向与B的方向成θ角,则F洛=qvB sinθ(当B// v时:电荷不受洛伦兹力;当B⊥v时:电荷所受的洛伦兹力最大)。
3.洛伦兹力始终与电荷运动方向垂直,只改变速度的方向,而不改变速度的大小,所以洛伦兹力对运动的电荷不做功。
4.运动方向与磁场方向平行时,不受洛伦兹力作用,做匀速直线运动。
5. 运动方向与磁场方向垂直时,做匀速圆周运动,洛伦兹力提供向心力,运动半径 r=,运动周期: T=。
6.运动方向与磁场方向既不平行也不垂直时,做半径相等、螺距相等的螺旋运动 。
例1 两块金属板a、b平行放置,板间存在与匀强电场正交的匀强磁场,假设电场、磁场只存在于两板间的空间区域。一束电子以一定的初速度v0从两极板中间,沿垂直于电场、磁场的方向射入场中,无偏转地通过场区,如图所示,已知板长l=10 cm,两板间距d=3.0 cm,两板间电势差U=150 V,v0=2.0×107 m/s。
(1)求磁感应强度B的大小;
(2)若撤去磁场,求电子穿过电场时偏离入射方向的距离,以及电子通过场区后动能的增加量(电子所带电荷量的大小与其质量之比=1.76×1011 C/kg,电子带电荷量的大小e=1.60×10-19 C)。
【解析】 (1)电子进入正交的电、磁场不发生偏转,则满足
Bev0=e,B==2.5×10-4 T
(2)设电子通过场区偏转的距离为y1
y1=at2=··=1.1×10-2 m
ΔEk=eEy1=ey1=8.8×10-18 J=55 eV
【答案】 (1)2.5×10-4 T (2)55 eV
例2 如图所示,在半径R=的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度为B,圆形区域右侧有一竖直感光板,圆弧顶点P有一速率为v0的带正电的粒子平行于纸面进入磁场,已知粒子的质量为m,电荷量为q,粒子重力不计。
(1)若粒子对准圆心射入,求它在磁场中运动的时间;
(2)若粒子对准圆心射入,且速率为v0,求它打到感光板上时速度的垂直分量。
【解析】 (1)设带电粒子进入磁场中做匀速圆周运动的轨迹半径为r,由牛顿第二定律得
Bqv0=m
所以r==R
带电粒子在磁场中的运动轨迹为四分之一圆周,轨迹对应的圆心角为。
则它在磁场中运动的时间t==
(2)由(1)知,当v=v0时,带电粒子在磁场中运动的轨迹半径为R,其运动轨迹如图所示。
由几何关系可知∠PO2O=∠OO2A=30°
所以带电粒子离开磁场时偏转角为60°
粒子打到感光板上时速度的垂直分量
v⊥=v sin 60°=v0
【答案】 (1) (2)v0
1.下列关于洛伦兹力的说法中,正确的是( )
A.只要速度大小相同,所受洛伦兹力就相同
B.如果把+q改为-q,且速度反向,大小不变,则洛伦兹力的大小、方向均不变
C.洛伦兹力方向一定与电荷速度方向垂直,磁场方向一定与电荷运动方向垂直
D.粒子在只受到洛伦兹力作用下运动的动能、速度均不变
2.如图所示,在竖直绝缘的平台上,一个带正电的小球以水平速度v0抛出,落在地面上的A点,若加一垂直纸面向里的匀强磁场,则小球的落点( )
A.仍在A点 B.在A点左侧
C.在A点右侧 D.无法确定
3.如图,半径为R的圆是一圆柱形匀强磁场区域的横截面(纸面),磁感应强度大小为B,方向垂直于纸面向外。一电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域,射入点与ab的距离为。已知粒子射出磁场与射入磁场时运动方向间的夹角为60°,则粒子的速率为(不计重力)( )
A. B.
C. D.
4.(多选)如图两个初速度大小相同的同种离子a和b,从O点沿垂直磁场方向进入匀强磁场,最后打到屏P上,不计重力,下列说法正确的有( )
A.a、b均带正电
B.a在磁场中飞行的时间比b的短
C.a在磁场中飞行的路程比b的短
D.a在P上的落点与O点的距离比b的近
5.(多选)一个带正电的小球沿光滑绝缘的水平桌面向右运动,小球离开桌面后进入一水平向里的匀强磁场,已知速度方向垂直于磁场方向,如图所示,小球飞离桌面后落到地板上,设飞行时间为t1,水平射程为x1,着地速度为v1,撤去磁场,其余的条件不变,小球飞行时间为t2,水平射程为x2,着地速度为v2,则下列论述正确的是( )
A.x1>x2
B.t1>t2
C.v1和v2大小相等
D.v1和v2方向相同
6.质量和电荷量都相等的带电粒子M和N,以不同的速率经小孔S垂直进入匀强磁场,运行的半圆轨迹如图中虚线所示,下列表述正确的是( )
A.M带负电,N带正电
B. M的速度率小于N的速率
C.洛伦兹力对M、N做正功
D.M的运行时间大于N的运行时间
7.如图所示,一轨道由两等长的光滑斜面AB和BC组成,两斜面在B处用一光滑小圆弧相连接,BA、BC关于竖直线BD对称且BD右侧存在垂直纸面向里的匀强磁场,B处可认为处在磁场中,P是BC的中点,一带电小球从A点由静止释放后能沿轨道来回运动,C点为小球在BD右侧运动的最高点,则下列说法正确的是( )
A.C点与A点不在同一水平线上
B.小球向右或向左滑过B点时,对轨道压力相等
C.小球向上或向下滑过P点时,其所受洛伦兹力相同
D.小球从A到B的时间是从C到P时间的倍
8.如图所示,在加有匀强磁场的区域中,一垂直于磁场方向射入的带电粒子轨迹如图所示,由于带电粒子与沿途的气体分子发生碰撞,带电粒子的能量逐渐减小,从图中可以看出( )
A.带电粒子带正电,是从B点射入的
B.带电粒子带负电,是从B点射入的
C.带电粒子带负电,是从A点射入的
D.带电粒子带正电,是从A点射入的
9.如图,空间有一圆柱形匀强磁场区域,该区域的横截面的半径为R,磁场方向垂直于横截面。一质量为m、电荷量为q(q>0)的粒子以速率v0沿横截面的某直径射入磁场,离开磁场时速度方向偏离入射方向60°。不计重力,该磁场的磁感应强度大小为( )
A. B.
C. D.
10.(多选)如图所示,ABC为竖直平面内的光滑绝缘轨道,其中AB为倾斜直轨道,BC为与AB相切的圆形轨道,并且圆形轨道处在匀强磁场中,磁场方向垂直纸面向里,质量相同的甲、乙、丙三个小球中,甲球带正电,乙球带负电,丙球不带电,现将三个小球在轨道AB上分别从不同高度处由静止释放,都恰好通过圆形轨道的最高点,则( )
A.经过最高点时,三个小球的速度相等
B.经过最高点时,甲球的速度最小
C.甲球的释放位置比乙球的高
D.运动过程中三个小球的机械能均保持不变
11.如图所示,在x轴上方有匀强磁场B,一个质量为m,带电荷量为-q的粒子,以速度v从O点射入磁场,θ角已知,粒子重力不计,求:
(1)粒子在磁场中运动时间为多少?
(2)粒子离开磁场时的位置到O点的距离为多少?
12.如图所示,分布在半径为r的圆形区域内的匀强磁场,磁感应强度为B,方向垂直纸面向里,电荷量为q、质量为m的带正电的粒子从磁场边缘A点沿圆的半径AO方向射入磁场,离开磁场时速度方向偏转了60°角(重力忽略不计)。试确定:
(1)粒子做圆周运动的半径;
(2)粒子的入射速度;
(3)粒子在磁场中运动的时间。
13.如图所示,以MN为界的两匀强磁场,磁感应强度B1=2B2,方向垂直纸面向里,现有一质量为m、带电荷量为q的正粒子,从O点沿图示方向进入B1中。
(1)试画出此粒子的运动轨迹;
(2)求经过多长时间粒子重新回到O点?
1.带电粒子垂直于匀强磁场方向运动时,会受到洛伦兹力的作用。下列表述正确的是( )
A.洛伦兹力对带电粒子做功
B.洛伦兹力不改变带电粒子的动能
C.洛伦兹力的大小与速度无关
D.洛伦兹力不改变带电粒子的速度方向
2.(2015·新课标)两相邻匀强磁场区域的磁感应强度大小不同、方向平行。一速度方向与磁感应强度方向垂直的带电粒子(不计重力),从较强磁场区域进入到较弱磁场区域后,粒子的( )
A.轨道半径减小,角速度增大
B.轨道半径减小,角速度减小
C.轨道半径增大,角速度增大
D.轨道半径增大,角速度减小
3.两个质量相同、所带电荷量相等的带电粒子a、b,以不同的速率对准圆心O沿着AO方向射入圆形匀强磁场区域,其运动轨迹如图。若不计粒子的重力,则下列说法正确的是( )
A.a粒子带正电,b粒子带负电
B.a粒子在磁场中所受洛伦兹力较大
C.b粒子动能较大
D.b粒子在磁场中运动时间较长
4.(多选)如图所示,在圆形区域里,有匀强磁场,方向如图所示。有一束速率各不相同的质子自A点沿半径方向射入磁场,这些质子在磁场中( )
A.运动时间越长的,其轨迹所对应的圆心角越大
B.运动时间越长的,其轨迹越长
C.运动时间越短的射出磁场时,速率越小
D.运动时间越短时,射出磁场时,速度方向偏转越小
5.如右图所示,带负电的粒子以速度v从粒子源P处射出,若图中匀强磁场范围足够大(方向垂直纸面),则带电粒子的可能轨迹是( )
A.a B.b
C.c D.d
6.(多选)如图所示,空间存在水平向右的匀强电场和垂直于纸面向外的匀强磁场。一个带正电的小球套在竖直绝缘细杆上,与细杆间的动摩擦因数为μ,由静止释放后小球将向下运动,设细杆足够长,则( )
A.小球将做匀加速直线运动
B.小球的加速度先增大后减小
C.小球最终将做匀速运动
D.小球将做加速度一直减小的加速运动
7.(多选)如图所示是粒子速度选择器的原理图,如果粒子所具有的速率v = ,那么( )
A.带正电粒子必须沿ab方向从左侧进入场区,才能沿直线通过
B.带负电粒子必须沿ba方向从右侧进入场区,才能沿直线通过
C.不论粒子电性如何,沿ab方向从左侧进入场区,都能沿直线通过
D.不论粒子电性如何,沿ba方向从右侧进入场区,都能沿直线通过
8.长为L的水平板间,有垂直纸面向内的匀强磁场,如图所示,磁感应强度为B,板间距离也为L,板不带电,现有质量为m,电荷量为q的带正电粒子(不计重力),从左边极板间中点处垂直磁感线以速度v水平射入磁场,欲使粒子打在极板上,可采用的办法是( )
A.使粒子的速度v<
B.使粒子的速度v>
C.使粒子的速度v>
D.使粒子的速度
A.E和B都沿水平方向,并与电子运动的方向相同
B.E和B都沿水平方向,并与电子运动的方向相反
C.E竖直向上,B垂直纸面向外
D.E竖直向上,B垂直纸面向里
10.如图所示,带正电的小球用丝线悬挂着,在水平匀强磁场中摆动,摆动平面与磁场垂直,如图所示,图中C点为小球运动的最低点,小球向右运动和向左运动通过C点时,以下说法中正确
的是( )
A.受到的洛伦兹力相同
B.悬线对摆球的拉力相等
C.具有相同的动能
D.具有相同的速度
11.如图所示,质量为m的带正电小球能沿着竖直的绝缘墙竖直下滑,磁感应强度为B的匀强磁场方向水平,并与小球运动方向垂直。若小球带电荷量为q,球与墙间的动摩擦因数为μ,求小球下滑的最大速度和最大加速度。
12.质量为m,电荷量为q的粒子,以初速度v0垂直进入磁感应强度为B、宽度为L的匀强磁场区域,如图所示。求:
(1)带电粒子的运动轨迹及运动性质;
(2)带电粒子运动的轨道半径;
(3)带电粒子离开磁场电的速率;
(4)带电粒子离开磁场时的偏转角θ;
(5)带电粒子在磁场中的运动时间t;
(6)带电粒子离开磁场时偏转的侧位移。
13.如图所示,在x轴的上方(y>0的空间内)存在着垂直于纸面向里、磁感应强度为B的匀强磁场,一个不计重力的带正电粒子从坐标原点O处以速度v进入磁场,粒子进入磁场时的速度方向垂直于磁场且与x轴正方向成45°角,若粒子的质量为m,电荷量为q,求:
(1)该粒子在磁场中做圆周运动的轨道半径;
(2)该粒子在磁场中运动的时间;
(3)该粒子射出磁场的位置坐标。
洛伦兹力
课堂练习
1.B 2.C 3.B 4.AD 5.ABC 6.A 7.D 8.B 9.A 10.CD
11.【答案】(1)t= (2)s=
【解析】(1)粒子做圆周运动的圆心一定在过O点且与速度v垂直的一条直线上,则有 r=,T=,粒子做圆周运动的圆心角(2π-2θ),所用时间t=T=。
(2)粒子离开磁场的位置与入射点的距离即为弦长:s=2rsin θ=。
12.【答案】(1)R=r (2)v= (3)t=
【解析】(1)设粒子做匀速圆周运动的半径为R,如图所示。sin ∠AOD==,所以∠AOD=120°,则三角形ADO′是等边三角形,故R=r。
(2)设洛伦兹力提供向心力:F洛=, 即qvB=,所以v=。
(3)由图知,粒子在磁场中的运动方向偏转了60°角,所以粒子完成了T个圆周运动,根据线速度与周期的关系v=,得T=。 粒子在磁场中的运动时间t=T=。
13.【答案】(1) (2)
【解析】(1)设粒子在磁场B1和B2中做圆周运动的半径为r1、r2,则r1=,r2=,由题意B1=2B2,得r1∶r2=1∶2,根据左手定则判断可以知道,粒子在磁场B1中沿逆时针方向旋转,在磁场B2中沿顺时针方向旋转,则轨迹图如上图。
(2)粒子在磁场B1中运动的时间t1=T1=, 粒子在磁场B2中运动的时间t2=T2=, 则t=t1+t2=。
课后练习
1.B 2.D 3.C 4.AD 5.B 6.BC 7.AC 8.D
9.D 10.C
11.【答案】,g
【解析】小球静止时只受重力,则加速度为g,下滑后,小球受到洛伦兹力、重力、支持力及摩擦力的作用,洛伦兹力水平向左,摩擦力竖直向上,小球向下做加速运动,速度越大,洛伦兹力越大,则摩擦力越大,加速度越小,当加速度等于零时,速度最大,则mg=μqvB,得v=。 此后小球做匀速直线运动,加速度为0,故开始时小球的加速度最大:a=g。
12.【答案】(1)见解析 (2) (2)v0
(3)arcsin (5) (6)(1-cos θ)
【解析】(1)粒子在磁场中受到洛伦兹力作用,力与速度始终垂直,故粒子做匀速圆周运动,轨迹是圆周。如图:
(2)由qv0B=m 得R=。
(3)粒子在磁场中只受到洛伦兹力作用,只改变速度方向,不改变大小,故离开磁场时速率仍为初速度大小v0。
(4)由几何关系可知:sin θ==。
(5)在磁场中的运动时间t==。
(6)y=R(1-cos θ)=(1-cos θ)。
13.【答案】(1) (2) (3)
【解析】(1)设粒子在磁场中做圆周运动的半径为R,由洛伦兹力和牛顿第二定律,有:qvB=,所以R=。
(2)粒子在磁场中运动对应的圆心角为270°, 又T=,所以t=T=。
(3)粒子离开磁场的位置,由几何关系得x=R,又R=,所以x=。 所以粒子射出磁场的位置坐标为。
