黑龙江省双鸭山市重点中学2020-2021学年高二下学期开学考试数学(理)试卷 Word版含答案
文档属性
| 名称 | 黑龙江省双鸭山市重点中学2020-2021学年高二下学期开学考试数学(理)试卷 Word版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-15 00:00:00 | ||
图片预览



文档简介
高二 数学(理科)
(考试时间:120分钟 总分:150分)
第Ⅰ卷(12题:共60分)
一、选择题(包括12小题,每小题5分,共60分)
1.为响应国家“节约粮食”的号召,某同学决定在某食堂提供的2种主食、3种素菜、2种大荤、4种小荤中选取一种主食、一种素菜、一种荤菜作为今日伙食,并在用餐时积极践行“光盘行动”,则不同的选取方法有( )
A.48种 B.36种 C.24种 D.12种
2.某工厂为了对40个零件进行抽样调查,将其编号为00,01,…38,39.现要从中选出5个,利用下面的随机数表,从第一行第3列开始,由左至右依次读取,选出来的第5个零件编号是( )
0647 4373 8636 9647 3661 4698 6371 6233 2616 8045 6011 1410
9577 7424 6762 4281 1457 2042 5332 3732 2707 3607 5124 5179
A.36 B.16 C.11 D.14
3.将十进制数19转化为二进制数为( )
A. B. C. D.
4.某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则的值是( )
A.10 B.11
C.12 D.13
5.2021年是中国共产党建党100周年.某校为了纪念党的生日,计划举办大型文艺汇演,某班选择合唱《没有共产党就没有新中国》这首歌.仅从逻辑学角度来看,“没有共产党就没有新中国”这句歌词中体现了“有共产党”是“有新中国”的( )
A.充分条件 B.必要条件
C.充要条件 D.既不充分也不必要条件
6.下列命题正确的有( )
①用相关指数来刻画回归效果,越小,说明模型的拟合效果越好;
②若一组数据8,12,x,11,9的平均数是10,则其方差是2;
③回归直线一定过样本点的中心();
④若相关系数,则两个变量之间线性关系性强.
A.1个 B.2个 C.3个 D.4个
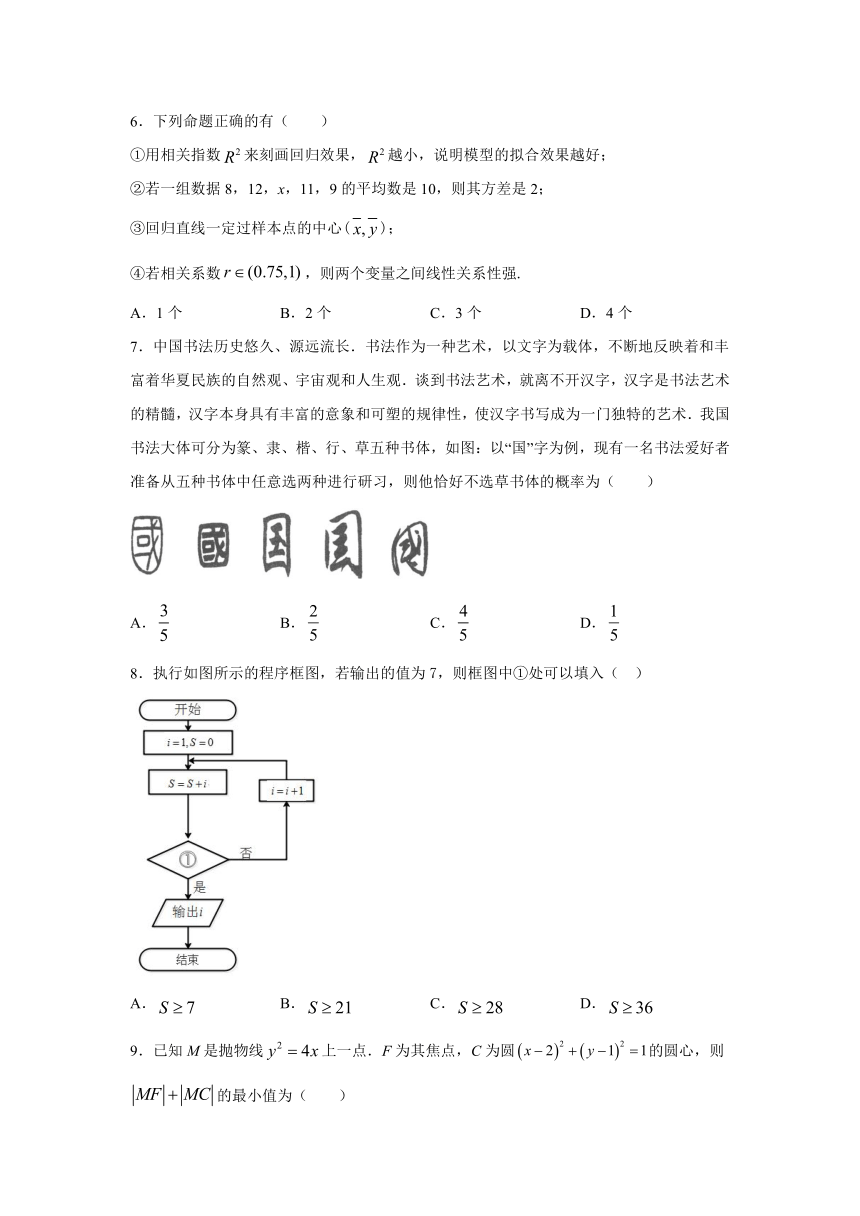
7.中国书法历史悠久、源远流长.书法作为一种艺术,以文字为载体,不断地反映着和丰富着华夏民族的自然观、宇宙观和人生观.谈到书法艺术,就离不开汉字,汉字是书法艺术的精髓,汉字本身具有丰富的意象和可塑的规律性,使汉字书写成为一门独特的艺术.我国书法大体可分为篆、隶、楷、行、草五种书体,如图:以“国”字为例,现有一名书法爱好者准备从五种书体中任意选两种进行研习,则他恰好不选草书体的概率为( )
A. B. C. D.
8.执行如图所示的程序框图,若输出的值为7,则框图中①处可以填入( )
A. B. C. D.
9.已知M是抛物线上一点.F为其焦点,C为圆的圆心,则的最小值为( )
A.2 B.3 C.4 D.5
10.某中学早上8点开始上课,若学生小明与小方均在早上7:40至8:00之间到校,且两人在该时间段的任何时刻到校都是等可能的,则小明比小方至少早5分钟到校的概率为( )
A. B. C. D.
11.在棱长为的正方体中,分别为棱、的中点,为棱上的一点,且,则点到平面的距离为( )
A. B. C. D.
12.已知椭圆的焦点为,,是椭圆上一点,且,若的内切圆的半径满足,则椭圆的离心率为( )
A. B. C. D.
第Ⅱ卷(10题:共90分)
二、填空题(包括4小题,每小题5分,共20分)
13.如图,在正方体中,上底面中心为,则异面直线与所成角的余弦值为______
14.位同学其中男生女生排成一排照相,男生不相邻的排法有___________种
15.已知为双曲线的左焦点,为上的点.若的长等于虚轴长的2倍,点在线段上,则的周长为__________.
16.验证码就是将一串随机产生的数字或符号,生成一幅图片,图片里加上一些干扰象素(防止),由用户肉眼识别其中的验证码信息,输入表单提交网站验证,验证成功后才能使用某项功能.很多网站利用验证码技术来防止恶意登录,以提升网络安全.在抗疫期间,某居民小区电子出入证的登录验证码由0,1,2,…,9中的五个数字随机组成.将中间数字最大,然后向两边对称递减的验证码称为“钟型验证码”(例如:如14532,12543),已知某人收到了一个“钟型验证码”,则该验证码的中间数字是7的概率为__________.
三、解答题(包括6小题,共70分)
17.(10分)有四个编有1?2?3?4的四个不同的盒子,有编有1?2?3?4的四个不同的小球,现把四个小球逐个随机放入四个盒子里.
(1)小球全部放入盒子中有多少种不同的放法?
(2)在(1)的条件下求恰有一个盒子没放球的概率?
(3)若没有一个盒子空着,但球的编号与盒子编号不全相同,有多少种投放方法?
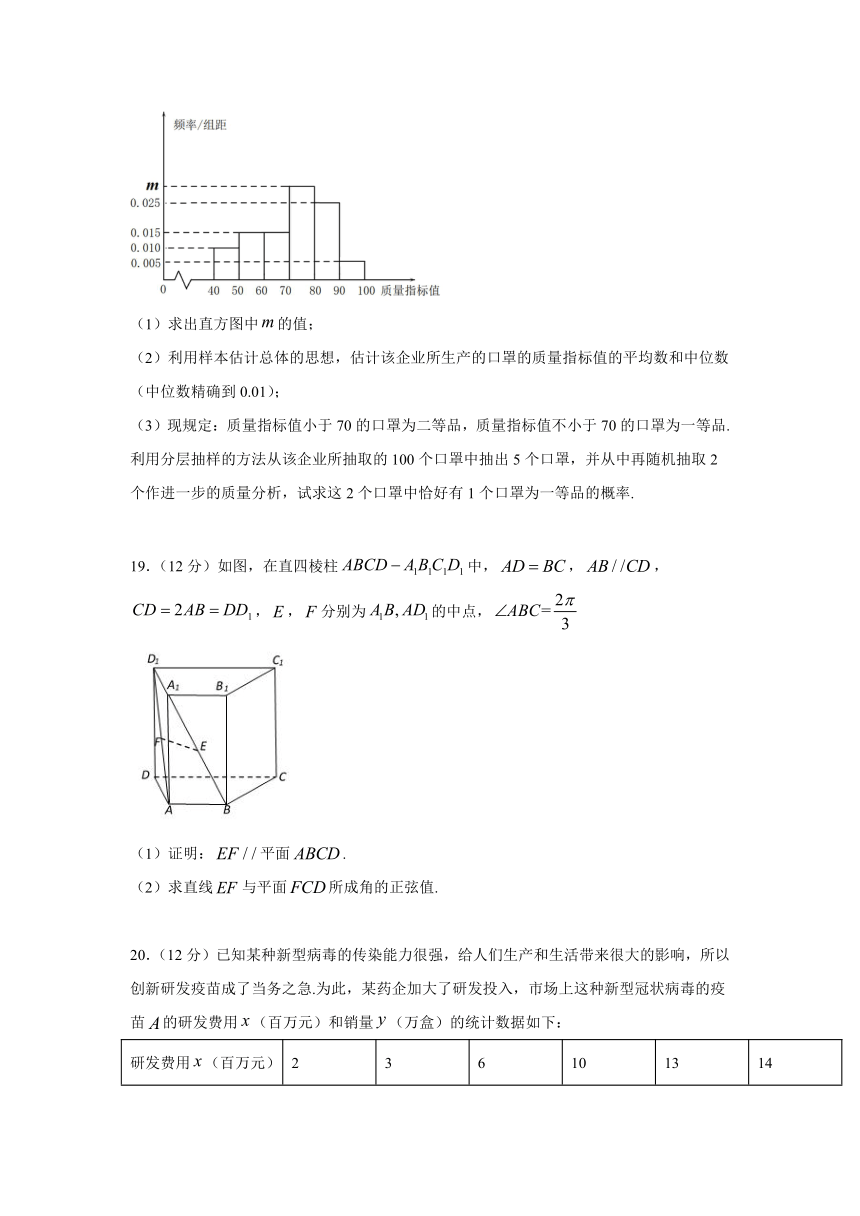
18.(12分)在全球抗击新冠肺炎疫情期间,我国医疗物资生产企业加班加点生产口罩、防护服、消毒水等防疫物品,保障抗疫一线医疗物资供应,在国际社会上赢得一片赞誉.我国某口罩生产企业在加大生产的同时,狠抓质量管理,不定时抽查口罩质量,该企业质检人员从所生产的口罩中随机抽取了100个,将其质量指标值分成以下六组:,,,…,,得到如下频率分布直方图.
(1)求出直方图中的值;
(2)利用样本估计总体的思想,估计该企业所生产的口罩的质量指标值的平均数和中位数(中位数精确到0.01);
(3)现规定:质量指标值小于70的口罩为二等品,质量指标值不小于70的口罩为一等品.利用分层抽样的方法从该企业所抽取的100个口罩中抽出5个口罩,并从中再随机抽取2个作进一步的质量分析,试求这2个口罩中恰好有1个口罩为一等品的概率.
19.(12分)如图,在直四棱柱中,,,,,分别为的中点,
(1)证明:平面.
(2)求直线与平面所成角的正弦值.
20.(12分)已知某种新型病毒的传染能力很强,给人们生产和生活带来很大的影响,所以创新研发疫苗成了当务之急.为此,某药企加大了研发投入,市场上这种新型冠状病毒的疫苗的研发费用(百万元)和销量(万盒)的统计数据如下:
研发费用(百万元) 2 3 6 10 13 14
销量(万盒) 1 1 2 2.5 4 4.5
(1)根据上表中的数据,建立关于的线性回归方程(用分数表示);
(2)根据所求的回归方程,估计当研发费用为1600万元时,销售量为多少?
参考公式:,.
21.(12分)在三棱柱中,侧面,,,.
(1)求证:;
(2)若E为棱的中点,且与平面所成角的正弦值为,求二面角的大小.
22.(12分)已知椭圆:过点且离心率为.
(1)求椭圆的标准方程;
(2)若,分别为的左右顶点,为直线上的任意一点,直线,分别与相交于、两点,连接,试证明直线过定点,并求出该定点的坐标.
答案
1.B
解:由题意可知,分三步完成:
第一步,从2种主食中任选一种有2种选法;
第二步,从3种素菜中任选一种有3种选法;
第三步,从6种荤菜中任选一种有6种选法,
根据分步计数原理,共有不同的选取方法,
2.C
利用随机数表,从第一行第3列开始,由左至由一次读取,
即47开始读取,在编号范围内的提取出来,可得,
则选出来的第5个零件编号是.
3.C
19÷2=9…1,9÷2=4…1,4÷2=2…0,2÷2=1…0,1÷2=0…1,故19(10)=10011(2).
4.C
试题分析::∵甲组学生成绩的平均数是88,
∴由茎叶图可知78+86+84+88+95+90+m+92=88×7,∴m=3
又乙组学生成绩的中位数是89,∴n=9,
∴m+n=12
5.B
命题:“没有共产党就没有新中国”,即是“如果没有共产党,那么就没有新中国”;
其逆否命题为“如果有新中国,那么就有共产党”;
即根据“有新中国”能推出“有共产党”,所以“有共产党”是“有新中国”的必要条件.
6.C
用相关指数来刻画回归效果,越大,说明模型的拟合效果越好;所以①错误;
若一组数据8,12,x,11,9的平均数是10,则,其方差是,所以②正确;
回归直线方程一定过样本点的中心(),所以③正确;
因为相关系数越大,两个变量之间线性关系性越强,因此若相关系数,则两个变量之间线性关系性强.即④正确
7.A
从五种书体中任意选两种进行研习,共有种,则不选草书体共有种,
则不选草书体的概率为.
8.C
第一次循环:,不满足条件,;
第二次循环:,不满足条件,;
第三次循环:,不满足条件,;
第四次循环:,不满足条件,;
第五次循环:,不满足条件,;
第六次循环:,不满足条件,;
第七次循环:,满足条件,输出的值为7.
所以判断框中的条件可填写“”.
9.B
作垂直准线,垂足为,根据抛物线的定义有,,当且仅当在同一直线上时取等号,此时取得最小值,最小值为3.
10.D
设小明到校时间为,小方到校时间为
可以看成平面中的点试验的全部结果所构成的区域为
是一个矩形区域,
对应的面积
则小明比小方至少早分钟到校事件,作出符合题意的图象
则符合题意得区域为,联立
,得,由,得
则,由几何概率模型可知小明比小方至少早分钟到校的概率为
.
11.D
以为原点,为轴、为轴、为轴,建立空间直角坐标系,
则,
,
设平面的法向量,
则,取,得,
点到平面的距离为
.
12.C
由题可知,
即,
在中,利用椭圆定义知,由余弦定理得
即,整理得
易得面积
又的内切圆的半径为,利用等面积法可知,
所以
由已知,得,则,即
在中,利用正弦定理知
即,又,整理得
两边同除以,则,解得或(舍去)
13.
由题意,连接和,设正方体的棱长为,则,
在正方体中,可得,
所以异面直线与所成角即为直线与所成角,设,
在直角中,可得
在直角中,可得.
14.
先将名女生排序,然后将名男生插入名女生所形成的空位中,
所以,男生不相邻的排法种数为.
15.40
由双曲线方程得,则虚轴长为6,线段过点为双曲线的右焦点,,,的周长为
16.
根据“钟型验证码” 中间数字最大,然后向两边对称递减,所以中间的数字可能是.
当中间是时,其它个数字可以是,选其中两个排在左边(排法唯一),另外两个排在右边(排法唯一),所以方法数有种.
当中间是时,其它个数字可以是,选其中两个排在左边(排法唯一),另外两个排在右边(排法唯一),所以方法数有种.
当中间是时,其它个数字可以是,选其中两个排在左边(排法唯一),另外两个排在右边(排法唯一),所以方法数有种.
当中间是时,其它个数字可以是,选其中两个排在左边(排法唯一),另外两个排在右边(排法唯一),所以方法数有种.
当中间是时,其它个数字可以是,选其中两个排在左边(排法唯一),另外两个排在右边(排法唯一),所以方法数有种.
当中间是时,其它个数字可以是,选其中两个排在左边(排法唯一),另外两个排在右边(排法唯一),所以方法数有种.
所以该验证码的中间数字是7的概率为.
17.(1)种;(2);(3)种.
(1)每个球都有4种方法,故有种
(2)从4个小球中选两个作为一个元素,同另外两个元素在三个位置全排列,故共有种不同的放法.概率为:
(3)每个盒子不空,共有,种.
18.(1)(2)平均数为71,中位数为73.33(3)
(1)由,
得.
(2)平均数为,
设中位数为,
则,得.
故可以估计该企业所生产口罩的质量指标值的平均数为71,中位数为73.33.
(3)由频率分布直方图可知:100个口罩中一等品、二等品各有60个、40个,
由分层抽样可知,所抽取的5个口罩中一等品、二等品各有3个、2个.
记这3个一等品为,,,2个二等品为,,则从5个口罩中抽取2个的可能结果有:,,,,,,,,,,共10种,
其中恰有1个口罩为一等品的可能结果有:,,,,,.共6种.
故这2个口罩中恰好有1个口罩为一等品的概率为.
19.(1)证明见解析;(2).
解:(1)连接,,易知侧面为矩形,
为的中点,为的中点.
为的中点,
平面,平面
平面
(2)在平面中,过点作,易知平面,
故以为原点,分别以所在直
线为轴建立如图所示空间直角坐标系,
设,
则,,
, ,
,,
设平面的法向量为,
由 即 , 解得
令 得,所以
所以直线与平面所成角的正弦值为.
20.(1);(2)销售量为47769盒.
(1),,
,,,
,
(2)当时,代入回归方程(万盒)(盒)
当研发费用为16000000时,销售量为47769盒.
21.(1)证明见详解;(2).
解:(1)三角形中,,,,
利用余弦定理可得,,即,
故,又侧面,建立如图空间直角坐标系,设,.
则,,,,
则,故,
所以,即;
(2)由,,且相交于平面内,故平面,即是平面的法向量,由E为棱的中点知,,
因为与平面所成角的正弦值为,则,
故,解得,
则,,,
设平面法向量为,由得,即,
设平面的法向量为,由得,即 ,
则,又由图可知二面角是锐二面角,
故二面角的大小为.
22.(1);(2)证明见解析;定点(4,0).
(1)由题可知,,解得:,,,
椭圆的标准程为:;
(2)由题知有斜率,设直线方程为,,,
联立椭圆得,
,
设,∵、、三点共线,,∴,
同理、、三点共线,,∴,
∴,两式相除得:
,
化简得,即,
,解得或
当时,直线的方程为,恒过点(1,0),当点不在轴时,,故不满足,舍去;
当时,直线的方程为,恒过点(4,0),符合题意,
综上,直线恒过定点.
(考试时间:120分钟 总分:150分)
第Ⅰ卷(12题:共60分)
一、选择题(包括12小题,每小题5分,共60分)
1.为响应国家“节约粮食”的号召,某同学决定在某食堂提供的2种主食、3种素菜、2种大荤、4种小荤中选取一种主食、一种素菜、一种荤菜作为今日伙食,并在用餐时积极践行“光盘行动”,则不同的选取方法有( )
A.48种 B.36种 C.24种 D.12种
2.某工厂为了对40个零件进行抽样调查,将其编号为00,01,…38,39.现要从中选出5个,利用下面的随机数表,从第一行第3列开始,由左至右依次读取,选出来的第5个零件编号是( )
0647 4373 8636 9647 3661 4698 6371 6233 2616 8045 6011 1410
9577 7424 6762 4281 1457 2042 5332 3732 2707 3607 5124 5179
A.36 B.16 C.11 D.14
3.将十进制数19转化为二进制数为( )
A. B. C. D.
4.某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则的值是( )
A.10 B.11
C.12 D.13
5.2021年是中国共产党建党100周年.某校为了纪念党的生日,计划举办大型文艺汇演,某班选择合唱《没有共产党就没有新中国》这首歌.仅从逻辑学角度来看,“没有共产党就没有新中国”这句歌词中体现了“有共产党”是“有新中国”的( )
A.充分条件 B.必要条件
C.充要条件 D.既不充分也不必要条件
6.下列命题正确的有( )
①用相关指数来刻画回归效果,越小,说明模型的拟合效果越好;
②若一组数据8,12,x,11,9的平均数是10,则其方差是2;
③回归直线一定过样本点的中心();
④若相关系数,则两个变量之间线性关系性强.
A.1个 B.2个 C.3个 D.4个
7.中国书法历史悠久、源远流长.书法作为一种艺术,以文字为载体,不断地反映着和丰富着华夏民族的自然观、宇宙观和人生观.谈到书法艺术,就离不开汉字,汉字是书法艺术的精髓,汉字本身具有丰富的意象和可塑的规律性,使汉字书写成为一门独特的艺术.我国书法大体可分为篆、隶、楷、行、草五种书体,如图:以“国”字为例,现有一名书法爱好者准备从五种书体中任意选两种进行研习,则他恰好不选草书体的概率为( )
A. B. C. D.
8.执行如图所示的程序框图,若输出的值为7,则框图中①处可以填入( )
A. B. C. D.
9.已知M是抛物线上一点.F为其焦点,C为圆的圆心,则的最小值为( )
A.2 B.3 C.4 D.5
10.某中学早上8点开始上课,若学生小明与小方均在早上7:40至8:00之间到校,且两人在该时间段的任何时刻到校都是等可能的,则小明比小方至少早5分钟到校的概率为( )
A. B. C. D.
11.在棱长为的正方体中,分别为棱、的中点,为棱上的一点,且,则点到平面的距离为( )
A. B. C. D.
12.已知椭圆的焦点为,,是椭圆上一点,且,若的内切圆的半径满足,则椭圆的离心率为( )
A. B. C. D.
第Ⅱ卷(10题:共90分)
二、填空题(包括4小题,每小题5分,共20分)
13.如图,在正方体中,上底面中心为,则异面直线与所成角的余弦值为______
14.位同学其中男生女生排成一排照相,男生不相邻的排法有___________种
15.已知为双曲线的左焦点,为上的点.若的长等于虚轴长的2倍,点在线段上,则的周长为__________.
16.验证码就是将一串随机产生的数字或符号,生成一幅图片,图片里加上一些干扰象素(防止),由用户肉眼识别其中的验证码信息,输入表单提交网站验证,验证成功后才能使用某项功能.很多网站利用验证码技术来防止恶意登录,以提升网络安全.在抗疫期间,某居民小区电子出入证的登录验证码由0,1,2,…,9中的五个数字随机组成.将中间数字最大,然后向两边对称递减的验证码称为“钟型验证码”(例如:如14532,12543),已知某人收到了一个“钟型验证码”,则该验证码的中间数字是7的概率为__________.
三、解答题(包括6小题,共70分)
17.(10分)有四个编有1?2?3?4的四个不同的盒子,有编有1?2?3?4的四个不同的小球,现把四个小球逐个随机放入四个盒子里.
(1)小球全部放入盒子中有多少种不同的放法?
(2)在(1)的条件下求恰有一个盒子没放球的概率?
(3)若没有一个盒子空着,但球的编号与盒子编号不全相同,有多少种投放方法?
18.(12分)在全球抗击新冠肺炎疫情期间,我国医疗物资生产企业加班加点生产口罩、防护服、消毒水等防疫物品,保障抗疫一线医疗物资供应,在国际社会上赢得一片赞誉.我国某口罩生产企业在加大生产的同时,狠抓质量管理,不定时抽查口罩质量,该企业质检人员从所生产的口罩中随机抽取了100个,将其质量指标值分成以下六组:,,,…,,得到如下频率分布直方图.
(1)求出直方图中的值;
(2)利用样本估计总体的思想,估计该企业所生产的口罩的质量指标值的平均数和中位数(中位数精确到0.01);
(3)现规定:质量指标值小于70的口罩为二等品,质量指标值不小于70的口罩为一等品.利用分层抽样的方法从该企业所抽取的100个口罩中抽出5个口罩,并从中再随机抽取2个作进一步的质量分析,试求这2个口罩中恰好有1个口罩为一等品的概率.
19.(12分)如图,在直四棱柱中,,,,,分别为的中点,
(1)证明:平面.
(2)求直线与平面所成角的正弦值.
20.(12分)已知某种新型病毒的传染能力很强,给人们生产和生活带来很大的影响,所以创新研发疫苗成了当务之急.为此,某药企加大了研发投入,市场上这种新型冠状病毒的疫苗的研发费用(百万元)和销量(万盒)的统计数据如下:
研发费用(百万元) 2 3 6 10 13 14
销量(万盒) 1 1 2 2.5 4 4.5
(1)根据上表中的数据,建立关于的线性回归方程(用分数表示);
(2)根据所求的回归方程,估计当研发费用为1600万元时,销售量为多少?
参考公式:,.
21.(12分)在三棱柱中,侧面,,,.
(1)求证:;
(2)若E为棱的中点,且与平面所成角的正弦值为,求二面角的大小.
22.(12分)已知椭圆:过点且离心率为.
(1)求椭圆的标准方程;
(2)若,分别为的左右顶点,为直线上的任意一点,直线,分别与相交于、两点,连接,试证明直线过定点,并求出该定点的坐标.
答案
1.B
解:由题意可知,分三步完成:
第一步,从2种主食中任选一种有2种选法;
第二步,从3种素菜中任选一种有3种选法;
第三步,从6种荤菜中任选一种有6种选法,
根据分步计数原理,共有不同的选取方法,
2.C
利用随机数表,从第一行第3列开始,由左至由一次读取,
即47开始读取,在编号范围内的提取出来,可得,
则选出来的第5个零件编号是.
3.C
19÷2=9…1,9÷2=4…1,4÷2=2…0,2÷2=1…0,1÷2=0…1,故19(10)=10011(2).
4.C
试题分析::∵甲组学生成绩的平均数是88,
∴由茎叶图可知78+86+84+88+95+90+m+92=88×7,∴m=3
又乙组学生成绩的中位数是89,∴n=9,
∴m+n=12
5.B
命题:“没有共产党就没有新中国”,即是“如果没有共产党,那么就没有新中国”;
其逆否命题为“如果有新中国,那么就有共产党”;
即根据“有新中国”能推出“有共产党”,所以“有共产党”是“有新中国”的必要条件.
6.C
用相关指数来刻画回归效果,越大,说明模型的拟合效果越好;所以①错误;
若一组数据8,12,x,11,9的平均数是10,则,其方差是,所以②正确;
回归直线方程一定过样本点的中心(),所以③正确;
因为相关系数越大,两个变量之间线性关系性越强,因此若相关系数,则两个变量之间线性关系性强.即④正确
7.A
从五种书体中任意选两种进行研习,共有种,则不选草书体共有种,
则不选草书体的概率为.
8.C
第一次循环:,不满足条件,;
第二次循环:,不满足条件,;
第三次循环:,不满足条件,;
第四次循环:,不满足条件,;
第五次循环:,不满足条件,;
第六次循环:,不满足条件,;
第七次循环:,满足条件,输出的值为7.
所以判断框中的条件可填写“”.
9.B
作垂直准线,垂足为,根据抛物线的定义有,,当且仅当在同一直线上时取等号,此时取得最小值,最小值为3.
10.D
设小明到校时间为,小方到校时间为
可以看成平面中的点试验的全部结果所构成的区域为
是一个矩形区域,
对应的面积
则小明比小方至少早分钟到校事件,作出符合题意的图象
则符合题意得区域为,联立
,得,由,得
则,由几何概率模型可知小明比小方至少早分钟到校的概率为
.
11.D
以为原点,为轴、为轴、为轴,建立空间直角坐标系,
则,
,
设平面的法向量,
则,取,得,
点到平面的距离为
.
12.C
由题可知,
即,
在中,利用椭圆定义知,由余弦定理得
即,整理得
易得面积
又的内切圆的半径为,利用等面积法可知,
所以
由已知,得,则,即
在中,利用正弦定理知
即,又,整理得
两边同除以,则,解得或(舍去)
13.
由题意,连接和,设正方体的棱长为,则,
在正方体中,可得,
所以异面直线与所成角即为直线与所成角,设,
在直角中,可得
在直角中,可得.
14.
先将名女生排序,然后将名男生插入名女生所形成的空位中,
所以,男生不相邻的排法种数为.
15.40
由双曲线方程得,则虚轴长为6,线段过点为双曲线的右焦点,,,的周长为
16.
根据“钟型验证码” 中间数字最大,然后向两边对称递减,所以中间的数字可能是.
当中间是时,其它个数字可以是,选其中两个排在左边(排法唯一),另外两个排在右边(排法唯一),所以方法数有种.
当中间是时,其它个数字可以是,选其中两个排在左边(排法唯一),另外两个排在右边(排法唯一),所以方法数有种.
当中间是时,其它个数字可以是,选其中两个排在左边(排法唯一),另外两个排在右边(排法唯一),所以方法数有种.
当中间是时,其它个数字可以是,选其中两个排在左边(排法唯一),另外两个排在右边(排法唯一),所以方法数有种.
当中间是时,其它个数字可以是,选其中两个排在左边(排法唯一),另外两个排在右边(排法唯一),所以方法数有种.
当中间是时,其它个数字可以是,选其中两个排在左边(排法唯一),另外两个排在右边(排法唯一),所以方法数有种.
所以该验证码的中间数字是7的概率为.
17.(1)种;(2);(3)种.
(1)每个球都有4种方法,故有种
(2)从4个小球中选两个作为一个元素,同另外两个元素在三个位置全排列,故共有种不同的放法.概率为:
(3)每个盒子不空,共有,种.
18.(1)(2)平均数为71,中位数为73.33(3)
(1)由,
得.
(2)平均数为,
设中位数为,
则,得.
故可以估计该企业所生产口罩的质量指标值的平均数为71,中位数为73.33.
(3)由频率分布直方图可知:100个口罩中一等品、二等品各有60个、40个,
由分层抽样可知,所抽取的5个口罩中一等品、二等品各有3个、2个.
记这3个一等品为,,,2个二等品为,,则从5个口罩中抽取2个的可能结果有:,,,,,,,,,,共10种,
其中恰有1个口罩为一等品的可能结果有:,,,,,.共6种.
故这2个口罩中恰好有1个口罩为一等品的概率为.
19.(1)证明见解析;(2).
解:(1)连接,,易知侧面为矩形,
为的中点,为的中点.
为的中点,
平面,平面
平面
(2)在平面中,过点作,易知平面,
故以为原点,分别以所在直
线为轴建立如图所示空间直角坐标系,
设,
则,,
, ,
,,
设平面的法向量为,
由 即 , 解得
令 得,所以
所以直线与平面所成角的正弦值为.
20.(1);(2)销售量为47769盒.
(1),,
,,,
,
(2)当时,代入回归方程(万盒)(盒)
当研发费用为16000000时,销售量为47769盒.
21.(1)证明见详解;(2).
解:(1)三角形中,,,,
利用余弦定理可得,,即,
故,又侧面,建立如图空间直角坐标系,设,.
则,,,,
则,故,
所以,即;
(2)由,,且相交于平面内,故平面,即是平面的法向量,由E为棱的中点知,,
因为与平面所成角的正弦值为,则,
故,解得,
则,,,
设平面法向量为,由得,即,
设平面的法向量为,由得,即 ,
则,又由图可知二面角是锐二面角,
故二面角的大小为.
22.(1);(2)证明见解析;定点(4,0).
(1)由题可知,,解得:,,,
椭圆的标准程为:;
(2)由题知有斜率,设直线方程为,,,
联立椭圆得,
,
设,∵、、三点共线,,∴,
同理、、三点共线,,∴,
∴,两式相除得:
,
化简得,即,
,解得或
当时,直线的方程为,恒过点(1,0),当点不在轴时,,故不满足,舍去;
当时,直线的方程为,恒过点(4,0),符合题意,
综上,直线恒过定点.
同课章节目录
